Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Menal, Pera
and
Vaserstein, Leonid N.
1989.
On subgroups ofGL 2 over non-commutative local rings which are normalized by elementary matrices.
Mathematische Annalen,
Vol. 285,
Issue. 2,
p.
221.
Mason, A. W.
1989.
OnGL2of a local ring in which 2 is not a unit II.
Communications in Algebra,
Vol. 17,
Issue. 3,
p.
511.
Menal, Pere
and
Vaserstein, Leonid N.
1990.
On the structure of GL2 over stable range one rings.
Journal of Pure and Applied Algebra,
Vol. 64,
Issue. 2,
p.
149.
Menal, Pere
and
Vaserstein, Leonid N.
1991.
On subgroups of GL2 over Banach algebras and von Neumann regular rings which are normalized by elementary matrices.
Journal of Algebra,
Vol. 138,
Issue. 1,
p.
99.
Mason, A. W.
1991.
The order and level of a subgroup of GL2 over a Dedekind ring of arithmetic type.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 119,
Issue. 3-4,
p.
191.
Mason, A.W.
1992.
Normal subgroups of SL2(k[t]) with or without free quotients.
Journal of Algebra,
Vol. 150,
Issue. 2,
p.
281.
Mason, A.W.
1993.
Congruence hulls in SLn.
Journal of Pure and Applied Algebra,
Vol. 89,
Issue. 3,
p.
255.
Vavilov, N. A.
and
Stepanov, A. V.
2013.
Linear groups over general rings. I. Generalities.
Journal of Mathematical Sciences,
Vol. 188,
Issue. 5,
p.
490.
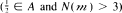 . Results of Lacroix show that this is also true when n = 2 and N(m) = 3, provided that N∩2(A) ≠ SL2(A)'.
. Results of Lacroix show that this is also true when n = 2 and N(m) = 3, provided that N∩2(A) ≠ SL2(A)'.