Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fukagai, Nobuyoshi
and
Kusano, Taka?i
1983.
On second order functional differential equations and inequalities with deviating arguments.
Monatshefte f�r Mathematik,
Vol. 96,
Issue. 2,
p.
107.
Grace, S.R
and
Lalli, B.S
1984.
Oscillatory and asymptotic behavior of solutions of differential equations with deviating arguments.
Journal of Mathematical Analysis and Applications,
Vol. 104,
Issue. 1,
p.
79.
Ladas, G.
Sficas, Y. G.
and
Stavroulakis, I. P.
1984.
Necessary and sufficient conditions for oscillations of higher order delay differential equations.
Transactions of the American Mathematical Society,
Vol. 285,
Issue. 1,
p.
81.
Ladas, G.
Sficas, Y.G.
and
Stavroulakis, I.P.
1984.
Differential Equations, Proceedings of the Conference held at The University of Alabama in Birmingham.
Vol. 92,
Issue. ,
p.
373.
Georgiou, D
and
Kreith, K
1985.
Functional characteristic initial value problems.
Journal of Mathematical Analysis and Applications,
Vol. 107,
Issue. 2,
p.
414.
Kreith, K.
and
Ladas, G.
1985.
Allowable delays for positive diffusion processes.
Hiroshima Mathematical Journal,
Vol. 15,
Issue. 2,
Grace, S.R
and
Lalli, B.S
1985.
Oscillation theorems for certain delay differential inequalities.
Journal of Mathematical Analysis and Applications,
Vol. 106,
Issue. 2,
p.
414.
Zhang, B.G.
1985.
Trends in The Theory and Practice of Non-Linear Analysis, Proceedings of the VIth International Conference on Trends in the Theory and Practice of Non-Linear Analysis.
Vol. 110,
Issue. ,
p.
475.
Ladas, G.
and
Sficas, Y. G.
1986.
Oscilations of higher-order neutral equations.
The Journal of the Australian Mathematical Society. Series B. Applied Mathematics,
Vol. 27,
Issue. 4,
p.
502.
Werbowski, Jaroslaw
1987.
Oscillations of differential inequalities caused by several delay arguments.
Journal of Mathematical Analysis and Applications,
Vol. 124,
Issue. 1,
p.
200.
Grammatikopoulos, M. K.
Ladas, G.
and
Meimaridou, A.
1987.
Oscillation and asymptotic behavior of second order neutral differential equations.
Annali di Matematica Pura ed Applicata,
Vol. 148,
Issue. 1,
p.
29.
Wang, Zhicheng
1989.
A necessary and sufficient condition for the oscillation of higher-order neutral equations.
Tohoku Mathematical Journal,
Vol. 41,
Issue. 4,
Wudu, Lu
1990.
The asymptotic and oscillatory behavior of the solutions of higher order neutral equations.
Journal of Mathematical Analysis and Applications,
Vol. 148,
Issue. 2,
p.
378.
Chuanxi, Q.
and
Ladas, G.
1991.
Oscillations of Higher Order Neutral Differential Equations with Variable Coefficients.
Mathematische Nachrichten,
Vol. 150,
Issue. 1,
p.
15.
Bilchev, S. J.
Grammatikopoulos, M. K.
and
Stavroulakis, I. P.
1992.
Oscillations of higher order neutral differential equations.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 52,
Issue. 2,
p.
261.
Grace, S.R.
1995.
Oscillations of mixed neutral functional differential equations.
Applied Mathematics and Computation,
Vol. 68,
Issue. 1,
p.
1.
Grace, S. R.
1999.
Oscillations of certain functional differential equations.
Czechoslovak Mathematical Journal,
Vol. 49,
Issue. 1,
p.
45.
Youshan, Tao
and
Guozhu, Gao
2001.
Oscillation for forced odd order neutral differential equations.
Applied Mathematics-A Journal of Chinese Universities,
Vol. 16,
Issue. 2,
p.
133.
Candan, T.
and
Dahiya, R.S.
2008.
On the oscillation of certain mixed neutral equations.
Applied Mathematics Letters,
Vol. 21,
Issue. 3,
p.
222.
Candan, T.
and
Dahiya, R. S.
2008.
Oscillation of mixed neutral functional differential equations with distributed deviating arguments.
Differential Equations and Dynamical Systems,
Vol. 16,
Issue. 3,
p.
207.
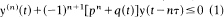 and
and 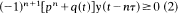 and the delay differential equation
and the delay differential equation 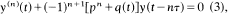 , where q(t) ≥ 0 is a continuous function and p, τ are positive constants. Under the condition pτe ≥ 1 we prove that when n is odd (1) has no eventually positive solutions, (2) has no eventually negative solutions, and (3) has only oscillatory solutions and when n is even (1) has no eventually negative bounded solutions, (2) has no eventually positive bounded solutions, and every bounded solution of (3) is oscillatory. The condition pτe > 1 is sharp. The above results, which generalize previous results by Ladas and by Ladas and Stavroulakis for first order delay differential inequalities, are caused by the retarded argument and do not hold when τ = 0.
, where q(t) ≥ 0 is a continuous function and p, τ are positive constants. Under the condition pτe ≥ 1 we prove that when n is odd (1) has no eventually positive solutions, (2) has no eventually negative solutions, and (3) has only oscillatory solutions and when n is even (1) has no eventually negative bounded solutions, (2) has no eventually positive bounded solutions, and every bounded solution of (3) is oscillatory. The condition pτe > 1 is sharp. The above results, which generalize previous results by Ladas and by Ladas and Stavroulakis for first order delay differential inequalities, are caused by the retarded argument and do not hold when τ = 0.