Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T12:27:56.737Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Lemma of M. Abramson

Published online by Cambridge University Press:  20 November 2018

C.A. Church Jr.
C.A. Church Jr.*
Affiliation:
West Virginia University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Kaplansky's Lemma [3] states: the number of k-combinations of 1, 2,…, n with no two consecutive integers in any selection is 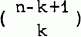Using this, Abramson [l; lemma 3] solves the problem: find the, number of k-combinations so that no two integers i and i+2 appear in any selection. (This is generalized by Abramson in [2].) An interesting solution, also using Kaplansky's lemma, is obtained as follows.

If n = 2m, we choose s from among the m even integer s, no two consecutive, and k- s from among the m odd integers, no two consecutive.

Type
Notes and Problems
Information
Canadian Mathematical Bulletin , Volume 9 , Issue 3 , August 1966 , pp. 347 - 348
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Abramson, M., Explicit expressions for a class or permutation problems, Canadian Mathematical Bulletin 7, (1964), 345–350.Google Scholar
2. Abramson, M., Restricted choices, ibid 8 (1965).Google Scholar
3. Kaplansky, I., Solution of the "Problemé des Menages", Bulletin American Mathematical Society 49 (1943), 784-785.Google Scholar