Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T11:47:43.043Z Has data issue: false hasContentIssue false
  • English
  • Français

Numbers with Almost all Convergents in a Cantor Set

Part of: Elementary number theory Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  03 December 2018

Damien Roy  and
Johannes Schleischitz
Damien Roy
Affiliation:
Department of Mathematics and Statistics, University of Ottawa, 150 Louis-Pasteur, Ottawa, ON, K1N 6N5 Email: [email protected]@univie.ac.at
Johannes Schleischitz
Affiliation:
Department of Mathematics and Statistics, University of Ottawa, 150 Louis-Pasteur, Ottawa, ON, K1N 6N5 Email: [email protected]@univie.ac.at
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1984, K. Mahler asked how well elements in the Cantor middle third set can be approximated by rational numbers from that set and by rational numbers outside of that set. We consider more general missing digit sets 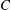$C$ and construct numbers in 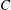$C$ that are arbitrarily well approximable by rationals in 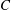$C$, but badly approximable by rationals outside of 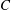$C$. More precisely, we construct them so that all but finitely many of their convergents lie in 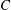$C$.

Keywords

Cantor setcontinued fractionDiophantine approximationparametric geometry of numbers

MSC classification

Primary: 11A55: Continued fractions
Secondary: 11J25: Diophantine inequalities 11J82: Measures of irrationality and of transcendence
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 4 , December 2019 , pp. 869 - 875
Copyright
© Canadian Mathematical Society 2018 

Footnotes

The research of J. Schleischitz was supported by the Schrödinger Scholarship J 3824 of the Austrian Science Fund (FWF), while that of D. Roy was partly supported by an NSERC discovery grant.

References

Bugeaud, Y., Diophantine approximation and Cantor sets . Math. Ann. 341(2008), 677–684. https://doi.org/10.1007/s00208-008-0209-4 Google Scholar
Fishman, L. and Simmons, D., Extrinsic Diophantine approximation on manifolds and fractals . J. Math. Pures Appl. 104(2015), 83–101. https://doi.org/10.1016/j.matpur.2015.02.002 Google Scholar
Mahler, K., Some suggestions for further research . Bull. Austral. Math. Soc. 29(1984), 101–108. https://doi.org/10.1017/S0004972700021316 Google Scholar
van der Poorten, A. J. and Shallit, J., Folded continued fractions . J. Number Theory 40(1992), 237–250. https://doi.org/10.1016/0022-314X(92)90042-N Google Scholar
Roy, D., On Schmidt and Summerer parametric geometry of numbers . Ann. of Math. 182(2015), 739–786. https://doi.org/10.4007/annals.2015.182.2.9 Google Scholar
Schleischitz, J., Generalizations of a result of Jarník on simultaneous approximation . Mosc. J. Combin. Number Theory 6(2016), 253–287.Google Scholar
Schmidt, W. M., Diophantine approximation . Lecture Notes in Mathematics, 785, Springer, Berlin, 1980.Google Scholar
Schmidt, W. M. and Summerer, L., Diophantine approximation and parametric geometry of numbers . Monatsh. Math. 169(2013), 51–104. https://doi.org/10.1007/s00605-012-0391-z Google Scholar
Shallit, J., Simple continued fractions for some irrational numbers . J. Number Theory 11(1979), 209–217. https://doi.org/10.1016/0022-314X(79)90040-4 Google Scholar