Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T04:02:04.154Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonexistence of Maxima for Perturbations of Some Inequalities with Critical Growth

Published online by Cambridge University Press:  20 November 2018

Alexander R. Pruss
Alexander R. Pruss*
Affiliation:
University of British Columbia, Vancouver, B.C. V6T 1Z2 e-mail:[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the question of nonexistence of extremal functions for perturbations of some sharp inequalities such as those of Moser-Trudinger (1971) and Chang- Marshall (1985). We shall show that for each critically sharp (in a sense that will be precisely defined) inequality of the form

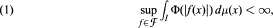
where 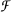is a collection of measurable functions on a finite measure space (I, μ) and O a nonnegative continuous function on [0, ∞), we have a continuous Ψ on [0, ∞) with 0 ≤ Ψ ≤ Φ, but with

not being attained even if the supremum in (1) is attained. We then apply our results to the Moser-Trudinger and Chang-Marshall inequalities. Our result is to be contrasted with the fact shown by Matheson and Pruss (1994) that if Ψ(t) = o(Φ(t) as t —> ∞ then the supremum in (2) is attained. In the present paper, we also give a converse to that fact.

Keywords

49J4528A2026A4630A10nonexistence of extremalslack of upper semicontinuitynonlinear functionalconvergence in measureMoser-Trudinger inequalityChang-Marshall inequalityDirichlet spaceDirichlet integraloptimization problems
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 39 , Issue 2 , 01 June 1996 , pp. 227 - 237
Copyright
Copyright © Canadian Mathematical Society 1996

References

1. Valentin Andreev, V. and Matheson, Alec, Extremal functions and the Chang-Marshall inequality, Pacific J. Math. 162(1994), 233–246.Google Scholar
2. Carleson, L. and Chang, S.-Y. A., On the existence of an extremal function for an inequality of J. Moser, Bull. Sc. Math. (2e série) 110(1986), 113–127.Google Scholar
3. Chang, S.-Y. A. and Marshall, D. E., On a sharp inequality concerning the Dirichlet integral, Amer. J. Math. 107(1985), 1015–1033.Google Scholar
4. Cima, Joseph and Matheson, Alec, A nonlinear functional on the Dirichlet space, J. Math. Anal. Appl. 191(1995), 380–401.Google Scholar
5. Essén, M., Sharp estimates of uniform harmonic majorants in the plane, Ark. Mat. 25(1987), 15–28.Google Scholar
6. Flores, Fabiân, The lack of lower semicontinuity and nonexistence ofminimizers, Nonlinear Anal. 23( 1994), 143–154.Google Scholar
7. Marshall, D. E., A new proof of a sharp inequality concerning the Dirichlet integral, Ark. Mat. 27(1989), 131–137.Google Scholar
8. Matheson, Alec and Pruss, Alexander R., Properties of extremal functions for some nonlinear functional on Dirichlet spaces, Trans. Amer. Math. Soc, to appear.Google Scholar
9. McLeod, J. B. and Peletier, L. A., Observations on Moser's inequality, Arch. Rational Mech. Anal. 106 (1989), 261–285.Google Scholar
10. Moser, J., A sharp form of an inequality by N. Trudinger, Indiana Univ. Math. J. 20(1971), 1077—1092.Google Scholar