Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T06:21:54.307Z Has data issue: false hasContentIssue false
  • English
  • Français

A New Class of Representations of EALA Coordinated by Quantum Tori in Two Variables

Published online by Cambridge University Press:  20 November 2018

S. Eswara Rao  and
Punita Batra
S. Eswara Rao
Affiliation:
School of Mathematics Tata Institute of Fundamental Research Homi Bhabha Road Mumbai 400 005 India, email: [email protected]
Punita Batra
Affiliation:
Department of Mathematics Harish-Chandra Research Institute Chhatnag Road Jhushi Allahabad 211 019 India, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the representations of extended affine Lie algebras 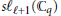$s{{\ell }_{\ell +1}}\left( {{\mathbb{C}}_{q}} \right)$ where $q$ is 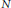$N$-th primitive root of unity (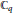$({{\mathbb{C}}_{q}}$ is the quantum torus in two variables). We first prove that 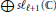$\oplus \,s{{\ell }_{\ell +1}}\left( \mathbb{C} \right)$ for a suitable number of copies is a quotient of 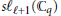$s{{\ell }_{\ell +1}}\left( {{\mathbb{C}}_{q}} \right)$. Thus any finite dimensional irreducible module for 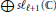$\oplus \,s{{\ell }_{\ell +1}}\left( \mathbb{C} \right)$lifts to a representation of 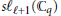$s{{\ell }_{\ell +1}}\left( {{\mathbb{C}}_{q}} \right)$. Conversely, we prove that any finite dimensional irreducible module for 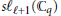$s{{\ell }_{\ell +1}}\left( {{\mathbb{C}}_{q}} \right)$ comes from above. We then construct modules for the extended affine Lie algebras 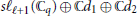$s{{\ell }_{\ell +1}}\left( {{\mathbb{C}}_{q}} \right)\oplus \mathbb{C}{{d}_{1}}\oplus \mathbb{C}{{d}_{2}}$ which is integrable and has finite dimensional weight spaces.

Keywords

17B6517B6617B68
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 45 , Issue 4 , 01 December 2002 , pp. 672 - 685
Copyright
Copyright © Canadian Mathematical Society 2002

References

[AABGP] Allison, B. N., Azam, S., Berman, S., Gao, Y. and Pianzola, A., Extended affine Lie algebras and their root systems. Mem. Amer. Math. Soc. (605) 126(1997).Google Scholar
[ABGP] Allison, B. N., Berman, S., Gao, Y. and Pianzola, A., GeA characterization of affine Kac Moody Lie algebras. Comm. Math. Phys. 185 (1997), 671–688.Google Scholar
[AG] Allison, B. N. and Gao, Y., The root system and the core of an extended affine Lie algebra. Submitted.Google Scholar
[BC] Berman, S. and Cox, B., Enveloping algebras and representations of toroidal Lie algebras. Pacific J. Math. 165 (1994), 239–267.Google Scholar
[BGK] Berman, S., Gao, Y. and Krylyuk, Y., Quantum tori and the structure of elliptic quasi-simple Lie algebras. J. Funct. Anal. 135 (1996), 339–389.Google Scholar
[BGKN] Berman, S., Gao, Y., Krylyuk, Y. and Neher, E., The alternative torus and the structure of elliptic quasi-simple Lie algebras of type A2 . Trans. Amer. Math. Soc. 347 (1995), 4315–4363.Google Scholar
[BS] Berman, S. and Szmigielski, J., Principal realization for extended affine Lie algebra of type sl2 with coordinates in a simple quantum torus with two variables. Preprint.Google Scholar
[E1] Eswara Rao, S., Iterated Loop Modules and a filteration for vertex Representations of Toroidal Lie algebras. Pacific J. Math. (2) 171 (1995), 511–528.Google Scholar
[E2] Eswara Rao, S., Classification of irreducible integrable modules for multi-loop algebras with finite dimensional weight spaces. J. Algebra 246 (2001), 215–225.Google Scholar
[E3] Eswara Rao, S., Classification of irreducible integrable modules for Toroidal Lie algebras with finite dimensional weight spaces. TIFR preprint, 2001.Google Scholar
[EF] Etingof, P. and Frenkel, I. B., Central extensions of current groups in two dimensions. Comm. Math. Phys. 165 (1994), 429–444.Google Scholar
[F] Frenkel, I. B., Representations of Kac-Moody algebras and dual resonance models. Lectures in Appl. Math. 21 (1985), 325–353.Google Scholar
[G1] Gao, Y., Vertex operators arising from the homogeneous realization for Comm. Math. Phys. 211 (2000), 745–777.Google Scholar
[G2] Gao, Y., Representations of Extended Affine Lie algebras coordinated by certain Quantum Tori. Compositio Math. 123 (2000), 1–25.Google Scholar
[H-KT] Hoegh-Krohn, R. and Torresani, B., Classification and construction of quasi-simple Lie algebras. J. Funct. Anal. 89 (1990), 106–136.Google Scholar
[K] Kac, V. G., Infinite dimensional Lie algebras. 3rd edition, Cambridge Univ. Press, 1990.Google Scholar
[M] Manin, Y. I., Topics in Noncommutative Geometry. Princeton Univ. Press, 1991.Google Scholar
[MEY] Moody, R. V., Eswara Rao, S. and Yokonuma, I., Toroidal Lie algebras and vertex representations. Geom. Dedicata 35 (1990), 283–307.Google Scholar
[RP] Pierce, Richard S., Associative Algebras. Graduate Texts in Math. 88, Springer Verlag, 1980.Google Scholar
[W] Wakimoto, M., Extended affine Lie algebras and a certain series of Hermitian representations. Preprint, 1985.Google Scholar
[Y] Yamada, H., Extended affine Lie algebras and their vertex representations. Publ. Res. Inst. Math. Sci. 25 (1989), 587–603.Google Scholar
[YO] Yoshii, Y., Jordan tori. C. R. Math. Rep. Acad. Sci. Canada 18 (1996), 153–158.Google Scholar
[Z] Zhao, K., The q-Virasoro-like algebra. J. Algebra (2) 188 (1997), 506–512.Google Scholar