Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T10:48:44.918Z Has data issue: false hasContentIssue false
  • English
  • Français

Lie Derivations in Prime Rings With Involution

Published online by Cambridge University Press:  20 November 2018

Gordon A. Swain  and
Philip S. Blau
Gordon A. Swain
Affiliation:
Mathematics Department Ashland University 401 College Avenue Ashland, Ohio 44805 USA, email: [email protected]
Philip S. Blau
Affiliation:
College of General Studies Boston University 871 Commonwealth Avenue Boston, Massachusetts 02215 USA, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

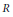Let $R$ be a non-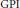$\text{GPI}$ prime ring with involution and characteristic 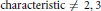$\ne 2,3$. Let 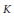$K$ denote the skew elements of 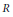$R$, and 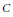$C$ denote the extended centroid of 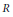$R$. Let 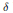$\delta$ be a Lie derivation of 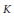$K$ into itself. Then 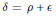$\delta \,=\,\rho \,+\,\varepsilon$ where $\varepsilon$ is an additive map into the skew elements of the extended centroid of 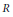$R$ which is zero on 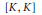$\left[ K,\,K \right]$, and 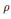$\rho$ can be extended to an ordinary derivation of 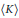$\left\langle K \right\rangle$ into 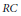$RC$, the central closure.

Keywords

16W1016N6016W25
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 3 , 01 September 1999 , pp. 401 - 411
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Beidar, K. I., Martindale, W. S. 3rd, and Mikhalev, A. V., Lie isomorphisms in prime rings with involution. J. Algebra 169 (1994), 304–327.Google Scholar
[2] Blau, P. S., Lie isomorphisms of non-GPI rings with involution, to appear.Google Scholar
[3] Herstein, I. N., Topics in Ring Theory. University of Chicago Press, Chicago, 1969.Google Scholar
[4] Martindale, W. S. 3rd, Prime rings with involution and generalized polynomial identities. J. Algebra 22 (1972), 502–516.Google Scholar
[5] Martindale, W. S. 3rd and Miers, C. R., Herstein's Lie theory revisited. J. Algebra 98 (1986), 14–37.Google Scholar
[6] Swain, G. A., Lie derivations of the skew elements of prime rings with involution. J. Algebra 184 (1996), 679–704.Google Scholar