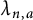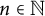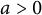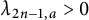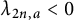1 Introduction and statement of main results
1.1 Li coefficients
The Riemann hypothesis (RH) is a critical question in analytic number theory. As such, it is interesting to examine different ways to frame it, which may shed more light on its resolution. In 1997, Xian-Jin Li has discovered a new positivity criterion for the RH. In [Reference Li10], he defined the Li coefficients for the Riemann zeta function as
where
![]() $\xi $
is the completed Riemann zeta function defined by
$\xi $
is the completed Riemann zeta function defined by
which satisfies
![]() $\xi (s)=\xi (1-s)$
and gave a simple equivalence criterion for the RH: RH is true if and only if these coefficients are nonnegative for every positive integer n. The Li coefficients
$\xi (s)=\xi (1-s)$
and gave a simple equivalence criterion for the RH: RH is true if and only if these coefficients are nonnegative for every positive integer n. The Li coefficients
![]() $\lambda _{n}$
can be written as follows:
$\lambda _{n}$
can be written as follows:
 $$ \begin{align*} \lambda_{n}=\sum_{\rho}^{\ast}\left[1- \left(1-\frac{1}{\rho}\right)^{n}\right]=\lim_{T\to\infty}\sum_{\rho; \lvert {\mathrm{Im}}(\rho) \rvert \leq T}\left[1-\left(1-\frac{1}{\rho}\right)^{n}\right], \end{align*} $$
$$ \begin{align*} \lambda_{n}=\sum_{\rho}^{\ast}\left[1- \left(1-\frac{1}{\rho}\right)^{n}\right]=\lim_{T\to\infty}\sum_{\rho; \lvert {\mathrm{Im}}(\rho) \rvert \leq T}\left[1-\left(1-\frac{1}{\rho}\right)^{n}\right], \end{align*} $$
where the sum runs over the nontrivial zeros of the Riemann zeta function counted with multiplicity. This criterion is generalized by Bombieri and Lagarias [Reference Bombieri and Lagarias4] for any arbitrarily multiset of numbers assuming certain convergence conditions. Voros [Reference Voros19, Section 3.3] has proved that the RH true is equivalent to the growth of
![]() $\lambda _{n}$
as
$\lambda _{n}$
as
![]() $\frac {1}{2}n \log n$
determined by its archimedean part, while the RH false is equivalent to the oscillations of
$\frac {1}{2}n \log n$
determined by its archimedean part, while the RH false is equivalent to the oscillations of
![]() $\lambda _{n}$
with exponentially growing amplitude, determined by its finite part. The Li coefficients were generalized in two ways: by generalizing these coefficients to various sets of functions (the Selberg class, the class of automorphic L-functions, zeta function on function fields,…[Reference Lagarias8, Reference Mazhouda and Smajlović11, Reference Smajlović17]) and by introducing new parameter in its definition (see [Reference Mazhouda and Sodaïgui12]). The Li coefficients (and its generalizations) have generated a lot of research interest due to its applicability and simplicity.
$\lambda _{n}$
with exponentially growing amplitude, determined by its finite part. The Li coefficients were generalized in two ways: by generalizing these coefficients to various sets of functions (the Selberg class, the class of automorphic L-functions, zeta function on function fields,…[Reference Lagarias8, Reference Mazhouda and Smajlović11, Reference Smajlović17]) and by introducing new parameter in its definition (see [Reference Mazhouda and Sodaïgui12]). The Li coefficients (and its generalizations) have generated a lot of research interest due to its applicability and simplicity.
1.2 Quadrilateral zeta function
Recall the definitions of Hurwitz and periodic zeta functions. The Hurwitz zeta function
![]() $\zeta (s,a)$
is defined by the series
$\zeta (s,a)$
is defined by the series
 $$\begin{align*}\zeta (s,a) := \sum_{n=0}^\infty \frac{1}{(n+a)^s}, \qquad \sigma>1, \quad 0<a \le 1. \end{align*}$$
$$\begin{align*}\zeta (s,a) := \sum_{n=0}^\infty \frac{1}{(n+a)^s}, \qquad \sigma>1, \quad 0<a \le 1. \end{align*}$$
The function
![]() $\zeta (s,a)$
is a meromorphic function with a simple pole at
$\zeta (s,a)$
is a meromorphic function with a simple pole at
![]() $s=1$
whose residue is
$s=1$
whose residue is
![]() $1$
(see, for example, [Reference Apostol1, Section 12]). The periodic zeta function
$1$
(see, for example, [Reference Apostol1, Section 12]). The periodic zeta function
![]() ${\mathrm {Li}}_s (e^{2\pi ia})$
is defined by
${\mathrm {Li}}_s (e^{2\pi ia})$
is defined by
 $$\begin{align*}{\mathrm{Li}}_s (e^{2\pi ia}) := \sum_{n=1}^\infty \frac{e^{2\pi ina}}{n^s}, \qquad \sigma>1, \quad 0<a \le 1 \end{align*}$$
$$\begin{align*}{\mathrm{Li}}_s (e^{2\pi ia}) := \sum_{n=1}^\infty \frac{e^{2\pi ina}}{n^s}, \qquad \sigma>1, \quad 0<a \le 1 \end{align*}$$
(see, for instance, [Reference Apostol1, Exercise 12.2]). Note that the function
![]() ${\mathrm {Li}}_s (e^{2\pi ia})$
with
${\mathrm {Li}}_s (e^{2\pi ia})$
with
![]() $0<a<1$
is analytically continuable to the whole complex plane since
$0<a<1$
is analytically continuable to the whole complex plane since
![]() ${\mathrm {Li}}_s (e^{2\pi ia})$
does not have any pole, that is shown by the fact that the Dirichlet series of
${\mathrm {Li}}_s (e^{2\pi ia})$
does not have any pole, that is shown by the fact that the Dirichlet series of
![]() ${\mathrm {Li}}_s (e^{2\pi ia})$
converges uniformly in each compact subset of the half-plane
${\mathrm {Li}}_s (e^{2\pi ia})$
converges uniformly in each compact subset of the half-plane
![]() $\sigma>0$
when
$\sigma>0$
when
![]() $0<a<1$
(see, for example, [Reference Laurinčikas and Garunkštis9, p. 20]). For
$0<a<1$
(see, for example, [Reference Laurinčikas and Garunkštis9, p. 20]). For
![]() $0 <a \le 1/2$
, we define zeta functions
$0 <a \le 1/2$
, we define zeta functions
 $$ \begin{align*} \begin{aligned} &Z(s,a) := \zeta (s,a) + \zeta (s,1-a), \qquad P(s,a) := {\mathrm{Li}}_s (e^{2\pi ia}) + {\mathrm{Li}}_s (e^{2\pi i(1-a)}), \\ &2Q(s,a) := Z(s,a) + P(s,a) , \qquad \xi_Q (s,a) := s(s-1) \pi^{-s/2} \Gamma (s/2) Q(s,a). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &Z(s,a) := \zeta (s,a) + \zeta (s,1-a), \qquad P(s,a) := {\mathrm{Li}}_s (e^{2\pi ia}) + {\mathrm{Li}}_s (e^{2\pi i(1-a)}), \\ &2Q(s,a) := Z(s,a) + P(s,a) , \qquad \xi_Q (s,a) := s(s-1) \pi^{-s/2} \Gamma (s/2) Q(s,a). \end{aligned} \end{align*} $$
We can see that
![]() $Q(s,a)$
is meromorphic functions with a simple pole at
$Q(s,a)$
is meromorphic functions with a simple pole at
![]() $s=1$
. In addition, we have
$s=1$
. In addition, we have
![]() $Q(0,a)=-1/2=\zeta (0)$
and
$Q(0,a)=-1/2=\zeta (0)$
and
![]() $\xi _Q(s,a) = \xi _Q(1-s,a)$
, which is proved by
$\xi _Q(s,a) = \xi _Q(1-s,a)$
, which is proved by
(see [Reference Nakamura13, Theorem 1.1]). Moreover, the function
![]() $Q(s,a)$
has the following properties. When
$Q(s,a)$
has the following properties. When
![]() $a=1/6, 1/4, 1/3$
, and
$a=1/6, 1/4, 1/3$
, and
![]() $1/2$
, the RH holds true if and only if all nonreal zeros of
$1/2$
, the RH holds true if and only if all nonreal zeros of
![]() $Q(s,a)$
are on the line
$Q(s,a)$
are on the line
![]() ${\mathrm {Re}}(s)=1/2$
(see [Reference Nakamura14, Proposition 1.3]). Let
${\mathrm {Re}}(s)=1/2$
(see [Reference Nakamura14, Proposition 1.3]). Let
![]() $N_{\mathrm {Q}}^{\mathrm {CL}} (T)$
be the number of the zeros of
$N_{\mathrm {Q}}^{\mathrm {CL}} (T)$
be the number of the zeros of
![]() $Q(s,a)$
on the line segment from
$Q(s,a)$
on the line segment from
![]() $1/2$
to
$1/2$
to
![]() $1/2 +iT$
. In [Reference Nakamura13, Theorem 1.2], the third author proved that for any
$1/2 +iT$
. In [Reference Nakamura13, Theorem 1.2], the third author proved that for any
![]() $0 < a \le 1/2$
, there exist positive constants
$0 < a \le 1/2$
, there exist positive constants
![]() $A(a)$
and
$A(a)$
and
![]() $T_0(a)$
such that
$T_0(a)$
such that
Next, let
![]() $N_{F}(T)$
count the number of nonreal zeros of a function
$N_{F}(T)$
count the number of nonreal zeros of a function
![]() $F(s)$
having
$F(s)$
having
![]() $|{\mathrm {Im}}(s)|<T$
. Then, for any
$|{\mathrm {Im}}(s)|<T$
. Then, for any
![]() $0<a\leq 1/2$
,
$0<a\leq 1/2$
,
and the third author [Reference Nakamura14, Proposition 1.8] proved that
Furthermore, he [Reference Nakamura14, Theorem 1.1] proved that there is a unique absolute
![]() $a_{0}\in {(0,1/2)}$
such that
$a_{0}\in {(0,1/2)}$
such that
In addition, it is proved in [Reference Nakamura14, Corollary 1.2] that all real zeros of
![]() $Q(s,a)$
are simple and are located only at the negative even integers just like
$Q(s,a)$
are simple and are located only at the negative even integers just like
![]() $\zeta (s)$
if and only if
$\zeta (s)$
if and only if
![]() ${a_0 < a \le 1/2}$
. Let us note by
${a_0 < a \le 1/2}$
. Let us note by
![]() $Z_Q$
the set of all nontrivial zeros
$Z_Q$
the set of all nontrivial zeros
![]() $\rho _{a}$
of
$\rho _{a}$
of
![]() $\xi _{Q}(s,a)$
. Since it is an entire function of order 1, one has
$\xi _{Q}(s,a)$
. Since it is an entire function of order 1, one has
 $$ \begin{align} \xi_{Q}(s,a)=e^{A+Bs}\prod_{\rho_{a}\in{Z_{Q}}}\left(1-\frac{s}{\rho_{a}}\right)e^{\frac{s}{\rho_{a}}} =\xi_{Q}(0,a)\prod_{\rho_{a}\in{Z_{Q}}}\left(1-\frac{s}{\rho_{a}}\right), \end{align} $$
$$ \begin{align} \xi_{Q}(s,a)=e^{A+Bs}\prod_{\rho_{a}\in{Z_{Q}}}\left(1-\frac{s}{\rho_{a}}\right)e^{\frac{s}{\rho_{a}}} =\xi_{Q}(0,a)\prod_{\rho_{a}\in{Z_{Q}}}\left(1-\frac{s}{\rho_{a}}\right), \end{align} $$
where
![]() $e^{A}=1/2,\ B=\frac {Q'}{Q}(0,a)-1-\frac {\gamma +\log \pi }{2}$
, and
$e^{A}=1/2,\ B=\frac {Q'}{Q}(0,a)-1-\frac {\gamma +\log \pi }{2}$
, and
![]() $\gamma $
denotes the Euler constant. Note that
$\gamma $
denotes the Euler constant. Note that
![]() $Q'(0,a)$
is given explicitly in [Reference Nakamura14, Theorem 1.5].
$Q'(0,a)$
is given explicitly in [Reference Nakamura14, Theorem 1.5].
1.3 Main results
Recall that
![]() $\zeta (1-s) = \Gamma _{\!\! {\mathrm {cos}}} (s) \zeta (s)$
and
$\zeta (1-s) = \Gamma _{\!\! {\mathrm {cos}}} (s) \zeta (s)$
and
![]() $Q(1-s,a) = \Gamma _{\!\! {\mathrm {cos}}} (s) Q(s,a)$
by (1.1). However, the function
$Q(1-s,a) = \Gamma _{\!\! {\mathrm {cos}}} (s) Q(s,a)$
by (1.1). However, the function
![]() $Q(s,a)$
does not have an Euler product except for
$Q(s,a)$
does not have an Euler product except for
![]() $a=1/6, 1/4, 1/3$
, and
$a=1/6, 1/4, 1/3$
, and
![]() $1/2$
. Hence, the function
$1/2$
. Hence, the function
![]() $Q(s, a)$
is a suitable object to consider the influence of not Riemann’s functional equation but an Euler product to zeros of zeta functions. We show a criterion for nonvanishing of
$Q(s, a)$
is a suitable object to consider the influence of not Riemann’s functional equation but an Euler product to zeros of zeta functions. We show a criterion for nonvanishing of
![]() $Q(s,a)$
in terms of the positivity of the Li coefficients, an arithmetic and asymptotic formula for these coefficients in Theorems 1.1, 1.2, and 1.4, respectively. It should be emphasized that
$Q(s,a)$
in terms of the positivity of the Li coefficients, an arithmetic and asymptotic formula for these coefficients in Theorems 1.1, 1.2, and 1.4, respectively. It should be emphasized that
![]() $\lambda _{n,a}$
defined in (1.3) are the first Li coefficients that we can explicitly give
$\lambda _{n,a}$
defined in (1.3) are the first Li coefficients that we can explicitly give
![]() $n \in {\mathbb {N}}$
such that
$n \in {\mathbb {N}}$
such that
![]() $\lambda _{n,a} <0$
. There is a possibility that this fact would give an idea to find negative Li coefficients for
$\lambda _{n,a} <0$
. There is a possibility that this fact would give an idea to find negative Li coefficients for
![]() $\zeta (s)$
if they would exist.
$\zeta (s)$
if they would exist.
For
![]() $n\neq 0$
, the Li coefficients attached to
$n\neq 0$
, the Li coefficients attached to
![]() $Q(s,a)$
nonvanishing at zero are defined by the sum
$Q(s,a)$
nonvanishing at zero are defined by the sum
 $$ \begin{align*} \lambda_{n,a}:=\sum_{\rho_{a}\in{Z_{Q}}}^{*}\left(1-\left(1-\frac{1}{\rho_{a}}\right)^{n}\right)= \lim_{T\longmapsto \infty}\sum_{|{\mathrm{Im}}(\rho_{a})|\leq T}^{*}\left(1-\left(1-\frac{1}{\rho_{a}}\right)^{n}\right). \end{align*} $$
$$ \begin{align*} \lambda_{n,a}:=\sum_{\rho_{a}\in{Z_{Q}}}^{*}\left(1-\left(1-\frac{1}{\rho_{a}}\right)^{n}\right)= \lim_{T\longmapsto \infty}\sum_{|{\mathrm{Im}}(\rho_{a})|\leq T}^{*}\left(1-\left(1-\frac{1}{\rho_{a}}\right)^{n}\right). \end{align*} $$
The symmetry
![]() $\rho _{a}\longmapsto 1-\rho _{a}$
in the set
$\rho _{a}\longmapsto 1-\rho _{a}$
in the set
![]() $Z_Q$
of nontrivial zeros of
$Z_Q$
of nontrivial zeros of
![]() $Q(s,a)$
implies that
$Q(s,a)$
implies that
![]() $\lambda _{-n,a}=\overline {\lambda _{n,a}}=\lambda _{n,a}$
for all
$\lambda _{-n,a}=\overline {\lambda _{n,a}}=\lambda _{n,a}$
for all
![]() $n\in {\mathbb {N}}$
. So,
$n\in {\mathbb {N}}$
. So,
![]() $\lambda _{n,a}$
are real. We have also
$\lambda _{n,a}$
are real. We have also
Moreover, from (1.2), we have (see [Reference Bombieri and Lagarias4, Equations (2.3) and (2.4)] or [Reference Smajlović17, Appendix A])
 $$ \begin{align*} \sum_{n=0}^{\infty}\lambda_{n+1,a}s^{n}=\frac{d}{ds}\log \left[\xi_{Q}\left(\frac{1}{1-s},a\right)\right].\end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty}\lambda_{n+1,a}s^{n}=\frac{d}{ds}\log \left[\xi_{Q}\left(\frac{1}{1-s},a\right)\right].\end{align*} $$
As an analogue of Li coefficients for the Riemann zeta function, we have the following.
Theorem 1.1 The function
![]() $Q(s,a)$
does not vanish when
$Q(s,a)$
does not vanish when
![]() $\mathrm {Re} (s)>1/2$
if and only if
$\mathrm {Re} (s)>1/2$
if and only if
![]() $\lambda _{n,a} \geq 0$
for all
$\lambda _{n,a} \geq 0$
for all
![]() $n \in {\mathbb {N}}$
.
$n \in {\mathbb {N}}$
.
An arithmetic formula for
![]() $\lambda _{n,a}$
is stated in the following theorems.
$\lambda _{n,a}$
is stated in the following theorems.
Theorem 1.2 We have
 $$\begin{align*}\lambda_{n,a} = 1-\frac{n}{2}(\log(4\pi)+\gamma)+\sum_{k=2}^{n}(-1)^{k}\binom{n}{k} \left(1-2^{-k}\right)\zeta(k)+\sum_{k=1}^{n}\binom{n}{k}\gamma_{Q}(k-1), \end{align*}$$
$$\begin{align*}\lambda_{n,a} = 1-\frac{n}{2}(\log(4\pi)+\gamma)+\sum_{k=2}^{n}(-1)^{k}\binom{n}{k} \left(1-2^{-k}\right)\zeta(k)+\sum_{k=1}^{n}\binom{n}{k}\gamma_{Q}(k-1), \end{align*}$$
where
![]() $\gamma _{Q}(n)$
are defined as follows:
$\gamma _{Q}(n)$
are defined as follows:
 $$ \begin{align*} \frac{Q'}{Q}(s+1,a)+\frac{1}{s}=\sum_{n=0}^{\infty}\gamma_{Q}(n)s^{n}. \end{align*} $$
$$ \begin{align*} \frac{Q'}{Q}(s+1,a)+\frac{1}{s}=\sum_{n=0}^{\infty}\gamma_{Q}(n)s^{n}. \end{align*} $$
Theorem 1.3 For
![]() $a=1/2,1/3,1/4,1/6$
, under the RH, we have
$a=1/2,1/3,1/4,1/6$
, under the RH, we have
For a fixed
![]() $l \in {\mathbb {N}}$
, we have the following asymptotic formula of
$l \in {\mathbb {N}}$
, we have the following asymptotic formula of
![]() $\lambda _{l,a}$
when
$\lambda _{l,a}$
when
![]() $a \to +0$
. We can see that there exists
$a \to +0$
. We can see that there exists
![]() $n \in {\mathbb {N}}$
such that
$n \in {\mathbb {N}}$
such that
![]() $\lambda _{n,a} <0$
by Theorem 1.1 and the fact that
$\lambda _{n,a} <0$
by Theorem 1.1 and the fact that
![]() $Q(s,a)$
does not satisfy an analogue of the RH when
$Q(s,a)$
does not satisfy an analogue of the RH when
![]() $a \in {\mathbb {Q}} \cap (0,1/2) \backslash \{1/6, 1/4, 1/3\}$
(see [Reference Nakamura14, Proposition 1.4]). Clearly, this argument gives no information on the frequency of
$a \in {\mathbb {Q}} \cap (0,1/2) \backslash \{1/6, 1/4, 1/3\}$
(see [Reference Nakamura14, Proposition 1.4]). Clearly, this argument gives no information on the frequency of
![]() $n \in {\mathbb {N}}$
, the smallest
$n \in {\mathbb {N}}$
, the smallest
![]() $n \in {\mathbb {N}}$
such that
$n \in {\mathbb {N}}$
such that
![]() $\lambda _{n,a} <0$
and so on. However, the next theorem implies that
$\lambda _{n,a} <0$
and so on. However, the next theorem implies that
![]() $\lambda _{2n,a} <0$
if we fix any
$\lambda _{2n,a} <0$
if we fix any
![]() $n \in {\mathbb {N}}$
and then we take
$n \in {\mathbb {N}}$
and then we take
![]() $a>0$
sufficiently small.
$a>0$
sufficiently small.
Theorem 1.4 Fix
![]() $l \in {\mathbb {N}}$
. Then it holds that
$l \in {\mathbb {N}}$
. Then it holds that
 $$\begin{align*}\lambda_{l,a} = \frac{(-1)^{l+1}}{(2a)^l} + O_l \bigl( a^{1-l} |\log a| \bigr), \qquad a \to +0. \end{align*}$$
$$\begin{align*}\lambda_{l,a} = \frac{(-1)^{l+1}}{(2a)^l} + O_l \bigl( a^{1-l} |\log a| \bigr), \qquad a \to +0. \end{align*}$$
Especially, for any fixed
![]() $n \in {\mathbb {N}}$
, there are
$n \in {\mathbb {N}}$
, there are
![]() $a>0$
such that
$a>0$
such that
2 Proofs
2.1 Proof of Theorem 1.1
Since
![]() $\lambda _{-n,a}=\overline {\lambda _{n,a}}=\lambda _{n,a}$
for all
$\lambda _{-n,a}=\overline {\lambda _{n,a}}=\lambda _{n,a}$
for all
![]() $n\in {\mathbb {N}}$
, then
$n\in {\mathbb {N}}$
, then
![]() $\mathrm {Re}(\lambda _{-n,a})=\mathrm {Re}(\lambda _{n,a}) =\lambda _{n,a}$
. Using that
$\mathrm {Re}(\lambda _{-n,a})=\mathrm {Re}(\lambda _{n,a}) =\lambda _{n,a}$
. Using that
![]() $\xi _{Q}(s,a)$
is an entire function of order 1, and its zeros lie in the critical strip
$\xi _{Q}(s,a)$
is an entire function of order 1, and its zeros lie in the critical strip
![]() ${0< \mathrm {Re}(s)<1}$
, we obtain that the series
${0< \mathrm {Re}(s)<1}$
, we obtain that the series
![]() $\sum _{\rho \in {Z_{Q}}}\frac {1+|\mathrm {Re}(\rho )|}{(1+|\rho |)^{2}}$
is convergent. Application of [Reference Bombieri and Lagarias4, Theorem 1] to the multiset
$\sum _{\rho \in {Z_{Q}}}\frac {1+|\mathrm {Re}(\rho )|}{(1+|\rho |)^{2}}$
is convergent. Application of [Reference Bombieri and Lagarias4, Theorem 1] to the multiset
![]() $Z_{Q}$
of zeros of
$Z_{Q}$
of zeros of
![]() $Q(s,a)$
gives that
$Q(s,a)$
gives that
![]() $\mathrm {Re}(\rho )\leq 1/2$
if and only if
$\mathrm {Re}(\rho )\leq 1/2$
if and only if
![]() $\lambda _{n,a}\geq 0$
for all
$\lambda _{n,a}\geq 0$
for all
![]() $n\in {\mathbb {N}}$
. Now, the application of the same theorem to the multiset
$n\in {\mathbb {N}}$
. Now, the application of the same theorem to the multiset
![]() $1-Z_{Q}=Z_{Q}$
gives
$1-Z_{Q}=Z_{Q}$
gives
![]() $\mathrm {Re}(\rho )\geq 1/2$
if and only if
$\mathrm {Re}(\rho )\geq 1/2$
if and only if
![]() $\lambda _{n,a}\geq 0$
. This completes the proof.
$\lambda _{n,a}\geq 0$
. This completes the proof.
Theorem 1.1 can also be proved by the same argument used in [Reference Brown5, Theorem 1], which is due to Oesterlé.
2.2 Proof of Theorem 1.2
From the expression of
![]() $\xi _{Q}(s,a)$
, one has
$\xi _{Q}(s,a)$
, one has
 $$ \begin{align*}\frac{\xi'_{Q}}{\xi_{Q}}(s,a)=\frac{1}{s}+\frac{1}{s-1}- \frac{1}{2}\log\pi+\frac{1}{2}\frac{\Gamma'}{\Gamma}(s/2)+\frac{Q'}{Q}(s,a),\end{align*} $$
$$ \begin{align*}\frac{\xi'_{Q}}{\xi_{Q}}(s,a)=\frac{1}{s}+\frac{1}{s-1}- \frac{1}{2}\log\pi+\frac{1}{2}\frac{\Gamma'}{\Gamma}(s/2)+\frac{Q'}{Q}(s,a),\end{align*} $$
which is rewritten as
 $$ \begin{align} \frac{\xi'_{Q}}{\xi_{Q}}(s+1,a)=\frac{1}{s+1}+\frac{1}{s}-\frac{1}{2}\log\pi+ \frac{1}{2}\frac{\Gamma'}{\Gamma}((s+1)/2)+\frac{Q'}{Q}(s+1,a). \end{align} $$
$$ \begin{align} \frac{\xi'_{Q}}{\xi_{Q}}(s+1,a)=\frac{1}{s+1}+\frac{1}{s}-\frac{1}{2}\log\pi+ \frac{1}{2}\frac{\Gamma'}{\Gamma}((s+1)/2)+\frac{Q'}{Q}(s+1,a). \end{align} $$
Note that
![]() $Q(s,a)$
is a meromorphic function on the whole complex plane, which is holomorphic everywhere except for a simple pole at
$Q(s,a)$
is a meromorphic function on the whole complex plane, which is holomorphic everywhere except for a simple pole at
![]() $s = 1$
with residue 1 (see [Reference Nakamura13, Section 2.1]). Let us define the coefficients
$s = 1$
with residue 1 (see [Reference Nakamura13, Section 2.1]). Let us define the coefficients
![]() $\gamma _{Q}(n)$
and
$\gamma _{Q}(n)$
and
![]() $\tau _{Q}(n)$
as follows:
$\tau _{Q}(n)$
as follows:
 $$ \begin{align} \frac{Q'}{Q}(s+1,a)+\frac{1}{s}=\sum_{n=0}^{\infty}\gamma_{Q}(n)s^{n} \end{align} $$
$$ \begin{align} \frac{Q'}{Q}(s+1,a)+\frac{1}{s}=\sum_{n=0}^{\infty}\gamma_{Q}(n)s^{n} \end{align} $$
and
 $$ \begin{align} -\frac{1}{2}\log\pi+\frac{1}{2}\frac{\Gamma'}{\Gamma}((s+1)/2)=\sum_{n=0}^{\infty}\tau_{Q}(n)s^{n}. \end{align} $$
$$ \begin{align} -\frac{1}{2}\log\pi+\frac{1}{2}\frac{\Gamma'}{\Gamma}((s+1)/2)=\sum_{n=0}^{\infty}\tau_{Q}(n)s^{n}. \end{align} $$
By Equation (1.2), one has
 $$ \begin{align*} \log\xi_{Q}(s,a)=\log\xi_{Q}(0,a)-\sum_{\rho_{a}\in{Z_{Q}}}\sum_{m=1}^{\infty}\frac{1}{m\rho^{m}}s^{m}. \end{align*} $$
$$ \begin{align*} \log\xi_{Q}(s,a)=\log\xi_{Q}(0,a)-\sum_{\rho_{a}\in{Z_{Q}}}\sum_{m=1}^{\infty}\frac{1}{m\rho^{m}}s^{m}. \end{align*} $$
From the functional equation for the function
![]() $\xi _{Q}(s,a)$
, in the neighborhood of
$\xi _{Q}(s,a)$
, in the neighborhood of
![]() $s=0$
, we have
$s=0$
, we have
 $$ \begin{align} \frac{\xi_{Q}^{\prime}}{\xi_{Q}}(s+1,a)=-\frac{\xi_{Q}^{\prime}}{\xi_{Q}} (-s,a)=\sum_{m=0}^{\infty}(-1)^{m}\sum_{\rho_{a}\in{Z_{Q}}}\frac{1}{\rho^{m+1}}s^{m}. \end{align} $$
$$ \begin{align} \frac{\xi_{Q}^{\prime}}{\xi_{Q}}(s+1,a)=-\frac{\xi_{Q}^{\prime}}{\xi_{Q}} (-s,a)=\sum_{m=0}^{\infty}(-1)^{m}\sum_{\rho_{a}\in{Z_{Q}}}\frac{1}{\rho^{m+1}}s^{m}. \end{align} $$
Comparing Equations (2.1)–(2.4), we get
 $$ \begin{align*} (-1)^{m}\sum_{\rho_{a}\in{Z_{Q}}}\frac{1}{\rho^{m+1}} =(-1)^{m}+\gamma_{Q}(m)+\tau_{Q}(m), \end{align*} $$
$$ \begin{align*} (-1)^{m}\sum_{\rho_{a}\in{Z_{Q}}}\frac{1}{\rho^{m+1}} =(-1)^{m}+\gamma_{Q}(m)+\tau_{Q}(m), \end{align*} $$
for
![]() $m\geq 0$
. Hence, the definition of
$m\geq 0$
. Hence, the definition of
![]() $\lambda _{n,a}$
yields
$\lambda _{n,a}$
yields
 $$ \begin{align*} \lambda_{n,a}=\sum_{k=1}^{n}(-1)^{k-1}\binom{n}{k}\sum_{\rho_{a}\in{Z_{Q}}}\frac{1}{\rho^{k}}=1+ \sum_{k=1}^{n}\binom{n}{k}\gamma_{Q}(k-1)+\sum_{k=1}^{n}\binom{n}{k}\tau_{Q}(k-1), \end{align*} $$
$$ \begin{align*} \lambda_{n,a}=\sum_{k=1}^{n}(-1)^{k-1}\binom{n}{k}\sum_{\rho_{a}\in{Z_{Q}}}\frac{1}{\rho^{k}}=1+ \sum_{k=1}^{n}\binom{n}{k}\gamma_{Q}(k-1)+\sum_{k=1}^{n}\binom{n}{k}\tau_{Q}(k-1), \end{align*} $$
where
 $$ \begin{align*} \tau_{Q}(0)=-\frac{1}{2}\log\pi+\frac{1}{2}\psi(1/2)\ \mbox{and}\ \tau_{Q}(k-1)=(-1)^{k} \sum_{m=0}^{\infty}\frac{1}{(2m+1)^{k}} \end{align*} $$
$$ \begin{align*} \tau_{Q}(0)=-\frac{1}{2}\log\pi+\frac{1}{2}\psi(1/2)\ \mbox{and}\ \tau_{Q}(k-1)=(-1)^{k} \sum_{m=0}^{\infty}\frac{1}{(2m+1)^{k}} \end{align*} $$
using that
![]() $\psi (z)=-\gamma -\frac {1}{z}+\sum _{k=1}^{\infty }\frac {z}{k(k+z)}$
. Here,
$\psi (z)=-\gamma -\frac {1}{z}+\sum _{k=1}^{\infty }\frac {z}{k(k+z)}$
. Here,
![]() $\psi (s)=\frac {\Gamma '}{\Gamma }(s)$
is the logarithmic derivative of the Gamma function. Since
$\psi (s)=\frac {\Gamma '}{\Gamma }(s)$
is the logarithmic derivative of the Gamma function. Since
![]() $\psi (1/2)=-\gamma -2\log 2$
, we obtain
$\psi (1/2)=-\gamma -2\log 2$
, we obtain
 $$ \begin{align*} \lambda_{n,a}&=1-\frac{n}{2}(\log(4\pi)+\gamma)+\sum_{k=2}^{n}(-1)^{k} \binom{n}{k}\sum_{m=0}^{\infty}\frac{1}{(2m+1)^{k}} +\sum_{k=1}^{n}\binom{n}{k}\gamma_{Q}(k-1)\\ &=1-\frac{n}{2}(\log(4\pi)+\gamma)+\sum_{k=2}^{n}(-1)^{k}\binom{n}{k} \left(1-2^{-k}\right)\zeta(k)+\sum_{k=1}^{n}\binom{n}{k}\gamma_{Q}(k-1). \end{align*} $$
$$ \begin{align*} \lambda_{n,a}&=1-\frac{n}{2}(\log(4\pi)+\gamma)+\sum_{k=2}^{n}(-1)^{k} \binom{n}{k}\sum_{m=0}^{\infty}\frac{1}{(2m+1)^{k}} +\sum_{k=1}^{n}\binom{n}{k}\gamma_{Q}(k-1)\\ &=1-\frac{n}{2}(\log(4\pi)+\gamma)+\sum_{k=2}^{n}(-1)^{k}\binom{n}{k} \left(1-2^{-k}\right)\zeta(k)+\sum_{k=1}^{n}\binom{n}{k}\gamma_{Q}(k-1). \end{align*} $$
The equality above implies Theorem 1.2.
2.3 Proof of Theorem 1.3
Let us note that
 $$ \begin{align*} \sum_{k=2}^{n}(-1)^{k}\binom{n}{k}\left(1-2^{-k}\right)\zeta(k)= \sum_{k=2}^{n}(-1)^{l}\binom{n}{k}\frac{\zeta(k,1/2)}{2^{k}}, \end{align*} $$
$$ \begin{align*} \sum_{k=2}^{n}(-1)^{k}\binom{n}{k}\left(1-2^{-k}\right)\zeta(k)= \sum_{k=2}^{n}(-1)^{l}\binom{n}{k}\frac{\zeta(k,1/2)}{2^{k}}, \end{align*} $$
where
![]() $\zeta (s, a)$
is the Hurwitz zeta function defined in Section 1.2. With the notation of Flajolet and Vespas [Reference Flajolet and Vepstas7, Lines 2–4, p. 70], this is
$\zeta (s, a)$
is the Hurwitz zeta function defined in Section 1.2. With the notation of Flajolet and Vespas [Reference Flajolet and Vepstas7, Lines 2–4, p. 70], this is
![]() $A_{n}(1,2)$
and which is equal to
$A_{n}(1,2)$
and which is equal to
where the o(1) error term above is exponentially small and oscillating and equal to
 $$ \begin{align*} \frac{1}{2}\left(\frac{n}{\pi}\right)^{1/4}\exp(-\sqrt{2\pi n})\cos\left(\sqrt{2\pi n}-\frac{5\pi}{8}\right)+O\left(n^{-1/4}e^{-\sqrt{2\pi n}}\right). \end{align*} $$
$$ \begin{align*} \frac{1}{2}\left(\frac{n}{\pi}\right)^{1/4}\exp(-\sqrt{2\pi n})\cos\left(\sqrt{2\pi n}-\frac{5\pi}{8}\right)+O\left(n^{-1/4}e^{-\sqrt{2\pi n}}\right). \end{align*} $$
Then we have
 $$ \begin{align*} \lambda_{n,a}=\frac{n}{2}\log n+\frac{n}{2}\left(\gamma-1-\log 2\pi\right)+\sum_{k=1}^{n}\binom{n}{k}\gamma_{Q}(k-1)+O(1). \end{align*} $$
$$ \begin{align*} \lambda_{n,a}=\frac{n}{2}\log n+\frac{n}{2}\left(\gamma-1-\log 2\pi\right)+\sum_{k=1}^{n}\binom{n}{k}\gamma_{Q}(k-1)+O(1). \end{align*} $$
It remains to prove that
 $$ \begin{align} \sum_{k=1}^{n}\binom{n}{k}\gamma_{Q}(k-1)=O(\sqrt{n}\log n). \end{align} $$
$$ \begin{align} \sum_{k=1}^{n}\binom{n}{k}\gamma_{Q}(k-1)=O(\sqrt{n}\log n). \end{align} $$
To do so, we follow very closely the lines of the proof of the corresponding result in [Reference Lagarias8, Theorem 6.1] or [Reference Omar and Mazhouda16, Lemma 3.3] and it will be shortened. We use the following kernel function:
 $$ \begin{align*} k_{n}(s):=\left(1+\frac{1}{s}\right)^{n}-1=\sum_{k=1}^{n}\binom{n}{k} \frac{1}{s^{k}}. \end{align*} $$
$$ \begin{align*} k_{n}(s):=\left(1+\frac{1}{s}\right)^{n}-1=\sum_{k=1}^{n}\binom{n}{k} \frac{1}{s^{k}}. \end{align*} $$
The residue theorem gives
 $$ \begin{align*} \sum_{k=1}^{n}\binom{n}{k}\gamma_{Q}(k-1)=\frac{1}{2i\pi}\int_{C}k_{n}(s)\left(-\frac{Q'}{Q}(s+1,a)\right)ds, \end{align*} $$
$$ \begin{align*} \sum_{k=1}^{n}\binom{n}{k}\gamma_{Q}(k-1)=\frac{1}{2i\pi}\int_{C}k_{n}(s)\left(-\frac{Q'}{Q}(s+1,a)\right)ds, \end{align*} $$
where C is a contour enclosing the point
![]() $s = 0$
counterclockwise on a circle of small enough positive radius. The residue comes entirely from the singularity at
$s = 0$
counterclockwise on a circle of small enough positive radius. The residue comes entirely from the singularity at
![]() $s = 0$
, as no other singularities lie inside the contour. Let
$s = 0$
, as no other singularities lie inside the contour. Let
![]() $T=\sqrt {n}+\epsilon _{n}$
, for some
$T=\sqrt {n}+\epsilon _{n}$
, for some
![]() $0<\epsilon _{n}<1$
. Now we follow very closely the lines in [Reference Omar and Mazhouda16, pp. 1106–1107] using that the function
$0<\epsilon _{n}<1$
. Now we follow very closely the lines in [Reference Omar and Mazhouda16, pp. 1106–1107] using that the function
![]() $\frac {Q'}{Q}(s,a)$
satisfies the propertiesFootnote
1
$\frac {Q'}{Q}(s,a)$
satisfies the propertiesFootnote
1
 $$ \begin{align*} \frac{Q'}{Q}(s,a)=\sum_{\rho_a;\ |{\mathrm{Im}}(\rho_a -s)|<1}\frac{1}{s-\rho_{a}}+O(\log(1+|s|)), \end{align*} $$
$$ \begin{align*} \frac{Q'}{Q}(s,a)=\sum_{\rho_a;\ |{\mathrm{Im}}(\rho_a -s)|<1}\frac{1}{s-\rho_{a}}+O(\log(1+|s|)), \end{align*} $$
for
![]() $-2<\mathrm {Re}(s)<2$
and
$-2<\mathrm {Re}(s)<2$
and
 $$ \begin{align*} \left|\frac{Q'}{Q}(s+1,a)\right|=O(\log^{2}T), \end{align*} $$
$$ \begin{align*} \left|\frac{Q'}{Q}(s+1,a)\right|=O(\log^{2}T), \end{align*} $$
for
![]() $-2\leq \mathrm {Re}(s)\leq 2$
, and we get
$-2\leq \mathrm {Re}(s)\leq 2$
, and we get
 $$ \begin{align*} \sum_{k=1}^{n}\binom{n}{k}\gamma_{Q}(k-1)=\lambda_{-n,a,T}+O(\sqrt{n}\log n), \end{align*} $$
$$ \begin{align*} \sum_{k=1}^{n}\binom{n}{k}\gamma_{Q}(k-1)=\lambda_{-n,a,T}+O(\sqrt{n}\log n), \end{align*} $$
where
 $$ \begin{align*} \lambda_{-n,a,T}=\sum_{\rho_{a}\in{Z_{Q}};|Im (\rho_{a}|\leq T}^{*} \left(1-\left(1-\frac{1}{\rho_{a}}\right)^{n}\right), \end{align*} $$
$$ \begin{align*} \lambda_{-n,a,T}=\sum_{\rho_{a}\in{Z_{Q}};|Im (\rho_{a}|\leq T}^{*} \left(1-\left(1-\frac{1}{\rho_{a}}\right)^{n}\right), \end{align*} $$
with
![]() $T=\sqrt {n}+\epsilon _{n}$
. For
$T=\sqrt {n}+\epsilon _{n}$
. For
![]() $a=1/2,1/3,1/4,1/6$
, under the RH, since
$a=1/2,1/3,1/4,1/6$
, under the RH, since
![]() $\left |1-\frac {1}{\rho _{a}}\right |=1$
and using formula of
$\left |1-\frac {1}{\rho _{a}}\right |=1$
and using formula of
![]() $N_{Q}(T)$
given in Section 1.2, we obtain
$N_{Q}(T)$
given in Section 1.2, we obtain
![]() $\lambda _{n,a,T}=O(T\log T+1)$
. Therefore, Equation (2.5) follows from that
$\lambda _{n,a,T}=O(T\log T+1)$
. Therefore, Equation (2.5) follows from that
![]() $\lambda _{-n,a,\sqrt {n}}=\lambda _{-n,a,\sqrt {n}}=O(\sqrt {n}\log n)$
.
$\lambda _{-n,a,\sqrt {n}}=\lambda _{-n,a,\sqrt {n}}=O(\sqrt {n}\log n)$
.
Remark Since
![]() $2Q(s,a) := Z(s,a) + P(s,a)$
, from Corollary 2.3 below and [Reference Coffey6, Equation (1.18)], we obtain
$2Q(s,a) := Z(s,a) + P(s,a)$
, from Corollary 2.3 below and [Reference Coffey6, Equation (1.18)], we obtain
 $$ \begin{align*} \gamma_{Q}(n)=\frac{1}{2}\left(\delta_{n}(a)+\frac{(-1)^{n}}{n!}(l_{n}(a)+l_{n}(1-a))\right), \end{align*} $$
$$ \begin{align*} \gamma_{Q}(n)=\frac{1}{2}\left(\delta_{n}(a)+\frac{(-1)^{n}}{n!}(l_{n}(a)+l_{n}(1-a))\right), \end{align*} $$
where
![]() $\delta _n (a) = \frac {|\log a|^{n}}{an!} + O(1)$
and
$\delta _n (a) = \frac {|\log a|^{n}}{an!} + O(1)$
and
![]() $l_{n}(a)$
are the coefficients in the expansion of
$l_{n}(a)$
are the coefficients in the expansion of
![]() ${\mathrm {Li}}_s (e^{2\pi ia})$
at
${\mathrm {Li}}_s (e^{2\pi ia})$
at
![]() $s = 1$
; for
$s = 1$
; for
![]() $a\notin {\mathbb {Z}}$
, one has
$a\notin {\mathbb {Z}}$
, one has
 $$ \begin{align*} {\mathrm{Li}}_s (e^{2\pi ia})=\sum_{n=0}^{\infty}\frac{(-1)^{n}}{n!}l_{n}(a)(s-1)^{n}. \end{align*} $$
$$ \begin{align*} {\mathrm{Li}}_s (e^{2\pi ia})=\sum_{n=0}^{\infty}\frac{(-1)^{n}}{n!}l_{n}(a)(s-1)^{n}. \end{align*} $$
2.4 Proof of Theorem 1.4
To show Theorem 1.4, we quote the following lemmas from [Reference Apostol2, Reference Berndt3].
Lemma 2.1 [Reference Berndt3, Theorem 1]
We set
 $$\begin{align*}(s-1) \zeta (s,a) = 1+ \sum_{n=0}^\infty \gamma_n (a) (s-1)^{n+1}, \qquad 0 <a \le 1. \end{align*}$$
$$\begin{align*}(s-1) \zeta (s,a) = 1+ \sum_{n=0}^\infty \gamma_n (a) (s-1)^{n+1}, \qquad 0 <a \le 1. \end{align*}$$
Then it holds that
 $$\begin{align*}\gamma_n (a) = \frac{(-1)^n}{n!} \lim_{m \to \infty} \Biggl( \sum_{k=0}^m \frac{\log^n (k+a) }{k+a} - \frac{\log^{n+1} (m+a) }{n+1} \Biggr). \end{align*}$$
$$\begin{align*}\gamma_n (a) = \frac{(-1)^n}{n!} \lim_{m \to \infty} \Biggl( \sum_{k=0}^m \frac{\log^n (k+a) }{k+a} - \frac{\log^{n+1} (m+a) }{n+1} \Biggr). \end{align*}$$
Lemma 2.2 [Reference Apostol2, Equation (26)]
Let
![]() $0 < a \le 1$
, and let n be a nonnegative integer. Then one has
$0 < a \le 1$
, and let n be a nonnegative integer. Then one has
 $$ \begin{align*} \zeta^{(n)} (0,a) &= \biggl( \frac{1}{2} - a \biggr) |\log a|^n - n! + n! a \sum_{m=n}^\infty \frac{|\log a|^m }{m!}\\&\quad + (-1)^n n \int_0^\infty \frac{\varphi (x) \log^{n-1} (x+a)}{(x+a)^2} dx\\&\quad - (-1)^n n(n-1) \int_0^\infty \frac{\varphi (x) \log^{n-2} (x+a)}{(x+a)^2} dx,\end{align*} $$
$$ \begin{align*} \zeta^{(n)} (0,a) &= \biggl( \frac{1}{2} - a \biggr) |\log a|^n - n! + n! a \sum_{m=n}^\infty \frac{|\log a|^m }{m!}\\&\quad + (-1)^n n \int_0^\infty \frac{\varphi (x) \log^{n-1} (x+a)}{(x+a)^2} dx\\&\quad - (-1)^n n(n-1) \int_0^\infty \frac{\varphi (x) \log^{n-2} (x+a)}{(x+a)^2} dx,\end{align*} $$
where
![]() $\varphi (x) = \int _0^x (y- \lfloor y \rfloor - 1/2)dy$
is periodic with period
$\varphi (x) = \int _0^x (y- \lfloor y \rfloor - 1/2)dy$
is periodic with period
![]() $1$
and satisfies
$1$
and satisfies
![]() $2\varphi (x) = x(x-1)$
if
$2\varphi (x) = x(x-1)$
if
![]() $0 \le x \le 1$
.
$0 \le x \le 1$
.
By using the lemmas above, we immediately obtain the following.
Corollary 2.3 When
![]() $a>0$
is sufficiently small,
$a>0$
is sufficiently small,
 $$ \begin{align*} \begin{aligned} (s-1) Z(s,a) &= 2+ \sum_{n=0}^\infty \delta_n (a) (s-1)^{n+1}, \qquad \delta_n (a) = \frac{|\log a|^n}{an!} + O(1),\\ &Z(s,a) = \sum_{n=1}^\infty \epsilon_n (a) s^n, \qquad \epsilon_n (a) = O ( |\log a|^n ). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} (s-1) Z(s,a) &= 2+ \sum_{n=0}^\infty \delta_n (a) (s-1)^{n+1}, \qquad \delta_n (a) = \frac{|\log a|^n}{an!} + O(1),\\ &Z(s,a) = \sum_{n=1}^\infty \epsilon_n (a) s^n, \qquad \epsilon_n (a) = O ( |\log a|^n ). \end{aligned} \end{align*} $$
Proof The first formula and estimation are easily proved by Lemma 2.1 (see also [Reference Berndt3, Theorem 2]). For the first integral in Lemma 2.2, one has
 $$ \begin{align*} \begin{aligned} & \int_0^1 \frac{\varphi (x) \log^{n-1} (x+a)}{(x+a)^2} dx \ll \int_0^1 \frac{\log^{n-1} (x+a)}{x+a} dx = O ( |\log a|^n ), \\ & \int_1^\infty \frac{\varphi (x) \log^{n-1} (x+a)}{(x+a)^2} dx \ll \int_1^\infty \frac{\log^{n-1} (x+a)}{(x+a)^2} dx = O (1) \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} & \int_0^1 \frac{\varphi (x) \log^{n-1} (x+a)}{(x+a)^2} dx \ll \int_0^1 \frac{\log^{n-1} (x+a)}{x+a} dx = O ( |\log a|^n ), \\ & \int_1^\infty \frac{\varphi (x) \log^{n-1} (x+a)}{(x+a)^2} dx \ll \int_1^\infty \frac{\log^{n-1} (x+a)}{(x+a)^2} dx = O (1) \end{aligned} \end{align*} $$
from
![]() $x < x+a$
when
$x < x+a$
when
![]() $x,a>0$
. In addition, we have
$x,a>0$
. In addition, we have
 $$\begin{align*}a \sum_{m=n}^\infty \frac{|\log a|^m }{m!} \le a \sum_{m=0}^\infty \frac{|\log a|^m }{m!} = a e^{|\log a|} = a e^{-\log a} =1, \qquad 0< a <1/2. \end{align*}$$
$$\begin{align*}a \sum_{m=n}^\infty \frac{|\log a|^m }{m!} \le a \sum_{m=0}^\infty \frac{|\log a|^m }{m!} = a e^{|\log a|} = a e^{-\log a} =1, \qquad 0< a <1/2. \end{align*}$$
Hence, we obtain
 $$\begin{align*}\zeta (s,a) = \sum_{n=0}^\infty \frac{\zeta^{(n)} (0,a)}{n!} s^n, \qquad \zeta^{(n)} (0,a) = O ( |\log a|^n ). \end{align*}$$
$$\begin{align*}\zeta (s,a) = \sum_{n=0}^\infty \frac{\zeta^{(n)} (0,a)}{n!} s^n, \qquad \zeta^{(n)} (0,a) = O ( |\log a|^n ). \end{align*}$$
Therefore, we have
![]() $\epsilon _n (a) = O ( |\log a|^n )$
and the second formula in this corollary by the definition of
$\epsilon _n (a) = O ( |\log a|^n )$
and the second formula in this corollary by the definition of
![]() $Z(s,a)$
and
$Z(s,a)$
and
![]() $Z(0,a) = \zeta (0,a) +\zeta (0,1-a) = 0$
(see [Reference Nakamura15, Equation (4.11)]).
$Z(0,a) = \zeta (0,a) +\zeta (0,1-a) = 0$
(see [Reference Nakamura15, Equation (4.11)]).
Proof of Theorem 1.4
Recall the functional equation
(see [Reference Nakamura15, Lemma 4.11]). By using
![]() $\Gamma _{\!\! {\mathrm {cos}}} (s) \Gamma _{\!\! {\mathrm {cos}}} (1-s) =1$
, we have
$\Gamma _{\!\! {\mathrm {cos}}} (s) \Gamma _{\!\! {\mathrm {cos}}} (1-s) =1$
, we have
Let
![]() $|s-1|$
be sufficiently small. Then, by
$|s-1|$
be sufficiently small. Then, by
![]() $\lim _{s \to 1} (s-1) Q(s,a) = 1$
, the equation above, and the definitions of
$\lim _{s \to 1} (s-1) Q(s,a) = 1$
, the equation above, and the definitions of
![]() $Q(s,a)$
and
$Q(s,a)$
and
![]() $\xi _Q(s,a)$
, we have
$\xi _Q(s,a)$
, we have
 $$ \begin{align*} &\frac{d^l}{d s^l} \big[ s^{l-1} \log \xi_Q(s,a) \big]_{s=1} = \frac{d^l}{d s^l} \Big[ s^{l-1} \log \big( (s-1) Q(s,a) \big) + s^{l-1} \log \big( s \pi^{-s/2} \Gamma (s/2) \big) \Big]_{s=1} \\& \quad = \frac{d^l}{d s^l} \bigg[ s^{l-1} \log \bigg( \frac{s-1}{2} \Big( Z (s,a) + \Gamma_{\!\! {\mathrm{cos}}} (1-s) Z(1-s,a) \Big) \bigg) \bigg]_{s=1} + O_l(1) \\& \quad = \frac{d^l}{d s^l} \bigg[ s^{l-1} \log \bigg( 1 + \sum_{n=0}^\infty \Big( \delta_n^{\prime} (a) + \epsilon_n^{\prime} (a) \Big) (s-1)^{n+1} \bigg) \bigg]_{s=1} + O_l (1), \end{align*} $$
$$ \begin{align*} &\frac{d^l}{d s^l} \big[ s^{l-1} \log \xi_Q(s,a) \big]_{s=1} = \frac{d^l}{d s^l} \Big[ s^{l-1} \log \big( (s-1) Q(s,a) \big) + s^{l-1} \log \big( s \pi^{-s/2} \Gamma (s/2) \big) \Big]_{s=1} \\& \quad = \frac{d^l}{d s^l} \bigg[ s^{l-1} \log \bigg( \frac{s-1}{2} \Big( Z (s,a) + \Gamma_{\!\! {\mathrm{cos}}} (1-s) Z(1-s,a) \Big) \bigg) \bigg]_{s=1} + O_l(1) \\& \quad = \frac{d^l}{d s^l} \bigg[ s^{l-1} \log \bigg( 1 + \sum_{n=0}^\infty \Big( \delta_n^{\prime} (a) + \epsilon_n^{\prime} (a) \Big) (s-1)^{n+1} \bigg) \bigg]_{s=1} + O_l (1), \end{align*} $$
where
![]() $\delta _n^{\prime } (a)$
and
$\delta _n^{\prime } (a)$
and
![]() $\epsilon _n^{\prime } (a)$
are defined by
$\epsilon _n^{\prime } (a)$
are defined by
 $$\begin{align*}\delta_n^{\prime} (a) := \frac{\delta_n (a)}{2}, \qquad (s-1) \Gamma_{\!\! {\mathrm{cos}}} (1-s) Z(1-s,a) = 2 \sum_{n=0}^\infty \epsilon_n^{\prime} (a) (s-1)^{n+1}. \end{align*}$$
$$\begin{align*}\delta_n^{\prime} (a) := \frac{\delta_n (a)}{2}, \qquad (s-1) \Gamma_{\!\! {\mathrm{cos}}} (1-s) Z(1-s,a) = 2 \sum_{n=0}^\infty \epsilon_n^{\prime} (a) (s-1)^{n+1}. \end{align*}$$
Clearly, the second estimation in Corollary 2.3 implies
 $$\begin{align*}Z(1-s,a) = \sum_{n=1}^\infty \epsilon_n (a) (1-s)^n,\qquad \epsilon_n (a) = O ( |\log a|^n ). \end{align*}$$
$$\begin{align*}Z(1-s,a) = \sum_{n=1}^\infty \epsilon_n (a) (1-s)^n,\qquad \epsilon_n (a) = O ( |\log a|^n ). \end{align*}$$
Thus, we can see that
![]() $\epsilon _n^{\prime } (a) = O ( |\log a|^{n+1} )$
from
$\epsilon _n^{\prime } (a) = O ( |\log a|^{n+1} )$
from
![]() $\lim _{s \to 1} (s-1) \Gamma _{\!\! {\mathrm {cos}}} (1-s) = -2$
and the fact that the function
$\lim _{s \to 1} (s-1) \Gamma _{\!\! {\mathrm {cos}}} (1-s) = -2$
and the fact that the function
![]() $(s-1) \Gamma _{\!\! {\mathrm {cos}}} (1-s)$
does not depend on a. Put
$(s-1) \Gamma _{\!\! {\mathrm {cos}}} (1-s)$
does not depend on a. Put
![]() $\eta _n(a) := \delta _n^{\prime } (a) + \epsilon _n^{\prime } (a)$
. Then, for
$\eta _n(a) := \delta _n^{\prime } (a) + \epsilon _n^{\prime } (a)$
. Then, for
![]() $n \ge 0$
, we have
$n \ge 0$
, we have
by Corollary 2.3. By virtue of
 $$ \begin{align*} \begin{aligned} (a_0 x + a_1 x^2 + a_2 x^3 + \cdots)^m = a_0^m & x^m + \binom{m}{1} a_0^{m-1 }a_1 x^{m+1} + \cdots \\ (a_0 x + a_1 x^2 + a_2 x^3 + \cdots)^{m-1} = a_0^m x^{m-1} + \binom{m-1}{1} a_0^{m-2} a_1 & x^{m} + \cdots \\ & \vdots \\ (a_0 x + a_1 x^2 + a_2 x^3 + \cdots)^{1} = \cdots + a_m & x^m + \cdots, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} (a_0 x + a_1 x^2 + a_2 x^3 + \cdots)^m = a_0^m & x^m + \binom{m}{1} a_0^{m-1 }a_1 x^{m+1} + \cdots \\ (a_0 x + a_1 x^2 + a_2 x^3 + \cdots)^{m-1} = a_0^m x^{m-1} + \binom{m-1}{1} a_0^{m-2} a_1 & x^{m} + \cdots \\ & \vdots \\ (a_0 x + a_1 x^2 + a_2 x^3 + \cdots)^{1} = \cdots + a_m & x^m + \cdots, \end{aligned} \end{align*} $$
where
![]() $m \in {\mathbb {N}}$
and
$m \in {\mathbb {N}}$
and
![]() $a_m,x \in {\mathbb {C}}$
, the coefficient of
$a_m,x \in {\mathbb {C}}$
, the coefficient of
![]() $(s-1)^l$
in the function
$(s-1)^l$
in the function
 $$\begin{align*}f(s,a) := \sum_{m=1}^\infty \frac{(-1)^{m+1}}{m} \Biggl( \sum_{n=0}^\infty \eta_n(a) (s-1)^{n+1} \Biggr)^{\!\!\!m} \end{align*}$$
$$\begin{align*}f(s,a) := \sum_{m=1}^\infty \frac{(-1)^{m+1}}{m} \Biggl( \sum_{n=0}^\infty \eta_n(a) (s-1)^{n+1} \Biggr)^{\!\!\!m} \end{align*}$$
is expressed as
Note that the function above is estimated by
from (2.6) when
![]() $a \to +0$
. We can find that
$a \to +0$
. We can find that
 $$\begin{align*}(s-1) \Bigl( Z (s,a) + \Gamma_{\!\! {\mathrm{cos}}} (1-s) Z(1-s,a) \Bigr) = 1 + \sum_{n=0}^\infty \eta_n (a) (s-1)^{n+1} \end{align*}$$
$$\begin{align*}(s-1) \Bigl( Z (s,a) + \Gamma_{\!\! {\mathrm{cos}}} (1-s) Z(1-s,a) \Bigr) = 1 + \sum_{n=0}^\infty \eta_n (a) (s-1)^{n+1} \end{align*}$$
is analytic when
![]() $|s-1|<1$
form the poles of
$|s-1|<1$
form the poles of
![]() $Z (s,a)$
and
$Z (s,a)$
and
![]() $\Gamma _{\!\! {\mathrm {cos}}} (1-s)$
. So we can choose
$\Gamma _{\!\! {\mathrm {cos}}} (1-s)$
. So we can choose
![]() $|s-1|>0$
such that
$|s-1|>0$
such that
 $$\begin{align*}\sum_{n=0}^\infty \bigl|\eta_n (a) \bigr| |s-1|^{n+1} < \frac{1}{2}. \end{align*}$$
$$\begin{align*}\sum_{n=0}^\infty \bigl|\eta_n (a) \bigr| |s-1|^{n+1} < \frac{1}{2}. \end{align*}$$
Then, from (2.7), the Leibniz product rule, the definition of
![]() $\eta _n(a)$
, and the Taylor expansion of
$\eta _n(a)$
, and the Taylor expansion of
![]() $\log (1+x)$
with
$\log (1+x)$
with
![]() $|x| <1$
, one has
$|x| <1$
, one has
 $$ \begin{align} &\frac{d^l}{d s^l} \Bigl[ s^{l-1} \log \xi_Q(s,a) \Bigr]_{s=1} = \frac{d^l}{d s^l} \Bigl[ s^{l-1} f (s,a) \Bigr]_{s=1} + O_l (1) \notag\\& \quad = \binom{l}{l} \frac{(-1)^{l+1}}{l} l! \bigl( \eta_0 (a) \bigr)^l + O_l \bigl( \eta_0 (a)^{l-2} \eta_1 (a) \bigr)\end{align} $$
$$ \begin{align} &\frac{d^l}{d s^l} \Bigl[ s^{l-1} \log \xi_Q(s,a) \Bigr]_{s=1} = \frac{d^l}{d s^l} \Bigl[ s^{l-1} f (s,a) \Bigr]_{s=1} + O_l (1) \notag\\& \quad = \binom{l}{l} \frac{(-1)^{l+1}}{l} l! \bigl( \eta_0 (a) \bigr)^l + O_l \bigl( \eta_0 (a)^{l-2} \eta_1 (a) \bigr)\end{align} $$
Note that (
![]() $\flat $
) comes from
$\flat $
) comes from
![]() $f^{(l)} (s,a)$
, (
$f^{(l)} (s,a)$
, (
![]() $\natural $
) is deduced by
$\natural $
) is deduced by
![]() $f^{(l-1)} (s,a)$
, and (
$f^{(l-1)} (s,a)$
, and (
![]() $\sharp $
) derives from
$\sharp $
) derives from
![]() $f^{(1)} (s,a)$
,
$f^{(1)} (s,a)$
,
![]() $f^{(0)} (s,a)$
, and
$f^{(0)} (s,a)$
, and
![]() $O_l (1)$
in the left-hand side of the formula above. Therefore, by (2.8), we obtain
$O_l (1)$
in the left-hand side of the formula above. Therefore, by (2.8), we obtain
 $$ \begin{align*} \begin{split} \frac{d^l}{d s^l} \Bigl[ s^{l-1} \log \xi_Q(s,a) \Bigr]_{s=1} &= (-1)^{l+1} (l-1)! \bigl( \eta_0 (a) \bigr)^l + O_l \bigl( \eta_0 (a)^{l-2} \eta_1 (a) \bigr) \\ &= (-1)^{l+1} \frac{(l-1)!}{(2a)^l} + O_l \bigl(a^{1-l} |\log a| \bigr), \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \frac{d^l}{d s^l} \Bigl[ s^{l-1} \log \xi_Q(s,a) \Bigr]_{s=1} &= (-1)^{l+1} (l-1)! \bigl( \eta_0 (a) \bigr)^l + O_l \bigl( \eta_0 (a)^{l-2} \eta_1 (a) \bigr) \\ &= (-1)^{l+1} \frac{(l-1)!}{(2a)^l} + O_l \bigl(a^{1-l} |\log a| \bigr), \end{split} \end{align*} $$
which implies Theorem 1.4.
At the end of the paper, we give numerical computation for
![]() $\lambda _{n,a}$
by Mathematica 13.0. Let
$\lambda _{n,a}$
by Mathematica 13.0. Let
 $$\begin{align*}\lambda_{n,a}^{[k]} := \frac{1}{(n-1)!} \frac{d^n}{d s^n} \bigl[ s^{n-1} \log \xi_Q(s,a) \bigr]_{s=1-10^{-k}}, \qquad \lambda_{n,a}^* := \frac{(-1)^{n+1}}{(2a)^n}. \end{align*}$$
$$\begin{align*}\lambda_{n,a}^{[k]} := \frac{1}{(n-1)!} \frac{d^n}{d s^n} \bigl[ s^{n-1} \log \xi_Q(s,a) \bigr]_{s=1-10^{-k}}, \qquad \lambda_{n,a}^* := \frac{(-1)^{n+1}}{(2a)^n}. \end{align*}$$
Then, we have the following.
For
![]() $n=1$
, we have
$n=1$
, we have
 $$ \begin{align*}\begin{array}{ccrll} a := 2^{-17}& \lambda_{1,a}^{[10]} = 65,537... & \lambda_{1,a}^{[10]} / \lambda_{1,a}^* = 1.00001...\\ a := 2^{-18}& \lambda_{1,a}^{[10]} = 131,074... & \lambda_{1,a}^{[10]} / \lambda_{1,a}^* = 1.00002...\\ a := 2^{-19}& \lambda_{1,a}^{[10]} = 262,151... & \lambda_{1,a}^{[10]} / \lambda_{1,a}^* = 1.00003...\\ a := 2^{-17}& \lambda_{1,a}^{[11]} = 65,536.6... & \lambda_{1,a}^{[11]} / \lambda_{1,a}^* = 1.00001...\\ a := 2^{-18}& \lambda_{1,a}^{[11]} = 131,073... & \lambda_{1,a}^{[11]} / \lambda_{1,a}^* = 1.00001...\\ a := 2^{-19}& \lambda_{1,a}^{[11]} = 262,145... & \lambda_{1,a}^{[11]} / \lambda_{1,a}^* = 1.00000...\\ a := 2^{-17}& \lambda_{1,a}^{[12]} = 655,365... & \lambda_{1,a}^{[12]} / \lambda_{1,a}^* = 1.00001...\\ a := 2^{-18}& \lambda_{1,a}^{[12]} = 131,073... & \lambda_{1,a}^{[12]} / \lambda_{1,a}^* = 1.00000...\\ a := 2^{-19}& \lambda_{1,a}^{[12]} = 262,145... & \lambda_{1,a}^{[12]} / \lambda_{1,a}^* = 1.00000... \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{ccrll} a := 2^{-17}& \lambda_{1,a}^{[10]} = 65,537... & \lambda_{1,a}^{[10]} / \lambda_{1,a}^* = 1.00001...\\ a := 2^{-18}& \lambda_{1,a}^{[10]} = 131,074... & \lambda_{1,a}^{[10]} / \lambda_{1,a}^* = 1.00002...\\ a := 2^{-19}& \lambda_{1,a}^{[10]} = 262,151... & \lambda_{1,a}^{[10]} / \lambda_{1,a}^* = 1.00003...\\ a := 2^{-17}& \lambda_{1,a}^{[11]} = 65,536.6... & \lambda_{1,a}^{[11]} / \lambda_{1,a}^* = 1.00001...\\ a := 2^{-18}& \lambda_{1,a}^{[11]} = 131,073... & \lambda_{1,a}^{[11]} / \lambda_{1,a}^* = 1.00001...\\ a := 2^{-19}& \lambda_{1,a}^{[11]} = 262,145... & \lambda_{1,a}^{[11]} / \lambda_{1,a}^* = 1.00000...\\ a := 2^{-17}& \lambda_{1,a}^{[12]} = 655,365... & \lambda_{1,a}^{[12]} / \lambda_{1,a}^* = 1.00001...\\ a := 2^{-18}& \lambda_{1,a}^{[12]} = 131,073... & \lambda_{1,a}^{[12]} / \lambda_{1,a}^* = 1.00000...\\ a := 2^{-19}& \lambda_{1,a}^{[12]} = 262,145... & \lambda_{1,a}^{[12]} / \lambda_{1,a}^* = 1.00000... \end{array}\end{align*} $$
For
![]() $n=2$
, we have
$n=2$
, we have
 $$ \begin{align*}\begin{array}{ccrll} a := 2^{-17}&\ \ \ \ \ \ \lambda_{2,a}^{[10]} = -4.29352... \times 10^9 & \ \ \ \ \ \ \lambda_{2,a}^{[10]} / \lambda_{2,a}^* = 0.999663...\\ a := 2^{-18}& \ \ \ \ \ \ \lambda_{2,a}^{[10]} = -1.7177... \times 10^{10}&\ \ \ \ \ \ \lambda_{2,a}^{[10]} / \lambda_{2,a}^* = 0.999836...\\ a := 2^{-19}&\ \ \ \ \ \ \lambda_{2,a}^{[10]} = -6.87162... \times 10^{10}& \ \ \ \ \ \ \lambda_{2,a}^{[10]} / \lambda_{2,a}^* = 0.999952...\\ a := 2^{-17}&\ \ \ \ \ \ \lambda_{2,a}^{[11]} = -4.29478... \times 10^9&\ \ \ \ \ \ \lambda_{2,a}^{[11]} / \lambda_{2,a}^* = 0.999956...\\ a := 2^{-18}&\ \ \ \ \ \ \lambda_{2,a}^{[11]} = -1.71753... \times 10^{10}&\ \ \ \ \ \ \lambda_{2,a}^{[11]} / \lambda_{2,a}^* = 0.999736...\\ a := 2^{-19}&\ \ \ \ \ \ \lambda_{2,a}^{[11]} = -6.87149... \times 10^{10}& \ \ \ \ \ \ \lambda_{2,a}^{[11]} / \lambda_{2,a}^* = 0.999933...\\ a := 2^{-17}&\ \ \ \ \ \ \lambda_{2,a}^{[12]} = -4.29477... \times 10^9& \ \ \ \ \ \ \lambda_{2,a}^{[12]} / \lambda_{2,a}^* = 0.999955...\\ a := 2^{-18}& \ \ \ \ \ \ \lambda_{2,a}^{[12]} = -1.6911... \times 10^{10}&\ \ \ \ \ \ \lambda_{2,a}^{[12]} / \lambda_{2,a}^* = 0.984353...\\ a := 2^{-19}&\ \ \ \ \ \ \lambda_{2,a}^{[12]} = -6.87187... \times 10^{10}& \ \ \ \ \ \ \lambda_{2,a}^{[12]} / \lambda_{2,a}^* = 0.999989... \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ccrll} a := 2^{-17}&\ \ \ \ \ \ \lambda_{2,a}^{[10]} = -4.29352... \times 10^9 & \ \ \ \ \ \ \lambda_{2,a}^{[10]} / \lambda_{2,a}^* = 0.999663...\\ a := 2^{-18}& \ \ \ \ \ \ \lambda_{2,a}^{[10]} = -1.7177... \times 10^{10}&\ \ \ \ \ \ \lambda_{2,a}^{[10]} / \lambda_{2,a}^* = 0.999836...\\ a := 2^{-19}&\ \ \ \ \ \ \lambda_{2,a}^{[10]} = -6.87162... \times 10^{10}& \ \ \ \ \ \ \lambda_{2,a}^{[10]} / \lambda_{2,a}^* = 0.999952...\\ a := 2^{-17}&\ \ \ \ \ \ \lambda_{2,a}^{[11]} = -4.29478... \times 10^9&\ \ \ \ \ \ \lambda_{2,a}^{[11]} / \lambda_{2,a}^* = 0.999956...\\ a := 2^{-18}&\ \ \ \ \ \ \lambda_{2,a}^{[11]} = -1.71753... \times 10^{10}&\ \ \ \ \ \ \lambda_{2,a}^{[11]} / \lambda_{2,a}^* = 0.999736...\\ a := 2^{-19}&\ \ \ \ \ \ \lambda_{2,a}^{[11]} = -6.87149... \times 10^{10}& \ \ \ \ \ \ \lambda_{2,a}^{[11]} / \lambda_{2,a}^* = 0.999933...\\ a := 2^{-17}&\ \ \ \ \ \ \lambda_{2,a}^{[12]} = -4.29477... \times 10^9& \ \ \ \ \ \ \lambda_{2,a}^{[12]} / \lambda_{2,a}^* = 0.999955...\\ a := 2^{-18}& \ \ \ \ \ \ \lambda_{2,a}^{[12]} = -1.6911... \times 10^{10}&\ \ \ \ \ \ \lambda_{2,a}^{[12]} / \lambda_{2,a}^* = 0.984353...\\ a := 2^{-19}&\ \ \ \ \ \ \lambda_{2,a}^{[12]} = -6.87187... \times 10^{10}& \ \ \ \ \ \ \lambda_{2,a}^{[12]} / \lambda_{2,a}^* = 0.999989... \end{array} \end{align*} $$
Acknowledgements
The authors want to thank the anonymous referees for their many insightful comments and suggestions.