Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-24T00:53:03.927Z Has data issue: false hasContentIssue false
  • English
  • Français

Isomorphisms of Function Algebras and Algebras of Analytic Functions

Published online by Cambridge University Press:  20 November 2018

Bruce Lund
Bruce Lund*
Affiliation:
Department of Mathematics, University of New Brunswick,Fredericton, N. B., Canada
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be a finite open Riemann surface with analytic boundary Γ. Set 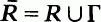and define 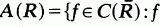is analytic on R}. Conditions are given on a function algebra A on a compact Hausdorff space X which imply that A is isomorphic to a subalgebra of A(R) of finite codimension.

Keywords

46J10function algebraGleason partf-regular
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 21 , Issue 1 , 01 March 1978 , pp. 61 - 71
Copyright
Copyright © Canadian Mathematical Society 1978

References

1. Ahlfors, L. and Sario, L., Riemann surfaces Princeton University Press, Princeton, N.J., 1960.Google Scholar
2. Arens, R., The closed maximal ideals of algebras of functions holomorphic on a Riemann surface, Rend. Cir. Mat. di Palermo (2) 7 (1958), 245-260.Google Scholar
3. Björk, J.-E., Analytic structures, Papers from the Summer Gathering on Functional Algebras at Aarhus July (1969), 19-28.Google Scholar
4. Björk, J.-E., On analytic structure in the maximal ideal space of a function algebra, Papers from the Summer Gathering on Function Algebras at Aarhus July (1969), 29-35.Google Scholar
5. Browder, A., Introduction to function algebras W. A. Benjamin, New York, 1969.Google Scholar
6. Duren, P. L., Theory of Hp spaces Academic Press, New York, 1970.Google Scholar
7. Gamelin, T. W., Embedding Riemann surfaces in maximal ideal spaces, J. Functional Analysis 2 (1968), 123-146.Google Scholar
8. Gamelin, T. W., Uniform algebras Prentice-Hall, Englewood Cliffs, N.J., 1969.Google Scholar
9. Gamelin, T. W., Polynomial approximation on thin sets, Symposium on Several Complex Variables Park City, Utah (1970), Lecture notes in mathematics 184, Springer Verlag, Berlin, 1971.Google Scholar
10. Gamelin, T. W. and Lumer, G., Abstract Hardy spaces and universal Hardy class, Advances in Math. 2 (1968), 118-174.Google Scholar
11. Kiski, K., Homeomorphism between the open unit disk and a Gleason part, J. Math. Soc. Japan 27 (1975), 467-473.Google Scholar
12. Lund, B., Subalgebras of finite codimension in the algebra on analytic functions on a Riemann surface, Pacific J. Math. 51 (1974), 495-497.Google Scholar
13. Lund, B., Analytic embeddings in logmodular algebras, Indiana Univ. Math. J. 24 (1975), 1093-1098.Google Scholar
14. Munkres, J. R., Topology Prentice-Hall, Englewood Cliffs, N.J., 1975.Google Scholar
15. Read, A., A converse of Cauchy's theorem and applications to extremal problems, Acta Math. 100 (1958), 1-22.Google Scholar
16. Stanton, C. M., The closed ideals of a function algebra, Trans, Amer. Math. Soc. 154 (1971), 289-300.Google Scholar
17. Stout, E. L., On some algebras of analytic functions on finite open Riemann surfaces, Math. Z. 92 (1966), 366-379.Google Scholar
18. Stout, E. L., The theory of uniform algebras Bogden and Quigley, Tarrytown-on-Hudson, N.Y., 1971.Google Scholar