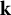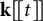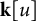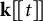1 Introduction
It is well-known that the normalization of a curve X is a non-singular curve Y. Serre considers in [Reference Serre26, Chapter IV] the opposite direction, he showed how to construct a curve X from a given non-singular curve Y such that this curve is the normalization of X. This idea appears in several different contexts. For instance, in [Reference Gorin17, Reference Grönkvist, Leffler, Torstensson and Ufnarovski18, Reference Newman23] and the references therein, is studied how to determine the finite codimension sub-
![]() ${\mathbf {k}}$
-algebras B of
${\mathbf {k}}$
-algebras B of
![]() ${\mathbf {k}}[t]$
. Notice that, in this case,
${\mathbf {k}}[t]$
. Notice that, in this case,
![]() $X=\operatorname {Spec}(B)$
is an algebraic curve and the affine line
$X=\operatorname {Spec}(B)$
is an algebraic curve and the affine line
![]() $Y=\operatorname {Spec}({\mathbf {k}}[t])$
is its normalization. These sub-algebras are defined recursively on the codimension by linear and higher differential conditions. Only for low codimensions, explicit conditions are known. Since not all higher differential conditions define sub-algebras of
$Y=\operatorname {Spec}({\mathbf {k}}[t])$
is its normalization. These sub-algebras are defined recursively on the codimension by linear and higher differential conditions. Only for low codimensions, explicit conditions are known. Since not all higher differential conditions define sub-algebras of
![]() ${\mathbf {k}}[t]$
, it is an open problem for the characterization of families of linear higher differential operators defining finite codimension sub-
${\mathbf {k}}[t]$
, it is an open problem for the characterization of families of linear higher differential operators defining finite codimension sub-
![]() ${\mathbf {k}}$
-algebras of
${\mathbf {k}}$
-algebras of
![]() ${\mathbf {k}}[t]$
(see [Reference Grönkvist, Leffler, Torstensson and Ufnarovski18]).
${\mathbf {k}}[t]$
(see [Reference Grönkvist, Leffler, Torstensson and Ufnarovski18]).
In the search of one-dimensional reduced local rings with locally decreasing Hilbert function, Roberts constructed such a local rings as connex, finite codimension sub-
![]() ${\mathbf {k}}$
-algebras of
${\mathbf {k}}$
-algebras of
![]() $\prod _{i=1}^r {\mathbf {k}}[t_i]$
defined by linear and first-order differentials conditions (see [Reference Gupta and Roberts19]). See [Reference Elias11] for the proof of Sally’s conjecture on the monotony of Hilbert functions of one-dimensional Cohen–Macaulay local rings.
$\prod _{i=1}^r {\mathbf {k}}[t_i]$
defined by linear and first-order differentials conditions (see [Reference Gupta and Roberts19]). See [Reference Elias11] for the proof of Sally’s conjecture on the monotony of Hilbert functions of one-dimensional Cohen–Macaulay local rings.
In this paper, we consider the local complete case. We characterize the finite codimension sub-
![]() ${\mathbf {k}}$
-algebras B of
${\mathbf {k}}$
-algebras B of
![]() $\Gamma ={\mathbf {k}}[\![t]\!]$
as the solutions of a computable finite codimension
$\Gamma ={\mathbf {k}}[\![t]\!]$
as the solutions of a computable finite codimension
![]() ${\mathbf {k}}$
-vector space
${\mathbf {k}}$
-vector space
![]() $B^{\perp }\subset \Delta ={\mathbf {k}}[u]$
of higher differential operators (see Theorem 3.9). For this purpose, we establish a Macaulay-like duality between finite codimension sub-
$B^{\perp }\subset \Delta ={\mathbf {k}}[u]$
of higher differential operators (see Theorem 3.9). For this purpose, we establish a Macaulay-like duality between finite codimension sub-
![]() ${\mathbf {k}}$
-algebras B of
${\mathbf {k}}$
-algebras B of
![]() $\Gamma $
and finite codimension
$\Gamma $
and finite codimension
![]() ${\mathbf {k}}$
-vector subspaces
${\mathbf {k}}$
-vector subspaces
![]() $B^{\perp }$
, so-called algebra-forming vector spaces, of the polynomial ring
$B^{\perp }$
, so-called algebra-forming vector spaces, of the polynomial ring
![]() $\Delta $
. The polynomial ring
$\Delta $
. The polynomial ring
![]() $\Delta $
acts on
$\Delta $
acts on
![]() $\Gamma $
by differentiation as in Macaulay’s duality (see [Reference Elias, Cuong, Hoa and Trung14–Reference Elias and Rossi16, Reference Iarrobino and Kanev20]). At the end of Section 3, we describe the linear maps
$\Gamma $
by differentiation as in Macaulay’s duality (see [Reference Elias, Cuong, Hoa and Trung14–Reference Elias and Rossi16, Reference Iarrobino and Kanev20]). At the end of Section 3, we describe the linear maps
![]() $B_2^{\perp }\rightarrow B_1^{\perp }$
induced by
$B_2^{\perp }\rightarrow B_1^{\perp }$
induced by
![]() ${\mathbf {k}}$
-algebra morphisms
${\mathbf {k}}$
-algebra morphisms
![]() $B_1\rightarrow B_2$
between two finite codimension
$B_1\rightarrow B_2$
between two finite codimension
![]() ${\mathbf {k}}$
-algebras
${\mathbf {k}}$
-algebras
![]() $B_1$
,
$B_1$
,
![]() $B_2$
.
$B_2$
.
In Section 4, we study the algebra-forming vector spaces, showing that such a condition can be checked effectively (see Proposition 4.1). After this, we prove that for any finite codimension
![]() $\delta $
$\delta $
![]() ${\mathbf {k}}$
-algebra B there exist a finite filtration of
${\mathbf {k}}$
-algebra B there exist a finite filtration of
![]() ${\mathbf {k}}$
-algebras, so-called standard filtration of B,
${\mathbf {k}}$
-algebras, so-called standard filtration of B,
![]() $B=B_0\subset B_1\subset \cdots \subset B_{\delta }=\Gamma $
such that
$B=B_0\subset B_1\subset \cdots \subset B_{\delta }=\Gamma $
such that
![]() $\operatorname {dim}_{{\mathbf {k}}}(B_{i+1}/B_i)=1$
for
$\operatorname {dim}_{{\mathbf {k}}}(B_{i+1}/B_i)=1$
for
![]() $i=0,\dots ,\delta -1$
. As corollary of this construction, we get that we only need to consider algebra-forming single elements in order to define recursively a finite codimension
$i=0,\dots ,\delta -1$
. As corollary of this construction, we get that we only need to consider algebra-forming single elements in order to define recursively a finite codimension
![]() ${\mathbf {k}}$
-algebras. Moreover, we show how to recover the standard filtration by considering recursively derivations of the local rings appearing in the filtration (see Corollary 4.6).
${\mathbf {k}}$
-algebras. Moreover, we show how to recover the standard filtration by considering recursively derivations of the local rings appearing in the filtration (see Corollary 4.6).
Section 5 is devoted to study the inverse system of monomial
![]() ${\mathbf {k}}$
-algebras and the special case of monomial Gorenstein algebras. We end the section relating the inverse system of a curve singularity with its generic plane projection and its saturation.
${\mathbf {k}}$
-algebras and the special case of monomial Gorenstein algebras. We end the section relating the inverse system of a curve singularity with its generic plane projection and its saturation.
In the last section, we link
![]() $B^{\perp }$
with the canonical module of B (see Proposition 6.1).
$B^{\perp }$
with the canonical module of B (see Proposition 6.1).
The computations of this paper are performed by using the computer algebra system singular (see [Reference Decker, Greuel, Pfister and Schönemann8]).
2 Preliminaries
Let R denote the power series ring
![]() $ {\mathbf {k}}[\![x_1, \dots , x_n]\!] $
over an algebraically closed characteristic zero field
$ {\mathbf {k}}[\![x_1, \dots , x_n]\!] $
over an algebraically closed characteristic zero field
![]() ${\mathbf {k}}$
and we denote by
${\mathbf {k}}$
and we denote by
![]() $\max =(x_1,\dots , x_n)$
its maximal ideal.
$\max =(x_1,\dots , x_n)$
its maximal ideal.
Let A be a one-dimensional local ring with maximal ideal
![]() $\max $
. We denote by
$\max $
. We denote by
![]() ${\operatorname {H\!F}}_A$
the Hilbert function of A, i.e.,
${\operatorname {H\!F}}_A$
the Hilbert function of A, i.e.,
![]() ${\operatorname {H\!F}}_A(i)=\operatorname {Length}_A(\max ^i/\max ^{i+1})$
,
${\operatorname {H\!F}}_A(i)=\operatorname {Length}_A(\max ^i/\max ^{i+1})$
,
![]() $i\ge 0$
. It is well-known that
$i\ge 0$
. It is well-known that
![]() ${\operatorname {H\!F}}^0_A(i)=e_0(A)$
,
${\operatorname {H\!F}}^0_A(i)=e_0(A)$
,
![]() $i\gg 0$
, where
$i\gg 0$
, where
![]() $e_0(A)$
is the multiplicity of A. The first integral of
$e_0(A)$
is the multiplicity of A. The first integral of
![]() ${\operatorname {H\!F}}_A$
is defined by,
${\operatorname {H\!F}}_A$
is defined by,
![]() $i\ge 0$
,
$i\ge 0$
,
 $$ \begin{align*}{\operatorname{H\!F}}^1_A(i)=\sum_{j=0}^i {\operatorname{H\!F}}_A(j)= \operatorname{Length}_A(A/{\max}^{i+1}).\end{align*} $$
$$ \begin{align*}{\operatorname{H\!F}}^1_A(i)=\sum_{j=0}^i {\operatorname{H\!F}}_A(j)= \operatorname{Length}_A(A/{\max}^{i+1}).\end{align*} $$
We write
![]() ${\operatorname {H\!F}}_A^0={\operatorname {H\!F}}_A$
. There exists an integer
${\operatorname {H\!F}}_A^0={\operatorname {H\!F}}_A$
. There exists an integer
![]() $e_1(A)$
such that
$e_1(A)$
such that
![]() ${\operatorname {H\!F}}^1_A(i)=e_0(A)( i+1) -e_1(A)$
for
${\operatorname {H\!F}}^1_A(i)=e_0(A)( i+1) -e_1(A)$
for
![]() $i\gg 0$
; the (first) Hilbert polynomial is
$i\gg 0$
; the (first) Hilbert polynomial is
![]() $\operatorname {H\!P}^1_A(T)=e_0(A)( T+1) -e_1(A)$
. See [Reference Matlis22, Chapter XII] for the basic properties of the Hilbert functions of one-dimensional Cohen–Macaulay local rings.
$\operatorname {H\!P}^1_A(T)=e_0(A)( T+1) -e_1(A)$
. See [Reference Matlis22, Chapter XII] for the basic properties of the Hilbert functions of one-dimensional Cohen–Macaulay local rings.
A branch X is an irreducible curve singularity of
![]() $({\mathbf {k}}^n,0)=\operatorname {Spec}(R)$
, i.e., X is a one-dimensional, integral scheme
$({\mathbf {k}}^n,0)=\operatorname {Spec}(R)$
, i.e., X is a one-dimensional, integral scheme
![]() $X=\operatorname {Spec}(R/I)$
; we write
$X=\operatorname {Spec}(R/I)$
; we write
![]() ${\mathcal O}_{X}=R/I$
and
${\mathcal O}_{X}=R/I$
and
![]() $I(X)=I$
.
$I(X)=I$
.
Let
![]() $\nu : \overline {X}=\operatorname {Spec} (\overline {{\mathcal O}_{X}})\longrightarrow (X,0)$
be the normalization of
$\nu : \overline {X}=\operatorname {Spec} (\overline {{\mathcal O}_{X}})\longrightarrow (X,0)$
be the normalization of
![]() $(X,0)$
, where
$(X,0)$
, where
![]() $\overline {{\mathcal O}_{X}}\cong {\mathbf {k}}[\![t]\!]$
is the integral closure of
$\overline {{\mathcal O}_{X}}\cong {\mathbf {k}}[\![t]\!]$
is the integral closure of
![]() ${\mathcal O}_{X}$
on its full field of fractions
${\mathcal O}_{X}$
on its full field of fractions
![]() ${\mathrm { tot}}({\mathcal O}_{X})$
. The singularity order of X is
${\mathrm { tot}}({\mathcal O}_{X})$
. The singularity order of X is
![]() $ \delta (X)=\operatorname {dim}_{{\mathbf {k}}}\left ({\mathcal O}_{\overline {X}}/{\mathcal O}_{X}\right ). $
We denote by
$ \delta (X)=\operatorname {dim}_{{\mathbf {k}}}\left ({\mathcal O}_{\overline {X}}/{\mathcal O}_{X}\right ). $
We denote by
![]() $\mathcal C$
the conductor of the finite extension
$\mathcal C$
the conductor of the finite extension
![]() $\nu ^*: {\mathcal O}_{X} \hookrightarrow \overline {{\mathcal O}_{X}}$
and by
$\nu ^*: {\mathcal O}_{X} \hookrightarrow \overline {{\mathcal O}_{X}}$
and by
![]() $c(X)$
the dimension of
$c(X)$
the dimension of
![]() $\overline {{\mathcal O}_{X}}/\mathcal C$
.
$\overline {{\mathcal O}_{X}}/\mathcal C$
.
Given a set of nonnegative integers
![]() $1\le a_1<\cdots <a_n$
, we consider the monomial curve singularity
$1\le a_1<\cdots <a_n$
, we consider the monomial curve singularity
![]() $X(a_1,\dots , a_n)$
defined by the parameterization
$X(a_1,\dots , a_n)$
defined by the parameterization
i.e.,
![]() $I(X(a_1,\dots , a_n))=\ker (\gamma )$
. If
$I(X(a_1,\dots , a_n))=\ker (\gamma )$
. If
![]() $gcd(a_1,\dots , a_n)=1,$
then the induced map
$gcd(a_1,\dots , a_n)=1,$
then the induced map
is the normalization map of
![]() $\mathcal O_{X(a_1,\dots , a_n)}=R/I(X(a_1,\dots , a_n))={\mathbf {k}}[\![t^{a_1},\dots , t^{a_n}]\!]$
.
$\mathcal O_{X(a_1,\dots , a_n)}=R/I(X(a_1,\dots , a_n))={\mathbf {k}}[\![t^{a_1},\dots , t^{a_n}]\!]$
.
We denote by
![]() $D_X$
the semigroup of values of X: the set of integers
$D_X$
the semigroup of values of X: the set of integers
![]() $v_t(f)=ord_t(t)$
where
$v_t(f)=ord_t(t)$
where
![]() $f\in {\mathcal O}_{X}\setminus \{0\}$
. It is easy to see that
$f\in {\mathcal O}_{X}\setminus \{0\}$
. It is easy to see that
![]() $\delta (X)=\#(\mathbb N\setminus D_X)$
. If B is a finite codimension sub-
$\delta (X)=\#(\mathbb N\setminus D_X)$
. If B is a finite codimension sub-
![]() ${\mathbf {k}}$
-algebra of
${\mathbf {k}}$
-algebra of
![]() $\Gamma $
then
$\Gamma $
then
![]() $X=\operatorname {Spec}(B)$
is branch. We write
$X=\operatorname {Spec}(B)$
is branch. We write
![]() $D_B=D_X$
.
$D_B=D_X$
.
Let
![]() $\omega _{X}$
be the dualizing module of X; we can consider the composition of
$\omega _{X}$
be the dualizing module of X; we can consider the composition of
![]() ${\mathcal O}_{X}$
-module morphisms
${\mathcal O}_{X}$
-module morphisms
Let
![]() $d: {\mathcal O}_{X} \longrightarrow \Omega _{X}$
the universal derivation, then we have a
$d: {\mathcal O}_{X} \longrightarrow \Omega _{X}$
the universal derivation, then we have a
![]() ${\mathbf {k}}$
-linear map
${\mathbf {k}}$
-linear map
![]() $\gamma _X d$
that we also denote by
$\gamma _X d$
that we also denote by
![]() $d: {\mathcal O}_{X} \longrightarrow \omega _{X}.$
Recall that the Milnor number of X is
$d: {\mathcal O}_{X} \longrightarrow \omega _{X}.$
Recall that the Milnor number of X is
![]() $\mu (X)=\operatorname {dim}_{{\mathbf {k}}}(\omega _{X}/d {\mathcal O}_{X})$
, [Reference Buchweitz and Greuel5]. Since we only consider branches we have that
$\mu (X)=\operatorname {dim}_{{\mathbf {k}}}(\omega _{X}/d {\mathcal O}_{X})$
, [Reference Buchweitz and Greuel5]. Since we only consider branches we have that
![]() $\mu (X)=2\delta (X)$
(see [Reference Buchweitz and Greuel5, Proposition 1.2.1]). Notice that X is non-singular iff
$\mu (X)=2\delta (X)$
(see [Reference Buchweitz and Greuel5, Proposition 1.2.1]). Notice that X is non-singular iff
![]() $\mu (X)=0$
iff
$\mu (X)=0$
iff
![]() $\delta (X)=0$
iff
$\delta (X)=0$
iff
![]() $c(X)=0$
.
$c(X)=0$
.
We denote by
![]() $\pi :Bl(X)\longrightarrow X$
the blowing-up of X on its closed point. The fiber of the closed point of X has a finite number of closed points: the so-called points of the first neighborhood of X. We can iterate the process of blowing-up until we get the normalization of X (see [Reference Cutkosky7, Reference Northcott24]). We denote by
$\pi :Bl(X)\longrightarrow X$
the blowing-up of X on its closed point. The fiber of the closed point of X has a finite number of closed points: the so-called points of the first neighborhood of X. We can iterate the process of blowing-up until we get the normalization of X (see [Reference Cutkosky7, Reference Northcott24]). We denote by
![]() $\operatorname {Inf}(X)$
the set of infinitely near points of X. The curve singularity defined by an infinitely point p of X will be denote by
$\operatorname {Inf}(X)$
the set of infinitely near points of X. The curve singularity defined by an infinitely point p of X will be denote by
![]() $(X,p)$
; we set
$(X,p)$
; we set
![]() $(X,0)=X$
.
$(X,0)=X$
.
Proposition 2.1 Let X be a branch. Then
![]() $\mathrm{(i)}$
$\mathrm{(i)}$
![]() $\mathrm{(ii)}$
It holds
$\mathrm{(ii)}$
It holds
and
![]() $e_1(X)\le \binom {e_0(X)}{2} - \binom {n-1}{2}$
.
$e_1(X)\le \binom {e_0(X)}{2} - \binom {n-1}{2}$
.
![]() $\mathrm{(iii)}$
If X is singular, then
$\mathrm{(iii)}$
If X is singular, then
![]() $\delta (X)+1 \le c(X)\le 2 \delta (X)$
, and
$\delta (X)+1 \le c(X)\le 2 \delta (X)$
, and
![]() $c(X) = 2 \delta (X)$
if and only if
$c(X) = 2 \delta (X)$
if and only if
![]() ${\mathcal O}_{X}$
is a Gorenstein ring.
${\mathcal O}_{X}$
is a Gorenstein ring.
Proof
![]() $\mathrm{(i)}$
[Reference Northcott25].
$\mathrm{(i)}$
[Reference Northcott25].
![]() $\mathrm{(ii)}$
[Reference Buchweitz and Greuel5, Proposition 1.2.4(i)] and [Reference Elias10, Reference Elias12, Reference Northcott25].
$\mathrm{(ii)}$
[Reference Buchweitz and Greuel5, Proposition 1.2.4(i)] and [Reference Elias10, Reference Elias12, Reference Northcott25].
![]() $\mathrm{(iii)}$
[Reference Serre26, Proposition 7, page 80] and [Reference Bertin and Carbonne2].
$\mathrm{(iii)}$
[Reference Serre26, Proposition 7, page 80] and [Reference Bertin and Carbonne2].
3 Macaulay-like duality
In this section, we establish a Macaulay-like duality for the family of sub-
![]() ${\mathbf {k}}$
-algebras B of
${\mathbf {k}}$
-algebras B of
![]() $\Gamma ={\mathbf {k}}[\![t]\!]$
of finite codimension. For the classical Macaulay’s duality, see [Reference Iarrobino and Kanev20], [Reference Elias, Cuong, Hoa and Trung14], and for the generalization to higher dimension of Macaulay’s duality, see [Reference Elias and Rossi15]. Recall that Macaulay’s duality is a particular case of Matlis’ duality (see [Reference Bruns and Herzog4]).
$\Gamma ={\mathbf {k}}[\![t]\!]$
of finite codimension. For the classical Macaulay’s duality, see [Reference Iarrobino and Kanev20], [Reference Elias, Cuong, Hoa and Trung14], and for the generalization to higher dimension of Macaulay’s duality, see [Reference Elias and Rossi15]. Recall that Macaulay’s duality is a particular case of Matlis’ duality (see [Reference Bruns and Herzog4]).
We write
![]() $\Delta = {\mathbf {k}}[u]$
;
$\Delta = {\mathbf {k}}[u]$
;
![]() $\Gamma $
is a
$\Gamma $
is a
![]() $\Delta $
-module with
$\Delta $
-module with
![]() $\Delta $
acting on
$\Delta $
acting on
![]() $\Gamma $
by derivation. This action denoted by
$\Gamma $
by derivation. This action denoted by
![]() $\circ $
is defined by
$\circ $
is defined by
where
![]() $ \partial _{t} $
denotes the derivative with respect to t. This action induces a non-singular
$ \partial _{t} $
denotes the derivative with respect to t. This action induces a non-singular
![]() ${\mathbf {k}}$
-bilinear perfect pairing:
${\mathbf {k}}$
-bilinear perfect pairing:
Definition 3.1 Given a sub-
![]() ${\mathbf {k}}$
-algebra B of
${\mathbf {k}}$
-algebra B of
![]() $\Gamma ={\mathbf {k}}[\![t]\!]$
we define
$\Gamma ={\mathbf {k}}[\![t]\!]$
we define
![]() $B^{\perp }$
as the set of
$B^{\perp }$
as the set of
![]() $g\in \Delta $
such that
$g\in \Delta $
such that
![]() $g\perp f=0$
for all
$g\perp f=0$
for all
![]() $f\in B$
. Notice that
$f\in B$
. Notice that
![]() $B^{\perp }$
is a
$B^{\perp }$
is a
![]() ${\mathbf {k}}$
-vector subspace of
${\mathbf {k}}$
-vector subspace of
![]() $\Delta $
, this is, following the classic Macaulay’s duality terminology, the inverse system of B. Given a
$\Delta $
, this is, following the classic Macaulay’s duality terminology, the inverse system of B. Given a
![]() ${\mathbf {k}}$
-vector subspace
${\mathbf {k}}$
-vector subspace
![]() $V\subset \Delta $
we consider
$V\subset \Delta $
we consider
![]() $\operatorname {Ann}(V)\subset \Gamma $
as the set of power series
$\operatorname {Ann}(V)\subset \Gamma $
as the set of power series
![]() $f\in \Gamma $
such that
$f\in \Gamma $
such that
![]() $g\perp f=0$
for all
$g\perp f=0$
for all
![]() $g\in V$
.
$g\in V$
.
Let B be a finite codimension sub-
![]() ${\mathbf {k}}$
-algebra of
${\mathbf {k}}$
-algebra of
![]() $\Gamma $
. Then we have a non-singular
$\Gamma $
. Then we have a non-singular
![]() ${\mathbf {k}}$
-bilinear perfect pairing:
${\mathbf {k}}$
-bilinear perfect pairing:
 $$ \begin{align} \begin{array}{ cclc} \perp: &B^{\perp} \times \frac{\Gamma}{B}&\longrightarrow & {\mathbf{k}} \\ & (g,\overline{f})&\mapsto & g\perp f. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{ cclc} \perp: &B^{\perp} \times \frac{\Gamma}{B}&\longrightarrow & {\mathbf{k}} \\ & (g,\overline{f})&\mapsto & g\perp f. \end{array} \end{align} $$
We denote by
![]() $Perp(B)$
, the
$Perp(B)$
, the
![]() ${\mathbf {k}}$
-vector space of maps
${\mathbf {k}}$
-vector space of maps
for all
![]() $g\in \Delta $
. These maps are the elements of the dual space of B with finite support:
$g\in \Delta $
. These maps are the elements of the dual space of B with finite support:
![]() $g^{\perp }(\max _B^d)=0$
for
$g^{\perp }(\max _B^d)=0$
for
![]() $d>\operatorname {deg}(g)$
. We denote by
$d>\operatorname {deg}(g)$
. We denote by
![]() $Der_{{\mathbf {k}}}(B)$
the
$Der_{{\mathbf {k}}}(B)$
the
![]() ${\mathbf {k}}$
-vector space of
${\mathbf {k}}$
-vector space of
![]() ${\mathbf {k}}$
-derivations of B. Since
${\mathbf {k}}$
-derivations of B. Since
![]() $Der_{{\mathbf {k}}}(B)\cong (\max _B/\max _B^2)^*$
, we can identify
$Der_{{\mathbf {k}}}(B)\cong (\max _B/\max _B^2)^*$
, we can identify
![]() $Der_{{\mathbf {k}}}(B)$
with the
$Der_{{\mathbf {k}}}(B)$
with the
![]() ${\mathbf {k}}$
-vector space of elements
${\mathbf {k}}$
-vector space of elements
![]() $\sigma $
of the dual space of B such that
$\sigma $
of the dual space of B such that
![]() $\sigma (\max _B^2)=0$
.
$\sigma (\max _B^2)=0$
.
We have
![]() $Der_{{\mathbf {k}}}(B)\subset Perp(B)$
, this inclusion is strict. Let us consider the codimension
$Der_{{\mathbf {k}}}(B)\subset Perp(B)$
, this inclusion is strict. Let us consider the codimension
![]() $8$
algebra
$8$
algebra
![]() $B={\mathbf {k}}[\![t^4,t^7,t^{17}]\!]$
. The linear map
$B={\mathbf {k}}[\![t^4,t^7,t^{17}]\!]$
. The linear map
![]() $(u^{11})^{\perp }:B\longrightarrow {\mathbf {k}}$
is not a derivation since
$(u^{11})^{\perp }:B\longrightarrow {\mathbf {k}}$
is not a derivation since
![]() $t^{11}\in \max _B^2$
and
$t^{11}\in \max _B^2$
and
![]() $(u^{11}){\perp }(t^{11})=11!\neq 0$
.
$(u^{11}){\perp }(t^{11})=11!\neq 0$
.
Next step is to characterize the vector
![]() ${\mathbf {k}}$
-vector subspaces
${\mathbf {k}}$
-vector subspaces
![]() $B^{\perp }$
of
$B^{\perp }$
of
![]() $\Delta ,$
where B ranges the family of finite codimension sub-
$\Delta ,$
where B ranges the family of finite codimension sub-
![]() ${\mathbf {k}}$
-algebras of
${\mathbf {k}}$
-algebras of
![]() $\Gamma $
. First, we give some properties of
$\Gamma $
. First, we give some properties of
![]() $B^{\perp }$
that we will use along the paper.
$B^{\perp }$
that we will use along the paper.
Given a polynomial
![]() $g=\sum _{i=0}^d a_i u^i\in \Delta $
we denote by
$g=\sum _{i=0}^d a_i u^i\in \Delta $
we denote by
![]() $\mathrm {{Supp}}(g)$
the support of g: the finite set of integers i such that
$\mathrm {{Supp}}(g)$
the support of g: the finite set of integers i such that
![]() $a_i\neq 0$
.
$a_i\neq 0$
.
Proposition 3.2 Let
![]() $B\subset \Gamma $
be a codimension
$B\subset \Gamma $
be a codimension
![]() $\delta $
sub-
$\delta $
sub-
![]() ${\mathbf {k}}$
-algebra B of
${\mathbf {k}}$
-algebra B of
![]() $\Gamma ,$
and let
$\Gamma ,$
and let
![]() $\mathcal C=(t^c)$
be the conductor of the extension
$\mathcal C=(t^c)$
be the conductor of the extension
![]() $B\subset \Gamma $
. Then:
$B\subset \Gamma $
. Then:
-
(1)
 $\operatorname {dim}_{{\mathbf {k}}}(B^{\perp })=\delta $
.
$\operatorname {dim}_{{\mathbf {k}}}(B^{\perp })=\delta $
. -
(2) For all
 $g\in B^{\perp }$
, we have
$g\in B^{\perp }$
, we have
 $ \mathrm {{Supp}}(g)\subset [1, c-1]$
, and
$ \mathrm {{Supp}}(g)\subset [1, c-1]$
, and  $$ \begin{align*}u^{[1, e_0(B)-1]}=\{u^i; i\in [1, e_0(B)-1]\} \subset B^{\perp}\subset \langle u, u^2, \dots , u^{c-1}\rangle. \end{align*} $$
$$ \begin{align*}u^{[1, e_0(B)-1]}=\{u^i; i\in [1, e_0(B)-1]\} \subset B^{\perp}\subset \langle u, u^2, \dots , u^{c-1}\rangle. \end{align*} $$
-
(3) The following conditions are equivalent:
-
(i)
 $\delta =0$
,
$\delta =0$
, -
(ii)
 $B=\Gamma $
,
$B=\Gamma $
, -
(iii)
 $B^{\perp }=0$
,
$B^{\perp }=0$
, -
(iv)
 $B^{\perp }\subset \langle u^2,u^3,\dots \rangle $
.
$B^{\perp }\subset \langle u^2,u^3,\dots \rangle $
.
-
Proof
![]() $(1)$
Since
$(1)$
Since
![]() $\perp $
is a
$\perp $
is a
![]() ${\mathbf {k}}$
-bilinear perfect pairing, we get
${\mathbf {k}}$
-bilinear perfect pairing, we get
![]() $\operatorname {dim}_{{\mathbf {k}}}(B^{\perp })=\delta $
, see the equation (2).
$\operatorname {dim}_{{\mathbf {k}}}(B^{\perp })=\delta $
, see the equation (2).
![]() $(2)$
Since B is a
$(2)$
Since B is a
![]() ${\mathbf {k}}$
-algebra, we have
${\mathbf {k}}$
-algebra, we have
![]() $1\in B$
, so if
$1\in B$
, so if
![]() $g=\sum _{j\ge 0} a_iu^i\in B^{\perp }$
, then
$g=\sum _{j\ge 0} a_iu^i\in B^{\perp }$
, then
![]() $0=g\perp 1= a_0$
. Hence
$0=g\perp 1= a_0$
. Hence
![]() $B^{\perp }\subset \langle u, u^2, \dots \rangle $
. We know that
$B^{\perp }\subset \langle u, u^2, \dots \rangle $
. We know that
![]() $(t^c)\subset B$
so for all
$(t^c)\subset B$
so for all
![]() $g=\sum _{j\ge 0} a_iu^i\in B^{\perp }$
, we have
$g=\sum _{j\ge 0} a_iu^i\in B^{\perp }$
, we have
![]() $i\ge 0$
. Hence, if
$i\ge 0$
. Hence, if
![]() $g\in B^{\perp }$
, then
$g\in B^{\perp }$
, then
![]() $\operatorname {deg}(g)\le c-1$
. From this, we deduce that
$\operatorname {deg}(g)\le c-1$
. From this, we deduce that
![]() $B^{\perp }\subset \langle u, u^2, \dots , u^{c-1}\rangle $
.
$B^{\perp }\subset \langle u, u^2, \dots , u^{c-1}\rangle $
.
Notice that
![]() $v_t(f)\ge e_0(B)$
for all
$v_t(f)\ge e_0(B)$
for all
![]() $f\in B\setminus \{1\}$
, so given
$f\in B\setminus \{1\}$
, so given
![]() $i\in [1, e_0(B)-1]$
we have
$i\in [1, e_0(B)-1]$
we have
![]() $u^i\perp f=0$
. Hence
$u^i\perp f=0$
. Hence
![]() $u^i\in B^{\perp }$
and then
$u^i\in B^{\perp }$
and then
![]() $u^{[1, e_0(B)-1]}\subset B^{\perp }$
.
$u^{[1, e_0(B)-1]}\subset B^{\perp }$
.
![]() $(3)$
The condition of
$(3)$
The condition of
![]() $(i)$
is equivalent to
$(i)$
is equivalent to
![]() $(ii)$
.
$(ii)$
.
![]() $(ii)$
trivially implies
$(ii)$
trivially implies
![]() $(iii)$
and this implies
$(iii)$
and this implies
![]() $(iv)$
. If
$(iv)$
. If
![]() $B^{\perp }\subset \langle u^2,u^3,\dots \rangle $
, then
$B^{\perp }\subset \langle u^2,u^3,\dots \rangle $
, then
![]() $t\in B$
, since B is a
$t\in B$
, since B is a
![]() ${\mathbf {k}}$
-algebra, we get
${\mathbf {k}}$
-algebra, we get
![]() $(ii)$
.
$(ii)$
.
For all power series
![]() $f=\sum _{i\ge 0} b_i t^i\in \Gamma $
and given a nonnegative integer
$f=\sum _{i\ge 0} b_i t^i\in \Gamma $
and given a nonnegative integer
![]() $s\in \mathbb N$
, we denote by
$s\in \mathbb N$
, we denote by
![]() $[f]_{\le s}$
the truncated polynomial
$[f]_{\le s}$
the truncated polynomial
![]() $[f]_{\le s}=\sum _{i\ge 0}^s b_i t^i$
.
$[f]_{\le s}=\sum _{i\ge 0}^s b_i t^i$
.
Let B be a finite codimension sub-
![]() ${\mathbf {k}}$
-algebra of
${\mathbf {k}}$
-algebra of
![]() $\Gamma $
with conductor c. Then B is a finitely generated
$\Gamma $
with conductor c. Then B is a finitely generated
![]() ${\mathbf {k}}$
-algebra; let
${\mathbf {k}}$
-algebra; let
![]() $f_1,\dots ,f_r$
be a system of generators of B as
$f_1,\dots ,f_r$
be a system of generators of B as
![]() ${\mathbf {k}}$
-algebra. We denote by
${\mathbf {k}}$
-algebra. We denote by
![]() $\natural _{B,d}$
,
$\natural _{B,d}$
,
![]() $d\ge c-1$
, the finite set of polynomials
$d\ge c-1$
, the finite set of polynomials
![]() $[f_1^{l_1}\dots f_r^{l_r}]_{\le d}$
with
$[f_1^{l_1}\dots f_r^{l_r}]_{\le d}$
with
![]() $l_i\ge 0$
,
$l_i\ge 0$
,
![]() $i=1,\dots ,r$
, and
$i=1,\dots ,r$
, and
![]() $l_1+\cdots +l_r\le d$
. We denote by
$l_1+\cdots +l_r\le d$
. We denote by
![]() $W(\{f_1,\dots , f_r\},d)\subset \Delta $
the
$W(\{f_1,\dots , f_r\},d)\subset \Delta $
the
![]() ${\mathbf {k}}$
-vector space generated by the polynomials of
${\mathbf {k}}$
-vector space generated by the polynomials of
![]() $\natural _{B,d}$
. Notice that
$\natural _{B,d}$
. Notice that
![]() $W(\{f_1,\dots , f_r\},d)+\langle t^{d+1}\rangle =W(\{f_1,\dots , f_r\},d+1)$
.
$W(\{f_1,\dots , f_r\},d)+\langle t^{d+1}\rangle =W(\{f_1,\dots , f_r\},d+1)$
.
Proposition 3.3 Let B be a finite codimension sub-
![]() ${\mathbf {k}}$
-algebra of
${\mathbf {k}}$
-algebra of
![]() $\Gamma $
with conductor c. Then
$\Gamma $
with conductor c. Then
![]() $B^{\perp }$
is the set of
$B^{\perp }$
is the set of
![]() $g\in \Delta $
of degree at most
$g\in \Delta $
of degree at most
![]() $c-1$
and such that
$c-1$
and such that
![]() $g\perp h=0$
for all
$g\perp h=0$
for all
![]() ${h\in \natural _{B,c-1}}$
.
${h\in \natural _{B,c-1}}$
.
Proof Let
![]() $f_1,\dots ,f_r$
be a system of generators of B as
$f_1,\dots ,f_r$
be a system of generators of B as
![]() ${\mathbf {k}}$
-algebra, and let
${\mathbf {k}}$
-algebra, and let
![]() $\natural _{B,c-1}$
be the associated set of polynomials.
$\natural _{B,c-1}$
be the associated set of polynomials.
If
![]() $g\in B^{\perp }$
, then
$g\in B^{\perp }$
, then
![]() $\operatorname {deg}(g)\le c-1$
, Proposition 3.2(2), so
$\operatorname {deg}(g)\le c-1$
, Proposition 3.2(2), so
Hence,
![]() $g\perp h=0$
for all
$g\perp h=0$
for all
![]() $h\in \natural _{B,c-1}$
.
$h\in \natural _{B,c-1}$
.
Let
![]() $g \in \Delta $
be a polynomial with
$g \in \Delta $
be a polynomial with
![]() $\operatorname {deg}(g)\le c-1$
and such that
$\operatorname {deg}(g)\le c-1$
and such that
![]() $g\perp h=0$
for all
$g\perp h=0$
for all
![]() $h\in \natural _{B,c-1}$
. Any
$h\in \natural _{B,c-1}$
. Any
![]() $f\in B$
can be written as
$f\in B$
can be written as
with
![]() $c_{l_1,\dots ,l_r}\in {\mathbf {k}}$
. Since
$c_{l_1,\dots ,l_r}\in {\mathbf {k}}$
. Since
![]() $\operatorname {deg}(g)\le c-1,$
we have
$\operatorname {deg}(g)\le c-1,$
we have
so
![]() $g\in B^{\perp }$
.
$g\in B^{\perp }$
.
Remark 3.4 Notice that Proposition 3.3 shows that the computation of
![]() $B^{\perp }$
is effective. In fact, in the set
$B^{\perp }$
is effective. In fact, in the set
![]() $\natural _{B,c-1}$
, there are involved a finite number of monomials and we only have to consider polynomials g of degree at most
$\natural _{B,c-1}$
, there are involved a finite number of monomials and we only have to consider polynomials g of degree at most
![]() $c-1$
.
$c-1$
.
Remark 3.5 Although
![]() $B^{\perp }$
is a
$B^{\perp }$
is a
![]() ${\mathbf {k}}$
-vector subspace of
${\mathbf {k}}$
-vector subspace of
![]() $\Delta $
for any sub-
$\Delta $
for any sub-
![]() ${\mathbf {k}}$
-algebra B of
${\mathbf {k}}$
-algebra B of
![]() $\Gamma $
, not all
$\Gamma $
, not all
![]() $\operatorname {Ann}(V)$
is a
$\operatorname {Ann}(V)$
is a
![]() ${\mathbf {k}}$
-algebra for a given
${\mathbf {k}}$
-algebra for a given
![]() ${\mathbf {k}}$
-vector subspace
${\mathbf {k}}$
-vector subspace
![]() $V\subset \Delta $
. In fact, let us consider the
$V\subset \Delta $
. In fact, let us consider the
![]() ${\mathbf {k}}$
-vector subspace
${\mathbf {k}}$
-vector subspace
![]() $V\subset \Delta $
generated by
$V\subset \Delta $
generated by
![]() $u^2$
. Then
$u^2$
. Then
![]() $\operatorname {Ann}(V)$
is the set of
$\operatorname {Ann}(V)$
is the set of
![]() $f=\sum _{i\ge 0}a_it^i\in \Gamma $
such that
$f=\sum _{i\ge 0}a_it^i\in \Gamma $
such that
![]() $a_2=0$
. This is not a
$a_2=0$
. This is not a
![]() ${\mathbf {k}}$
-algebra because
${\mathbf {k}}$
-algebra because
![]() $u^2\perp t=0$
, so
$u^2\perp t=0$
, so
![]() $t\in \operatorname {Ann}(V)$
and
$t\in \operatorname {Ann}(V)$
and
![]() $u^2\perp t^2=2\neq 0$
, so
$u^2\perp t^2=2\neq 0$
, so
![]() $t^2\notin \operatorname {Ann}(V)$
.
$t^2\notin \operatorname {Ann}(V)$
.
Definition 3.6 A finite dimensional
![]() ${\mathbf {k}}$
-vector subspace
${\mathbf {k}}$
-vector subspace
![]() $V\subset \Delta $
is so-called algebra-forming with respect to a
$V\subset \Delta $
is so-called algebra-forming with respect to a
![]() ${\mathbf {k}}$
-algebra
${\mathbf {k}}$
-algebra
![]() $B\subset \Gamma $
iff the following conditions hold:
$B\subset \Gamma $
iff the following conditions hold:
-
(a)
 $g(0)=0$
for all
$g(0)=0$
for all
 $g\in V$
and,
$g\in V$
and, -
(b) for all
 $f\in B$
such that
$f\in B$
such that
 $g\perp f=0$
for all
$g\perp f=0$
for all
 $g\in V$
it holds
$g\in V$
it holds
 $g\perp f^2=0$
for all
$g\perp f^2=0$
for all
 $g\in V$
.
$g\in V$
.
An element
![]() $g\in \Delta $
is so-called algebra-forming with respect to B if
$g\in \Delta $
is so-called algebra-forming with respect to B if
![]() $V=\langle g\rangle $
is algebra-forming with respect to B.
$V=\langle g\rangle $
is algebra-forming with respect to B.
Example 3.7 Let us consider the codimension
![]() $\delta =4$
algebra
$\delta =4$
algebra
![]() $B={\mathbf {k}}[\![t^3+t^4,t^5]\!]$
of
$B={\mathbf {k}}[\![t^3+t^4,t^5]\!]$
of
![]() $\Gamma $
. The conductor of B is
$\Gamma $
. The conductor of B is
![]() $c=8$
. Then
$c=8$
. Then
![]() $B^{\perp }$
is the set of polynomials
$B^{\perp }$
is the set of polynomials
![]() $g\in \Delta $
of degree at most
$g\in \Delta $
of degree at most
![]() $7$
such that
$7$
such that
![]() $g\perp f=0$
for
$g\perp f=0$
for
![]() $f\in \natural _{B,c-1}=\{t^3+t^4, t^5, t^6+2t^7\}$
. A simple computation shows that
$f\in \natural _{B,c-1}=\{t^3+t^4, t^5, t^6+2t^7\}$
. A simple computation shows that
![]() $B^{\perp }$
is the
$B^{\perp }$
is the
![]() ${\mathbf {k}}$
-vector space generated by the four linear independent polynomials
${\mathbf {k}}$
-vector space generated by the four linear independent polynomials
![]() $u, u^2, u^3-\frac {1}{4}u^4, u^6-\frac {1}{2.7}u^7$
. Let us consider
$u, u^2, u^3-\frac {1}{4}u^4, u^6-\frac {1}{2.7}u^7$
. Let us consider
then we have
![]() $B_2=\operatorname {Ann}\langle u^2\rangle \cap B_3$
, i.e.,
$B_2=\operatorname {Ann}\langle u^2\rangle \cap B_3$
, i.e.,
![]() $u^2$
is an algebra-forming element with respect to
$u^2$
is an algebra-forming element with respect to
![]() $B_2$
.
$B_2$
.
In the following result, we prove that, in fact, if
![]() $V\subset \Delta $
is algebra-forming with respect to a
$V\subset \Delta $
is algebra-forming with respect to a
![]() ${\mathbf {k}}$
algebra
${\mathbf {k}}$
algebra
![]() $B\subset \Gamma ,$
then
$B\subset \Gamma ,$
then
![]() $\operatorname {Ann}(V)\cap B$
is a sub-
$\operatorname {Ann}(V)\cap B$
is a sub-
![]() ${\mathbf {k}}$
-algebra of
${\mathbf {k}}$
-algebra of
![]() $\Gamma $
.
$\Gamma $
.
Proposition 3.8 Let
![]() $V\subset \Delta $
be an algebra-forming
$V\subset \Delta $
be an algebra-forming
![]() ${\mathbf {k}}$
-vector subspace with respect to a
${\mathbf {k}}$
-vector subspace with respect to a
![]() ${\mathbf {k}}$
-algebra
${\mathbf {k}}$
-algebra
![]() $B\subset \Gamma $
. Then
$B\subset \Gamma $
. Then
![]() $\operatorname {Ann}(V)\cap B$
is a sub-
$\operatorname {Ann}(V)\cap B$
is a sub-
![]() ${\mathbf {k}}$
-algebra of
${\mathbf {k}}$
-algebra of
![]() $\Gamma $
.
$\Gamma $
.
Proof Clearly
![]() $C=\operatorname {Ann}(V)\cap B$
is a
$C=\operatorname {Ann}(V)\cap B$
is a
![]() ${\mathbf {k}}$
-vector subspace of
${\mathbf {k}}$
-vector subspace of
![]() $\Gamma $
. Given
$\Gamma $
. Given
![]() $f_1, f_2\in C$
we have that
$f_1, f_2\in C$
we have that
![]() $f_1+f_2\in C$
and from
$f_1+f_2\in C$
and from
we deduce that
![]() $g\perp (f_1 f_2)=0$
, i.e.,
$g\perp (f_1 f_2)=0$
, i.e.,
![]() $f_1f_2\in C$
. Since
$f_1f_2\in C$
. Since
![]() $g(0)=0$
for all
$g(0)=0$
for all
![]() $g\in V$
we get
$g\in V$
we get
![]() $1\in C$
, so C is a sub-
$1\in C$
, so C is a sub-
![]() ${\mathbf {k}}$
-algebra of
${\mathbf {k}}$
-algebra of
![]() $\Gamma $
.
$\Gamma $
.
The following result is an extension of Macaulay’s duality to finite codimension sub-
![]() ${\mathbf {k}}$
-algebras
${\mathbf {k}}$
-algebras
![]() $B\subset \Gamma $
.
$B\subset \Gamma $
.
Theorem 3.9 Given a nonnegative integers
![]() $\delta> 0$
and
$\delta> 0$
and
![]() $c\ge \delta + 1$
, there is a one-to-one correspondence
$c\ge \delta + 1$
, there is a one-to-one correspondence
![]() $\perp $
between the following sets:
$\perp $
between the following sets:
-
(1) sub-
 ${\mathbf {k}}$
-algebras B of
${\mathbf {k}}$
-algebras B of
 $\Gamma $
of codimension
$\Gamma $
of codimension
 $\delta $
as
$\delta $
as
 ${\mathbf {k}}$
-vector spaces such that the conductor of
${\mathbf {k}}$
-vector spaces such that the conductor of
 $B\subset \Gamma $
is
$B\subset \Gamma $
is
 $(t^c)$
,
$(t^c)$
, -
(2) algebra forming, with respect to
 $\Gamma $
,
$\Gamma $
,
 ${\mathbf {k}}$
-vector subspace
${\mathbf {k}}$
-vector subspace
 $V\subset \Delta $
of dimension
$V\subset \Delta $
of dimension
 $\delta $
, generated by polynomials of degree at most
$\delta $
, generated by polynomials of degree at most
 $c-1$
and such that there is a polynomial
$c-1$
and such that there is a polynomial
 $g\in V$
with
$g\in V$
with
 $\operatorname {deg}(g)=c-1$
.
$\operatorname {deg}(g)=c-1$
.
This correspondence is inclusion reversing: given two sub-
![]() ${\mathbf {k}}$
-algebras
${\mathbf {k}}$
-algebras
![]() $B_1$
and
$B_1$
and
![]() $B_2$
of
$B_2$
of
![]() $\Gamma $
,
$\Gamma $
,
![]() $B_1\subset B_2$
if and only if
$B_1\subset B_2$
if and only if
![]() $B_2^{\perp }\subset B_1^{\perp }$
.
$B_2^{\perp }\subset B_1^{\perp }$
.
Proof Let B be a sub-
![]() ${\mathbf {k}}$
-algebra B of
${\mathbf {k}}$
-algebra B of
![]() $\Gamma $
. Since we have a non-singular
$\Gamma $
. Since we have a non-singular
![]() ${\mathbf {k}}$
-bilinear pairing:
${\mathbf {k}}$
-bilinear pairing:
 $$ \begin{align*}\begin{array}{ cclc} \perp: &B^{\perp} \times \frac{\Gamma}{B}&\longrightarrow & {\mathbf{k}} \\ & (g,\overline{f})&\mapsto & g\perp f, \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ cclc} \perp: &B^{\perp} \times \frac{\Gamma}{B}&\longrightarrow & {\mathbf{k}} \\ & (g,\overline{f})&\mapsto & g\perp f, \end{array} \end{align*} $$
we get that
![]() $B^{\perp }$
is a
$B^{\perp }$
is a
![]() ${\mathbf {k}}$
-vector subspace of dimension
${\mathbf {k}}$
-vector subspace of dimension
![]() $\delta $
of
$\delta $
of
![]() $\Delta $
. By definition
$\Delta $
. By definition
![]() $B^{\perp }$
is algebra-forming with respect to
$B^{\perp }$
is algebra-forming with respect to
![]() $\Gamma $
. Being c the conductor we have
$\Gamma $
. Being c the conductor we have
![]() $(t^c)\subset B$
, so
$(t^c)\subset B$
, so
![]() $\operatorname {deg}(g)\le c-1$
for all
$\operatorname {deg}(g)\le c-1$
for all
![]() $g\in B^{\perp }$
and there exist
$g\in B^{\perp }$
and there exist
![]() $g\in B^{\perp }$
of degree
$g\in B^{\perp }$
of degree
![]() $c-1$
.
$c-1$
.
Let V be an algebra forming, with respect to
![]() $\Gamma $
,
$\Gamma $
,
![]() ${\mathbf {k}}$
-vector subspace satisfying the conditions of (2). Let us consider the
${\mathbf {k}}$
-vector subspace satisfying the conditions of (2). Let us consider the
![]() ${\mathbf {k}}$
-algebra
${\mathbf {k}}$
-algebra
![]() $B=\operatorname {Ann}(V)$
. From the perfect pairing (1), we get that the codimension of B in
$B=\operatorname {Ann}(V)$
. From the perfect pairing (1), we get that the codimension of B in
![]() $\Gamma $
is
$\Gamma $
is
![]() $\delta $
. Since V is generated by polynomials of degree at most
$\delta $
. Since V is generated by polynomials of degree at most
![]() $c-1$
we have that
$c-1$
we have that
![]() $(t^c)\subset B$
, so the conductor of B is at most c. Furthermore, since there is
$(t^c)\subset B$
, so the conductor of B is at most c. Furthermore, since there is
![]() $g\in V$
with
$g\in V$
with
![]() $\operatorname {deg}(g)=c-1$
we deduce that c is the conductor of B.
$\operatorname {deg}(g)=c-1$
we deduce that c is the conductor of B.
It is straightforward to prove the inclusion reversing from the definition of the inverse system
![]() $B^{\perp }$
.
$B^{\perp }$
.
We end this section by describing the
![]() ${\mathbf {k}}$
-linear maps
${\mathbf {k}}$
-linear maps
![]() $B_2^{\perp }\longrightarrow B_1^{\perp }$
induced by
$B_2^{\perp }\longrightarrow B_1^{\perp }$
induced by
![]() ${\mathbf {k}}$
-algebra isomorphisms
${\mathbf {k}}$
-algebra isomorphisms
![]() $B_1\longrightarrow B_2$
between two finite codimension
$B_1\longrightarrow B_2$
between two finite codimension
![]() ${\mathbf {k}}$
-algebras
${\mathbf {k}}$
-algebras
![]() $B_1$
and
$B_1$
and
![]() $B_2$
of
$B_2$
of
![]() $\Gamma $
. Let c be an integer bigger than the conductors of
$\Gamma $
. Let c be an integer bigger than the conductors of
![]() $B_1$
and
$B_1$
and
![]() $B_2$
.
$B_2$
.
The perfect pairing (1) induce a perfect pairing
 $$ \begin{align*}\begin{array}{ lclc} \perp: & \Delta_{\le c-1} \times \frac{\Gamma}{(t^c)} &\longrightarrow & {\mathbf{k}} \\ & (g,\overline{f})&\mapsto & g\perp f=(g\circ f)(0), \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ lclc} \perp: & \Delta_{\le c-1} \times \frac{\Gamma}{(t^c)} &\longrightarrow & {\mathbf{k}} \\ & (g,\overline{f})&\mapsto & g\perp f=(g\circ f)(0), \end{array} \end{align*} $$
where
![]() $\Delta _{\le c-1}$
is the
$\Delta _{\le c-1}$
is the
![]() ${\mathbf {k}}$
-vector space of polynomials of degree at most
${\mathbf {k}}$
-vector space of polynomials of degree at most
![]() $c-1$
. We consider the usual
$c-1$
. We consider the usual
![]() ${\mathbf {k}}$
-vector basis of
${\mathbf {k}}$
-vector basis of
![]() $\Gamma /(t^c)$
of the cosets of
$\Gamma /(t^c)$
of the cosets of
![]() $t^i$
,
$t^i$
,
![]() $i=0,\dots , c-1$
. Its dual basis is
$i=0,\dots , c-1$
. Its dual basis is
![]() $\frac {1}{i!} u^i$
,
$\frac {1}{i!} u^i$
,
![]() $i=0,\dots , c-1$
, since
$i=0,\dots , c-1$
, since
![]() $1\le i, j \le c-1$
.
$1\le i, j \le c-1$
.
The
![]() ${\mathbf {k}}$
-algebra
${\mathbf {k}}$
-algebra
![]() $B_i$
has conductor at most c so we can consider that
$B_i$
has conductor at most c so we can consider that
![]() $B_i\subset \Gamma /(t^{c})$
,
$B_i\subset \Gamma /(t^{c})$
,
![]() $i=1,2$
. On the other hand, from Proposition 3.2, we have that
$i=1,2$
. On the other hand, from Proposition 3.2, we have that
![]() $B_i^{\perp }\subset \Delta _{\le c-1}$
,
$B_i^{\perp }\subset \Delta _{\le c-1}$
,
![]() $i=1,2$
.
$i=1,2$
.
If
![]() $B_1$
is isomorphic to
$B_1$
is isomorphic to
![]() $B_2$
by
$B_2$
by
![]() $\phi $
, then their normalizations are isomorphic:
$\phi $
, then their normalizations are isomorphic:
This automorphism is determined by a power series
![]() $h(t)\in (t)$
such that
$h(t)\in (t)$
such that
![]() $u\perp h\neq 0$
and
$u\perp h\neq 0$
and
 $$ \begin{align*}\begin{array}{ lclc} \overline{\phi}: & \Gamma &\longrightarrow & \Gamma \\ & f &\mapsto & f(h). \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ lclc} \overline{\phi}: & \Gamma &\longrightarrow & \Gamma \\ & f &\mapsto & f(h). \end{array} \end{align*} $$
Then we have an isomorphism of
![]() ${\mathbf {k}}$
-vector spaces
${\mathbf {k}}$
-vector spaces
and the perfect pairing induces a
![]() ${\mathbf {k}}$
-vector isomorphism
${\mathbf {k}}$
-vector isomorphism
The matrix
![]() $M_{\phi }$
associated with
$M_{\phi }$
associated with
![]() $\phi $
in the basis
$\phi $
in the basis
![]() ${t^i}$
,
${t^i}$
,
![]() $i=0,\dots , c-1$
, is the
$i=0,\dots , c-1$
, is the
![]() $c\times c$
matrix whose columns are the coefficients of
$c\times c$
matrix whose columns are the coefficients of
![]() $\phi ({t}^i)={h}^i$
,
$\phi ({t}^i)={h}^i$
,
![]() $i=0,\dots , c-1$
, with respect to this basis. Hence, the matrix of
$i=0,\dots , c-1$
, with respect to this basis. Hence, the matrix of
![]() $\phi ^*:B_2^*=B_2^{\perp }\longrightarrow B_1^*=B_1^{\perp }$
with respect to the basis
$\phi ^*:B_2^*=B_2^{\perp }\longrightarrow B_1^*=B_1^{\perp }$
with respect to the basis
![]() $\frac {1}{i!} u^i$
,
$\frac {1}{i!} u^i$
,
![]() $i=0,\dots , c-1$
, is the transpose matrix
$i=0,\dots , c-1$
, is the transpose matrix
![]() $^\tau M_{\phi }$
of
$^\tau M_{\phi }$
of
![]() $M_{\phi }$
.
$M_{\phi }$
.
Example 3.10 Let
![]() $B_2\subset \Gamma $
be a
$B_2\subset \Gamma $
be a
![]() ${\mathbf {k}}$
-algebra generated by two elements
${\mathbf {k}}$
-algebra generated by two elements
![]() $f_1$
,
$f_1$
,
![]() $f_2$
with
$f_2$
with
![]() $v_t(f_1)=2$
and
$v_t(f_1)=2$
and
![]() $v_t(f_2)=7$
. We may assume that
$v_t(f_2)=7$
. We may assume that
![]() $f_1=t^2+$
monomials of higher degree. Then
$f_1=t^2+$
monomials of higher degree. Then
![]() $B_2$
is of finite codimension
$B_2$
is of finite codimension
![]() $\delta =3$
and conductor
$\delta =3$
and conductor
![]() $c=6$
.
$c=6$
.
Since
![]() $\Gamma $
is complete there exist a power series
$\Gamma $
is complete there exist a power series
![]() $h\in (t)$
such that
$h\in (t)$
such that
![]() $h^2=f_1$
; we write
$h^2=f_1$
; we write
![]() $h=t+h_2 t^2+\dots +h_5 t^5+\dots $
. Notice that
$h=t+h_2 t^2+\dots +h_5 t^5+\dots $
. Notice that
![]() $\Gamma ={\mathbf {k}}[\![h]\!]$
.
$\Gamma ={\mathbf {k}}[\![h]\!]$
.
Let
![]() ${\phi }$
the automorphism of
${\phi }$
the automorphism of
![]() $\Gamma $
defined by h, i.e.,
$\Gamma $
defined by h, i.e.,
![]() ${\phi }(f)=f(h)$
. Then
${\phi }(f)=f(h)$
. Then
![]() $\phi ^{-1}(B_2)$
is a
$\phi ^{-1}(B_2)$
is a
![]() ${\mathbf {k}}$
-algebra
${\mathbf {k}}$
-algebra
![]() $B_1$
generated by
$B_1$
generated by
![]() $f_1'=t^2$
and
$f_1'=t^2$
and
![]() $f_2'(h)$
such that
$f_2'(h)$
such that
![]() $v_h(f_2' )=7$
. After a change of generators
$v_h(f_2' )=7$
. After a change of generators
![]() $B_1$
is generated by
$B_1$
is generated by
![]() $f_1'=t^2$
and
$f_1'=t^2$
and
![]() $f_2'=t^7$
.
$f_2'=t^7$
.
The induced isomorphism
![]() $\phi :B_1\longrightarrow B_2$
has the following
$\phi :B_1\longrightarrow B_2$
has the following
![]() $6 \times 6$
associated matrix with respect the basis
$6 \times 6$
associated matrix with respect the basis
![]() ${t^i}$
,
${t^i}$
,
![]() $i=0,\dots , 5$
,
$i=0,\dots , 5$
,
 $$ \begin{align*}M_{\phi}=\left( \begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & h_2 & 1 & 0 & 0 & 0 \\ 0 & h_3 & 2h_2 & 1 & 0 & 0 \\ 0 & h_4 & 2h_3+h_2^2 & 3h_2 & 1 & 0 \\ 0 & h_5 & 2b_4+2h_2h_3 & 3h_3+3h_2^2 & 4h_2 & 1 \\ \end{array} \right). \end{align*} $$
$$ \begin{align*}M_{\phi}=\left( \begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & h_2 & 1 & 0 & 0 & 0 \\ 0 & h_3 & 2h_2 & 1 & 0 & 0 \\ 0 & h_4 & 2h_3+h_2^2 & 3h_2 & 1 & 0 \\ 0 & h_5 & 2b_4+2h_2h_3 & 3h_3+3h_2^2 & 4h_2 & 1 \\ \end{array} \right). \end{align*} $$
Then the matrix of the isomorphism
![]() $\phi ^*:B_2^{\perp }\longrightarrow B_1^{\perp }$
with respect to
$\phi ^*:B_2^{\perp }\longrightarrow B_1^{\perp }$
with respect to
![]() $\frac {1}{i!} u^i$
,
$\frac {1}{i!} u^i$
,
![]() $i=0,\dots , 5$
, is
$i=0,\dots , 5$
, is
![]() $M_{\phi }^\tau $
. Since
$M_{\phi }^\tau $
. Since
![]() $B_1$
is the monomial
$B_1$
is the monomial
![]() ${\mathbf {k}}$
-algebra
${\mathbf {k}}$
-algebra
![]() ${\mathbf {k}}[\![t^2,t^7]\!]$
, the
${\mathbf {k}}[\![t^2,t^7]\!]$
, the
![]() ${\mathbf {k}}$
-vector space
${\mathbf {k}}$
-vector space
![]() $B_1^{\perp }$
is generated by
$B_1^{\perp }$
is generated by
![]() $u, u^3, u^5$
. From this, we can compute
$u, u^3, u^5$
. From this, we can compute
![]() $B_2^{\perp }$
by considering
$B_2^{\perp }$
by considering
![]() $(^\tau M_{\phi })^{-1}$
.
$(^\tau M_{\phi })^{-1}$
.
4 Algebra-forming vector spaces
The first goal of this section is to characterize the algebra-forming
![]() ${\mathbf {k}}$
-vector spaces.
${\mathbf {k}}$
-vector spaces.
Proposition 4.1 Let B be a
![]() ${\mathbf {k}}$
-sub-algebra of finite codimension of
${\mathbf {k}}$
-sub-algebra of finite codimension of
![]() $\Gamma $
with conductor c, and let
$\Gamma $
with conductor c, and let
![]() $f_1,\dots , f_s$
be a system of generators of B. Given an integer
$f_1,\dots , f_s$
be a system of generators of B. Given an integer
![]() $d\ge c-1$
, let
$d\ge c-1$
, let
![]() $h_1,\dots , h_m$
be a system of generators of
$h_1,\dots , h_m$
be a system of generators of
![]() $W(\{f_1,\dots , f_s\},d)$
.
$W(\{f_1,\dots , f_s\},d)$
.
Let V be a dimension
![]() $\delta $
$\delta $
![]() ${\mathbf {k}}$
-vector subspace of
${\mathbf {k}}$
-vector subspace of
![]() $(u)\subset \Delta $
generated by polynomials of degree at most
$(u)\subset \Delta $
generated by polynomials of degree at most
![]() $d-1$
. Let
$d-1$
. Let
![]() $g_1,\dots ,g_{\delta }\in V$
be a basis of V.
$g_1,\dots ,g_{\delta }\in V$
be a basis of V.
Then V is algebra-forming with respect to B iff for all r-upla
![]() $(\lambda _1,\dots ,\lambda _m)\in {\mathbf {k}}^m$
such that
$(\lambda _1,\dots ,\lambda _m)\in {\mathbf {k}}^m$
such that
 $$ \begin{align} \sum_{j=1}^m \lambda_j (g_i\perp h_j)=0 \end{align} $$
$$ \begin{align} \sum_{j=1}^m \lambda_j (g_i\perp h_j)=0 \end{align} $$
for all
![]() $i=1,\dots ,\delta $
, then
$i=1,\dots ,\delta $
, then
 $$ \begin{align} \sum_{j=1}^m \lambda_j^2 (g_i\perp h_j^2)+ 2 \sum_{j=1,l=1,j\neq l}^m \lambda_j \lambda_j (g_i\perp h_j h_l)=0 \end{align} $$
$$ \begin{align} \sum_{j=1}^m \lambda_j^2 (g_i\perp h_j^2)+ 2 \sum_{j=1,l=1,j\neq l}^m \lambda_j \lambda_j (g_i\perp h_j h_l)=0 \end{align} $$
for all
![]() $i=1,\dots ,\delta $
.
$i=1,\dots ,\delta $
.
Proof From Proposition 3.2, we have to prove that for all
![]() $f\in B$
such that
$f\in B$
such that
![]() $g\perp f=0$
for all
$g\perp f=0$
for all
![]() $g\in V$
we have that
$g\in V$
we have that
![]() $g\perp f^2=0$
for all
$g\perp f^2=0$
for all
![]() $g\in V$
. Since the polynomials of V are of degree at most
$g\in V$
. Since the polynomials of V are of degree at most
![]() $d-1$
we only have to prove that for all
$d-1$
we only have to prove that for all
![]() $f\in W=W(\{f_1,\dots , f_s\},d)$
such that
$f\in W=W(\{f_1,\dots , f_s\},d)$
such that
![]() $g\perp f=0$
for all
$g\perp f=0$
for all
![]() $g\in V$
, we have that
$g\in V$
, we have that
![]() $g\perp f^2=0$
for all
$g\perp f^2=0$
for all
![]() $g\in V$
.
$g\in V$
.
A general element of W can be written as
![]() $f=\sum _{j=1}^m \lambda _j h_j$
. Hence the condition
$f=\sum _{j=1}^m \lambda _j h_j$
. Hence the condition
![]() $g_i\perp f=0$
is equivalent to
$g_i\perp f=0$
is equivalent to
 $$ \begin{align*}\sum_{j=1}^m \lambda_j (g_i\perp h_j)=0 \end{align*} $$
$$ \begin{align*}\sum_{j=1}^m \lambda_j (g_i\perp h_j)=0 \end{align*} $$
for all
![]() $i=1,\dots ,\delta $
. Similarly, the condition
$i=1,\dots ,\delta $
. Similarly, the condition
![]() $g_i\perp f^2=0$
is equivalent to
$g_i\perp f^2=0$
is equivalent to
 $$ \begin{align*}\sum_{j=1}^m \lambda_j^2 (g_i\perp h_j^2)+ 2 \sum_{j=1,l=1,j\neq l}^m \lambda_j \lambda_j (g_i\perp h_j h_l)=0 \end{align*} $$
$$ \begin{align*}\sum_{j=1}^m \lambda_j^2 (g_i\perp h_j^2)+ 2 \sum_{j=1,l=1,j\neq l}^m \lambda_j \lambda_j (g_i\perp h_j h_l)=0 \end{align*} $$
for all
![]() $i=1,\dots ,\delta $
.
$i=1,\dots ,\delta $
.
Remark 4.2 The set of points
![]() $(\lambda _1,\dots ,\lambda _m)\in \mathbb P^{m-1}_{{\mathbf {k}}}$
satisfying the identities of (3) form a linear subvariety L, and the points satisfying the identities of (4) defines a subvariety
$(\lambda _1,\dots ,\lambda _m)\in \mathbb P^{m-1}_{{\mathbf {k}}}$
satisfying the identities of (3) form a linear subvariety L, and the points satisfying the identities of (4) defines a subvariety
![]() $Q\subset \mathbb P^{m-1}_{{\mathbf {k}}}$
intersection of
$Q\subset \mathbb P^{m-1}_{{\mathbf {k}}}$
intersection of
![]() $\delta $
quadrics. Hence, V is algebra forming with respect to B iff
$\delta $
quadrics. Hence, V is algebra forming with respect to B iff
![]() $L\subset Q$
. This is a computable condition.
$L\subset Q$
. This is a computable condition.
Definition 4.3 Let B be a sub-
![]() ${\mathbf {k}}$
-algebra of finite codimension
${\mathbf {k}}$
-algebra of finite codimension
![]() $\delta $
of
$\delta $
of
![]() $\Gamma $
and conductor c. Let D be the semigroup of B; we write the set
$\Gamma $
and conductor c. Let D be the semigroup of B; we write the set
![]() $t^{\mathbb N\setminus D_B}=\{t^i; i\in \mathbb N\setminus D_B \}$
as
$t^{\mathbb N\setminus D_B}=\{t^i; i\in \mathbb N\setminus D_B \}$
as
![]() $g_1=t^{c-1},\dots , g_{\delta }=t$
. Then we define the so-called standard filtration of B as follows:
$g_1=t^{c-1},\dots , g_{\delta }=t$
. Then we define the so-called standard filtration of B as follows:
![]() $B_i$
is the
$B_i$
is the
![]() ${\mathbf {k}}$
-algebra generated by B and
${\mathbf {k}}$
-algebra generated by B and
![]() $g_1,\dots , g_i$
for
$g_1,\dots , g_i$
for
![]() $i=1, \dots , \delta $
; we set
$i=1, \dots , \delta $
; we set
![]() $B_0=B$
. Notice that
$B_0=B$
. Notice that
![]() $B_{\delta }=\Gamma $
and that we have
$B_{\delta }=\Gamma $
and that we have
and
![]() $\operatorname {dim}_{{\mathbf {k}}}(B_{i+1}/B_i)=1$
,
$\operatorname {dim}_{{\mathbf {k}}}(B_{i+1}/B_i)=1$
,
![]() $i=0,\dots , \delta -1$
.
$i=0,\dots , \delta -1$
.
After the definition of standard filtration, we only have to consider algebra-forming elements
![]() $g\in \Delta $
, with respect a suitable sub-
$g\in \Delta $
, with respect a suitable sub-
![]() ${\mathbf {k}}$
-algebras of
${\mathbf {k}}$
-algebras of
![]() $\Gamma $
, in order to define a
$\Gamma $
, in order to define a
![]() ${\mathbf {k}}$
-algebra recursively. The algebra-forming elements are not unique as the following example shows.
${\mathbf {k}}$
-algebra recursively. The algebra-forming elements are not unique as the following example shows.
Example 4.4 Let us consider the Example 3.7. The standard filtration of B is
The chain of
![]() ${\mathbf {k}}$
-algebras is defined as follows. The cosets of
${\mathbf {k}}$
-algebras is defined as follows. The cosets of
![]() $t,t^2, t^4, t^7$
in
$t,t^2, t^4, t^7$
in
![]() $\Gamma /B$
form a basis of
$\Gamma /B$
form a basis of
![]() $\Gamma /B$
as
$\Gamma /B$
as
![]() ${\mathbf {k}}$
-vector space. Then
${\mathbf {k}}$
-vector space. Then
![]() $B_1$
is the
$B_1$
is the
![]() ${\mathbf {k}}$
-algebra generated by B and
${\mathbf {k}}$
-algebra generated by B and
![]() $t^7$
,
$t^7$
,
![]() $B_2$
is the
$B_2$
is the
![]() ${\mathbf {k}}$
-algebra generated by
${\mathbf {k}}$
-algebra generated by
![]() $B_1$
and
$B_1$
and
![]() $t^4$
,
$t^4$
,
![]() $B_3$
is the
$B_3$
is the
![]() ${\mathbf {k}}$
-algebra generated by B and
${\mathbf {k}}$
-algebra generated by B and
![]() $t^2$
, and finally
$t^2$
, and finally
![]() $\Gamma $
is the
$\Gamma $
is the
![]() ${\mathbf {k}}$
-algebra generated by B and t.
${\mathbf {k}}$
-algebra generated by B and t.
We know that
![]() $B^{\perp }$
is a four-dimensional
$B^{\perp }$
is a four-dimensional
![]() ${\mathbf {k}}$
-vector space generated by
${\mathbf {k}}$
-vector space generated by
![]() $u, u^2, u^3-\frac {1}{4}u^4, u^6-\frac {1}{2.7}u^7$
; we have
$u, u^2, u^3-\frac {1}{4}u^4, u^6-\frac {1}{2.7}u^7$
; we have
![]() $B_3=\operatorname {Ann}\langle u\rangle $
,
$B_3=\operatorname {Ann}\langle u\rangle $
,
![]() $B_2=\operatorname {Ann}\langle u^2\rangle \cap B_3$
,
$B_2=\operatorname {Ann}\langle u^2\rangle \cap B_3$
,
![]() $B_1=\operatorname {Ann}\langle u^3-\frac {1}{4}u^4\rangle \cap B_2$
,
$B_1=\operatorname {Ann}\langle u^3-\frac {1}{4}u^4\rangle \cap B_2$
,
![]() $B=\operatorname {Ann}\langle u^6-\frac {1}{2.7}u^7\rangle \cap B_1$
. On the other hand, the
$B=\operatorname {Ann}\langle u^6-\frac {1}{2.7}u^7\rangle \cap B_1$
. On the other hand, the
![]() ${\mathbf {k}}$
-algebra
${\mathbf {k}}$
-algebra
![]() $C_1={\mathbf {k}}[\![t^3+t^5,t^4]\!]\subset B_1$
can be obtained as
$C_1={\mathbf {k}}[\![t^3+t^5,t^4]\!]\subset B_1$
can be obtained as
i.e.,
![]() $u^3-\frac {1}{4.5}u^5$
is an algebra-forming element with respect to
$u^3-\frac {1}{4.5}u^5$
is an algebra-forming element with respect to
![]() $B_2$
. Notice that
$B_2$
. Notice that
![]() $B_1$
and
$B_1$
and
![]() $C_1$
are non analytically isomorphic codimension one
$C_1$
are non analytically isomorphic codimension one
![]() ${\mathbf {k}}$
-algebras of
${\mathbf {k}}$
-algebras of
![]() $B_2$
.
$B_2$
.
Next, we show how to build the standard filtration by using derivations.
Proposition 4.5 Let
![]() $C\subset B$
be two sub-
$C\subset B$
be two sub-
![]() ${\mathbf {k}}$
-algebras of
${\mathbf {k}}$
-algebras of
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $\operatorname {dim}_{{\mathbf {k}}}(B/C)=1$
. There exist
$\operatorname {dim}_{{\mathbf {k}}}(B/C)=1$
. There exist
![]() $\alpha \in Der_{{\mathbf {k}}}(B)$
such that
$\alpha \in Der_{{\mathbf {k}}}(B)$
such that
![]() $\ker (\alpha )=C$
.
$\ker (\alpha )=C$
.
Proof If we denote by
![]() $\max _B$
, the maximal ideal of B then
$\max _B$
, the maximal ideal of B then
![]() $\max _C\subset \max _B$
,
$\max _C\subset \max _B$
,
![]() $\operatorname {dim}_{{\mathbf {k}}}(\max _B/\max _C)=1$
and
$\operatorname {dim}_{{\mathbf {k}}}(\max _B/\max _C)=1$
and
![]() $\max _B^2\subset \max _C$
. Since we have
$\max _B^2\subset \max _C$
. Since we have
we deduce that there exists a linear form
![]() $\alpha : \frac {\max _B}{\max _B^2}\longrightarrow {\mathbf {k}}$
such that
$\alpha : \frac {\max _B}{\max _B^2}\longrightarrow {\mathbf {k}}$
such that
![]() $\ker (\alpha )=\frac {\max _C}{\max _B^2}$
. From this, we get the claim.
$\ker (\alpha )=\frac {\max _C}{\max _B^2}$
. From this, we get the claim.
Corollary 4.6 Let B be a sub-
![]() ${\mathbf {k}}$
-algebra of finite codimension
${\mathbf {k}}$
-algebra of finite codimension
![]() $\delta $
of
$\delta $
of
![]() $\Gamma $
. Let us consider the standard filtration of B:
$\Gamma $
. Let us consider the standard filtration of B:
For all
![]() $i=1,\dots ,\delta ,$
there exists a derivation
$i=1,\dots ,\delta ,$
there exists a derivation
![]() $\partial _{l_i}\in Der_{{\mathbf {k}}}(B_i)$
,
$\partial _{l_i}\in Der_{{\mathbf {k}}}(B_i)$
,
![]() $l_i\in \max _{B_i}$
, such that
$l_i\in \max _{B_i}$
, such that
![]() $\ker (\partial _{l_i})=B_i$
.
$\ker (\partial _{l_i})=B_i$
.
Example 4.7 Let us consider the Example 4.4. The element
![]() $u^{\perp }$
corresponds to the derivation
$u^{\perp }$
corresponds to the derivation
![]() $\partial _t$
of
$\partial _t$
of
![]() $\Gamma $
defined by t, so
$\Gamma $
defined by t, so
![]() $B_3=\ker (\partial _t)$
. The maximal ideal of
$B_3=\ker (\partial _t)$
. The maximal ideal of
![]() $B_3$
is minimally generated by
$B_3$
is minimally generated by
![]() $t^2, t^3$
, the element
$t^2, t^3$
, the element
![]() $(u^2)^\perp $
is the derivation
$(u^2)^\perp $
is the derivation
![]() $\partial _{t^2}\in Der_{{\mathbf {k}}}(B_3)$
, so
$\partial _{t^2}\in Der_{{\mathbf {k}}}(B_3)$
, so
![]() ${B_2=\ker (\partial _{t^2})}$
. The maximal ideal of
${B_2=\ker (\partial _{t^2})}$
. The maximal ideal of
![]() $B_2$
is minimally generated by
$B_2$
is minimally generated by
![]() $t^3, t^4, t^5$
. The element
$t^3, t^4, t^5$
. The element
![]() $(u^3-\frac {1}{4}u^4)^{\perp }$
is the derivation
$(u^3-\frac {1}{4}u^4)^{\perp }$
is the derivation
![]() $\partial _{t^3-\frac {1}{4}t^4}\in Der_{{\mathbf {k}}}(B_2)$
, so
$\partial _{t^3-\frac {1}{4}t^4}\in Der_{{\mathbf {k}}}(B_2)$
, so
![]() $B_1=\ker (\partial _{t^3-\frac {1}{4}t^4})$
. Finally,
$B_1=\ker (\partial _{t^3-\frac {1}{4}t^4})$
. Finally,
![]() $\partial _{t^7}\in Der_{{\mathbf {k}}}(B_1)$
and
$\partial _{t^7}\in Der_{{\mathbf {k}}}(B_1)$
and
![]() $B=\ker (\partial _{t^7})$
.
$B=\ker (\partial _{t^7})$
.
5 Monomial algebras
In this section, we first compute the inverse system of a monomial
![]() ${\mathbf {k}}$
-algebra. After this, we characterize monomial Gorenstein curve singularities in terms of its inverse system. We end the section relating the inverse system of a curve singularity with its generic plane projection and its saturation.
${\mathbf {k}}$
-algebra. After this, we characterize monomial Gorenstein curve singularities in terms of its inverse system. We end the section relating the inverse system of a curve singularity with its generic plane projection and its saturation.
The following result it is easy to deduce from the proof of the second part of Proposition 3.2(2).
Proposition 5.1 Let D be an additive sub-semigroup of
![]() $\mathbb N$
with finite complement. Then
$\mathbb N$
with finite complement. Then
![]() $B^{\perp }$
is the
$B^{\perp }$
is the
![]() ${\mathbf {k}}$
-vector space generated by:
${\mathbf {k}}$
-vector space generated by:
![]() $g_i=u^i$
for
$g_i=u^i$
for
![]() $i\in \mathbb N\setminus D$
.
$i\in \mathbb N\setminus D$
.
Example 5.2 Let B be a sub-
![]() ${\mathbf {k}}$
-algebra of
${\mathbf {k}}$
-algebra of
![]() ${\mathbf {k}}[\![t]\!]$
of codimension
${\mathbf {k}}[\![t]\!]$
of codimension
![]() $\delta =1$
. Then B is the
$\delta =1$
. Then B is the
![]() ${\mathbf {k}}$
-algebra
${\mathbf {k}}$
-algebra
![]() $B={\mathbf {k}}[\![D]\!]$
, where D is the sub-semigroup of
$B={\mathbf {k}}[\![D]\!]$
, where D is the sub-semigroup of
![]() $\mathbb N$
generated by
$\mathbb N$
generated by
![]() $2, 3$
. Hence,
$2, 3$
. Hence,
![]() $B^{\perp }$
is the
$B^{\perp }$
is the
![]() ${\mathbf {k}}$
-vector space generated by u, i.e., B is the set of power series
${\mathbf {k}}$
-vector space generated by u, i.e., B is the set of power series
![]() $f=\sum _{i\ge 0} b_it^i \in {\mathbf {k}}[\![t]\!]$
with
$f=\sum _{i\ge 0} b_it^i \in {\mathbf {k}}[\![t]\!]$
with
![]() $u\perp f= b_1=0$
(see [Reference Serre26, Example b, Section 4 of Chapter IV] and [Reference Grönkvist, Leffler, Torstensson and Ufnarovski18, Section 22]).
$u\perp f= b_1=0$
(see [Reference Serre26, Example b, Section 4 of Chapter IV] and [Reference Grönkvist, Leffler, Torstensson and Ufnarovski18, Section 22]).
Example 5.3 Assume now that B is sub-
![]() ${\mathbf {k}}$
-algebra of
${\mathbf {k}}$
-algebra of
![]() ${\mathbf {k}}[\![t]\!]$
of codimension
${\mathbf {k}}[\![t]\!]$
of codimension
![]() $\delta = 2$
. Then its semi-group
$\delta = 2$
. Then its semi-group
![]() $D_B$
is
$D_B$
is
![]() $D_1=\langle 2, 5\rangle $
or
$D_1=\langle 2, 5\rangle $
or
![]() $D_2=\langle 3, 4\rangle $
. In the first case, B is generated as
$D_2=\langle 3, 4\rangle $
. In the first case, B is generated as
![]() ${\mathbf {k}}$
-algebra by
${\mathbf {k}}$
-algebra by
![]() $f_1=t^2+b_3 t^3$
and
$f_1=t^2+b_3 t^3$
and
![]() $f_2=t^5$
. The conductor is
$f_2=t^5$
. The conductor is
![]() $c=4$
. Then
$c=4$
. Then
![]() $B^{\perp }$
is generated by
$B^{\perp }$
is generated by
![]() $g_1=u$
,
$g_1=u$
,
![]() $g_2=6 b_3 u^2 +u^3$
. In the second case, B is the monomial
$g_2=6 b_3 u^2 +u^3$
. In the second case, B is the monomial
![]() ${\mathbf {k}}$
-algebra
${\mathbf {k}}$
-algebra
![]() $B={\mathbf {k}}[\![D_2]\!]$
so
$B={\mathbf {k}}[\![D_2]\!]$
so
![]() $B^{\perp }$
is the sub-
$B^{\perp }$
is the sub-
![]() ${\mathbf {k}}$
-algebra generated by
${\mathbf {k}}$
-algebra generated by
![]() $g_1=u$
and
$g_1=u$
and
![]() $g_2=u^2$
. The conductor is
$g_2=u^2$
. The conductor is
![]() $c=5$
(see [Reference Grönkvist, Leffler, Torstensson and Ufnarovski18, Section 23]). It is known that the algebras of the first case are all analytically isomorphic to
$c=5$
(see [Reference Grönkvist, Leffler, Torstensson and Ufnarovski18, Section 23]). It is known that the algebras of the first case are all analytically isomorphic to
![]() ${\mathbf {k}}[\![D_1]\!]$
.
${\mathbf {k}}[\![D_1]\!]$
.
The inverse system of a monomial Gorenstein
![]() ${\mathbf {k}}$
-algebra case can be handled. Let us recall the definition of symmetric semi-group and the celebrate result of Kunz.
${\mathbf {k}}$
-algebra case can be handled. Let us recall the definition of symmetric semi-group and the celebrate result of Kunz.
Definition 5.4 We say that a sub-semigroup D of
![]() $\mathbb N$
such that
$\mathbb N$
such that
![]() $\#(\mathbb N \setminus D)<\infty $
and with conductor c is symmetric if the condition
$\#(\mathbb N \setminus D)<\infty $
and with conductor c is symmetric if the condition
![]() $t\in D$
is equivalent to
$t\in D$
is equivalent to
![]() $c-1-t\notin D$
.
$c-1-t\notin D$
.
Kunz proved that the ring
![]() ${\mathbf {k}}[\![D]\!]$
is Gorenstein ring if and only if D is a symmetric semigroup,[Reference Kunz21]. This symmetry is inherited by
${\mathbf {k}}[\![D]\!]$
is Gorenstein ring if and only if D is a symmetric semigroup,[Reference Kunz21]. This symmetry is inherited by
![]() $B^{\perp }$
.
$B^{\perp }$
.
Proposition 5.5 Let D be a sub-semigroup of
![]() $\mathbb N$
such that
$\mathbb N$
such that
![]() $\#(\mathbb N \setminus D)<\infty $
and conductor c. The following conditions are equivalent:
$\#(\mathbb N \setminus D)<\infty $
and conductor c. The following conditions are equivalent:
-
(1)
 ${\mathbf {k}}[\![D]\!]$
is Gorenstein,
${\mathbf {k}}[\![D]\!]$
is Gorenstein, -
(2) for all
 $g\in {\mathbf {k}}[\![D]\!]^{\perp }$
it holds
$g\in {\mathbf {k}}[\![D]\!]^{\perp }$
it holds
 $t^{c-1} g(1/t)\in {\mathbf {k}}[\![D]\!]$
.
$t^{c-1} g(1/t)\in {\mathbf {k}}[\![D]\!]$
.
Proof Since
![]() $B={\mathbf {k}}[\![D]\!]$
is a monomial
$B={\mathbf {k}}[\![D]\!]$
is a monomial
![]() ${\mathbf {k}}$
-algebra we know that
${\mathbf {k}}$
-algebra we know that
![]() $B^{\perp }$
is generated by
$B^{\perp }$
is generated by
![]() $g=\sum _{i=1}^{c-1}a_i u^i$
such that
$g=\sum _{i=1}^{c-1}a_i u^i$
such that
![]() $a_i=0$
for
$a_i=0$
for
![]() $i\in D$
(see Proposition 5.1). Then the exponents of the nonzero terms of
$i\in D$
(see Proposition 5.1). Then the exponents of the nonzero terms of
![]() $t^{c-1} g(1/t)$
are
$t^{c-1} g(1/t)$
are
![]() $c-1-i$
with
$c-1-i$
with
![]() $i\notin D$
. Then the claim is equivalent to the symmetry of D, i.e., the Gorensteinness of B.
$i\notin D$
. Then the claim is equivalent to the symmetry of D, i.e., the Gorensteinness of B.
Example 5.6 Let D be the semigroup generated by
![]() $4, 6 ,$
and
$4, 6 ,$
and
![]() $ 9$
. This is a symmetric semigroup with conductor
$ 9$
. This is a symmetric semigroup with conductor
![]() $c=12$
. The algebra
$c=12$
. The algebra
![]() $B={\mathbf {k}}[\![D]\!]$
is Gorenstein and isomorphic to
$B={\mathbf {k}}[\![D]\!]$
is Gorenstein and isomorphic to
![]() ${\mathbf {k}}[\![x,y,z]\!]/I$
, where
${\mathbf {k}}[\![x,y,z]\!]/I$
, where
![]() $I=(x^3-y^2, y^3-z^2)$
. Then
$I=(x^3-y^2, y^3-z^2)$
. Then
![]() $B^{\perp }$
is generated by the polynomials
$B^{\perp }$
is generated by the polynomials
![]() $g=a_1 u+ a_2 u^2+ a_3 u^3 + a_5 u^5 + a_7 u^7$
,
$g=a_1 u+ a_2 u^2+ a_3 u^3 + a_5 u^5 + a_7 u^7$
,
![]() $a_i\in {\mathbf {k}}$
. The polynomials
$a_i\in {\mathbf {k}}$
. The polynomials
![]() $t^{11}g(1/t)= a_1 t^{10}+ a_2 t^9 + a_3 u^8 + a_4 u^6+a_5 u^4$
have all exponents in D. The
$t^{11}g(1/t)= a_1 t^{10}+ a_2 t^9 + a_3 u^8 + a_4 u^6+a_5 u^4$
have all exponents in D. The
![]() ${\mathbf {k}}$
-vector space
${\mathbf {k}}$
-vector space
![]() $B^{\perp }$
is generated by the following elements
$B^{\perp }$
is generated by the following elements
![]() $g_1=u, g_2=u^2, g_3=u^3, g_4=u^5, g_5=u^7$
.
$g_1=u, g_2=u^2, g_3=u^3, g_4=u^5, g_5=u^7$
.
Given a finite codimension subalgebra B of
![]() $\Gamma $
, we consider the curve singularity
$\Gamma $
, we consider the curve singularity
![]() $X=\operatorname {Spec}(B)$
defined by B. Let
$X=\operatorname {Spec}(B)$
defined by B. Let
![]() $X'$
be the generic plane projection of X, [Reference Briançon, Galligo and Granger3], and let
$X'$
be the generic plane projection of X, [Reference Briançon, Galligo and Granger3], and let
![]() $\widetilde {X}$
be the saturation of X, [Reference Zariski28] and the references therein. We have
$\widetilde {X}$
be the saturation of X, [Reference Zariski28] and the references therein. We have
and then
We have, [Reference Elias9],
From [Reference Zariski27, Proposition 1.6, page 971], we know that
![]() $\widetilde {X}$
is also the saturation of
$\widetilde {X}$
is also the saturation of
![]() $X'$
.
$X'$
.
On the other hand,
![]() $\widetilde {X}$
is a monomial curve singularity. Assume that the coset of
$\widetilde {X}$
is a monomial curve singularity. Assume that the coset of
![]() $x_1$
in B is
$x_1$
in B is
![]() $t^{e_0}$
with
$t^{e_0}$
with
![]() $e_0$
the multiplicity of B. Since the rings are complete and the ground field is algebraically closed, we can assumed it after a suitable election of the uniformization parameter of
$e_0$
the multiplicity of B. Since the rings are complete and the ground field is algebraically closed, we can assumed it after a suitable election of the uniformization parameter of
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $\{e_0; \beta _1,\dots , \beta _g\}$
be the characteristic of
$\{e_0; \beta _1,\dots , \beta _g\}$
be the characteristic of
![]() $X'$
, [Reference Zariski28, Section 3, page 993], then
$X'$
, [Reference Zariski28, Section 3, page 993], then
![]() ${\mathcal O}_{\widetilde {X}}$
is the monomial subalgebra with generators:
${\mathcal O}_{\widetilde {X}}$
is the monomial subalgebra with generators:
 $$ \begin{align*}\left\{ \begin{array}{ll} t^{e_0}, & \mbox{} \\ t^{s_\nu n_{\nu+1}\dots n_g}, & \mbox{} m_{\nu}\le s_{\nu}\le [m_{\nu+1}/n_{\nu+1}], \nu=1,\dots, g-1, \\ t^{m_g+i}, & \mbox{} 0\le i\le e_0-1, \end{array} \right. \end{align*} $$
$$ \begin{align*}\left\{ \begin{array}{ll} t^{e_0}, & \mbox{} \\ t^{s_\nu n_{\nu+1}\dots n_g}, & \mbox{} m_{\nu}\le s_{\nu}\le [m_{\nu+1}/n_{\nu+1}], \nu=1,\dots, g-1, \\ t^{m_g+i}, & \mbox{} 0\le i\le e_0-1, \end{array} \right. \end{align*} $$
where
![]() $\beta _{\nu }/e_0=m_{\nu }/n_1\dots n_{\nu }$
is the
$\beta _{\nu }/e_0=m_{\nu }/n_1\dots n_{\nu }$
is the
![]() $\nu $
th characteristic exponent of
$\nu $
th characteristic exponent of
![]() $X'$
,
$X'$
,
![]() $\nu =1,\dots , g-1$
, and
$\nu =1,\dots , g-1$
, and
![]() $\gcd (m_i, n_i)=1$
for all
$\gcd (m_i, n_i)=1$
for all
![]() $i=1,\dots ,g$
(see [Reference Zariski28, Section 3, page 995]).
$i=1,\dots ,g$
(see [Reference Zariski28, Section 3, page 995]).
The facts
![]() ${\mathcal O}_{\widetilde {X}}^{\perp }\subset B^{\perp }$
and Proposition 5.2 can be useful in order to simplify the computation of
${\mathcal O}_{\widetilde {X}}^{\perp }\subset B^{\perp }$
and Proposition 5.2 can be useful in order to simplify the computation of
![]() $B^{\perp }$
as the next example shows.
$B^{\perp }$
as the next example shows.
Example 5.7 Let us consider the
![]() ${\mathbf {k}}$
-algebra
${\mathbf {k}}$
-algebra
![]() $B={\mathbf {k}}[\![t^6, t^8+t^{11}, t^{10}+t^{13} ]\!]$
; its saturation is
$B={\mathbf {k}}[\![t^6, t^8+t^{11}, t^{10}+t^{13} ]\!]$
; its saturation is
![]() $\widetilde {B}={\mathbf {k}}[\![t^6, t^8, t^{10}, t^{11}, t^{13}, t^{15}]\!]$
(see [Reference Campillo and Castellanos6, Example 2.5.1]). The sequence of multiplicities of the resolution of
$\widetilde {B}={\mathbf {k}}[\![t^6, t^8, t^{10}, t^{11}, t^{13}, t^{15}]\!]$
(see [Reference Campillo and Castellanos6, Example 2.5.1]). The sequence of multiplicities of the resolution of
![]() $X=\operatorname {Spec}(B)$
is
$X=\operatorname {Spec}(B)$
is
![]() $\{6,2,2,2,2,1,\dots \}$
. We can compute
$\{6,2,2,2,2,1,\dots \}$
. We can compute
![]() $\delta (X)$
by computing
$\delta (X)$
by computing
![]() $e_1(C),$
where C ranges the local rings of the resolution process, in this case, we get
$e_1(C),$
where C ranges the local rings of the resolution process, in this case, we get
![]() $\{8,1,1,1,1,0,\dots \}$
, so
$\{8,1,1,1,1,0,\dots \}$
, so
![]() $\delta (X)=12$
. The semigroup of B is
$\delta (X)=12$
. The semigroup of B is
![]() $D=\{0,6,8,10,12,14,16,18,19,20,22\rightarrow \}$
, i.e., the conductor of D is
$D=\{0,6,8,10,12,14,16,18,19,20,22\rightarrow \}$
, i.e., the conductor of D is
![]() $22$
.
$22$
.
On the other hand, the semigroup of
![]() ${\mathcal O}_{\widetilde {X}}$
is
${\mathcal O}_{\widetilde {X}}$
is
![]() $\{0,6,8,10\longrightarrow \}$
, its conductor is
$\{0,6,8,10\longrightarrow \}$
, its conductor is
![]() $10$
. Hence,
$10$
. Hence,
![]() ${\mathcal O}_{\widetilde {X}}^{\perp }$
is generated by
${\mathcal O}_{\widetilde {X}}^{\perp }$
is generated by
![]() $u^i$
with
$u^i$
with
![]() $i\in \{1,2,3,4,5,7,9\}$
, and
$i\in \{1,2,3,4,5,7,9\}$
, and
![]() $B^{\perp }$
is the set of polynomials
$B^{\perp }$
is the set of polynomials
![]() $g=\sum _{i=0}^{21} a_i u^i$
such that
$g=\sum _{i=0}^{21} a_i u^i$
such that
![]() $a_6=0$
,
$a_6=0$
,
![]() $990 a_{11}- a_8=0$
,
$990 a_{11}- a_8=0$
,
![]() $a_{12}=0$
,
$a_{12}=0$
,
![]() $1716 a_{13}-a_{10}=0$
,
$1716 a_{13}-a_{10}=0$
,
![]() $a_{16}=0$
,
$a_{16}=0$
,
![]() $4080 a_{17}-a_{14}=0$
,
$4080 a_{17}-a_{14}=0$
,
![]() $a_{18}=a_{19}=a_{20}=a_{21}=0$
.
$a_{18}=a_{19}=a_{20}=a_{21}=0$
.
6 The canonical module
As in the Artin case, we can relate the canonical module with the inverse system. In that case, we have that if I is an Artinian ideal, then
![]() $I^{\perp }\cong E_{R/I}({\mathbf {k}})\cong \omega _{R/I}$
(see [Reference Bruns and Herzog4, Reference Elias, Cuong, Hoa and Trung14]). In the case of branches, we can determine the “negative” part of the canonical module.
$I^{\perp }\cong E_{R/I}({\mathbf {k}})\cong \omega _{R/I}$
(see [Reference Bruns and Herzog4, Reference Elias, Cuong, Hoa and Trung14]). In the case of branches, we can determine the “negative” part of the canonical module.
Let X be a branch of
![]() $({\mathbf {k}}^n,0)$
and
$({\mathbf {k}}^n,0)$
and
![]() $\overline {X}$
its normalization. We first describe the canonical module
$\overline {X}$
its normalization. We first describe the canonical module
![]() $\omega _X$
by using Rosenlicht’s regular differential forms (see [Reference Serre26, Chapter IV 9], [Reference Buchweitz and Greuel5, Section 1], see also [Reference Elias13]). We denote by
$\omega _X$
by using Rosenlicht’s regular differential forms (see [Reference Serre26, Chapter IV 9], [Reference Buchweitz and Greuel5, Section 1], see also [Reference Elias13]). We denote by
![]() $\Omega _{\overline {X}}(p),$
the set of meromorphic forms in
$\Omega _{\overline {X}}(p),$
the set of meromorphic forms in
![]() $\overline {X}$
with a pole at most in
$\overline {X}$
with a pole at most in
![]() $p=\nu ^{-1}(0)$
. Then Rosenlicht’s differential forms are defined as follows:
$p=\nu ^{-1}(0)$
. Then Rosenlicht’s differential forms are defined as follows:
![]() $\omega ^R_{X}$
is the set of
$\omega ^R_{X}$
is the set of
![]() $\nu _*(\alpha )$
,
$\nu _*(\alpha )$
,
![]() $\alpha \in \Omega _{\overline {X}}(p)$
, such that for all
$\alpha \in \Omega _{\overline {X}}(p)$
, such that for all
![]() $F\in {\mathcal O}_{X},$
$F\in {\mathcal O}_{X},$
Notice that we have a mapping that we also denote by
In [Reference Altman and Kleiman1, Chapter VIII], it is proved that
![]() $\omega _{X} \stackrel {\phi }{\cong } \omega _{X}^R$
and
$\omega _{X} \stackrel {\phi }{\cong } \omega _{X}^R$
and
![]() $d_R=\phi d$
, where
$d_R=\phi d$
, where
![]() $d: {\mathcal O}_{X} \longrightarrow \omega _{X}$
is the map defined in the Section 1. Since
$d: {\mathcal O}_{X} \longrightarrow \omega _{X}$
is the map defined in the Section 1. Since
![]() ${\mathcal O}_{X}$
is a one-dimensional reduced ring, we know that
${\mathcal O}_{X}$
is a one-dimensional reduced ring, we know that
![]() $\omega _{(X,0)}$
is a sub-
$\omega _{(X,0)}$
is a sub-
![]() ${\mathcal O}_{X}$
-module of
${\mathcal O}_{X}$
-module of
![]() $\mathrm {tot}({\mathcal O}_{X})$
(see [Reference Bruns and Herzog4, Proposition 3.3.18]). There is a perfect pairing, [Reference Serre26, Chapter IV],
$\mathrm {tot}({\mathcal O}_{X})$
(see [Reference Bruns and Herzog4, Proposition 3.3.18]). There is a perfect pairing, [Reference Serre26, Chapter IV],
 $$ \begin{align*}\begin{array}{ccccc} \frac{\nu_* {\mathcal O}_{\overline{X}}}{{\mathcal O}_{X}} & \times& \frac{\omega_{(X,0)}}{\nu_* \Omega_{\overline{X}}} & \stackrel{\eta}{\longrightarrow} & \mathbb C \\ F & \times & \alpha & \longrightarrow & {\mathrm{res}}_{p}(F \alpha) \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ccccc} \frac{\nu_* {\mathcal O}_{\overline{X}}}{{\mathcal O}_{X}} & \times& \frac{\omega_{(X,0)}}{\nu_* \Omega_{\overline{X}}} & \stackrel{\eta}{\longrightarrow} & \mathbb C \\ F & \times & \alpha & \longrightarrow & {\mathrm{res}}_{p}(F \alpha) \end{array} \end{align*} $$
notice that for all
![]() $\lambda \in R$
it holds
$\lambda \in R$
it holds
![]() $ \eta (\lambda F, \alpha )= {\mathrm {res}}_{p}(\lambda F \alpha )=\eta ( F, \lambda \alpha ). $
$ \eta (\lambda F, \alpha )= {\mathrm {res}}_{p}(\lambda F \alpha )=\eta ( F, \lambda \alpha ). $
Proposition 6.1 Let X be a branch of
![]() $({\mathbf {k}} ^n,0)$
and
$({\mathbf {k}} ^n,0)$
and
![]() $\overline {X}$
its normalization. Then we have an isomorphism of the
$\overline {X}$
its normalization. Then we have an isomorphism of the
![]() $\delta (X)$
dimensional
$\delta (X)$
dimensional
![]() ${\mathbf {k}}$
-vector spaces:
${\mathbf {k}}$
-vector spaces:
such that
![]() $\epsilon (g)$
is the coset defined by
$\epsilon (g)$
is the coset defined by
![]() $\alpha = \sum _{i=0}^{c-1} i! c_{i} t^{-i-1}$
, for all
$\alpha = \sum _{i=0}^{c-1} i! c_{i} t^{-i-1}$
, for all
![]() $g=\sum _{i=0}^{c-1} c_i u^i\in B^{\perp }$
.
$g=\sum _{i=0}^{c-1} c_i u^i\in B^{\perp }$
.
Proof We write
![]() $B={\mathcal O}_{X}$
,
$B={\mathcal O}_{X}$
,
![]() $\Gamma =\nu _* {\mathcal O}_{\overline {X}}$
, and
$\Gamma =\nu _* {\mathcal O}_{\overline {X}}$
, and
![]() $\Omega _{\overline {X}}= \Gamma dt$
. Then
$\Omega _{\overline {X}}= \Gamma dt$
. Then
![]() $\epsilon $
is the composition of the isomorphisms induced by the above two perfect pairings
$\epsilon $
is the composition of the isomorphisms induced by the above two perfect pairings
 $$ \begin{align*}B^{\perp} \overset{\epsilon_1}{\cong} \left(\frac{\Gamma}{B}\right)^* \overset{\epsilon_2}{\cong} \frac{\omega_{X}}{\nu_* \Omega_{\overline{X}}}. \end{align*} $$
$$ \begin{align*}B^{\perp} \overset{\epsilon_1}{\cong} \left(\frac{\Gamma}{B}\right)^* \overset{\epsilon_2}{\cong} \frac{\omega_{X}}{\nu_* \Omega_{\overline{X}}}. \end{align*} $$
Next, we describe both morphisms
![]() $\epsilon _1, \epsilon _2$
. Given
$\epsilon _1, \epsilon _2$
. Given
![]() $g\in B^{\perp }$
, we can write it as
$g\in B^{\perp }$
, we can write it as
so
![]() $\epsilon _1(g)$
is the linear form induced by
$\epsilon _1(g)$
is the linear form induced by
![]() $\xi :\Gamma ^*\longrightarrow {\mathbf {k}}$
defined by: if
$\xi :\Gamma ^*\longrightarrow {\mathbf {k}}$
defined by: if
![]() $f=\sum _{i\ge 0} a_i t^i\in \Gamma ,$
then
$f=\sum _{i\ge 0} a_i t^i\in \Gamma ,$
then
 $$ \begin{align*}\xi(f)=\sum_{i=0}^{c-1} i! a_i c_i. \end{align*} $$
$$ \begin{align*}\xi(f)=\sum_{i=0}^{c-1} i! a_i c_i. \end{align*} $$
On the other hand, every
![]() $\alpha \in \omega _X$
can be written as
$\alpha \in \omega _X$
can be written as
![]() $\alpha =t^n h(t) dt$
with
$\alpha =t^n h(t) dt$
with
![]() $n\in \mathbb Z$
and
$n\in \mathbb Z$
and
![]() $h(t)\in \Gamma $
an invertible series. From [Reference Elias13, Proposition 2.6], we get that
$h(t)\in \Gamma $
an invertible series. From [Reference Elias13, Proposition 2.6], we get that
![]() $\alpha = \sum _{i\ge -c} e_i t^i$
such that
$\alpha = \sum _{i\ge -c} e_i t^i$
such that
![]() $\mathrm {{res}}_0(\alpha F)=0$
for all
$\mathrm {{res}}_0(\alpha F)=0$
for all
![]() $f\in B$
. Given
$f\in B$
. Given
![]() $f=\sum _{i\ge 0} a_i t^i\in \Gamma $
, we have
$f=\sum _{i\ge 0} a_i t^i\in \Gamma $
, we have
 $$ \begin{align*}\mathrm{{res}}_0(f \alpha)= \sum_{i=0}^{c-1} a_i e_{-i-1} \end{align*} $$
$$ \begin{align*}\mathrm{{res}}_0(f \alpha)= \sum_{i=0}^{c-1} a_i e_{-i-1} \end{align*} $$
so
![]() $\epsilon _2^{-1}(\alpha )$
is the linear form induced by
$\epsilon _2^{-1}(\alpha )$
is the linear form induced by
![]() $\xi ':\Gamma ^*\longrightarrow {\mathbf {k}}$
defined by
$\xi ':\Gamma ^*\longrightarrow {\mathbf {k}}$
defined by
 $$ \begin{align*}\xi'(f)=\sum_{i=0}^{c-1} a_i e_{-i-1}. \end{align*} $$
$$ \begin{align*}\xi'(f)=\sum_{i=0}^{c-1} a_i e_{-i-1}. \end{align*} $$
From this, we deduce that
![]() $e_{-i-1}=i! c_i$
for
$e_{-i-1}=i! c_i$
for
![]() $i=0,\dots , c-1$
.
$i=0,\dots , c-1$
.
Example 6.2 [Reference Elias13, Example 2.7]
Let us consider the monomial curve X with parameterization
![]() $x_1=t^4, x_2=t^7, x_3=t^9$
. We have
$x_1=t^4, x_2=t^7, x_3=t^9$
. We have
![]() $c=11$
,
$c=11$
,
![]() $\delta = 6$
. Then
$\delta = 6$
. Then
![]() $\omega _X$
is the
$\omega _X$
is the
![]() ${\mathbf {k}}$
-vector space spanned by
${\mathbf {k}}$
-vector space spanned by
![]() $t^{-11}, t^{-7}, t^{-6}, t^{-4}, t^{-3}, t^{-2}, t^n, n\ge 0$
, and the quotient
$t^{-11}, t^{-7}, t^{-6}, t^{-4}, t^{-3}, t^{-2}, t^n, n\ge 0$
, and the quotient
![]() $\omega _X/ \nu _* \Omega _{\overline {X}}$
admits as
$\omega _X/ \nu _* \Omega _{\overline {X}}$
admits as
![]() ${\mathbf {k}}$
-vector space base the cosets of
${\mathbf {k}}$
-vector space base the cosets of
![]() $t^{-11}, t^{-7}, t^{-6}, t^{-4}, t^{-3}$
,
$t^{-11}, t^{-7}, t^{-6}, t^{-4}, t^{-3}$
,
![]() $ t^{-2}$
, and
$ t^{-2}$
, and
![]() ${\mathcal O}_{X}^{\perp }$
is the
${\mathcal O}_{X}^{\perp }$
is the
![]() ${\mathbf {k}}$
-vector space with basis
${\mathbf {k}}$
-vector space with basis
![]() $u, u^2, u^3, u^5, u^6, u^{10}$
.
$u, u^2, u^3, u^5, u^6, u^{10}$
.