Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T16:08:29.287Z Has data issue: false hasContentIssue false
  • English
  • Français

Exponential Laws for the Nachbin Ported Topology

Published online by Cambridge University Press:  20 November 2018

C. Boyd
C. Boyd*
Affiliation:
Department of Mathematics University College Dublin Belfield Dublin 4 Ireland
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that for 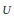$U$ and 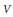$V$ balanced open subsets of 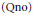$\left( \text{Qno} \right)$ Fréchet spaces 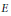$E$ and 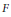$F$ that we have the topological identity

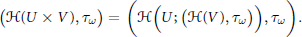$$\text{(}\mathcal{H}(U\times V),{{\tau }_{\omega }})=\left( \mathcal{H}\left( U;\left( \mathcal{H}(V),{{\tau }_{\omega }} \right) \right),{{\tau }_{\omega }} \right).$$

Analogous results for the compact open topology have long been established. We also give an example to show that the 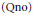$\left( \text{Qno} \right)$ hypothesis on both 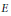$E$ and 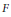$F$ is necessary.

Keywords

46G2018D1546M05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 43 , Issue 2 , 01 June 2000 , pp. 138 - 144
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Ansemil, J. M. and Ponte, S., Topologies associated with the compact open topology on H(U). Proc. Roy. Irish. Acad. Sect. A (1) 82(1982), 121–128.Google Scholar
[2] Aron, R. and Schottenloher, M., Compact holomorphic mappings on Banach spaces and the approximation property. Funct, J.. Anal. (1) 21(1976), 7–30.Google Scholar
[3] Bierstedt, K. D. and Meise, R., Nuclearity and the Schwartz property in the theory of holomorphic functions on metrizable locally convex spaces. In: Infinite Dimensional Holomorphy and Applications (ed. Matos, M.), North-Holland Math. Stud. 12(1977), 93–129.Google Scholar
[4] Bjon, S., On an exponential law for spaces of holomorphic functions. Math. Nachr. 131(1987), 201–204.Google Scholar
[5] Bjon, S. and Lindström, M., A general approach to infinite dimensional holomorphy. Monatsh. Math. 101(1986), 11–26.Google Scholar
[6] Bonet, J., Díaz, J. C. and Taskinen, J., Tensor stable Fréchet and DF-spaces. Collect. Math. (3) 42(1991), 199–236.Google Scholar
[7] Bonet, J., Dománski, P. and Mujica, J., Completeness of spaces of vector-valued holomorphic germs. Math. Scand. 75(1995), 250–260.Google Scholar
[8] Boyd, C., Distinguished preduals of the space of holomorphic functions. Rev. Mat. Univ. Complut. Madrid (2) 6(1993), 221–231.Google Scholar
[9] Boyd, C., Montel and reflexive preduals of the space of holomorphic functions. Studia Math. (3) 107(1993), 305–315.Google Scholar
[10] Boyd, C. and Peris, C., A projective description of the Nachbin ported topology. Math, J.. Anal. Appl. (3) 197(1996), 635–657.Google Scholar
[11] Brown, R., Function spaces and product topologies. Quart. Math, J.. Oxford (2) 15(1964), 238–250.Google Scholar
[12] Dineen, S., Complex analysis on locally convex spaces. North-Holland Math. Stud. 57, 1981.Google Scholar
[13] Dineen, S., Quasinormable spaces of holomorphic functions. Note Mat. (1) 13(1993), 155–195.Google Scholar
[14] Jarchow, H., Locally convex spaces. G, B.. Teubner, Stuttgart, 1981.Google Scholar
[15] Köthe, G., Topological Vector Spaces II. Springer-Verlag, Berlin-Heidelberg-New York, 1979.Google Scholar
[16] Mujica, J., A completeness criterion for inductive limits of Banach spaces. Functional Analysis, Holomorphy and Approximation Theory II (ed. I, G.. Zapata), North-Holland Math. Stud. 86(1984), 319–329.Google Scholar
[17] Mujica, J., A Banach-Dieudonné theorem for the space of germs of holomorphic functions. Funct, J.. Anal. 57(1984) 32–48.Google Scholar
[18] Mujica, J., Linearization of bounded holomorphic mappings on Banach spaces. Trans. Amer. Math. Soc. (2) 324(1991), 867–887.Google Scholar
[19] Mujica, J., Linearization of holomorphic mappings of bounded type. Progress in Functional Analysis (eds. K.-Bierstedt, D., Bonet, J., Horvath, J. and Maestre, M.),North-HollandMath. Stud. 130(1992), 149–162.Google Scholar
[20] Peris, A., Quasinormable spaces and the problem of Topologies of Grothendieck. Ann. Acad. Sci. Fenn. 19(1994), 167–203.Google Scholar
[21] Peris, A., Topological tensor product of a Fréchet Schwartz space and a Banach space. Studia Math. (2) 106(1993), 189–196.Google Scholar
[22] Schottenloher, M., ε-products and continuation of analytic mappings. Analyse Fonctionelle et Applications (ed. L. Nachbin), C. R. du Colloque d’Analyse, Instituto de Matematica, UFRJ, Rio de Janeiro, 1972. Herman Press, Paris, 1974, 261–270.Google Scholar