Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Pullman, N.
1964.
On the Number of Positive Entries in the Powers of a Non-Negative Matrix.
Canadian Mathematical Bulletin,
Vol. 7,
Issue. 4,
p.
525.
Heap, B. R.
and
Lynn, M. S.
1964.
The index of primitivity of a non-negative matrix.
Numerische Mathematik,
Vol. 6,
Issue. 1,
p.
120.
Mendelsohn, N. S.
1970.
A LINEAR DIOPHANTINE EQUATION WITH APPLICATIONS TO NON‐NEGATIVE MATRICES.
Annals of the New York Academy of Sciences,
Vol. 175,
Issue. 1,
p.
287.
Lewin, Mordechai
1971.
On exponents of primitive matrices.
Numerische Mathematik,
Vol. 18,
Issue. 2,
p.
154.
Cooper, Christopher D. H.
1973.
On the maximum eigenvalue of a reducible non-negative real matrix.
Mathematische Zeitschrift,
Vol. 131,
Issue. 3,
p.
213.
Coxson, Pamela G.
Larson, Loren C.
and
Schneider, Hans
1987.
Monomial patterns in the sequence Ab.
Linear Algebra and its Applications,
Vol. 94,
Issue. ,
p.
89.
Hartwig, Robert E.
and
Neumann, Michael
1993.
Bounds on the exponent of primitivity which depend on the spectrum and the minimal polynomial.
Linear Algebra and its Applications,
Vol. 184,
Issue. ,
p.
103.
Shen, Jian
1996.
An improvement of the Dulmage-Mendelsohn theorem.
Discrete Mathematics,
Vol. 158,
Issue. 1-3,
p.
295.
Akelbek, Mahmud
and
Kirkland, Steve
2009.
Coefficients of ergodicity and the scrambling index.
Linear Algebra and its Applications,
Vol. 430,
Issue. 4,
p.
1111.
Ananichev, Dmitry
Gusev, Vladimir
and
Volkov, Mikhail
2010.
Mathematical Foundations of Computer Science 2010.
Vol. 6281,
Issue. ,
p.
55.
Ananichev, D. S.
Volkov, M. V.
and
Gusev, V. V.
2013.
Primitive digraphs with large exponents and slowly synchronizing automata.
Journal of Mathematical Sciences,
Vol. 192,
Issue. 3,
p.
263.
Fomichev, V. M.
Avezova, Ya. E.
Koreneva, A. M.
and
Kyazhin, S. N.
2018.
Primitivity and Local Primitivity of Digraphs and Nonnegative Matrices.
Journal of Applied and Industrial Mathematics,
Vol. 12,
Issue. 3,
p.
453.
Nej, Monimala
and
Reddy, A. Satyanarayana
2019.
Exponents of primitive companion matrices.
Rocky Mountain Journal of Mathematics,
Vol. 49,
Issue. 5,
Fomichev, Vladimir
and
Koreneva, Alisa
2020.
Encryption performance and security of certain wide block ciphers.
Journal of Computer Virology and Hacking Techniques,
Vol. 16,
Issue. 3,
p.
197.
Fomichev, V. M.
2020.
Estimating Nonlinearity Characteristics for Iterative
Transformations of a Vector Space.
Journal of Applied and Industrial Mathematics,
Vol. 14,
Issue. 4,
p.
610.
Fomichev, V. M.
and
Avezova, Ya. E.
2020.
The Exact Formula for the Exponents of the Mixing Digraphs of Register Transformations.
Journal of Applied and Industrial Mathematics,
Vol. 14,
Issue. 2,
p.
308.
Fomichev, V. M.
2021.
On the Degree of Nonlinearity of the Coordinate Polynomials for a Product of Transformations of a Binary Vector Space.
Journal of Applied and Industrial Mathematics,
Vol. 15,
Issue. 2,
p.
212.
Fomichev, Vladimir
Bobrovskiy, Dmitry
Koreneva, Alisa
Nabiev, Timur
and
Zadorozhny, Dmitry
2022.
Data integrity algorithm based on additive generators and hash function.
Journal of Computer Virology and Hacking Techniques,
Vol. 18,
Issue. 1,
p.
31.
Lyu, Xiaoxu
Duan, Peihu
Duan, Zhisheng
and
Zhang, Zhao
2024.
Stability Analysis of Constrained Distributed Nonlinear and Linear Kalman Filters for Dynamical Systems With State Constraints.
IEEE Transactions on Aerospace and Electronic Systems,
Vol. 60,
Issue. 1,
p.
632.
Petersen, Karl
and
Salama, Ibrahim
2025.
Arrival of information at a target set in a network.
Monatshefte für Mathematik,
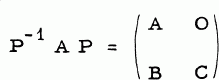
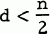 improves Wielandt's result.
improves Wielandt's result.