Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dobkin, David P.
Edelsbrunner, Herbert
and
Overmars, Mark H.
1990.
Searching for empty convex polygons.
Algorithmica,
Vol. 5,
Issue. 1-4,
p.
561.
Bárány, I.
Füredi, Z.
and
Lovász, L.
1990.
On the number of halving planes.
Combinatorica,
Vol. 10,
Issue. 2,
p.
175.
SCHMITT, Peter
1993.
Handbook of Convex Geometry.
p.
449.
Nešetřil, Jaroslav
and
Valtr, Pavel
1994.
A Ramsey-Type Theorem in the Plane.
Combinatorics, Probability and Computing,
Vol. 3,
Issue. 1,
p.
127.
Rote, G.
and
Tichy, R.F.
1996.
Quasi-Monte-Carlo methods and the dispersion of point sequences.
Mathematical and Computer Modelling,
Vol. 23,
Issue. 8-9,
p.
9.
Dey, Tamal K.
and
Shah, Nimish R.
1997.
On the number of simplicial complexes in Rd.
Computational Geometry,
Vol. 8,
Issue. 5,
p.
267.
Harborth, Heiko
1998.
Empty triangles in drawings of the complete graph.
Discrete Mathematics,
Vol. 191,
Issue. 1-3,
p.
109.
Tajima, Akira
1998.
Algorithms and Computation.
Vol. 1533,
Issue. ,
p.
378.
Dumitrescu, A.
2000.
Planar sets with few empty convex polygons.
Studia Scientiarum Mathematicarum Hungarica,
Vol. 36,
Issue. 1-2,
p.
93.
Morris, W.
and
Soltan, V.
2000.
The Erdos-Szekeres problem on points in convex position – a survey.
Bulletin of the American Mathematical Society,
Vol. 37,
Issue. 4,
p.
437.
Bárány, Imre
and
Károlyi, Gyula
2001.
Discrete and Computational Geometry.
Vol. 2098,
Issue. ,
p.
91.
Devillers, Olivier
Hurtado, Ferran
Károlyi, Gyula
and
Seara, Carlos
2003.
Chromatic variants of the Erdős–Szekeres theorem on points in convex position.
Computational Geometry,
Vol. 26,
Issue. 3,
p.
193.
Bárány, Imre
and
Valtr, Pável
2004.
Planar point sets with a small number of empty convex polygons.
Studia Scientiarum Mathematicarum Hungarica,
Vol. 41,
Issue. 2,
p.
243.
Pinchasi, Rom
Radoicic, Rados
and
Sharir, Micha
2004.
On empty convex polygons in a planar point set.
p.
391.
Pinchasi, Rom
Radoičić, Radoš
and
Sharir, Micha
2006.
On empty convex polygons in a planar point set.
Journal of Combinatorial Theory, Series A,
Vol. 113,
Issue. 3,
p.
385.
Aichholzer, Oswin
Fabila-Monroy, Ruy
Flores-Peñaloza, David
Hackl, Thomas
Huemer, Clemens
and
Urrutia, Jorge
2009.
Empty monochromatic triangles.
Computational Geometry,
Vol. 42,
Issue. 9,
p.
934.
Ahn, Hee-Kap
Bae, Sang Won
van Kreveld, Marc
Reinbacher, Iris
and
Speckmann, Bettina
2011.
Empty pseudo-triangles in point sets.
Discrete Applied Mathematics,
Vol. 159,
Issue. 18,
p.
2205.
García, Alfredo
2012.
Computational Geometry.
Vol. 7579,
Issue. ,
p.
249.
Fabila-Monroy, Ruy
and
Huemer, Clemens
2012.
Computational Geometry.
Vol. 7579,
Issue. ,
p.
220.
Balogh, József
González-Aguilar, Hernán
and
Salazar, Gelasio
2013.
Large convex holes in random point sets.
Computational Geometry,
Vol. 46,
Issue. 6,
p.
725.


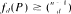 . Here a random construction
. Here a random construction 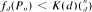 , where K(
, where K(