Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-24T14:01:34.640Z Has data issue: false hasContentIssue false
  • English
  • Français

Continuous Adjacency Preserving Maps on Real Matrices

Published online by Cambridge University Press:  20 November 2018

Leiba Rodman ,
Peter Šemrl  and
Ahmed R. Sourour
Leiba Rodman
Affiliation:
Department of Mathematics, College of William and Mary, P.O. Box 8795, Williamsburg, VA 23187-8795, U.S.A. e-mail: [email protected]
Peter Šemrl
Affiliation:
Department of Mathematics, University of Ljubljana, Jadranska 19, SI-1000 Ljubljana, Slovenia e-mail: [email protected]
Ahmed R. Sourour
Affiliation:
Department of Mathematics and Statistics, University of Victoria, Victoria, BC, V8W 3P4 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is proved that every adjacency preserving continuous map on the vector space of real matrices of fixed size, is either a bijective affine tranformation of the form 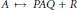$A\,\mapsto \,PAQ\,+\,R$, possibly followed by the transposition if the matrices are of square size, or its range is contained in a linear subspace consisting of matrices of rank at most one translated by some matrix $R$. The result extends previously known theorems where the map was assumed to be also injective.

Keywords

15A0315A04adjacency of matricescontinuous preserversaffine transformations
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 2 , 01 June 2005 , pp. 267 - 274
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Carter, D. S. and Vogt, A., Collinearity-preserving functions between Desarguesian planes. Mem. Amer. Math. Soc. 27(1980), 1–98.Google Scholar
[2] Fulton, W., Algebraic topology. A first course. Springer-Verlag, New York, 1995.Google Scholar
[3] Hua, L. K., Geometries of matrices I. Generalizations of von Staudt's theorem. Trans. Amer. Math. Soc. 57(1945), 441–481.Google Scholar
[4] Hua, L. K., Geometries of matrices I 1 . Arithmetical construction. Trans. Amer.Math. Soc. 57(1945), 482–490.Google Scholar
[5] Hua, L. K., Geometries of symmetric matrices over the real field, I. C. R. (Doklady) Acad. Sci. URSS 53(1946), 95–97.Google Scholar
[6] Hua, L. K., Geometries of symmetric matrices over the real field, II. C. R. (Doklady) Acad. Sci. URSS 53(1946), 195–196.Google Scholar
[7] Hua, L. K., Geometries of matrices, II. Study of involutions in the geometry of symmetric matrices. Trans. Amer. Math. Soc. 61(1947), 193–228.Google Scholar
[8] Hua, L. K., Geometries of matrices, III. Fundamental theorems in the geometries of symmetric matrices. Trans. Amer. Math. Soc. 61(1947), 229–255.Google Scholar
[9] Hua, L. K., Geometry of symmetric matrices over any field with characteristic other than two. Ann. of Math. 50(1949), 8–31.Google Scholar
[10] Hua, L. K., A theorem on matrices over a sfield and its applications. J. Chinese Math. Soc. 1(1951), 110–163.Google Scholar
[11] Lim, M. H., Rank and tensor rank preservers, Linear and Multilinear Algebra 33(1992), 7–21.Google Scholar
[12] Petek, T. and Šemrl, P., Adjacency preserving maps on matrices and operators. Proc. Roy. Soc. Edinburgh Sect. A. 132(2002), 661–684.Google Scholar
[13] Šemrl, P., On Hua's fundamental theorem of the geometry of rectangular matrices. J. Algebra 248(2002), 366–380.Google Scholar
[14] Šemrl, P., Hua's fundamental theorems of the geometry of matrices and related results. Linear Algebra Appl. 361(2003), 161–179.Google Scholar
[15] Wan, Z., Geometry of matrices. World Scientific, River Edge, NJ, 1996.Google Scholar