Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T01:35:17.083Z Has data issue: false hasContentIssue false
  • English
  • Français

Complete Families of Linearly Non-degenerate Rational Curves

Published online by Cambridge University Press:  20 November 2018

Matthew DeLand
Matthew DeLand*
Affiliation:
Department of Mathematics, Columbia University, New York, NY 10025, U.S.A. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that every complete family of linearly non-degenerate rational curves of degree 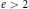$e\,>\,2$ in 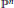${{\mathbb{P}}^{n}}$ has at most 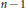$n\,-\,1$ moduli. For 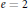$e\,=\,2$ we prove that such a family has at most $n$ moduli. The general method involves exhibiting a map from the base of a family 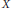$X$ to the Grassmannian of $e$-planes in 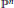${{\mathbb{P}}^{n}}$ and analyzing the resulting map on cohomology.

Keywords

14N0514H10
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 3 , 01 September 2011 , pp. 430 - 441
Copyright
Copyright © Canadian Mathematical Society 2011

References

[B] Białynicki-Birula, A., On homogeneous affine spaces of linear algebraic groups. Amer. J. Math. 85(1963), 577–582. doi:10.2307/2373109Google Scholar
[BG] Bloch, S. and Gieseker, D.. The positivity of the Chern classes of an ample vector bundle. Invent. Math. 12(1971), 112–117. doi:10.1007/BF01404655Google Scholar
[CHS] Coskun, I., Harris, J., and Starr, J., The effective cone of the Kontsevich moduli space. Canad. Math. Bull. 51(2008), no. 4, 519–534. doi:10.4153/CMB-2008-052-5Google Scholar
[CR] Chang, M. C. and Ran, Z., Dimension of families of space curves. CompositioMath. 90(1994), no. 1, 53–57.Google Scholar
[DEB] Debarre, O., Higher-dimensional algebraic geometry. Universitext, Springer-Verlag, New York, 2001.Google Scholar
[FP] Fulton, W. and Pandharipande, R., Notes on stable maps and quantum cohomology. In: Algebraic geometry—Santa Cruz 1995, Proc. Sympos. Pure Math., 62, Part 2, American Mathematical Society, Providence, RI, 1997, pp. 45–96.Google Scholar
[FUL] Fulton, W., Intersection theory. Second ed., Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics, 2, Springer-Verlag, Berlin, 1998.Google Scholar
[EGAII] Grothendieck, A., Eléments de géométrie algébrique. II. Étude globale élémentaire de quelques classes de morphismes. Inst. Hautes études Sci. Publ. Math. 8(1961).Google Scholar
[HAR] Hartshorne, R., Algebraic geometry. Graduate Texts in Mathematics, 52, Springer-Verlag, New York-Heidelberg, 1977.Google Scholar
[LG] Lakshamibai, V. and Gonciulea, N, Flag Varieties. Travaux en Cours, 63, Hermann, Paris, 2001.Google Scholar