Published online by Cambridge University Press: 20 November 2018
Let n and k be integers with n ≥ k ≥ 3. Denote by f(n, k) the largest positive integer for which there exists a set S of f (n, k) integers satisfying (i) 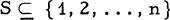 and (ii) no k members of S have pairwise the same greatest common divisor. The problem of determining f(n, k) appears to be difficult. Erdős [2[ proved that there is an absolute constant c > 1 such that for every ∈ > 0 and every fixed k
and (ii) no k members of S have pairwise the same greatest common divisor. The problem of determining f(n, k) appears to be difficult. Erdős [2[ proved that there is an absolute constant c > 1 such that for every ∈ > 0 and every fixed k
1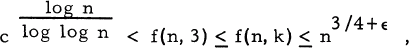
provided n > no (k, ∈). In [l[ it i s proved that for every ∈ > 0 and every fixed k