Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T03:58:05.269Z Has data issue: false hasContentIssue false
  • English
  • Français

An Almost Krull Domain with Divisorial Height One Primes

Published online by Cambridge University Press:  20 November 2018

J. T. Arnold  and
Ryuki Matsuda
J. T. Arnold
Affiliation:
Virginia Polytechnic Institute and State University, Blacksburg, Virginia24061
Ryuki Matsuda
Affiliation:
Ibaraki University, Mito, Ibaraki 310, Japan
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

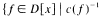E. Pirtle has conjectured that if D is an almost Krull domain in which the height one prime ideals are divisorial then D is a Krull domain. An example is given to show that this is not the case. Further, let U = and let 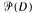denote the set of prime ideals of D which are minimal over some ideal (a):(b), where a, b ∈ D. If Dp is a valuation ring for each let 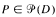then Huckaba and Papick have asked whether D[x]U must be a Prufer domain. The given example shows that it need not be.

Keywords

13G0513F99
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 29 , Issue 1 , 01 March 1986 , pp. 50 - 53
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Arnold, J. and Brewer, J., Kronecker function rings and flat D[x]-modules, Proc. Amer. Math. Soc. 27 (1971), pp. 483–485.Google Scholar
2. Eakin, P. and Silver, J., Rings which are almost polynomial rings, Trans. Amer. Math. Soc. 174 (1972), pp. 425–449.Google Scholar
3. Gilmer, R., Overrings of Priifer domains, J. Algebra, 4 (1966), pp. 331–340.Google Scholar
4. Gilmer, R., An embedding theorem for HCF rings, Proc. Camb. Phil. Soc. 68 (1970), pp. 583–587.Google Scholar
5. Gilmer, R., Multiplicative Ideal Theory, Marcel Dekker, New York, 1972.Google Scholar
6. Griffin, M., Some results on v-multiplication rings, Can. J. Math. 19 (1967), pp. 710–722.Google Scholar
7. Heinzer, W. and Ohm, J., An essential ring which is not a v-multiplication ring, Can. J. Math. 25 (1973), pp. 856–861.Google Scholar
8. Huckaba, J. and Papick, I., A localization ofR[x], Can. J. Math. 33 (1981), pp. 103–115.Google Scholar
9. Hutchins, H., Examples of Commutative Rings, Polygonal Publishing House, New Jersey, 1981.Google Scholar
10. Matsuda, R., On a question posed by Huckaba-Papick, Proc. Japan Acad., Ser. A, 59 (1983), pp. 21–23.Google Scholar
11. Matsuda, R., On a question posed by Huckaba-Papick II, Proc. Japan Acad., Ser. A, 59 (1983), pp. 379–381.Google Scholar
12. Pirtle, E., Integral domains which are almost Krull, J. Sci. Hiroshima Univ., Ser. A-I, 32 (1968), pp. 441–447.Google Scholar
13. Pirtle, E., Families of valuations and semigroups of fractionary ideal classes, Trans. Amer. Math. Soc. 144 (1969), pp. 427–439.Google Scholar
14. Pirtle, E., On a generalization of Krull domains, J. Algebra, 14 (1970), pp. 485–492.Google Scholar
15. Pirtle, E., A note on almost Dedekind domains, Publ. Math. Debrecen, 17 (1970), pp. 243—247.Google Scholar