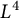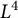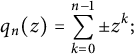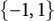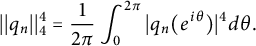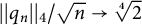1 Introduction
The study of Littlewood polynomials enjoys a long and outstanding history [Reference Montgomery22]. A polynomial with all coefficients in
![]() $\{-1,1\}$
is called a Littlewood polynomial, and we denote by
$\{-1,1\}$
is called a Littlewood polynomial, and we denote by
![]() $\mathcal {L}_n$
the family of Littlewood polynomials of degree
$\mathcal {L}_n$
the family of Littlewood polynomials of degree
![]() $n-1$
; that is,
$n-1$
; that is,
 $$ \begin{align*} \mathcal{L}_n :=\left\{q_n: q_n(z)=\sum_{k=0}^{n-1}\varepsilon_k z^{k},\quad\varepsilon_k\in\{-1,1\}\right\}. \end{align*} $$
$$ \begin{align*} \mathcal{L}_n :=\left\{q_n: q_n(z)=\sum_{k=0}^{n-1}\varepsilon_k z^{k},\quad\varepsilon_k\in\{-1,1\}\right\}. \end{align*} $$
The
![]() $L^p$
norm of Littlewood polynomials on the unit circle has been a fascinating and classical subject of many studies over the last 60 years [Reference Borwein and Lockhart7, Reference Borwein and Mossinghoff8, Reference Erdős10, Reference Erdős11, Reference Littlewood20, Reference Littlewood21, Reference Newman23, Reference Newman and Byrnes24]. Here, the
$L^p$
norm of Littlewood polynomials on the unit circle has been a fascinating and classical subject of many studies over the last 60 years [Reference Borwein and Lockhart7, Reference Borwein and Mossinghoff8, Reference Erdős10, Reference Erdős11, Reference Littlewood20, Reference Littlewood21, Reference Newman23, Reference Newman and Byrnes24]. Here, the
![]() $L^p$
norm
$L^p$
norm
![]() $(1\leq p<\infty )$
of
$(1\leq p<\infty )$
of
![]() $q_n\in \mathcal {L}_n$
on the unit circle is given by
$q_n\in \mathcal {L}_n$
on the unit circle is given by
 $$ \begin{align*}||q_n||_p:=\left(\frac{1}{2\pi}\int_0^{2\pi}|q_n(e^{i\theta})|^p d\theta\right)^{\frac{1}{p}},\end{align*} $$
$$ \begin{align*}||q_n||_p:=\left(\frac{1}{2\pi}\int_0^{2\pi}|q_n(e^{i\theta})|^p d\theta\right)^{\frac{1}{p}},\end{align*} $$
while
![]() $||q_n||_{\infty }$
is the supremum of
$||q_n||_{\infty }$
is the supremum of
![]() $|q_n(z)|$
on the unit circle. The
$|q_n(z)|$
on the unit circle. The
![]() $L^1, L^4$
, and
$L^1, L^4$
, and
![]() $L^{\infty }$
norms hold special significance in the field of analysis.
$L^{\infty }$
norms hold special significance in the field of analysis.
Littlewood [Reference Littlewood20, Section 6] asked how slowly the
![]() $L^4$
norm of
$L^4$
norm of
![]() $q_n\in \mathcal {L}_n$
can grow with n. Subsequently, the
$q_n\in \mathcal {L}_n$
can grow with n. Subsequently, the
![]() $L^4$
norm has been studied extensively, which is of interests in communication theory [Reference Borwein5, Reference Borwein, Choi and Jedwab6, Reference Golay12, Reference Høholdt and Jensen14, Reference Jedwab, Helleseth, Sarwate, Song and Yang15, Reference Jensen, Jensen and Høholdt17]. There are two natural measures which are often used in the investigation of how small the
$L^4$
norm has been studied extensively, which is of interests in communication theory [Reference Borwein5, Reference Borwein, Choi and Jedwab6, Reference Golay12, Reference Høholdt and Jensen14, Reference Jedwab, Helleseth, Sarwate, Song and Yang15, Reference Jensen, Jensen and Høholdt17]. There are two natural measures which are often used in the investigation of how small the
![]() $L^4$
norm can be. The first one is the ratio
$L^4$
norm can be. The first one is the ratio
![]() $||q_n||_4/||q_n||_2$
; that is,
$||q_n||_4/||q_n||_2$
; that is,
![]() $||q_n||_4/\sqrt {n}$
. The other is the merit factor
$||q_n||_4/\sqrt {n}$
. The other is the merit factor
 $$ \begin{align} \text{MF}(q_n):=\frac{||q_n||_2^4}{||q_n||_4^4-||q_n||_2^4}=\frac{n^2}{||q_n||_4^4-n^2}, \end{align} $$
$$ \begin{align} \text{MF}(q_n):=\frac{||q_n||_2^4}{||q_n||_4^4-||q_n||_2^4}=\frac{n^2}{||q_n||_4^4-n^2}, \end{align} $$
which is considered in the context of the theory of communications [Reference Beenker, Claasen and Hermens3], where Littlewood polynomials with large merit factor correspond to signals with uniformly distributed energy over frequency. Obviously, a small
![]() $L^4$
norm corresponds to a large merit factor. Moreover, establishing the minimum achievable
$L^4$
norm corresponds to a large merit factor. Moreover, establishing the minimum achievable
![]() $L^4$
norm for Littlewood polynomials has demonstrated substantial importance in theoretical physics [Reference Bernasconi4], where Littlewood polynomials with the largest merit factor correspond to the ground states of Bernasconi’s Ising spin model.
$L^4$
norm for Littlewood polynomials has demonstrated substantial importance in theoretical physics [Reference Bernasconi4], where Littlewood polynomials with the largest merit factor correspond to the ground states of Bernasconi’s Ising spin model.
Littlewood’s question has sparked much interest among mathematicians and physicists (see [Reference Jedwab, Helleseth, Sarwate, Song and Yang15] for a survey of relevant results and historical developments). In 1968, Littlewood [Reference Littlewood21] constructed a sequence of polynomials, of Rudin–Shapiro type, with asymptotic merit factor
![]() $3$
; that is, the ratio
$3$
; that is, the ratio
![]() $||q_n||_4/\sqrt {n}$
is asymptotically
$||q_n||_4/\sqrt {n}$
is asymptotically
![]() $\sqrt [4]{4/3}$
. In 1988, Hødoldt and Jensen [Reference Høholdt and Jensen14], working in information theory, showed that this ratio for a sequence of Littlewood polynomials derived from Fekete polynomials is asymptotically
$\sqrt [4]{4/3}$
. In 1988, Hødoldt and Jensen [Reference Høholdt and Jensen14], working in information theory, showed that this ratio for a sequence of Littlewood polynomials derived from Fekete polynomials is asymptotically
![]() $\sqrt [4]{7/6}$
, correspondingly, with the asymptotic merit factor
$\sqrt [4]{7/6}$
, correspondingly, with the asymptotic merit factor
![]() $6$
. They conjectured that the asymptotic value of this ratio cannot be further reduced, and in fact,
$6$
. They conjectured that the asymptotic value of this ratio cannot be further reduced, and in fact,
![]() $\sqrt [4]{7/6}$
has remained the smallest published asymptotic value for more than two decades. In 2013, Jedwab, Katz, and Schmidt [Reference Jedwab, Katz and Schmidt16] made a major discovery indicating that this is not the minimum asymptotic value, thus disproving the abovementioned conjecture. They proved that there exists a sequence of Littlewood polynomials, derived from Fekete polynomials, with the limit of the ratio less than
$\sqrt [4]{7/6}$
has remained the smallest published asymptotic value for more than two decades. In 2013, Jedwab, Katz, and Schmidt [Reference Jedwab, Katz and Schmidt16] made a major discovery indicating that this is not the minimum asymptotic value, thus disproving the abovementioned conjecture. They proved that there exists a sequence of Littlewood polynomials, derived from Fekete polynomials, with the limit of the ratio less than
![]() $\sqrt [4]{22/19}$
.
$\sqrt [4]{22/19}$
.
The roots of all these explorations actually go back to the original Littlewood’s conjecture [Reference Littlewood20] from 1966 which states that, for all
![]() $n\geq 1$
, there exists a polynomial
$n\geq 1$
, there exists a polynomial
![]() $q_n\in \mathcal {L}_n$
such that
$q_n\in \mathcal {L}_n$
such that
for all complex z of modulus 1, where
![]() $C_1$
and
$C_1$
and
![]() $C_2$
are positive absolute constants. Polynomials satisfying (2) are known as flat polynomials. This conjecture was discussed in detail in his well-known 1968 monograph [Reference Littlewood21, Problem 19], in which he laid out his
$C_2$
are positive absolute constants. Polynomials satisfying (2) are known as flat polynomials. This conjecture was discussed in detail in his well-known 1968 monograph [Reference Littlewood21, Problem 19], in which he laid out his
![]() $30$
favorite problems. A significant result by Kahane [Reference Kahane18, Reference Kahane19] establishes that there exist ultra-flat polynomials with coefficients of modulus 1, namely, polynomials that satisfy
$30$
favorite problems. A significant result by Kahane [Reference Kahane18, Reference Kahane19] establishes that there exist ultra-flat polynomials with coefficients of modulus 1, namely, polynomials that satisfy
for all z with
![]() $|z|=1$
. Subsequently, an interesting result, due to Beck [Reference Beck2], states that flat polynomials exist with coefficients being 400th roots of unity. However, for the more restrictive class of Littlewood polynomials, much less progress has been made over the next few decades until 2020. Then Littlewood’s conjecture was famously confirmed by Balister, Bollobás, Morris, Sahasrabudhe, and Tiba [Reference Balister, Bollobás, Morris, Sahasrabudhe and Tiba1], who showed that flat Littlewood polynomials exist and answered the question of Erdős [Reference Erdős10, Problem 26].
$|z|=1$
. Subsequently, an interesting result, due to Beck [Reference Beck2], states that flat polynomials exist with coefficients being 400th roots of unity. However, for the more restrictive class of Littlewood polynomials, much less progress has been made over the next few decades until 2020. Then Littlewood’s conjecture was famously confirmed by Balister, Bollobás, Morris, Sahasrabudhe, and Tiba [Reference Balister, Bollobás, Morris, Sahasrabudhe and Tiba1], who showed that flat Littlewood polynomials exist and answered the question of Erdős [Reference Erdős10, Problem 26].
Newman and Byrnes [Reference Newman and Byrnes24] calculated the expected
![]() $L^4$
norm of
$L^4$
norm of
![]() $q_n\in \mathcal {L}_n$
, specifically,
$q_n\in \mathcal {L}_n$
, specifically,
and therefore the expected merit factor is 1. Borwein and Lockhart [Reference Borwein and Lockhart7] showed that the ratio
![]() $||q_n||_4/\sqrt {n}$
converges to
$||q_n||_4/\sqrt {n}$
converges to
![]() $\sqrt [4]{2}$
in probability for
$\sqrt [4]{2}$
in probability for
![]() $q_n\in \mathcal {L}_n$
, equivalently, MF
$q_n\in \mathcal {L}_n$
, equivalently, MF
![]() $(q_n)\rightarrow 1$
in probability. In [Reference Borwein and Mossinghoff8], Borwein and Mossinghoff explicitly calculated the
$(q_n)\rightarrow 1$
in probability. In [Reference Borwein and Mossinghoff8], Borwein and Mossinghoff explicitly calculated the
![]() $L^4$
norm of Rudin–Shapiro-like polynomials. In [Reference Salem and Zygmund26], Salem and Zygmund showed that the supremum of Littlewood polynomials on the unit disk lies between
$L^4$
norm of Rudin–Shapiro-like polynomials. In [Reference Salem and Zygmund26], Salem and Zygmund showed that the supremum of Littlewood polynomials on the unit disk lies between
![]() $c_1\sqrt {n\log {n}}$
and
$c_1\sqrt {n\log {n}}$
and
![]() $c_2\sqrt {n\log {n}}$
. Indeed, Halász [Reference Halász13] proved that
$c_2\sqrt {n\log {n}}$
. Indeed, Halász [Reference Halász13] proved that
![]() $\lim ||q_n/\sqrt {n\log {n}}||_{\infty }=1$
almost surely.
$\lim ||q_n/\sqrt {n\log {n}}||_{\infty }=1$
almost surely.
The aim of this paper is to prove the almost sure convergence of
![]() $L^4$
norm of Littlewood polynomials. Our main result is the following.
$L^4$
norm of Littlewood polynomials. Our main result is the following.
Theorem 1 Let
![]() $q_n\in \mathcal {L}_n$
. Then
$q_n\in \mathcal {L}_n$
. Then
 $$ \begin{align*} \frac{||q_n||_4}{\sqrt{n}}\rightarrow \sqrt[4]{2} \end{align*} $$
$$ \begin{align*} \frac{||q_n||_4}{\sqrt{n}}\rightarrow \sqrt[4]{2} \end{align*} $$
almost surely.
This result has been conjectured by Borwein and Lockhart and numerical simulations were performed by Robinson in her master’s thesis [Reference Robinson25], confirming the rationality of this conjecture and consistent with our theoretical result. An extension of Theorem 1 to a more general case is included in Section 4, where only a fourth moment condition is assumed.
2 Preliminary results
In this section, we present several lemmas before we prove Theorem 1. We let
![]() ${A_n^m=n!/(n-m)!}$
and the combinatorial number of selecting m elements from n distinct elements is denoted by
${A_n^m=n!/(n-m)!}$
and the combinatorial number of selecting m elements from n distinct elements is denoted by
![]() $\binom {n}{m} = n!/ (n-m)!m!$
. To ensure convenience in calculations, we will adjust the indices from “
$\binom {n}{m} = n!/ (n-m)!m!$
. To ensure convenience in calculations, we will adjust the indices from “
![]() $0$
to
$0$
to
![]() $n-1$
” to “
$n-1$
” to “
![]() $1$
to n” at a few places, given that the
$1$
to n” at a few places, given that the
![]() $L^4$
norms of
$L^4$
norms of
![]() $\sum _{k=0}^{n-1}\varepsilon _k z^{k}$
and
$\sum _{k=0}^{n-1}\varepsilon _k z^{k}$
and
![]() $\sum _{k=1}^{n}\varepsilon _k z^{k}$
on the unit circle are the same.
$\sum _{k=1}^{n}\varepsilon _k z^{k}$
on the unit circle are the same.
Lemma 2 Let
![]() $q_n\in \mathcal {L}_n$
. The following assertions hold:
$q_n\in \mathcal {L}_n$
. The following assertions hold:
-
(i) If n is even, then
 $$ \begin{align*}\mathbb{E}(||q_n||_4^8 )=4n^4+\frac{4}{3}n^3-19n^2+\frac{56}{3}n.\end{align*} $$
$$ \begin{align*}\mathbb{E}(||q_n||_4^8 )=4n^4+\frac{4}{3}n^3-19n^2+\frac{56}{3}n.\end{align*} $$
-
(ii) If n is odd, then
 $$ \begin{align*}\mathbb{E}(||q_n||_4^8 )=4n^4+\frac{4}{3}n^3-19n^2+\frac{56}{3}n-4.\end{align*} $$
$$ \begin{align*}\mathbb{E}(||q_n||_4^8 )=4n^4+\frac{4}{3}n^3-19n^2+\frac{56}{3}n-4.\end{align*} $$
-
(iii) If n is even, then
 $$ \begin{align*}\mathbb{E}(||q_{n+1}||_4^4 \cdot ||q_n||_4^4 )=4n^4+\frac{28}{3}n^3-21n^2+\frac{53}{3}n.\end{align*} $$
$$ \begin{align*}\mathbb{E}(||q_{n+1}||_4^4 \cdot ||q_n||_4^4 )=4n^4+\frac{28}{3}n^3-21n^2+\frac{53}{3}n.\end{align*} $$
-
(iv) If n is odd, then
 $$ \begin{align*}\mathbb{E}(||q_{n+1}||_4^4 \cdot ||q_n||_4^4)=4n^4+\frac{28}{3}n^3-21n^2+\frac{53}{3}n-4.\end{align*} $$
$$ \begin{align*}\mathbb{E}(||q_{n+1}||_4^4 \cdot ||q_n||_4^4)=4n^4+\frac{28}{3}n^3-21n^2+\frac{53}{3}n-4.\end{align*} $$
In particular, the values in (i)–(iv) are positive integers.
Proof By observation,
 $$ \begin{align} ||q_n||_4^4 =\sum\limits_{j+k=l+m\atop 1\leq j,k,l,m\leq n}\varepsilon_j\varepsilon_k\varepsilon_l\varepsilon_m. \end{align} $$
$$ \begin{align} ||q_n||_4^4 =\sum\limits_{j+k=l+m\atop 1\leq j,k,l,m\leq n}\varepsilon_j\varepsilon_k\varepsilon_l\varepsilon_m. \end{align} $$
Therefore, we obtain
 $$ \begin{align} \mathbb{E}\big(||q_n||_4^8) =\mathbb{E}\left(\sum_{\tiny \begin{array}{c} j+k=l+m\\ j' +k' =l'+m'\\ 1\leq j,k,l,m,j',k',l',m'\leq n\end{array}}\varepsilon_j\varepsilon_k\varepsilon_l\varepsilon_m\varepsilon_{j'} \varepsilon_{k'} \varepsilon_{l'} \varepsilon_{m'}\right), \end{align} $$
$$ \begin{align} \mathbb{E}\big(||q_n||_4^8) =\mathbb{E}\left(\sum_{\tiny \begin{array}{c} j+k=l+m\\ j' +k' =l'+m'\\ 1\leq j,k,l,m,j',k',l',m'\leq n\end{array}}\varepsilon_j\varepsilon_k\varepsilon_l\varepsilon_m\varepsilon_{j'} \varepsilon_{k'} \varepsilon_{l'} \varepsilon_{m'}\right), \end{align} $$
and
 $$ \begin{align} \mathbb{E}(||q_{n+1}||_4^4 \cdot ||q_n||_4^4)=\mathbb{E}\left(\sum_{\tiny \begin{array}{c} j+k=l+m\\ j' +k' =l'+m'\\ 1\leq j,k,l,m\leq n+1\\1\leq j',k',l',m'\leq n \end{array}}\varepsilon_j\varepsilon_k\varepsilon_l\varepsilon_m\varepsilon_{j'} \varepsilon_{k'} \varepsilon_{l'} \varepsilon_{m'}\right). \end{align} $$
$$ \begin{align} \mathbb{E}(||q_{n+1}||_4^4 \cdot ||q_n||_4^4)=\mathbb{E}\left(\sum_{\tiny \begin{array}{c} j+k=l+m\\ j' +k' =l'+m'\\ 1\leq j,k,l,m\leq n+1\\1\leq j',k',l',m'\leq n \end{array}}\varepsilon_j\varepsilon_k\varepsilon_l\varepsilon_m\varepsilon_{j'} \varepsilon_{k'} \varepsilon_{l'} \varepsilon_{m'}\right). \end{align} $$
Our goal is to count the number of terms with nonvanishing expectation, namely, we concern the terms such that
![]() $\mathbb {E}\big (\varepsilon _j\varepsilon _k\varepsilon _l\varepsilon _m\varepsilon _{j'} \varepsilon _{k'} \varepsilon _{l'} \varepsilon _{m'}\big )=1$
.
$\mathbb {E}\big (\varepsilon _j\varepsilon _k\varepsilon _l\varepsilon _m\varepsilon _{j'} \varepsilon _{k'} \varepsilon _{l'} \varepsilon _{m'}\big )=1$
.
For (i), as shown in Figure 1, we divide the eight parameters into two groups. The proof proceeds by considering three cases according to the choice of the subscripts
![]() $j,k,l,m,j' , k', l', m'$
.
$j,k,l,m,j' , k', l', m'$
.

Figure 1 Grouping of parameters for (i) and (ii).
Case 1 Each group has two equal pairs of subscripts.
We take the Group A as an example. There are three options for subscripts
![]() $j,k,l,m$
:
$j,k,l,m$
:
The three types above correspond to
respectively. A similar approach works for Group B. Thus, there are nine different subcases in Case 1 (see Table 1 for the quantity corresponding to each subcase).
Table 1 Subcases of Case 1 for (i) and (ii).

Consequently, the sum of these quantities is
![]() $4n^4-4n^3+n^2$
. Incidentally, Case 1 is the most numerous.
$4n^4-4n^3+n^2$
. Incidentally, Case 1 is the most numerous.
Case 2 Each group has only one pair of equal subscripts.
Since we are concerned with the terms such that
![]() $\mathbb {E}\big (\varepsilon _j\varepsilon _k\varepsilon _l\varepsilon _m\varepsilon _{j'} \varepsilon _{k'} \varepsilon _{l'} \varepsilon _{m'}\big )=1$
, if one of the Groups A and B has only one pair of equal subscripts, then so does the other group.
$\mathbb {E}\big (\varepsilon _j\varepsilon _k\varepsilon _l\varepsilon _m\varepsilon _{j'} \varepsilon _{k'} \varepsilon _{l'} \varepsilon _{m'}\big )=1$
, if one of the Groups A and B has only one pair of equal subscripts, then so does the other group.
Let us take the subcase
![]() $j\neq k,~l=m$
in Group A as an example. Under this assumption, it is worth noting that both j and k are either odd or even. Hence, if j and k have been determined, then there must be
$j\neq k,~l=m$
in Group A as an example. Under this assumption, it is worth noting that both j and k are either odd or even. Hence, if j and k have been determined, then there must be
![]() $l=m=\frac {j+k}{2}$
. Now, correspondingly, Group B has the following options:
$l=m=\frac {j+k}{2}$
. Now, correspondingly, Group B has the following options:
Bearing in mind that n is even, whether j and k are both odd or even, the corresponding quantity is
![]() $A_{\frac {n}{2}}^2\cdot 4=n^2-2n$
. Hence, for such a subcase, the quantity of options is
$A_{\frac {n}{2}}^2\cdot 4=n^2-2n$
. Hence, for such a subcase, the quantity of options is
![]() $2n^2-4n$
. Similarly, in the subcase
$2n^2-4n$
. Similarly, in the subcase
![]() $j=k,~l\neq m$
, the quantity is also
$j=k,~l\neq m$
, the quantity is also
![]() $2n^2-4n$
. Consequently, the quantity of options in Case 2 is
$2n^2-4n$
. Consequently, the quantity of options in Case 2 is
![]() $4n^2-8n$
.
$4n^2-8n$
.
Case 3 Each group has no pair of equal subscripts.
In this case, we suppose that
![]() $j\neq k\neq l \neq m$
for Group A. Recall that
$j\neq k\neq l \neq m$
for Group A. Recall that
![]() $j+k=l+m,~1\leq j,k,l,m\leq n$
. Let us take
$j+k=l+m,~1\leq j,k,l,m\leq n$
. Let us take
![]() $\varepsilon _1\varepsilon _5\varepsilon _2\varepsilon _4$
as a simple example. Since we want
$\varepsilon _1\varepsilon _5\varepsilon _2\varepsilon _4$
as a simple example. Since we want
![]() $\mathbb {E}\big (\varepsilon _j\varepsilon _k\varepsilon _l\varepsilon _m\varepsilon _{j'} \varepsilon _{k'} \varepsilon _{l'} \varepsilon _{m'}\big )=1$
, if
$\mathbb {E}\big (\varepsilon _j\varepsilon _k\varepsilon _l\varepsilon _m\varepsilon _{j'} \varepsilon _{k'} \varepsilon _{l'} \varepsilon _{m'}\big )=1$
, if
![]() $\varepsilon _1\varepsilon _5\varepsilon _2\varepsilon _4$
appears in Group A, then, correspondingly, one of the following must appear in Group B:
$\varepsilon _1\varepsilon _5\varepsilon _2\varepsilon _4$
appears in Group A, then, correspondingly, one of the following must appear in Group B:
Therefore, it suffices to consider Group A, and for every choice in Group A, there are eight choices in Group B correspondingly.
Now the problem naturally transforms into considering how many options there are for
![]() $j,k,l,m$
to satisfy the following conditions:
$j,k,l,m$
to satisfy the following conditions:
For example, we observe that this set of subscripts
![]() $\{1,2,4,5\}$
will appear eight times in Group A by adjusting the order reasonably, as shown in (9). For brevity, we first consider the non-repeating case, regardless of the order. For any even number n, the quantity of options in non-repeating case is
$\{1,2,4,5\}$
will appear eight times in Group A by adjusting the order reasonably, as shown in (9). For brevity, we first consider the non-repeating case, regardless of the order. For any even number n, the quantity of options in non-repeating case is
As was mentioned earlier, each set of subscripts has eight different kinds of ordering. Therefore, the quantity of options for Group A is
![]() $\frac {2}{3}n^3-3n^2+\frac {10}{3}n$
. Combined with the previous analysis for Group B, we obtain that the quantity of options in Case 3 is
$\frac {2}{3}n^3-3n^2+\frac {10}{3}n$
. Combined with the previous analysis for Group B, we obtain that the quantity of options in Case 3 is
![]() $\frac {16}{3}n^3-24n^2+\frac {80}{3}n$
. Summing the quantities in all cases, we obtain (i), as desired.
$\frac {16}{3}n^3-24n^2+\frac {80}{3}n$
. Summing the quantities in all cases, we obtain (i), as desired.
A reasoning similar to the proof of (i) leads to (ii). For reader’s convenience, we outline the proof. For Case 1, it is exactly the same as before, since it makes no difference whether n is odd or even. For Case 2, there are two subcases for Group A,
![]() $j\neq k,~l=m$
and
$j\neq k,~l=m$
and
![]() $j=k,~l\neq m$
. Take the subcase
$j=k,~l\neq m$
. Take the subcase
![]() $j\neq k,~l=m$
as an example. Bearing in mind that n is odd,
$j\neq k,~l=m$
as an example. Bearing in mind that n is odd,
-
• if j and k are both odd, then the corresponding quantity is
 $A_{\frac {n+1}{2}}^2\cdot 4$
,
$A_{\frac {n+1}{2}}^2\cdot 4$
, -
• if j and k are both even, then the corresponding quantity is
 $A_{\frac {n-1}{2}}^2\cdot 4$
.
$A_{\frac {n-1}{2}}^2\cdot 4$
.
Hence, the quantity of options for such a subcase is
![]() $2n^2-4n+2$
. For the other subcase, the argument is the same as above. Consequently, the quantity of options in Case 2 is
$2n^2-4n+2$
. For the other subcase, the argument is the same as above. Consequently, the quantity of options in Case 2 is
![]() $4n^2-8n+4$
. For Case 3, as discussed in (i), it suffices to solve the following problem: how many options there are for
$4n^2-8n+4$
. For Case 3, as discussed in (i), it suffices to solve the following problem: how many options there are for
![]() $j,k,l,m$
to satisfy the following conditions:
$j,k,l,m$
to satisfy the following conditions:
where n is odd. Similarly, we still consider the non-repeating case first. For any odd number n, the quantity of options in non-repeating case is
 $$ \begin{align*}4\binom{2}{2}+4\binom{3}{2}+4\binom{4}{2} +\cdots+4\binom{\frac{n-1}{2}-1}{2}+3\binom{\frac{n-1}{2}}{2}=\frac{1}{12}n^3-\frac{3}{8}n^2+\frac{5}{12}n-\frac{1}{8}.\end{align*} $$
$$ \begin{align*}4\binom{2}{2}+4\binom{3}{2}+4\binom{4}{2} +\cdots+4\binom{\frac{n-1}{2}-1}{2}+3\binom{\frac{n-1}{2}}{2}=\frac{1}{12}n^3-\frac{3}{8}n^2+\frac{5}{12}n-\frac{1}{8}.\end{align*} $$
Therefore, the quantity of options for Group A is
![]() $\frac {2}{3}n^3-3n^2+\frac {10}{3}n-1$
. Further, with consideration of Group B, there are
$\frac {2}{3}n^3-3n^2+\frac {10}{3}n-1$
. Further, with consideration of Group B, there are
![]() $\frac {16}{3}n^3-24n^2+\frac {80}{3}n-8$
options in Case 3. Consequently, combing three cases, we get the assertion in (ii).
$\frac {16}{3}n^3-24n^2+\frac {80}{3}n-8$
options in Case 3. Consequently, combing three cases, we get the assertion in (ii).
For (iii) and (iv), we divide the eight parameters into two groups as shown in Figure 2 and the proof proceeds by considering three cases as in (i).

Figure 2 Grouping of parameters for (iii) and (iv).
We prove (iii) first. Case 1 has the following nine subcases and the corresponding quantity of options for each subcase is shown in Table 2. Therefore, the sum of these quantities in Case 1 is
![]() $4n^4+4n^3-n^2-n$
. For Cases 2 and 3, if we want
$4n^4+4n^3-n^2-n$
. For Cases 2 and 3, if we want
![]() $\mathbb {E}\big (\varepsilon _j\varepsilon _k\varepsilon _l\varepsilon _m\varepsilon _{j'} \varepsilon _{k'} \varepsilon _{l'} \varepsilon _{m'}\big )=1$
, then it suffices to consider
$\mathbb {E}\big (\varepsilon _j\varepsilon _k\varepsilon _l\varepsilon _m\varepsilon _{j'} \varepsilon _{k'} \varepsilon _{l'} \varepsilon _{m'}\big )=1$
, then it suffices to consider
![]() $1\leq j,k,l,m\leq n$
. Therefore, the problems transform to the same one as in (i). Consequently, the quantity of options in Cases 2 and 3 is
$1\leq j,k,l,m\leq n$
. Therefore, the problems transform to the same one as in (i). Consequently, the quantity of options in Cases 2 and 3 is
![]() $4n^2-8n$
and
$4n^2-8n$
and
![]() $\frac {16}{3}n^3-24n^2+\frac {80}{3}n$
, respectively. Hence, we complete the proof of (iii).
$\frac {16}{3}n^3-24n^2+\frac {80}{3}n$
, respectively. Hence, we complete the proof of (iii).
Table 2 Subcases of Case 1 for (iii) and (iv).

Finally, we prove (iv). The proof is divided into three cases as before. Case 1 is the same as in (iii) since it makes no difference whether n is odd or even. For Cases 2 and 3, in fact, it suffices to consider
![]() $1\leq j,k,l,m\leq n$
and thus follow the same arguments in (ii). Hence, we obtain (iv) and complete the proof of Lemma 2.
$1\leq j,k,l,m\leq n$
and thus follow the same arguments in (ii). Hence, we obtain (iv) and complete the proof of Lemma 2.
Notations Let
![]() $T_0=0$
. For any positive integer
$T_0=0$
. For any positive integer
![]() $n\geq 1$
, define
$n\geq 1$
, define
and
It is worth noting that
 $$ \begin{align} \sum_{i=1}^{n}X_i=T_n. \end{align} $$
$$ \begin{align} \sum_{i=1}^{n}X_i=T_n. \end{align} $$
Lemma 3 One has
Proof Since
 $$ \begin{align*}\mathbb{E}(X_n^2) =\frac{\mathbb{E}\left(||q_{n}||_4^8\right)}{n^4}+\frac{\mathbb{E}\left(||q_{n-1}||_4^8\right)}{(n-1)^4} -\frac{2\mathbb{E}\left(||q_{n}||_4^4 \cdot ||q_{n-1}||_4^4 \right)}{n^2~(n-1)^2}, \end{align*} $$
$$ \begin{align*}\mathbb{E}(X_n^2) =\frac{\mathbb{E}\left(||q_{n}||_4^8\right)}{n^4}+\frac{\mathbb{E}\left(||q_{n-1}||_4^8\right)}{(n-1)^4} -\frac{2\mathbb{E}\left(||q_{n}||_4^4 \cdot ||q_{n-1}||_4^4 \right)}{n^2~(n-1)^2}, \end{align*} $$
by Lemma 2, a direct calculation yields the assertion, as desired.
Lemma 4 Let
![]() $i,j$
be positive integers such that
$i,j$
be positive integers such that
![]() $1<i<j<\infty $
. Then
$1<i<j<\infty $
. Then
 $$ \begin{align} \big|\mathbb{E}(X_i X_j)\big|\leq C\frac{j^5}{(i-1)^8}, \end{align} $$
$$ \begin{align} \big|\mathbb{E}(X_i X_j)\big|\leq C\frac{j^5}{(i-1)^8}, \end{align} $$
where C is a constant independent of
![]() $i,j$
.
$i,j$
.
Proof Observe that
 $$ \begin{align*} \mathbb{E}( X_i X_j) =&\frac{\mathbb{E}\big(||q_i||_4^4\cdot ||q_j||_4^4\big)}{i^2 j^2}-\frac{\mathbb{E}\big(||q_i||_4^4\cdot ||q_{j-1}||_4^4\big)}{i^2 (j-1)^2}\\ &-\frac{\mathbb{E}\big(||q_{i-1}||_4^4\cdot ||q_j||_4^4\big)}{(i-1)^2 j^2}+\frac{\mathbb{E}\big(||q_{i-1}||_4^4\cdot ||q_{j-1}||_4^4\big)}{(i-1)^2 (j-1)^2}. \end{align*} $$
$$ \begin{align*} \mathbb{E}( X_i X_j) =&\frac{\mathbb{E}\big(||q_i||_4^4\cdot ||q_j||_4^4\big)}{i^2 j^2}-\frac{\mathbb{E}\big(||q_i||_4^4\cdot ||q_{j-1}||_4^4\big)}{i^2 (j-1)^2}\\ &-\frac{\mathbb{E}\big(||q_{i-1}||_4^4\cdot ||q_j||_4^4\big)}{(i-1)^2 j^2}+\frac{\mathbb{E}\big(||q_{i-1}||_4^4\cdot ||q_{j-1}||_4^4\big)}{(i-1)^2 (j-1)^2}. \end{align*} $$
Without loss of generality, we assume that i is even. Following similar arguments in the proof of Lemma 2, we obtain the following:
-
•
 $\mathbb {E}(||q_i||_4^4\cdot ||q_j||_4^4)=4A_i^2 A_j^2+2jA_i^2+2iA_j^2+ij+4i^2-8i+\frac {16}{3}i^3-24i^2+\frac {80}{3}i,$
$\mathbb {E}(||q_i||_4^4\cdot ||q_j||_4^4)=4A_i^2 A_j^2+2jA_i^2+2iA_j^2+ij+4i^2-8i+\frac {16}{3}i^3-24i^2+\frac {80}{3}i,$
-
•
 $\mathbb {E}(||q_i||_4^4\cdot ||q_{j-1}||_4^4)\,=\,4A_i^2 A_{j-1}^2\,+\,2(j-1)A_i^2\,+\,2iA_{j-1} ^2+i(j-1)+4i^2-8i +\frac {16}{3}i^3-24i^2+\frac {80}{3}i,$
$\mathbb {E}(||q_i||_4^4\cdot ||q_{j-1}||_4^4)\,=\,4A_i^2 A_{j-1}^2\,+\,2(j-1)A_i^2\,+\,2iA_{j-1} ^2+i(j-1)+4i^2-8i +\frac {16}{3}i^3-24i^2+\frac {80}{3}i,$
-
•
 $\mathbb {E}(||q_{i-1}||_4^4\cdot ||q_j||_4^4) {\kern-1pt}={\kern-1pt}4A_{i-1}^2 A_j^2{\kern-1pt}+{\kern-1pt}2jA_{i-1}^2+2(i-1)A_j^2+(i-1)j +4(i-1)^2-8(i-1) +4+\frac {16}{3}(i-1)^3-24(i-1)^2+\frac {80}{3}(i-1)-8,$
$\mathbb {E}(||q_{i-1}||_4^4\cdot ||q_j||_4^4) {\kern-1pt}={\kern-1pt}4A_{i-1}^2 A_j^2{\kern-1pt}+{\kern-1pt}2jA_{i-1}^2+2(i-1)A_j^2+(i-1)j +4(i-1)^2-8(i-1) +4+\frac {16}{3}(i-1)^3-24(i-1)^2+\frac {80}{3}(i-1)-8,$
-
•
 $\mathbb {E}(||q_{i-1}||_4^4\cdot ||q_{j-1}||_4^4)\, =\,4A_{i-1}^2 A_{j-1}^2\,+\,2(j-1)A_{i-1}^2+2(i-1)A_{j-1}^2+(i-1)(j-1) +4(i-1)^2-8(i-1)+4+\frac {16}{3}(i-1)^3-24(i-1)^2+\frac {80}{3}(i-1)-8.$
$\mathbb {E}(||q_{i-1}||_4^4\cdot ||q_{j-1}||_4^4)\, =\,4A_{i-1}^2 A_{j-1}^2\,+\,2(j-1)A_{i-1}^2+2(i-1)A_{j-1}^2+(i-1)(j-1) +4(i-1)^2-8(i-1)+4+\frac {16}{3}(i-1)^3-24(i-1)^2+\frac {80}{3}(i-1)-8.$
Therefore, we have
 $$ \begin{align*} \mathbb{E}( X_i X_j) =\frac{-\frac{32}{3}i^4 j +\frac{64}{3}i^3 j +i^2 j^2+\frac{16}{3}i^4-\frac{32}{3}i^3-ij^2+\frac{53}{3}i^2j-\frac{28}{3}i^2-\frac{109}{3}ij+\frac{56}{3}i}{i^2 j^2 (i-1)^2 (j-1)^2}. \end{align*} $$
$$ \begin{align*} \mathbb{E}( X_i X_j) =\frac{-\frac{32}{3}i^4 j +\frac{64}{3}i^3 j +i^2 j^2+\frac{16}{3}i^4-\frac{32}{3}i^3-ij^2+\frac{53}{3}i^2j-\frac{28}{3}i^2-\frac{109}{3}ij+\frac{56}{3}i}{i^2 j^2 (i-1)^2 (j-1)^2}. \end{align*} $$
Bearing in mind
![]() $i<j$
, we deduce (11). A similar reasoning leads to the proof when i is odd. The proof is complete now.
$i<j$
, we deduce (11). A similar reasoning leads to the proof when i is odd. The proof is complete now.
3 Proof of Theorem 1
In this section we prove the main theorem. We first introduce some probabilistic tools involved in the proof of Theorem 1. The first lemma is a general method for establishing almost sure convergence, known as the method of subsequences.
Lemma 5 [Reference Stout27]
Let
![]() $\{Y_n\}_{n=1}^{\infty }$
be a sequence of random variables. Suppose that there exist a random variable Y and an increasing sequence of positive integers
$\{Y_n\}_{n=1}^{\infty }$
be a sequence of random variables. Suppose that there exist a random variable Y and an increasing sequence of positive integers
![]() $\{n_k\}_{k=1}^{\infty }$
such that
$\{n_k\}_{k=1}^{\infty }$
such that
and
Then
The next lemma is the so-called Serfling’s maximal inequality. Let
![]() $\{\xi _n\}_{n=1}^{\infty }$
be a sequence of random variables. For each
$\{\xi _n\}_{n=1}^{\infty }$
be a sequence of random variables. For each
![]() $a\geq 0$
and
$a\geq 0$
and
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $F_{a,n}$
be the joint distribution function of
$F_{a,n}$
be the joint distribution function of
![]() $\xi _{a+1}, \ldots , \xi _{a+n}$
, that is,
$\xi _{a+1}, \ldots , \xi _{a+n}$
, that is,
for each
![]() $(x_1, x_2, \ldots , x_n)\in \mathbb {R}^n$
. Let
$(x_1, x_2, \ldots , x_n)\in \mathbb {R}^n$
. Let
 $$ \begin{align*}M_{a,n}=\max_{a<k\leq n}~\bigg|\sum_{i=a+1}^{a+k} \xi_i \bigg|.\end{align*} $$
$$ \begin{align*}M_{a,n}=\max_{a<k\leq n}~\bigg|\sum_{i=a+1}^{a+k} \xi_i \bigg|.\end{align*} $$
Then, Serfling’s maximal inequality provides a good upper bound for
![]() $\mathbb {E} M_{a,n}^2$
.
$\mathbb {E} M_{a,n}^2$
.
Lemma 6 [Reference Stout27]
Suppose that g is a nonnegative functional defined on the collection of joint distribution functions such that
for all
![]() $1\leq k<k+m$
and
$1\leq k<k+m$
and
![]() $a\geq 0$
,
$a\geq 0$
,
 $$ \begin{align*}\mathbb{E} \bigg( \sum_{i=a+1}^{a+n} \xi_i \bigg)^2\leq g(F_{a,n})\end{align*} $$
$$ \begin{align*}\mathbb{E} \bigg( \sum_{i=a+1}^{a+n} \xi_i \bigg)^2\leq g(F_{a,n})\end{align*} $$
for all
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $a\geq 0$
. Then
$a\geq 0$
. Then
 $$ \begin{align*} \mathbb{E} M_{a,n}^2\leq \left(\frac{\log(2n)}{\log 2}\right)^2 g(F_{a,n}) \end{align*} $$
$$ \begin{align*} \mathbb{E} M_{a,n}^2\leq \left(\frac{\log(2n)}{\log 2}\right)^2 g(F_{a,n}) \end{align*} $$
for all
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $a\geq 0.$
$a\geq 0.$
Remark It is perhaps clear that the choice of the nonnegative functional g is the crucial part when applying Serfling’s maximal inequality.
The following lemma follows from the Chebyshev inequality and the Borel–Cantelli lemma.
Lemma 7 [Reference Stout27]
Let
![]() $\{\xi _n\}_{n=1}^{\infty }$
be a sequence of random variables. Suppose that
$\{\xi _n\}_{n=1}^{\infty }$
be a sequence of random variables. Suppose that
 $$ \begin{align*}\sum_{n=1}^{\infty}\mathbb{E}|\xi_n|^p<\infty\end{align*} $$
$$ \begin{align*}\sum_{n=1}^{\infty}\mathbb{E}|\xi_n|^p<\infty\end{align*} $$
for some
![]() $p>0$
. Then
$p>0$
. Then
The following lemma provides a sufficient condition for almost sure convergence, with the main component of its proof being the Borel–Cantelli lemma.
Lemma 8 [Reference Cinlar9, Proposition 2.6, p. 98]
Suppose that
 $$ \begin{align*}\sum_{n=1}^{\infty}\mathbb{P}(|\xi_n-\xi|>\varepsilon)<\infty\end{align*} $$
$$ \begin{align*}\sum_{n=1}^{\infty}\mathbb{P}(|\xi_n-\xi|>\varepsilon)<\infty\end{align*} $$
for any
![]() $\varepsilon>0$
. Then
$\varepsilon>0$
. Then
![]() $\xi _n \rightarrow \xi $
almost surely.
$\xi _n \rightarrow \xi $
almost surely.
Now we are ready to prove Theorem 1.
Proof of Theorem 1
Set
![]() $T_n=||q_n||_4^4/n^2$
for any positive integer n. The key to the proof is the following:
$T_n=||q_n||_4^4/n^2$
for any positive integer n. The key to the proof is the following:
 $$ \begin{align} \sum_{k=1}^{\infty}\mathbb{E}\left(\max\limits_{2^{k-1}<n\leq 2^k}\big|T_n-T_{2^{k-1}}\big|^2\right)<\infty. \end{align} $$
$$ \begin{align} \sum_{k=1}^{\infty}\mathbb{E}\left(\max\limits_{2^{k-1}<n\leq 2^k}\big|T_n-T_{2^{k-1}}\big|^2\right)<\infty. \end{align} $$
Given the above estimate, the proof can be completed by the method of subsequences as follows. By Markov’s inequality and Lemma 2, we have
 $$ \begin{align*} \sum_{k=1}^{\infty} \mathbb{P}\big\{\big|T_{2^k}-2\big|>\varepsilon \big\} &\leq\frac{1}{\varepsilon^2}\sum_{k=1}^{\infty}\mathbb{E}\big(T_{2^k}-2)^2\\ &= \frac{1}{\varepsilon^2} \sum_{k=1}^{\infty} \left(\frac{16}{3\cdot 2^k}+O\left(\frac{1}{2^{2k}}\right) \right),\end{align*} $$
$$ \begin{align*} \sum_{k=1}^{\infty} \mathbb{P}\big\{\big|T_{2^k}-2\big|>\varepsilon \big\} &\leq\frac{1}{\varepsilon^2}\sum_{k=1}^{\infty}\mathbb{E}\big(T_{2^k}-2)^2\\ &= \frac{1}{\varepsilon^2} \sum_{k=1}^{\infty} \left(\frac{16}{3\cdot 2^k}+O\left(\frac{1}{2^{2k}}\right) \right),\end{align*} $$
which together with Lemma 8 implies
In addition, combining (12) and Lemma 7, we get
It follows from Lemma 5, (13), and (14) that
as desired.
Now it remains to prove (12). To accomplish this, we use Serfling’s maximal inequality. Recall that
![]() $X_n:= T_n-T_{n-1}$
. For each
$X_n:= T_n-T_{n-1}$
. For each
![]() $a\geq 0$
and
$a\geq 0$
and
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $F_{a,n}$
be the joint distribution function of
$F_{a,n}$
be the joint distribution function of
![]() $X_{a+1}, \ldots , X_{a+n}$
, and
$X_{a+1}, \ldots , X_{a+n}$
, and
![]() $M_{a,n}$
be defined by
$M_{a,n}$
be defined by
 $$ \begin{align} M_{a,n}=\max\limits_{1\leq k\leq n}\left|\sum_{i=a+1}^{a+k}X_i \right|. \end{align} $$
$$ \begin{align} M_{a,n}=\max\limits_{1\leq k\leq n}\left|\sum_{i=a+1}^{a+k}X_i \right|. \end{align} $$
Now we need to construct an appropriate nonnegative functional g, defined on the collection of joint distribution functions, which, after some experimentation, we opt to be
 $$ \begin{align} g(F_{a,n})=\sum_{i=a+1}^{a+n} \mathbb{E}(X_i^2)+2\sum_{i=a+1}^{a+n-1}\sum_{j=i+1}^{a+n}\big|\mathbb{E}(X_i X_j)\big|. \end{align} $$
$$ \begin{align} g(F_{a,n})=\sum_{i=a+1}^{a+n} \mathbb{E}(X_i^2)+2\sum_{i=a+1}^{a+n-1}\sum_{j=i+1}^{a+n}\big|\mathbb{E}(X_i X_j)\big|. \end{align} $$
Then, a direct calculation shows that the following (17) and (18) hold:
and
 $$ \begin{align} \mathbb{E}\bigg(\sum_{i=a+1}^{a+n} X_i \bigg)^2\leq g(F_{a,n}) \end{align} $$
$$ \begin{align} \mathbb{E}\bigg(\sum_{i=a+1}^{a+n} X_i \bigg)^2\leq g(F_{a,n}) \end{align} $$
for all
![]() $a\geq 0$
,
$a\geq 0$
,
![]() $1\leq k<k+m$
and
$1\leq k<k+m$
and
![]() $n\geq 1$
. Thus, by Lemma 6, we obtain
$n\geq 1$
. Thus, by Lemma 6, we obtain
 $$ \begin{align} \mathbb{E}\left(M_{a,n}^2 \right)\leq\left(\frac{\log{(2n)}}{\log{2}}\right)^2 g(F_{a,n}). \end{align} $$
$$ \begin{align} \mathbb{E}\left(M_{a,n}^2 \right)\leq\left(\frac{\log{(2n)}}{\log{2}}\right)^2 g(F_{a,n}). \end{align} $$
Bearing in mind (10) and combining (15), (16), and (19), we deduce that
 $$ \begin{align*} &\sum_{k=1}^{\infty}\mathbb{E}\left(\max\limits_{2^{k-1}<n\leq 2^k}\big| T_n-T_{2^{k-1}}\big|^2\right)\\ &\quad\leq\sum_{k=1}^{\infty}k^2 \left(\sum_{i=2^{k-1}+1}^{2^k} \mathbb{E}(X_i^2) +2\sum_{i=2^{k-1}+1}^{2^k-1}\sum_{j=i+1}^{2^k}\big|\mathbb{E}(X_i X_j)\big|\right). \end{align*} $$
$$ \begin{align*} &\sum_{k=1}^{\infty}\mathbb{E}\left(\max\limits_{2^{k-1}<n\leq 2^k}\big| T_n-T_{2^{k-1}}\big|^2\right)\\ &\quad\leq\sum_{k=1}^{\infty}k^2 \left(\sum_{i=2^{k-1}+1}^{2^k} \mathbb{E}(X_i^2) +2\sum_{i=2^{k-1}+1}^{2^k-1}\sum_{j=i+1}^{2^k}\big|\mathbb{E}(X_i X_j)\big|\right). \end{align*} $$
Set
 $$ \begin{align*} \text{I}:=\sum_{k=1}^{\infty} k^2\sum_{i=2^{k-1}+1}^{2^k} \mathbb{E}(X_i^2) \end{align*} $$
$$ \begin{align*} \text{I}:=\sum_{k=1}^{\infty} k^2\sum_{i=2^{k-1}+1}^{2^k} \mathbb{E}(X_i^2) \end{align*} $$
and
 $$ \begin{align*} \text{II}:=\sum_{k=1}^{\infty} k^2 \sum_{i=2^{k-1}+1}^{2^k-1}\sum_{j=i+1}^{2^k}\big|\mathbb{E}(X_i X_j)\big|. \end{align*} $$
$$ \begin{align*} \text{II}:=\sum_{k=1}^{\infty} k^2 \sum_{i=2^{k-1}+1}^{2^k-1}\sum_{j=i+1}^{2^k}\big|\mathbb{E}(X_i X_j)\big|. \end{align*} $$
Next we show that both I and II are finite. Note that
 $$ \begin{align} \text{I}\asymp\sum_{k=2}^{\infty}(\log k)^2 \mathbb{E}(X_k^2), \end{align} $$
$$ \begin{align} \text{I}\asymp\sum_{k=2}^{\infty}(\log k)^2 \mathbb{E}(X_k^2), \end{align} $$
so by Lemma 3, we get
![]() $\text {I}<\infty $
. In addition, Lemma 4 yields
$\text {I}<\infty $
. In addition, Lemma 4 yields
 $$ \begin{align*} \text{II}\leq C\sum_{k=1}^{\infty}k^2 \sum_{i=2^{k-1}+1}^{2^k-1}\sum_{j=i+1}^{2^k} \frac{j^5}{(i-1)^8}<\infty, \end{align*} $$
$$ \begin{align*} \text{II}\leq C\sum_{k=1}^{\infty}k^2 \sum_{i=2^{k-1}+1}^{2^k-1}\sum_{j=i+1}^{2^k} \frac{j^5}{(i-1)^8}<\infty, \end{align*} $$
which together with (20) implies (12). This completes the proof.
4 Extension for general random variables
In this section, we extend Theorem 1 to encompass a much more general case, requiring only an assumption on the fourth moment. The main new ingredient is Doob’s maximal inequality instead of Serfling’s.
Theorem 9 Let
![]() $p_n(z)=\sum _{k=0}^{n-1}\epsilon _k z^k$
, where the random variables
$p_n(z)=\sum _{k=0}^{n-1}\epsilon _k z^k$
, where the random variables
![]() $\{\epsilon _k, k\geq 0\}$
are independent and identically distributed, with mean
$\{\epsilon _k, k\geq 0\}$
are independent and identically distributed, with mean
![]() $0$
, variance
$0$
, variance
![]() $\sigma ^2$
and a finite fourth moment
$\sigma ^2$
and a finite fourth moment
![]() $\mathbb {E}(\epsilon _k^4)<\infty $
. Then
$\mathbb {E}(\epsilon _k^4)<\infty $
. Then
 $$ \begin{align*} \frac{||p_n||_4}{\sqrt{n}}\rightarrow \sqrt[4]{2}\cdot\sigma \end{align*} $$
$$ \begin{align*} \frac{||p_n||_4}{\sqrt{n}}\rightarrow \sqrt[4]{2}\cdot\sigma \end{align*} $$
almost surely.
Proof Analogous to (3), we observe that
 $$ \begin{align} ||p_n||_4^4 =\sum\limits_{j+k=l+m\atop 1\leq j,k,l,m\leq n}\epsilon_j\epsilon_k\epsilon_l\epsilon_m. \end{align} $$
$$ \begin{align} ||p_n||_4^4 =\sum\limits_{j+k=l+m\atop 1\leq j,k,l,m\leq n}\epsilon_j\epsilon_k\epsilon_l\epsilon_m. \end{align} $$
Now we decompose
![]() $||p_n||_4^4$
into four parts. Let
$||p_n||_4^4$
into four parts. Let
That is, the indices
![]() $j,k,l$
, and m are mutually different from each other. Let
$j,k,l$
, and m are mutually different from each other. Let
and
 $$ \begin{align*}B_n= \sum\limits_{l+m=2j\atop 1\leq j,l,m\leq n} \epsilon_j^2 \epsilon_l \epsilon_m 1_{\{l\neq m \}}.\end{align*} $$
$$ \begin{align*}B_n= \sum\limits_{l+m=2j\atop 1\leq j,l,m\leq n} \epsilon_j^2 \epsilon_l \epsilon_m 1_{\{l\neq m \}}.\end{align*} $$
Then one has
 $$ \begin{align} \frac{||p_n||_4^4}{n^2}=\frac{M_n}{n^2}+2\frac{B_n}{n^2} +2\frac{\sum\limits_{ 1\leq j,l\leq n } \epsilon_j^2 \epsilon_l^2 1_{\{j\neq l\}} }{n^2} +\frac{\sum_{j=1}^{n} \epsilon_j^4}{n^2}. \end{align} $$
$$ \begin{align} \frac{||p_n||_4^4}{n^2}=\frac{M_n}{n^2}+2\frac{B_n}{n^2} +2\frac{\sum\limits_{ 1\leq j,l\leq n } \epsilon_j^2 \epsilon_l^2 1_{\{j\neq l\}} }{n^2} +\frac{\sum_{j=1}^{n} \epsilon_j^4}{n^2}. \end{align} $$
By the strong law of large numbers, the last term of (22) converges to 0 almost surely. In addition, the third term of (22) converges to
![]() $2\sigma ^4$
almost surely by adding
$2\sigma ^4$
almost surely by adding
![]() $2(\sum _{j=1}^{n} \epsilon _j^4)/n^2$
to it and applying SLLN again.
$2(\sum _{j=1}^{n} \epsilon _j^4)/n^2$
to it and applying SLLN again.
For the first two terms of (22), we observe that
![]() $\mathbb {E} B_n=0$
and a simple estimation yields
$\mathbb {E} B_n=0$
and a simple estimation yields
 $$ \begin{align*} \mathbb{E} (B_n^2)=2 \mathbb{E}\bigg( \sum\limits_{1\leq j,l\leq n} \epsilon^4_j \epsilon^2_l \epsilon^2_{2j-l}1_{\{j\neq l, 1\leq 2j-l\leq n \}}\bigg) =O(n^2). \end{align*} $$
$$ \begin{align*} \mathbb{E} (B_n^2)=2 \mathbb{E}\bigg( \sum\limits_{1\leq j,l\leq n} \epsilon^4_j \epsilon^2_l \epsilon^2_{2j-l}1_{\{j\neq l, 1\leq 2j-l\leq n \}}\bigg) =O(n^2). \end{align*} $$
Using Markov’s inequality, we obtain
 $$ \begin{align*}\sum_{n=1}^{\infty} \mathbb{P}(B_n^2/n^4>\delta) \lesssim \frac{1}{\delta} \sum_{n=1}^{\infty}\frac{1}{n^2}<\infty\end{align*} $$
$$ \begin{align*}\sum_{n=1}^{\infty} \mathbb{P}(B_n^2/n^4>\delta) \lesssim \frac{1}{\delta} \sum_{n=1}^{\infty}\frac{1}{n^2}<\infty\end{align*} $$
for any
![]() $\delta>0$
. Then Lemma 8 yields
$\delta>0$
. Then Lemma 8 yields
![]() $B_n/n^2\rightarrow 0$
almost surely. Lastly, for the first term of (22), we observe that the sequence
$B_n/n^2\rightarrow 0$
almost surely. Lastly, for the first term of (22), we observe that the sequence
![]() $\{M_n\}_{n\geq 1}$
forms a martingale with respect to the standard filtration
$\{M_n\}_{n\geq 1}$
forms a martingale with respect to the standard filtration
Using
![]() $\mathbb {E} M_n=0$
and the calculations leading to (i) and (ii) of Lemma 2, we have
$\mathbb {E} M_n=0$
and the calculations leading to (i) and (ii) of Lemma 2, we have
For any increasing sequence of integers
![]() $\{n_k\}_{k=1}^{\infty }$
, Doob’s maximal inequality implies that for any
$\{n_k\}_{k=1}^{\infty }$
, Doob’s maximal inequality implies that for any
![]() $\delta>0$
,
$\delta>0$
,
 $$ \begin{align*}\mathbb{P}\left(\max\limits_{n_k\leq n\leq n_{k+1}} |M_n|>n_k^2\delta\right)\leq \frac{\mathbb{E} (M_{n_{k+1}}^2) }{n_k^4 \delta^2} =O(n_{k+1}^3/n_k^4).\end{align*} $$
$$ \begin{align*}\mathbb{P}\left(\max\limits_{n_k\leq n\leq n_{k+1}} |M_n|>n_k^2\delta\right)\leq \frac{\mathbb{E} (M_{n_{k+1}}^2) }{n_k^4 \delta^2} =O(n_{k+1}^3/n_k^4).\end{align*} $$
By choosing
![]() $n_k=2^k$
, we deduce that
$n_k=2^k$
, we deduce that
 $$ \begin{align*} \sum_{k=1}^{\infty}\mathbb{P}\bigg(\max\limits_{2^k\leq n\leq 2^{k+1}} \frac{|M_n|}{n^2}>\delta\bigg) \leq&\sum_{k=1}^{\infty}\mathbb{P}\bigg(\max\limits_{2^k\leq n\leq 2^{k+1}} \frac{|M_n|}{(2^k)^2}>\delta\bigg)<\infty. \end{align*} $$
$$ \begin{align*} \sum_{k=1}^{\infty}\mathbb{P}\bigg(\max\limits_{2^k\leq n\leq 2^{k+1}} \frac{|M_n|}{n^2}>\delta\bigg) \leq&\sum_{k=1}^{\infty}\mathbb{P}\bigg(\max\limits_{2^k\leq n\leq 2^{k+1}} \frac{|M_n|}{(2^k)^2}>\delta\bigg)<\infty. \end{align*} $$
By Lemma 8, we get
which in turn implies that
![]() $M_n/n^2\rightarrow 0$
almost surely. This completes the proof.
$M_n/n^2\rightarrow 0$
almost surely. This completes the proof.
Acknowledgements
The authors thank the anonymous referee for a meticulous reading of the manuscript and for suggesting the second proof in Section 4.