Habib Muzaffar of Carleton University has pointed out to the authors that in their paper $\left[ \text{A} \right]$ only the result

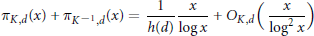$${{\pi }_{K,d}}\left( x \right)\,+\,{{\pi }_{{{K}^{-1}},d}}\left( x \right)\,=\,\frac{1}{h\left( d \right)}\,\frac{x}{\log x}\,+\,{{O}_{K,d}}\left( \frac{x}{{{\log }^{2}}x} \right)$$

follows from the prime ideal theorem with remainder for ideal classes, and not the stronger result

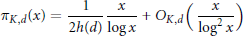$${{\pi }_{K,d}}\left( x \right)\,=\,\frac{1}{2h\left( d \right)}\,\frac{x}{\log \,x}\,+\,{{O}_{K,d}}\left( \frac{x}{{{\log }^{2}}\,x} \right)$$

stated in Lemma 5.2. This necessitates changes in Sections 5 and 6 of $\left[ \text{A} \right]$. The main results of the paper are not affected by these changes. It should also be noted that, starting on page 177 of 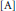$\left[ \text{A} \right]$, each and every occurrence of 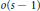$o\left( s-1 \right)$ should be replaced by 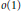$o\left( 1 \right)$.

Sections 5 and 6 of 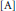$\left[ \text{A} \right]$ have been rewritten to incorporate the abovementioned correction and are given below. They should replace the original Sections 5 and 6 of 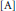$\left[ \text{A} \right]$.