Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-13T08:01:34.787Z Has data issue: false hasContentIssue false
  • English
  • Français

A Uniform Asymptotic Expansion of the Jacobi Polynomials with Error Bounds

Published online by Cambridge University Press:  20 November 2018

C. L. Frenzen  and
R. Wong
C. L. Frenzen
Affiliation:
Southern Methodist University, Dallas, Texas
R. Wong
Affiliation:
Southern Methodist University, Dallas, Texas
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

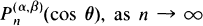In a recent investigation of the asymptotic behavior of the Lebesgue constants for Jacobi polynomials, we encountered the problem of obtaining an asymptotic expansion for the Jacobi polynomials , as n → ∞, which is uniformly valid for θ in 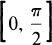. The leading term of such an expansion is provided by the following well-known formula of “Hilb's type” [13, p. 197]: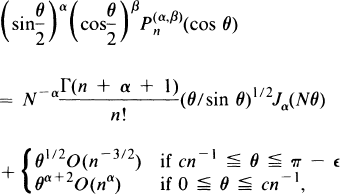

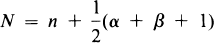(1.1)

where α > – 1, β real and ; c and are fixed positive numbers. Note that the remainder in (1.1) is always θ1/2O(n–3/2).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 5 , 01 October 1985 , pp. 979 - 1007
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Abramowitz, M. and Stegun, I., Handbook of mathematical functions, N.B.S. Applied Math. Ser. 55 (Washington, D.C., 1964).Google Scholar
2. Askey, R., Orthogonal polynomials and special functions, CBMS 21 (SIAM, Philadelphia, 1975).CrossRefGoogle Scholar
3. Askey, R., The collected papers of Gabor Szegö, Vol. 2 (Birkhauser, Cambridge, MA, 1982).CrossRefGoogle Scholar
4. Elliott, D., Uniform asymptotic expansions of the Jacobi polynomials and an associated function, Math. Comp. 25 (1971), 309–314.Google Scholar
5. Gasper, G., Formulas of the Dirichlet-Mehler type, fractional calculus and its applications 457 (Springer-Verlag Lecture Notes in Mathematics), 207–215.CrossRefGoogle Scholar
6. Gatteschi, L., Limitazione degli errori nelle formule asintotiche per le funzioni speciali, Rend. Semin. Mat. Univ. e Pol., Torino 16 (1956-1957), 83–94.Google Scholar
7. Gatteschi, L., Una nuova rappresentazione asintotica dei polinomi di Jacobi, Rend. Semin. Mat. Univ. e Pol., Torino 27 (1967-68), 165–184.Google Scholar
8. Gradshteyn, I. S. and Ryzhik, I. M., Tables of integrals, series and products (Academic Press, New York, 1965).Google Scholar
9. Hahn, E., Asymptotik bei Jacobi-Polynomen und Jacobi-Funktionen, Math. Zeit. 171 (1980), 201–226.Google Scholar
10. Olver, F. W. J., Asymptotics and special functions (Academic Press, New York, 1974).Google Scholar
11. Szegö, G., Über einige asymptotische Entwicklungen der Legendreschen Funktionen, Proc. Lond. Math. Soc. (2) 36 (1932), 427–450.Google Scholar
12. Szegö, G., Asymptotische Entwicklungen der Jacobischen Polynome, Schr. der König. Gelehr. Gesell. Naturwiss. Kl. 70 (1933), 33–112.Google Scholar
13. Szegö, G., Orthogonal polynomials, Colloquium Publications (American Mathematical Society, Providence, R.I., 1967).Google Scholar
14. Watson, G. N., A treatise on the theory of Bessel functions (Cambridge University Press, Cambridge, 1944).Google Scholar