Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Assem, Ibrahim
and
Skowroński, Andrzej
1987.
Iterated tilted algebras of type $$\tilde {\mathbb{A}}_n $$.
Mathematische Zeitschrift,
Vol. 195,
Issue. 2,
p.
269.
Asensio, P.A. Guil
and
Asensio, F. Guil
1992.
On torsion theories induced by tilting modules.
Communications in Algebra,
Vol. 20,
Issue. 7,
p.
2015.
Assem, Ibrahim
and
Kerner, Otto
1993.
Tilting modules and a theorem of Hoshino.
Glasgow Mathematical Journal,
Vol. 35,
Issue. 1,
p.
69.
Rump, Wolfgang
2001.
*-MODULES, TILTING, AND ALMOST ABELIAN CATEGORIES.
Communications in Algebra,
Vol. 29,
Issue. 8,
p.
3293.
Coelho, Flávio Ulhoa
Happel, Dieter
and
Unger, Luise
2002.
Tilting up algebras of small homological dimensions.
Journal of Pure and Applied Algebra,
Vol. 174,
Issue. 3,
p.
219.
Kerner, Otto
and
Trlifaj, Jan
2005.
Tilting classes over wild hereditary algebras.
Journal of Algebra,
Vol. 290,
Issue. 2,
p.
538.
Kerner, Otto
and
Trlifaj, Jan
2007.
Constructing tilting modules.
Transactions of the American Mathematical Society,
Vol. 360,
Issue. 4,
p.
1907.
Assem, Ibrahim
Coelho, Flávio U.
and
Trepode, Sonia
2009.
Contravariantly finite subcategories closed under predecessors.
Journal of Algebra,
Vol. 322,
Issue. 4,
p.
1196.
Iyama, Osamu
and
Reiten, Idun
2014.
Introduction to τ-tilting theory.
Proceedings of the National Academy of Sciences,
Vol. 111,
Issue. 27,
p.
9704.
Li, Yuan
and
Yao, Hailou
2021.
Tilting Torsion-Free Classes in the Category of Comodules.
Bulletin of the Iranian Mathematical Society,
Vol. 47,
Issue. 2,
p.
553.
2023.
Modern Trends in Algebra and Representation Theory.
p.
46.
Argudín-Monroy, Alejandro
and
Mendoza-Hernández, Octavio
2025.
Relative tilting theory in abelian categories II: n-$$\mathcal {X}$$-tilting theory.
Boletín de la Sociedad Matemática Mexicana,
Vol. 31,
Issue. 2,
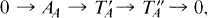
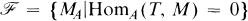 and
and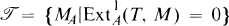
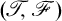 on modA[8]. The aim of the present paper is to find conditions on a torsion theory in order that it be induced by a tilting module.
on modA[8]. The aim of the present paper is to find conditions on a torsion theory in order that it be induced by a tilting module.