Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T00:43:17.775Z Has data issue: false hasContentIssue false
  • English
  • Français

Three Test Problems for Quasisimilarity

Published online by Cambridge University Press:  20 November 2018

Hari Bercovici
Hari Bercovici*
Affiliation:
Indiana University, Bloomington, Indiana
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Kaplansky proposed in [7] three problems with which to test the adequacy of a proposed structure theory of infinite abelian groups. These problems can be rephrased as test problems for a structure theory of operators on Hilbert space. Thus, R. Kadison and I. Singer answered in [6] these test problems for the unitary equivalence of operators. We propose here a study of these problems for quasisimilarity of operators on Hilbert space. We recall first that two (bounded, linear) operators T and T′ acting on the Hilbert spaces and 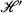, are said to be quasisimilar if there exist bounded operators and with densely defined inverses, satisfying the relations T′X = XT and TY = YT′. The fact that T and T′ are quasisimilar is indicated by T ∼ T′. The problems mentioned above can now be formulated as follows.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 4 , 01 August 1987 , pp. 880 - 892
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Bercovici, H., On the Jordan model of C0 operators (I). Studia Math. 60 (1977), 267–284; II , Acta Sci. Math. (Szeged) 42 (1980), 43–56.Google Scholar
2. Bercovici, H., C0-Fredholm operators. II, Acta Sci. Math. (Szeged) 42 (1980), 3–42.Google Scholar
3. Bercovici, H., Foias, C. and Sz.-Nagy, B., Compléments à l'étude des opérateurs de classe C0. III Acta Sci. Math. (Szeged) 37 (1975), 313–322.Google Scholar
4. Bercovici, H. and Voiculescu, D., Tensor operations on characteristic functions of C0 contractions, Acta Sci. Math. (Szeged) 39 (1977), 205–231.Google Scholar
5. Duren, P. L., Theory of Hp spaces (Academic Press, New York, 1970).Google Scholar
6. Kadison, R. V. and Singer, I. M., Three test problems in operator theory, Pacific J. Math. 7 (1957), 1101–1106.Google Scholar
7. Kaplansky, I., Infinite abelian groups (Michigan University Press, Ann Arbor, 1955).Google Scholar
8. Sz.-Nagy, B. and Foias, C., Harmonic analysis of operators on Hilbert space (North Holland, Amsterdam, 1970).Google Scholar
9. Sz.-Nagy, B. and Foias, C., On injections intertwining operators of class C0 , Acta Sci. Math. (Szeged) 40 (1978), 163–167.Google Scholar