Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T10:04:09.324Z Has data issue: false hasContentIssue false
  • English
  • Français

Tensor Product Realizations of Simple Torsion Free Modules

Published online by Cambridge University Press:  20 November 2018

D. J. Britten  and
F. W. Lemire
D. J. Britten
Affiliation:
Department of Mathematics University of Windsor Windsor, Ontario N9B 3P4
F. W. Lemire
Affiliation:
Department of Mathematics University of Windsor Windsor, Ontario N9B 3P4
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

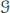Let $\mathcal{G}$ be a finite dimensional simple Lie algebra over the complex numbers $C$. Fernando reduced the classification of infinite dimensional simple 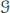$\mathcal{G}$-modules with a finite dimensional weight space to determining the simple torsion free 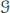$\mathcal{G}$-modules for 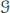$\mathcal{G}$ of type 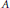$A$ or $C$. These modules were determined by Mathieu and using his work we provide a more elementary construction realizing each one as a submodule of an easily constructed tensor product module.

Keywords

17B10
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 53 , Issue 2 , 01 April 2001 , pp. 225 - 243
Copyright
Copyright © Canadian Mathematical Society 2001

References

[BBL] Benkart, G. M., Britten, D. J. and Lemire, F. W., Modules with Bounded Weight Multiplicities for Simple Lie Algebras. Math. Z. 225 (1997), 333–353.Google Scholar
[BL1] Britten, D. J. and Lemire, F. W., The Torsion Free Pieri Formula. Canad. J. Math. 50 (1998), 266–289.Google Scholar
[BL2] Britten, D. J. and Lemire, F. W., A classification of simple Lie modules having a 1-dimensional weight space. Trans. Amer. Math. Soc. 299 (1987), 683–697.Google Scholar
[BHL] Britten, D. J., Hooper, J. and Lemire, F. W., Simple Cn-modules with multiplicities 1 and applications. Canad. J. Phys. 72 (1994), 326–335.Google Scholar
[F] Fernando, S. L., Lie algebra modules with finite dimensional weight spaces. Trans. Amer.Math. Soc. 322 (1990), 757–781.Google Scholar
[L] Lemire, F. W., Infinite Dimensional Lie Modules. Queen's Papers in Pure and Appl. Math. 94 (1994), 67–72.Google Scholar
[M] Mathieu, O., Classification of Irreducible Weight Modules. Preprint.Google Scholar