Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-22T16:19:50.288Z Has data issue: false hasContentIssue false
  • English
  • Français

Symplectic Geometry of the Moduli Space of Flat Connections on a Riemann Surface: Inductive Decompositions and Vanishing Theorems

Published online by Cambridge University Press:  20 November 2018

Lisa C. Jeffrey  and
Jonathan Weitsman
Lisa C. Jeffrey
Affiliation:
Mathematics Department, University of Toronto, Toronto, Ontario, M5S 3G3
Jonathan Weitsman
Affiliation:
Mathematics Department, University of California, Santa Cruz, California 95064, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper treats the moduli space 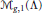${{\mathcal{M}}_{g,1}}(\Lambda)$ of representations of the fundamental group of a Riemann surface of genus $g$ with one boundary component which send the loop around the boundary to an element conjugate to exp 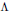$\Lambda$, where 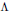$\Lambda$ is in the fundamental alcove of a Lie algebra. We construct natural line bundles over 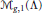${{\mathcal{M}}_{g,1}}(\Lambda)$ and exhibit natural homology cycles representing the Poincaré dual of the first Chern class. We use these cycles to prove differential equations satisfied by the symplectic volumes of these spaces. Finally we give a bound on the degree of a nonvanishing element of a particular subring of the cohomology of the moduli space of stable bundles of coprime rank $k$ and degree 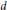$d$.

Keywords

58F05
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 3 , 01 June 2000 , pp. 582 - 612
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Atiyah, M. F. and Bott, R., The Yang-Mills equations over Riemann surfaces . Philos. Trans. Roy. Soc. London A308(1982), 523–615.Google Scholar
[2] Berline, N., Getzler, E. and Vergne, M., Heat Kernels and Dirac Operators. Grundlehren Math. Wiss. 298, Springer-Verlag, 1992.Google Scholar
[3] Bott, R. and Tu, L., Differential forms in algebraic topology. Graduate Texts in Math. 82, Springer-Verlag, 1982.Google Scholar
[4] Donaldson, S. K., Gluing techniques in the cohomology of moduli spaces . In: Topological methods in modern mathematics (Stony Brook, NY, 1991), Publish or Perish, 1993, 137–170.Google Scholar
[5] Duistermaat, J. J. and Heckman, G., On the variation in the cohomology of the symplectic form of the reduced phase space. Invent.Math. 69(1982), 259–268. Addendum, 72(1983), 153–158.Google Scholar
[6] Earl, R., The Mumford relations, and the moduli of rank three stable bundles. Compositio Math. 109(1997), 13–48.Google Scholar
[7] Earl, R. and Kirwan, F. C., The Pontryagin rings of the moduli spaces of arbitrary rank holomorphic bundles over a Riemann surface. Preprint alg-geom/9709012v1, 1996; Proc. LondonMath. Soc., to appear.Google Scholar
[8] Guillemin, V. and Kalkman, J., The Jeffrey-Kirwan localization theorem and residue operations in equivariant cohomology. J. Reine Angew. Math. 470(1996), 123–142.Google Scholar
[9] Guillemin, V. and Sternberg, S., The coefficients of the Duistermaat-Heckman polynomial and the cohomology ring of reduced spaces . In: Geometry, topology and physics (Conference Proceedings Lecture Notes in Geometry and Topology VI), International Press, 1995, 203–213.Google Scholar
[10] Guruprasad, K., Huebschmann, J., Jeffrey, L. and Weinstein, A., Group systems, groupoids, and moduli spaces of parabolic bundles. Duke Math. J. 89(1997), 377–412.Google Scholar
[11] Helgason, S., Differential Geometry, Lie Groups and Symmetric Spaces . Academic Press, 1978.Google Scholar
[12] Huebschmann, J., Symplectic and Poisson structures of certain moduli spaces I. Duke Math. J. 80(1995), 737–756. Symplectic and Poisson structures of certain moduli spaces II. Projective representations of cocompact planar discrete groups. Duke Math. J. 80(1995), 757–770.Google Scholar
[13] Huebschmann, J., On the variation of the Poisson structures of certain moduli spaces. Preprint dg-ga/9710033.Google Scholar
[14] Jeffrey, L. C., Extended moduli spaces of flat connections on Riemann surfaces. Math. Ann. 298(1994), 667–692.Google Scholar
[15] Jeffrey, L. C., Group cohomology construction of the cohomology of moduli spaces of flat connections on 2-manifolds. Duke Math. J. 77(1995), 407–429.Google Scholar
[16] Jeffrey, L. C., Symplectic forms on moduli spaces of flat connections on 2-manifolds . In: Proc. of the Georgia International Topology Conference (Athens, GA, 1993) (ed. Kazez, W.), AMS/IP Studies in Advanced Mathematics, 2(1997), Part I, 268–281.Google Scholar
[17] Jeffrey, L. C. and Kirwan, F. C., Localization for nonabelian group actions. Topology 34(1995), 291–327.Google Scholar
[18] Jeffrey, L. C. and Kirwan, F. C., Intersection pairings in moduli spaces of vector bundles of arbitrary rank on a Riemann surface. Ann. of Math. 148(1998), 109–196.Google Scholar
[19] Jeffrey, L. C. and Weitsman, J., Bohr-Sommerfeld orbits in the moduli space of flat connections and the Verlinde formula. Comm. Math. Phys. 150(1992), 593–630.Google Scholar
[20] Jeffrey, L. C. and Weitsman, J., Toric structures on the moduli space of flat connections on a Riemann surface: volumes and the moment map. Adv. Math. 106(1994), 151–168.Google Scholar
[21] Jeffrey, L. C. and Weitsman, J., Toric structures on the moduli space of flat connections on a Riemann surface II: Inductive decomposition of the moduli space. Math. Ann. 307(1997), 93–108.Google Scholar
[22] Jeffrey, L. C. and Weitsman, J., Symplectic geometry of the classical and quantum representation ring. In preparation.Google Scholar
[23] Karshon, Y., Moment maps and non-compact cobordisms . J. Differential Geom. 49(1998), 183–201.Google Scholar
[24] Liu, K., Heat Kernel and Moduli Spaces II. Math. Res. Lett. 4(1997), 569–588.Google Scholar
[25] Mehta, V. B. and Seshadri, C. S., Moduli of vector bundles on curves with parabolic structures. Math. Ann. 248(1980), 205–239.Google Scholar
[26] Ne’eman, A., The topology of quotient varieties. Ann. Math. 122(1985), 419–459.Google Scholar
[27] Newstead, P., Characteristic classes of stable bundles of rank 2 over an algebraic curve. Trans. Amer.Math. Soc. 169(1972), 337–345.Google Scholar
[28] Pnevmatikos, S., Structures symplectiques singulières génériques. Ann. Inst. Fourier (3) 34(1984), 201–218.Google Scholar
[29] Pressley, A. and Segal, G., Loop Groups . Oxford University Press, 1986.Google Scholar
[30] Varadarajan, V., Lie Groups, Lie Algebras and Their Representations. Graduate Texts in Math. 102, Springer-Verlag, 1984.Google Scholar
[31] Weitsman, J., Geometry of the intersection ring of the moduli space of flat connections and the conjectures of Newstead andWitten. Topology 37(1998), 115–132.Google Scholar
[32] Witten, E., On quantum gauge theories in two dimensions. Commun.Math. Phys. 141(1991), 153–209.Google Scholar
[33] Witten, E., Two dimensional gauge theories revisited. reprint hep-th/9204083; PJ. Geom. Phys. 9(1992), 303–368.Google Scholar