Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T01:08:54.484Z Has data issue: false hasContentIssue false
  • English
  • Français

Sur Le Théoréme De Lebesgue-Nikodym (V)

Published online by Cambridge University Press:  20 November 2018

Jean Dieudonné
Jean Dieudonné*
Affiliation:
Université de Nancy
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

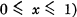Soient E un espace compact (par exemple l' intervalle et μ une mesure de Radon sur E. Une fonction numérique f intégrable pour μ définit une mesure 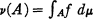sur l'ensemble des parties mesurables (pour μ) de E. On peut aussi considérer la forme linéaire 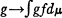qu'elle définit sur l'espace C des fonctions numériques continues dans E, et cette forme linéaire est continue pour la topologie définie par la norme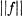 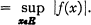. Si on appelle encore “mesure” une forme linéaire continue sur C, le théoréme de Lebesgue-Nikodym classique caractérise celles de ces “mesures” forme qui sont de la 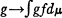. par une condition de “continuité absolue” par rapport à μ.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 3 , 1951 , pp. 129 - 139
Copyright
Copyright © Canadian Mathematical Society 1951

References

[1] Banach, S., Théorie des opérations linéaires (Warszawa, 1932).Google Scholar
[2] Birkhoff, G., Integration of functions with values in a Banach space, Trans. Amer. Math. Soc.,t.38 (1935), 357–378.Google Scholar
[3] Day, M., Some uniformly convex spaces. Bull. Amer. Math. Soc., t.47 (1941), 504–507.Google Scholar
[4] Dieudonné, J., Sur le théoréme de Lebesgue-Nikodym (III), Annales de l'Université de Grenoble, t.23 (1947-48), 25–53.Google Scholar
[5] Dieudonné, J., Sur le théoréme de Lebesgue-Nikodym (IV), J. Indian Math. Soc., 1951.Google Scholar
[6] Dieudonné, J., Sur les espaces de Köthe, Journal d'Analyse mathématique, 1951.Google Scholar
[7] Dixmier, J., Sur un théorème de Banach, Duke Math, J., t.15 (1948), 1057–1071.Google Scholar
[8] Dunford, N., Uniformity in linear spaces, Trans. Amer. Math. Soc., t.44 (1938),305–356.Google Scholar
[9] Pettis, B. J., On integration in vector spaces, Trans. Amer. Math. Soc., t.44 (1938), 277–304.Google Scholar