Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T01:59:03.393Z Has data issue: false hasContentIssue false
  • English
  • Français

Subgroups of the Power Semigroup of a Finite Semigroup

Published online by Cambridge University Press:  20 November 2018

Mohan S. Putcha
Mohan S. Putcha*
Affiliation:
North Carolina State University, Raleigh, North Carolina
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

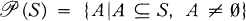Throughout this paper, S will denote a finite semigroup and Z+ the set of positive integers. E = E(S) denotes the set of idempotents of S. Let . If 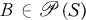, then let AB = {ab| a ∈ A, b ∈ B}. 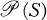has been studied by many authors, including [2, 3, 5, 6, 7]. If X is a set, then |X| denotes the cardinality of X. For undefined terms in this paper, see [1,4].

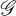THEOREM 1. Let I be an ideal of S, a subgroup of 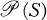. Then 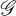has a normal subgroups 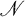such that 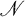is isomorphic to a subgroup of 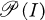and 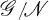is isomorphic to a subgroup of .

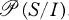Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 5 , 01 October 1979 , pp. 1077 - 1083
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Clifford, A. H. and Preston, G. B., The algebraic theory of semigroups, Vol. 1, Amer. Math. Soc. (Providence, Rhode Island, 1961).Google Scholar
2. McCarthy, D. J. and Hayes, D. L., Subgroups of the power semigroup of a group, J. of Comb. Theory, ser. A. 14 (1973), 173–186.Google Scholar
3. Putcha, M. S., On the maximal semilattice decomposition of the power semigroup of a semigroup, Semigroup Foru. 15 (1978), 263–267.Google Scholar
4. Rhodes, J. L. and Tilson, B. R., Local structure of finite semigroups, in “Algebraic Theory of Machines, Languages, and Semigroups,” M. A. Arbib, éd., Chapter 7 (Academic Press, 1968).Google Scholar
5. Tamura, T. and Shafer, J., Power semigroups, Math. Japan. 12 (1967), 25–32.Google Scholar
6. Tamura, T. and Shafer, J., Power semigroups II, Notices AMS, 15 (1968), 395.Google Scholar
7. Trnkova, V., On a representation of commutative semigroups, Semigroup Foru. 10 (1975), 203–214.Google Scholar