Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T01:11:14.287Z Has data issue: false hasContentIssue false
  • English
  • Français

The Strong ϕ Topology on Symmetric Sequence Spaces

Published online by Cambridge University Press:  20 November 2018

William H. Ruckle
William H. Ruckle*
Affiliation:
Clemson University, Clemson, South Carolina
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The strong ϕ topology. Let S be a linear space of real sequences written in functional notation

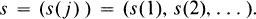
There is a natural duality between S and the space ϕ of sequences which are eventually ϕ given by the equation

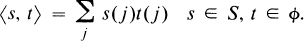
The series has only a finite number of nonzero terms since t is in ϕ.

A subset B of ϕ is called S-bounded if

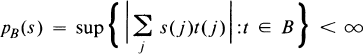
for each s in S.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 6 , 01 December 1985 , pp. 1112 - 1133
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Bourbaki, N., Eléments de mathématique, Livre V, Espaces vectouriels topologiques, 2 Vols. Act. Sci. et Ind. V 1189, 1229 (1953, 55).Google Scholar
2. Köthe, G., Topological vector spaces I Grundleheren d. Math. Wissen. 159 (Springer, New York, Berlin, Heidelberg, 1969).Google Scholar
3. Köthe, G. and Toeplitz, O., Lineare Raume mit unendlich vielen Koordinaten und Ringe unendlicher Matrizen, J. f. Math. 171 (1934), 193–226.Google Scholar
4. Garling, D. J. H., On symmetric sequence spaces, Proceedings of the London Math. Soc, (3) 76 (1966), 85–106.Google Scholar
5. Garling, D. J. H., Symmetric bases of locally convex spaces, Studia Mathematica 30 (1968), 164–181.Google Scholar
6. Garling, D. J. H., A class of reflexive symmetric BK-spaces, Can. J. Math. 21 (1969), 602–608.Google Scholar
7. Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces I, sequence spaces (Springer, Berlin, Heidelberg, New York, 1977).Google Scholar
8. Ruckle, W. H., Symmetric coordinate spaces and symmetric bases, Can. J. Math. 19 (1967), 828–838.Google Scholar
9. Ruckle, W. H., On perfect symmetric sequence spaces, Math. Annalen 175 (1968), 121–126.Google Scholar
10. Ruckle, W. H., FK-spaces in which the sequence of coordinate vectors is bounded, Can. J. Math. 25 (1973), 973–978.Google Scholar
11. Ruckle, W. H., Representation and series summability of complete biorthogonal sequences, Pacific J. Math. 34 (1910), 511–528.Google Scholar
12. Ruckle, W. H., Sequence spaces (London, Pitman, 1981).Google Scholar
13. Seever, G. L., Measures on F-spaces, Trans. A.M.S. 133 (1968), 267–280.Google Scholar
14. Singer, I., Bases in Banach spaces II (Springer, Berlin, Heidelberg, New York, 1981).CrossRefGoogle Scholar
15. Wilansky, A., Functional analysis (Blaisdell, New York, 1964).Google Scholar