Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T01:10:17.682Z Has data issue: false hasContentIssue false
  • English
  • Français

A Special Case of Completion Invariance for the c2 Invariant of a Graph

Published online by Cambridge University Press:  20 November 2018

Karen Yeats
Karen Yeats*
Affiliation:
Department of Combinatorics and Optimization, University of Waterloo, Waterloo, ON N2L 3G1, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The 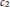${{c}_{2}}$ invariant is an arithmetic graph invariant defined by Schnetz. It is useful for understanding Feynman periods. Brown and Schnetz conjectured that the 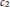${{c}_{2}}$ invariant has a particular symmetry known as completion invariance. This paper will prove completion invariance of the 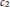${{c}_{2}}$ invariant in the case where we are over the field with 2 elements and the completed graph has an odd number of vertices. The methods involve enumerating certain edge bipartitions of graphs; two different constructions are needed.

Keywords

05C3105C3081T18c2 invariantFeynman graphedge partitionspanning forestcompletion conjecture
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 6 , 01 December 2018 , pp. 1416 - 1435
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Ax, J., Zeroes of polynomials over finite fields. Amer. J. Math. 86 (1964), 255–261. http://dx.doi.Org/10.2307/2373163Google Scholar
[2] Belkale, P. and Brosnan, P., Matroids, motives, and a conjecture of Kontsevich. Duke Math. J. 116 (2003), 147–188. http://dx.doi.org/10.1215/S0012-7094-03-11615-4Google Scholar
[3] Bloch, S., Esnault, H., and Kreimer, D., On motives associated to graph polynomials. Comm. Math. Phys. 267 (2006), 181–225. http://dx.doi.Org/10.1007/s00220-006-0040-2Google Scholar
[4] Broadhurst, D. and Schnetz, O., Algebraic geometry informs perturbative quantum field theory. In PoS, volume LL2014, page 078, 2014. arxiv:1 409.5570Google Scholar
[5] Broadhurst, D. J. and Kreimer, D., Knots and numbers in ϕ4 theory to 7 loops and beyond. Internat. J. Modern Phys. C 6 (1995), 519–524. http://dx.doi.Org/10.1142/S012918319500037XGoogle Scholar
[6] Brown, F., Feynman amplitudes, coaction principle, and cosmic Galois group. Commun. Number Theory Phys. 11 (2017), no. 3, 453–556. http://dx.doi.Org/10.4310/CNTP.2017.v11.n3.a1Google Scholar
[7] Brown, F., On the periods of some Feynman integrals. arxiv:0910.0114Google Scholar
[8] Brown, F. and Schnetz, O., A K3 in ϕ4. Duke Math J. 161 (2012), 1817–1862. http://dx.doi.org/10.1215/00127094-1644201Google Scholar
[9] Brown, F. and Schnetz, O., Modular forms in quantum field theory. Commun. Number Theory Phys. 7 (2013), 293–325. http://dx.doi.org/10.4310/CNTP.2013.v7.n2.a3Google Scholar
[10] Brown, F., Schnetz, O., and Yeats, K., Properties ofC2 invariants of Feynman graphs. Adv. Theor. Math. Phys. 18 (2014), 323–362. http://dx.doi.org/10.4310/ATMP.2014.v18.n2.a2Google Scholar
[11] Brown, F. and Yeats, K., Spanning forest polynomials and the transcendental weight of Feynman graphs. Comm. Math. Phys. 301 (2011), 357–382. http://dx.doi.org/10.1007/s00220-010-1145-1Google Scholar
[12] Chaiken, S., A combinatorial proof of the all minors matrix tree theorem. SIAM J. Alg. Disc. Meth. 3 (1982), 319–329. http://dx.doi.Org/10.1137/0603033Google Scholar
[13] Chorney, W. and Yeats, K., C2 invariants of recursive families of graphs. arxiv:1701.01208Google Scholar
[14] Crump, I., Graph Invariants with Connections to the Feynman Period in 4 Theory. PhD thesis, Simon Fraser University, 2017. arxiv:1704.06350Google Scholar
[15] Cummins, R. L., Hamilton circuits in tree graphs. IEEE Trans. Circuit Theory CT-13 (1966), 82–90. http://dx.doi.Org/1 0.1109/TCT.1 966.1082546Google Scholar
[16] Diestel, R., Graph theory. Graduate Texts in Mathematics, 173, Springer-Verlag, New York, 1997.Google Scholar
[17] Doryn, D., The C2 invariant is invariant. arxiv:1312.7271Google Scholar
[18] Doryn, D., Dual graph polynomials and a i-face formula. arxiv:1508.03484Google Scholar
[19] Itzykson, C. and Zuber, J.-B., Quantum field theory. International Series in Pure and Applied Physics, McGraw-Hill, 1980. Dover edition 2005.Google Scholar
[20] Logan, A., New realizations of modular forms in Calabi-Yau threefolds arising from ϕ4 theory. arxiv:1 604.0491 8Google Scholar
[21] Marcolli, M., Feynman motives. World Scientific, Hackensack, NJ, 2010.Google Scholar
[22] Schnetz, O., Numbers and functions in quantum field theory. arxiv:1606.08598Google Scholar
[23] Schnetz, O., Quantum periods: A census of ϕ4 -transcendentals. Commun. Number Theory Phys. 4 (2010), 1–47. http://dx.doi.org/10.4310/CNTP.2010.v4.n1 .a1Google Scholar
[24] Schnetz, O., Quantum field theory over Fq. Electron. J. Combin. 18 (2011), no. 1, Paper 102.Google Scholar
[25] Vlasev, A. and Yeats, K., A four-vertex, quadratic, spanning forest polynomial identity. Electron. J. Linear Algebra 23 (2012), 923–941. http://dx.doi.Org/10.13001/1081-3810.1566Google Scholar
[26] Yeats, K., A few c2 invariants of circulant graphs. Commun. Number Theory Phys. 10 (2016), 63–86. http://dx.doi.org/10.4310/CNTP.2016.v10.n1 .a3Google Scholar