Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-29T01:43:48.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Smooth Finite Dimensional Embeddings

Published online by Cambridge University Press:  20 November 2018

R. Mansfield ,
H. Movahedi-Lankarani  and
R. Wells
R. Mansfield
Affiliation:
Department of Mathematics, Penn State University, University Park, Pennsylvania 16802, U.S.A. email: [email protected]
H. Movahedi-Lankarani
Affiliation:
Department of Mathematics, Penn State Altoona, Altoona, Pennsylvania 16601-3760, U.S.A. email: [email protected]
R. Wells
Affiliation:
Department of Mathematics, Penn State University, University Park, Pennsylvania 16802, U.S.A. email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give necessary and sufficient conditions for a norm-compact subset of a Hilbert space to admit a 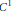${{C}^{1}}$ embedding into a finite dimensional Euclidean space. Using quasibundles, we prove a structure theorem saying that the stratum of $n$-dimensional points is contained in an $n$-dimensional 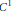${{C}^{1}}$ submanifold of the ambient Hilbert space. This work sharpens and extends earlier results of 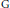$\text{G}$. Glaeser on paratingents. As byproducts we obtain smoothing theorems for compact subsets of Hilbert space and disjunction theorems for locally compact subsets of Euclidean space.

Keywords

57R9958A20tangent spacediffeomorphismmanifoldspherically compactparatingentquasibundleembedding
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 3 , 01 June 1999 , pp. 585 - 615
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Ben-Artzi, A., Eden, A., Foias, C. and Nicolaenko, B., Hölder continuity for the inverse of Mañé's projection. J. Math. Anal. Appl. 178 (1993), 22–29.Google Scholar
[2] Bouligand, G., Introduction à la géometrie infinitésimale direct. Vuibert, 1932.Google Scholar
[3] Bromberg, S., An extension theorem in class C1. Bol. Soc. Mat.Mexicana (2) 27 (1982), 35–44.Google Scholar
[4] Glaeser, G., Étude de quelques algèbres tayloriennes. J. Analyse Math. 6 (1958), 1–124. Erratum, insert to (2) 6 (1958).Google Scholar
[5] Federer, H., Geometric measure theory. Springer-Verlag, New York, 1969.Google Scholar
[6] Graham, G., Differentiable semigroups. Recent Developments in the Algebraic, Analytical, and Topological Theory of Semigroups (eds. Hofmann, K. H., J¨urgensen, H. and Weinert, H. J.), Lecture Notes in Math. 998, Springer, 1983, 57–127.Google Scholar
[7] Hirsch, M.W., Differential topology. Graduate Texts in Math. 33, Springer, New York, 1976.Google Scholar
[8] Hofmann, K. H. and Lawson, J. D., Foundations of Lie semigroups. Recent Developments in the Algebraic, Analytical, and Topological Theory of Semigroups (eds. Hofmann, K. H., J¨urgensen, H. and Weinert, H. J.), Lecture Notes in Math. 998, Springer, 1983, 128–201.Google Scholar
[9] Krivine, J. L., Introduction to axiomatic set theory. D. Reidel, 1971.Google Scholar
[10] Lashof, R. and Rothenberg, M., Microbundles and smoothing. Topology 3 (1965), 357–388.Google Scholar
[11] Luukkainen, J., Assouad dimension: antifractal metrization, porous sets, and homogeneous measures. J. Korean Math. Soc. 35 (1998), 23–76.Google Scholar
[12] Luukkainen, J. and Movahedi-Lankarani, H., Minimal bi-Lipschitz embedding dimension of ultrametric spaces. Fund. Math. 144 (1994), 181–193.Google Scholar
[13] Luukkainen, J. and Väisälä, J., Elements of Lipschitz Topology. Ann. Acad. Sci. Fenn. Ser. A I Math. 3 (1977), 85–122.Google Scholar
[14] Malgrange, B., Ideals of differentiable functions. Oxford University Press, Oxford, 1966.Google Scholar
[15] Mañé, R., On the dimension of the compact invariant sets of certain nonlinear maps. Lecture Notes in Math. 898, Springer-Verlag, New York, 1981, 230–240.Google Scholar
[16] Milnor, J., Lectures on differential topology. Princeton University, 1958.Google Scholar
[17] Milnor, J., Topology from a differential viewpoint. University of Virginia Press, 1965.Google Scholar
[18] Movahedi-Lankarani, H., Minimal Lipschitz embeddings. Ph.D. thesis, Pennsylvania State University, 1990.Google Scholar
[19] Movahedi-Lankarani, H., On the inverse of Mañé's projection. Proc. Amer.Math. Soc. 116 (1992), 555–560.Google Scholar
[20] Movahedi-Lankarani, H., On the theorem of Rademacher. Real Anal. Exchange (2) 17 (1992), 802–808.Google Scholar
[21] Movahedi-Lankarani, H. and Wells, R., The topology of quasibundles. Canad. J. Math. (6) 47 (1995), 1290–1316.Google Scholar
[22] Palais, R., Foundations of global non-linear analysis. W. A. Benjamin, Inc., New York, 1968.Google Scholar
[23] Repovˇs, D., Spokenkov, A. B. and Ščepin, E. V., C1-homogeneous compacta in Rn are C1-submanifolds of R n. Proc. Amer.Math. Soc. 124 (1996), 1219-1226.Google Scholar
[24] Samsonowicz, J., Images of vector bundles morphisms. Bull. Polish Acad. Sci. Math. 34 (1986), 599–607.Google Scholar
[25] Takens, F., On the numerical determination of the dimension of an attractor. Lecture Notes in Math. 1125, Springer-Verlag, New York, 1985, 99–106.Google Scholar
[26] Tremblay, P., The unstable manifold theorem: A proof for the common man.Master's thesis, Pennsylvania State University, 1988.Google Scholar
[27] Whitney, H., Analytic extensions of differentiable functions defined in closed sets. Trans. Amer. Math. Soc. 36 (1934), 63–89.Google Scholar