No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
Let 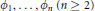 ${{\phi }_{1}},...,{{\phi }_{n}}\,(n\,\ge \,2)$ be nonzero integers such that the equation
${{\phi }_{1}},...,{{\phi }_{n}}\,(n\,\ge \,2)$ be nonzero integers such that the equation
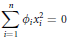 $$\sum\limits_{i=1}^{n}{{{\phi }_{i}}x_{i}^{2}\,=\,0}$$
$$\sum\limits_{i=1}^{n}{{{\phi }_{i}}x_{i}^{2}\,=\,0}$$
is solvable in integers 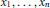 ${{x}_{1}},...,{{x}_{n}}$ not all zero. It is shown that there exists a solution satisfying
${{x}_{1}},...,{{x}_{n}}$ not all zero. It is shown that there exists a solution satisfying
,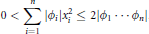 $$0\,<\,\sum\limits_{i}^{n}{\left| {{\phi }_{i}}\left| x_{i}^{2}\,\le \,2 \right|{{\phi }_{1}}...{{\phi }_{n}}\, \right|}$$
$$0\,<\,\sum\limits_{i}^{n}{\left| {{\phi }_{i}}\left| x_{i}^{2}\,\le \,2 \right|{{\phi }_{1}}...{{\phi }_{n}}\, \right|}$$
and that the constant 2 is best possible.