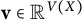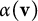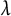1 Introduction
There is a surprising inverse correlation between the number of distinct eigenvalues of a graph and the size of its automorphism group. If the automorphism group of a graph G is arc-transitive, the graph has at most two simple eigenvalues. Conversely, if a connected graph on n vertices has at most two distinct eigenvalues, then the graph is complete and the automorphism group is the full symmetric group of n elements. We would like to study classes of graphs with many automorphisms and several simple eigenvalues, with the intuition that they should not be many in number and with the hope that we may describe them.
We consider a vertex-transitive graph X on n vertices and let A denote its adjacency matrix. We speak of eigenvalues and eigenvectors of A and of X interchangeably. There has been extensive study about the interplay of eigenvalues of a graph and various graph properties, such as the diameter [Reference Chung5, Reference Mohar18] or the chromatic number [Reference Haemers15, Reference Hoffman16] (see also [Reference Mohar and Poljak19]). The relationship between symmetries of a graph and its eigenvalues has also been investigated extensively, for example, in [Reference Chan and Godsil4, Reference Rowlinson27, Reference Rowlinson28].
In this paper, we focus on simple eigenvalues of cubic vertex-transitive graphs. If
![]() $\lambda $
is a simple eigenvalue of such a graph, it must be equal to
$\lambda $
is a simple eigenvalue of such a graph, it must be equal to
![]() $\pm 3$
or to
$\pm 3$
or to
![]() $\pm 1$
. Cubic vertex-transitive graphs have been studied extensively [Reference Potočnik, Spiga and Verret24, Reference Potočnik, Spiga and Verret25], and a census of all such graphs with at most 1,280 vertices is maintained by Potočnik, Spiga, and Verret in [Reference Potočnik, Spiga and Verret26].
$\pm 1$
. Cubic vertex-transitive graphs have been studied extensively [Reference Potočnik, Spiga and Verret24, Reference Potočnik, Spiga and Verret25], and a census of all such graphs with at most 1,280 vertices is maintained by Potočnik, Spiga, and Verret in [Reference Potočnik, Spiga and Verret26].
Using tools from diverse areas including topological graph theory, and algebraic number theory, we study the combinatorial structure of cubic, vertex-transitive graphs with
![]() $\lambda =1$
as a simple eigenvalue and give several families of graphs with such spectral property, and completely classify some of special subfamilies. Somewhat more generally, we classify all generalized Petersen graphs (which have one or two orbits under the automorphism group action) with simple eigenvalue 1. We also consider the possibility that
$\lambda =1$
as a simple eigenvalue and give several families of graphs with such spectral property, and completely classify some of special subfamilies. Somewhat more generally, we classify all generalized Petersen graphs (which have one or two orbits under the automorphism group action) with simple eigenvalue 1. We also consider the possibility that
![]() $-1$
and
$-1$
and
![]() $+1$
are both simple eigenvalues, and we prove that this happens only when the graph is bipartite.
$+1$
are both simple eigenvalues, and we prove that this happens only when the graph is bipartite.
For example, there are
![]() $85$
connected cubic graphs, up to isomorphism, on
$85$
connected cubic graphs, up to isomorphism, on
![]() $12$
vertices; of these,
$12$
vertices; of these,
![]() $21$
have
$21$
have
![]() $1$
as a simple eigenvalue. There is exactly one graph (up to isomorphism) on
$1$
as a simple eigenvalue. There is exactly one graph (up to isomorphism) on
![]() $12$
vertices, which is vertex-transitive, cubic, and has
$12$
vertices, which is vertex-transitive, cubic, and has
![]() $1$
as a simple eigenvalue, which is the prism graph on
$1$
as a simple eigenvalue, which is the prism graph on
![]() $12$
vertices, as shown in Figure 1. This graph has both
$12$
vertices, as shown in Figure 1. This graph has both
![]() $1$
and
$1$
and
![]() $-1$
as simple eigenvalues. The eigenvectors, depicted as assignments
$-1$
as simple eigenvalues. The eigenvectors, depicted as assignments
![]() $\pm 1$
to the vertices, are shown in Figure 1; we will see in Section 2, from a classical result of Petersdorf and Sachs [Reference Petersdorf and Sachs23], that any vertex-transitive graph has an eigenvector with entries in
$\pm 1$
to the vertices, are shown in Figure 1; we will see in Section 2, from a classical result of Petersdorf and Sachs [Reference Petersdorf and Sachs23], that any vertex-transitive graph has an eigenvector with entries in
![]() $\pm 1$
for each eigenvalue. Here, coloring a vertex with color
$\pm 1$
for each eigenvalue. Here, coloring a vertex with color
![]() $0$
if the eigenvectors for
$0$
if the eigenvectors for
![]() $1$
and
$1$
and
![]() $-1$
agree and with color
$-1$
agree and with color
![]() $1$
otherwise results in a proper
$1$
otherwise results in a proper
![]() $2$
-coloring of the graph; one of the color classes is shown by a dotted circle in the rightmost picture in Figure 1. We show that this holds in general, in Section 3.
$2$
-coloring of the graph; one of the color classes is shown by a dotted circle in the rightmost picture in Figure 1. We show that this holds in general, in Section 3.
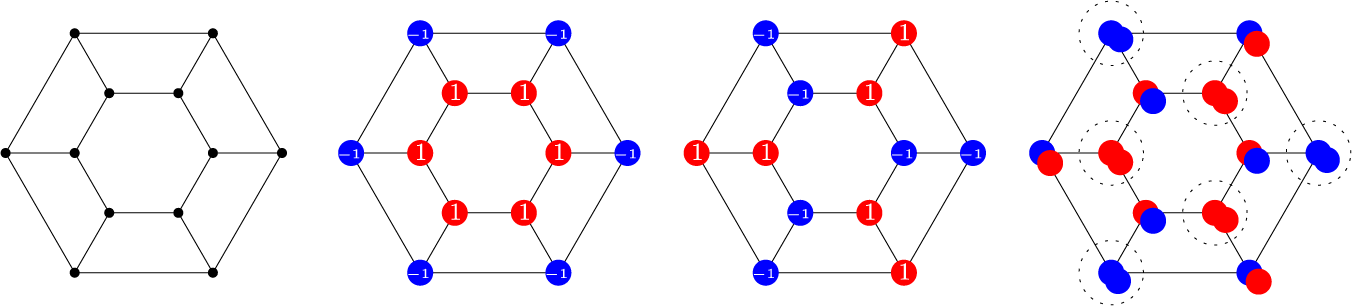
Figure 1: Eigenvectors for the prism graph of order
![]() $12$
. Left to right: the prism graph on
$12$
. Left to right: the prism graph on
![]() $12$
vertices, an eigenvector with eigenvalue
$12$
vertices, an eigenvector with eigenvalue
![]() $1$
, an eigenvector with eigenvalue
$1$
, an eigenvector with eigenvalue
![]() $-1$
, and the bipartite classes of the prism with classes determined by whether or not the eigenvectors agree or disagree at a vertex.
$-1$
, and the bipartite classes of the prism with classes determined by whether or not the eigenvectors agree or disagree at a vertex.
The organization of the paper is as follows. In Section 2, we give preliminaries regarding eigenvectors of simple eigenvalues. In Section 3, we use these to show the previously mentioned result that having both
![]() $1$
and
$1$
and
![]() $-1$
as simple eigenvalues implies that a cubic graph is bipartite. We continue to extract more information about the structure of the graph, as constrained by the eigenvector, in Section 4. In Section 5, we find a connection to regular maps; we show that the vertex deletion of a regular map gives a cubic vertex-transitive graph with
$-1$
as simple eigenvalues implies that a cubic graph is bipartite. We continue to extract more information about the structure of the graph, as constrained by the eigenvector, in Section 4. In Section 5, we find a connection to regular maps; we show that the vertex deletion of a regular map gives a cubic vertex-transitive graph with
![]() $1$
as a (not necessarily simple) eigenvalue. Finally, in Section 6, we give several infinite families of examples of cubic vertex-transitive graphs with
$1$
as a (not necessarily simple) eigenvalue. Finally, in Section 6, we give several infinite families of examples of cubic vertex-transitive graphs with
![]() $1$
as a simple eigenvalue; in each case, we find an infinite family of cubic vertex-transitive graph with
$1$
as a simple eigenvalue; in each case, we find an infinite family of cubic vertex-transitive graph with
![]() $1$
as an eigenvalue and then we classify when
$1$
as an eigenvalue and then we classify when
![]() $1$
occurs as a simple eigenvalue. In particular, we classify which generalized Petersen graphs have
$1$
occurs as a simple eigenvalue. In particular, we classify which generalized Petersen graphs have
![]() $1$
as a simple eigenvalue, using classical results in number theory about vanishing roots of unity and sums of cosines.
$1$
as a simple eigenvalue, using classical results in number theory about vanishing roots of unity and sums of cosines.
2 Partitions and eigenvectors
Consider a vertex-transitive graph X with vertex-set V, and let A denote its adjacency matrix. We index rows and columns of the adjacency matrix
![]() $A = A(X)$
of X by vertices of X. We will use functional notation where
$A = A(X)$
of X by vertices of X. We will use functional notation where
![]() $A(x,y)$
denotes the
$A(x,y)$
denotes the
![]() $(x,y)$
-entry of A. For a vector
$(x,y)$
-entry of A. For a vector
![]() ${\mathbf v}$
indexed by the vertices of X and a vertex x of X, we write
${\mathbf v}$
indexed by the vertices of X and a vertex x of X, we write
![]() ${\mathbf v}(x)$
for the entry of
${\mathbf v}(x)$
for the entry of
![]() ${\mathbf v}$
corresponding to x.
${\mathbf v}$
corresponding to x.
An eigenvalue of a graph X is simple if the corresponding eigenspace is one-dimensional. Let
![]() $\lambda $
be an eigenvalue of X with eigenvector
$\lambda $
be an eigenvalue of X with eigenvector
![]() ${\mathbf v}$
. The elements of the automorphism group of X, denoted
${\mathbf v}$
. The elements of the automorphism group of X, denoted
![]() $\operatorname {\mathrm {Aut}}(X)$
, can be represented by
$\operatorname {\mathrm {Aut}}(X)$
, can be represented by
![]() $V\times V$
permutation matrices P such that
$V\times V$
permutation matrices P such that
![]() $P^T A P = A$
. Note that
$P^T A P = A$
. Note that
![]() $P^T = P^{-1}$
.
$P^T = P^{-1}$
.
We may observe that if
![]() $A {\mathbf v} = \lambda {\mathbf v}$
and
$A {\mathbf v} = \lambda {\mathbf v}$
and
![]() ${\mathbf v} \neq 0$
, then
${\mathbf v} \neq 0$
, then
and thus
![]() $P{\mathbf v}$
is also an eigenvector of A with eigenvalue
$P{\mathbf v}$
is also an eigenvector of A with eigenvalue
![]() $\lambda $
. Therefore, any automorphism P of X fixes the eigenspaces of A.
$\lambda $
. Therefore, any automorphism P of X fixes the eigenspaces of A.
In particular, if
![]() $\lambda $
is a simple eigenvalue of X, then the eigenspace of
$\lambda $
is a simple eigenvalue of X, then the eigenspace of
![]() $\lambda $
has dimension 1 and so
$\lambda $
has dimension 1 and so
for some scalar
![]() $\gamma \in {\mathbb R}$
. Since P is a permutation matrix, we have
$\gamma \in {\mathbb R}$
. Since P is a permutation matrix, we have
![]() $\gamma \in \{1, -1\}$
. If P is an automorphism of X mapping vertex x to y, then
$\gamma \in \{1, -1\}$
. If P is an automorphism of X mapping vertex x to y, then
![]() ${\mathbf v}(x) = \pm {\mathbf v}(y)$
. Since X is vertex-transitive, for each pair of vertices
${\mathbf v}(x) = \pm {\mathbf v}(y)$
. Since X is vertex-transitive, for each pair of vertices
![]() $x,y$
, there exists an automorphism P mapping x to y. Therefore,
$x,y$
, there exists an automorphism P mapping x to y. Therefore,
![]() ${\mathbf v}$
has entries
${\mathbf v}$
has entries
![]() $\pm \beta $
for some
$\pm \beta $
for some
![]() $\beta \in {\mathbb R}$
. We may scale the eigenvector to obtain that
$\beta \in {\mathbb R}$
. We may scale the eigenvector to obtain that
![]() ${\mathbf v}$
is a
${\mathbf v}$
is a
![]() $\pm 1$
vector.
$\pm 1$
vector.
We have the following standard theorem, which can be found in [Reference Biggs2] or [Reference Cvetković, Doob and Sachs10].
Theorem 2.1 (Petersdorf and Sachs [Reference Petersdorf and Sachs23])
Let X be a vertex-transitive graph of degree k. If
![]() $\lambda $
is a simple eigenvalue of X, then
$\lambda $
is a simple eigenvalue of X, then
for some integer
![]() $\alpha \in \{0, \ldots , k\}$
.
$\alpha \in \{0, \ldots , k\}$
.
Proof Let
![]() $\lambda $
be a simple eigenvalue of X, and let
$\lambda $
be a simple eigenvalue of X, and let
![]() ${\mathbf v}$
be its
${\mathbf v}$
be its
![]() $\pm 1$
eigenvector. Let x be a vertex of X. Without loss of generality, we may assume
$\pm 1$
eigenvector. Let x be a vertex of X. Without loss of generality, we may assume
![]() ${\mathbf v}(x) = 1$
. We have that
${\mathbf v}(x) = 1$
. We have that
Let
![]() $\alpha \ (0\leq \alpha \leq k)$
be the number of neighbors y of x such that
$\alpha \ (0\leq \alpha \leq k)$
be the number of neighbors y of x such that
![]() ${\mathbf v}(y) = -1$
. Then (2.1) implies that
${\mathbf v}(y) = -1$
. Then (2.1) implies that
![]() $\lambda = k-2\alpha $
.
$\lambda = k-2\alpha $
.
This proof shows that X has a
![]() $\pm 1$
eigenvector whose signs determine a partition
$\pm 1$
eigenvector whose signs determine a partition
such that the induced subgraphs
![]() $X[V^+]$
and
$X[V^+]$
and
![]() $X[V^-]$
are
$X[V^-]$
are
![]() $(k-\alpha )$
-regular and the bipartite subgraph between
$(k-\alpha )$
-regular and the bipartite subgraph between
![]() $V^+$
and
$V^+$
and
![]() $V^-$
is
$V^-$
is
![]() $\alpha $
-regular. Conversely, every such partition determines a
$\alpha $
-regular. Conversely, every such partition determines a
![]() $\pm 1$
eigenvector of X for eigenvalue
$\pm 1$
eigenvector of X for eigenvalue
![]() $\lambda = k-2\alpha $
. We have the following observation.
$\lambda = k-2\alpha $
. We have the following observation.
Lemma 2.2 Let X be a connected k-regular graph with an eigenvector
![]() ${\mathbf v}$
for an eigenvalue
${\mathbf v}$
for an eigenvalue
![]() $\lambda $
, whose coordinates are all
$\lambda $
, whose coordinates are all
![]() $\pm 1$
. Then
$\pm 1$
. Then
![]() $\lambda $
is an integer and
$\lambda $
is an integer and
![]() $\lambda \equiv k \pmod 2$
. The sets
$\lambda \equiv k \pmod 2$
. The sets
![]() $V^+=\{x\in V(X)\mid {\mathbf v}(x)=1\}$
and
$V^+=\{x\in V(X)\mid {\mathbf v}(x)=1\}$
and
![]() $V^- = V(X)\setminus V^+$
induce
$V^- = V(X)\setminus V^+$
induce
![]() $\left (\frac {k+\lambda }{2}\right )$
-regular subgraphs, while the edges joining
$\left (\frac {k+\lambda }{2}\right )$
-regular subgraphs, while the edges joining
![]() $V^+$
and
$V^+$
and
![]() $V^-$
form a
$V^-$
form a
![]() $\left (\frac {k-\lambda }{2}\right )$
-regular bipartite subgraph of X. Conversely, every such partition determines a
$\left (\frac {k-\lambda }{2}\right )$
-regular bipartite subgraph of X. Conversely, every such partition determines a
![]() $\pm 1$
eigenvector for
$\pm 1$
eigenvector for
![]() $\lambda $
.
$\lambda $
.
Proof If
![]() $V^+=V(X)$
or
$V^+=V(X)$
or
![]() $V^-=V(X)$
, then
$V^-=V(X)$
, then
![]() $\lambda = k$
and there is nothing to prove. Otherwise, equation (2.1) gives the rest of the claims.
$\lambda = k$
and there is nothing to prove. Otherwise, equation (2.1) gives the rest of the claims.
3 Cubic vertex-transitive graphs having
 $1$
and
$1$
and
 $-1$
as simple eigenvalues
$-1$
as simple eigenvalues
A cubic graph X has largest eigenvalue equal to
![]() $3$
, which is simple if and only if X is connected. It is well known that if
$3$
, which is simple if and only if X is connected. It is well known that if
![]() $-3$
is also an eigenvalue of X and X is connected, then
$-3$
is also an eigenvalue of X and X is connected, then
![]() $-3$
is a simple eigenvalue and X is bipartite. By Theorem 2.1, the only possible simple eigenvalues of a cubic vertex-transitive graph besides
$-3$
is a simple eigenvalue and X is bipartite. By Theorem 2.1, the only possible simple eigenvalues of a cubic vertex-transitive graph besides
![]() $\pm 3 $
are
$\pm 3 $
are
![]() $\pm 1$
.
$\pm 1$
.
A partition
![]() $\{V_1, \ldots , V_m\}$
of the vertices of a graph X is said to be equitable if the subgraph of X induced by each
$\{V_1, \ldots , V_m\}$
of the vertices of a graph X is said to be equitable if the subgraph of X induced by each
![]() $V_i$
is regular and the bipartite subgraph of X induced by the edges from
$V_i$
is regular and the bipartite subgraph of X induced by the edges from
![]() $V_i$
to
$V_i$
to
![]() $V_j$
is semiregular, for each pair
$V_j$
is semiregular, for each pair
![]() $i,j$
such that
$i,j$
such that
![]() $i \neq j$
. If that is the case, then we define the
$i \neq j$
. If that is the case, then we define the
![]() $m\times m$
quotient matrix
$m\times m$
quotient matrix
![]() $B = [b_{ij}]_{i,j = 1}^m$
whose entries
$B = [b_{ij}]_{i,j = 1}^m$
whose entries
![]() $b_{ij}$
are number of neighbors of any vertex in
$b_{ij}$
are number of neighbors of any vertex in
![]() $V_i$
in
$V_i$
in
![]() $V_j$
.
$V_j$
.
Theorem 3.1 If a cubic vertex-transitive graph X has both
![]() $1$
and
$1$
and
![]() $-1$
as simple eigenvalues, then X is bipartite.
$-1$
as simple eigenvalues, then X is bipartite.
Proof Let
![]() ${\mathbf v}$
and
${\mathbf v}$
and
![]() ${\mathbf u}$
be the
${\mathbf u}$
be the
![]() $\pm 1$
eigenvectors for eigenvalues
$\pm 1$
eigenvectors for eigenvalues
![]() $1$
and
$1$
and
![]() $-1$
, respectively. Let
$-1$
, respectively. Let
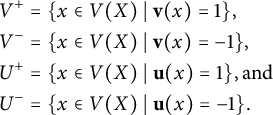 $$\begin{align*}\begin{aligned} V^+ &= \{x \in V(X) \mid {\mathbf v}(x) = 1\}, \\ V^- &= \{x \in V(X) \mid {\mathbf v}(x) = -1\}, \\ U^+ &= \{x \in V(X) \mid {\mathbf u}(x) = 1\}, \mbox{and} \\ U^- &= \{x \in V(X) \mid {\mathbf u}(x) = -1\}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} V^+ &= \{x \in V(X) \mid {\mathbf v}(x) = 1\}, \\ V^- &= \{x \in V(X) \mid {\mathbf v}(x) = -1\}, \\ U^+ &= \{x \in V(X) \mid {\mathbf u}(x) = 1\}, \mbox{and} \\ U^- &= \{x \in V(X) \mid {\mathbf u}(x) = -1\}. \end{aligned} \end{align*}$$
For any automorphism P in
![]() $\operatorname {\mathrm {Aut}}(X)$
, we have that P must either fix both
$\operatorname {\mathrm {Aut}}(X)$
, we have that P must either fix both
![]() $V^+$
and
$V^+$
and
![]() $V^-$
or interchange them as sets. Similarly, P either fixes both
$V^-$
or interchange them as sets. Similarly, P either fixes both
![]() $U^+$
and
$U^+$
and
![]() $U^-$
or interchanges them. By using (2.1), we see that
$U^-$
or interchanges them. By using (2.1), we see that
![]() $V^+$
and
$V^+$
and
![]() $V^-$
each induce a 2-regular subgraph of X and
$V^-$
each induce a 2-regular subgraph of X and
![]() $U^+$
and
$U^+$
and
![]() $U^-$
each induce a 1-regular subgraph of X.
$U^-$
each induce a 1-regular subgraph of X.
Let
![]() $W^{++} = V^+ \cap U^+ $
,
$W^{++} = V^+ \cap U^+ $
,
![]() $W^{+-} = V^+ \cap U^-$
,
$W^{+-} = V^+ \cap U^-$
,
![]() $W^{-+} = V^- \cap U^+ $
, and
$W^{-+} = V^- \cap U^+ $
, and
![]() $W^{--} = V^- \cap U^- $
. Consider the subgraph Y induced by the vertices in
$W^{--} = V^- \cap U^- $
. Consider the subgraph Y induced by the vertices in
![]() $W^{++}$
. Since
$W^{++}$
. Since
![]() $W^{++}\subseteq U^+$
, each vertex of
$W^{++}\subseteq U^+$
, each vertex of
![]() $W^{++}$
has degree 0 or 1 in Y. Since X is vertex-transitive, the automorphism group of X must also act transitively on Y. Then Y is either 1-regular (an induced matching) or an independent set of vertices. The same conclusion applies to
$W^{++}$
has degree 0 or 1 in Y. Since X is vertex-transitive, the automorphism group of X must also act transitively on Y. Then Y is either 1-regular (an induced matching) or an independent set of vertices. The same conclusion applies to
![]() $W^{+-}$
,
$W^{+-}$
,
![]() $W^{-+}$
, and
$W^{-+}$
, and
![]() $W^{--}$
.
$W^{--}$
.
If Y is 1-regular, then we easily conclude that the quotient matrix of the partition of
![]() $V(X)$
induced by
$V(X)$
induced by
![]() $W^{++}, W^{+-}, W^{-+}, W^{--}$
must be
$W^{++}, W^{+-}, W^{-+}, W^{--}$
must be
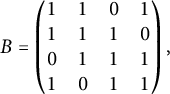 $$\begin{align*}B = \begin{pmatrix} 1 & 1 & 0 &1 \\ 1 & 1 & 1 & 0\\ 0 & 1 & 1 & 1\\ 1 & 0 & 1 & 1 \end{pmatrix}, \end{align*}$$
$$\begin{align*}B = \begin{pmatrix} 1 & 1 & 0 &1 \\ 1 & 1 & 1 & 0\\ 0 & 1 & 1 & 1\\ 1 & 0 & 1 & 1 \end{pmatrix}, \end{align*}$$
and this partition is equitable. By the interlacing theorem (see, e.g., [Reference Brouwer and Haemers3, Theorem 2.5.1]), the eigenvalues of B are a sub-multiset of the eigenvalues of A. The matrix B has eigenvalue
![]() $1$
with multiplicity 2 and so
$1$
with multiplicity 2 and so
![]() $A(X)$
also has eigenvalue 1 with multiplicity at least 2. This contradicts the assumption that 1 is a simple eigenvalue of X.
$A(X)$
also has eigenvalue 1 with multiplicity at least 2. This contradicts the assumption that 1 is a simple eigenvalue of X.
Therefore, it must be that
![]() $W^{++}$
is an independent set. In this case, by vertex transitivity, the same holds for
$W^{++}$
is an independent set. In this case, by vertex transitivity, the same holds for
![]() $ W^{+-}, W^{-+}$
, and
$ W^{+-}, W^{-+}$
, and
![]() $W^{--}$
. This implies that each vertex in
$W^{--}$
. This implies that each vertex in
![]() $W^{++}$
has two neighbors in
$W^{++}$
has two neighbors in
![]() $W^{+-}$
, one neighbor in
$W^{+-}$
, one neighbor in
![]() $W^{-+}$
, and no neighbors in
$W^{-+}$
, and no neighbors in
![]() $W^{++} \cup W^{--}$
. In particular, the partition of
$W^{++} \cup W^{--}$
. In particular, the partition of
![]() $V(X)$
into sets
$V(X)$
into sets
![]() $W^{++} \cup W^{--}$
and
$W^{++} \cup W^{--}$
and
![]() $W^{+-} \cup W^{-+}$
is a bipartition of the graph X.
$W^{+-} \cup W^{-+}$
is a bipartition of the graph X.
4 Combinatorial structure
We now consider a cubic vertex-transitive graph X that has
![]() $\lambda = 1$
as a simple eigenvalue with eigenvector
$\lambda = 1$
as a simple eigenvalue with eigenvector
![]() ${\mathbf v}$
whose entries are in
${\mathbf v}$
whose entries are in
![]() $\{1, -1\}$
. We define vertex sets
$\{1, -1\}$
. We define vertex sets
![]() $V^+$
and
$V^+$
and
![]() $V^-$
as in the previous section. In this section, we will extract more information about the combinatorial structure of
$V^-$
as in the previous section. In this section, we will extract more information about the combinatorial structure of
![]() $V^+$
and
$V^+$
and
![]() $V^-$
in the graph.
$V^-$
in the graph.
For
![]() $W \subseteq V(X)$
, we use
$W \subseteq V(X)$
, we use
![]() $X[W]$
to denote the subgraph of X induced by W. Let M denote the set of edges between
$X[W]$
to denote the subgraph of X induced by W. Let M denote the set of edges between
![]() $V^+$
and
$V^+$
and
![]() $V^-$
; that is,
$V^-$
; that is,
Lemma 4.1 For
![]() $(V^+, V^-)$
and M as defined above, the following statements are true:
$(V^+, V^-)$
and M as defined above, the following statements are true:
-
(i)
 $X[V^+]$
is the disjoint union of cycles of the same length;
$X[V^+]$
is the disjoint union of cycles of the same length; -
(ii)
 $X[V^+]$
is isomorphic to
$X[V^+]$
is isomorphic to
 $X[V^-]$
, and
$X[V^-]$
, and
 $V^+$
and
$V^+$
and
 $V^-$
are blocks of imprimitivity of the action of
$V^-$
are blocks of imprimitivity of the action of
 $\operatorname {\mathrm {Aut}}(X)$
;
$\operatorname {\mathrm {Aut}}(X)$
; -
(iii)
 $\bigl \{V^+, V^-\bigr \}$
is the unique partition of
$\bigl \{V^+, V^-\bigr \}$
is the unique partition of
 $V(X)$
, such that both parts induce 2-regular graphs;
$V(X)$
, such that both parts induce 2-regular graphs; -
(iv) M is a perfect matching of X; and
-
(v)
 $\operatorname {\mathrm {Aut}}(X)$
acts arc-transitively on M and fixes M setwise.
$\operatorname {\mathrm {Aut}}(X)$
acts arc-transitively on M and fixes M setwise.
Proof For every vertex
![]() $x\in V^+$
, we have that
$x\in V^+$
, we have that
![]() $\sum _{y\sim x} {\mathbf v}(y) = {\mathbf v}(x) = 1$
. Since
$\sum _{y\sim x} {\mathbf v}(y) = {\mathbf v}(x) = 1$
. Since
![]() ${\mathbf v}(y)$
for all y neighbors of x are either
${\mathbf v}(y)$
for all y neighbors of x are either
![]() $1$
or
$1$
or
![]() $-1$
, it follows that x is adjacent to two vertices in
$-1$
, it follows that x is adjacent to two vertices in
![]() $V^+$
and one vertex in
$V^+$
and one vertex in
![]() $V^-$
. This implies that M is a perfect matching of X and
$V^-$
. This implies that M is a perfect matching of X and
![]() $X[V^+]$
is a
$X[V^+]$
is a
![]() $2$
-regular graph.
$2$
-regular graph.
Any partition of
![]() $V(X)$
into sets
$V(X)$
into sets
![]() $(V_1, V_2)$
such that the induced graphs
$(V_1, V_2)$
such that the induced graphs
![]() $X[V_1]$
and
$X[V_1]$
and
![]() $X[V_2]$
are
$X[V_2]$
are
![]() $2$
-regular gives rise to an eigenvector for X with eigenvalue
$2$
-regular gives rise to an eigenvector for X with eigenvalue
![]() $1$
, by taking the vector
$1$
, by taking the vector
![]() ${\mathbf u}$
defined as follows:
${\mathbf u}$
defined as follows:
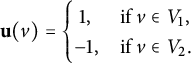 $$\begin{align*}{\mathbf u}(v) = \begin{cases} ~1, & \text{if } v \in V_1, \\ -1, & \text{if } v \in V_2. \end{cases} \end{align*}$$
$$\begin{align*}{\mathbf u}(v) = \begin{cases} ~1, & \text{if } v \in V_1, \\ -1, & \text{if } v \in V_2. \end{cases} \end{align*}$$
Since
![]() $1$
is a simple eigenvalue of X, it follows that
$1$
is a simple eigenvalue of X, it follows that
![]() $\{V^-, V^+\}$
is the only such partition. Then every automorphism of X must fix
$\{V^-, V^+\}$
is the only such partition. Then every automorphism of X must fix
![]() $V^+$
and
$V^+$
and
![]() $V^-$
or must swap
$V^-$
or must swap
![]() $V^+$
and
$V^+$
and
![]() $V^-$
setwise. This shows (v). Observe that there is an automorphism of X taking a vertex of
$V^-$
setwise. This shows (v). Observe that there is an automorphism of X taking a vertex of
![]() $V^+$
to a vertex in
$V^+$
to a vertex in
![]() $V^-$
. Such an automorphism must take every vertex in
$V^-$
. Such an automorphism must take every vertex in
![]() $V^+$
to a vertex in
$V^+$
to a vertex in
![]() $V^-$
and every vertex in
$V^-$
and every vertex in
![]() $V^-$
to a vertex in
$V^-$
to a vertex in
![]() $V^+$
and so is an isomorphism from
$V^+$
and so is an isomorphism from
![]() $X[V^+]$
to
$X[V^+]$
to
![]() $X[V^-]$
. This shows that (ii) holds. Since
$X[V^-]$
. This shows that (ii) holds. Since
![]() $\operatorname {\mathrm {Aut}}(X)$
acts transitively on X, the induced action on
$\operatorname {\mathrm {Aut}}(X)$
acts transitively on X, the induced action on
![]() $V^+$
is also transitive, so
$V^+$
is also transitive, so
![]() $X[V^+]$
is a vertex-transitive
$X[V^+]$
is a vertex-transitive
![]() $2$
-regular graph. Then
$2$
-regular graph. Then
![]() $X[V^+]$
must be a disjoint union of cycles of the same length.
$X[V^+]$
must be a disjoint union of cycles of the same length.
Lemma 4.1 motivates the question to classify cubic vertex-transitive graphs that admit a decomposition into a “bipartite” 2-factor and a perfect matching, where both factors are invariant under the full automorphism group. Inspired by this problem, Alspach, Khodadadpour, and Kreher [Reference Alspach, Khodadadpour and Kreher1] classified all cubic vertex-transitive graphs containing a Hamilton cycle that is invariant under the action of the automorphism group. In Section 6, we classify the cases when
![]() $G[V^+]$
is a single cycle and when the cycles in
$G[V^+]$
is a single cycle and when the cycles in
![]() $G[V^+]$
are triangles, respectively.
$G[V^+]$
are triangles, respectively.
We may assume that each of
![]() $X[V^+]$
and
$X[V^+]$
and
![]() $X[V^-]$
is the disjoint union of m cycles of length k. In this case, we say that X is of type
$X[V^-]$
is the disjoint union of m cycles of length k. In this case, we say that X is of type
![]() $C(m,k)$
.
$C(m,k)$
.
Let
![]() $C_i$
and
$C_i$
and
![]() $D_i \ (i = 1, \ldots , m)$
be the cycles forming
$D_i \ (i = 1, \ldots , m)$
be the cycles forming
![]() $X[V^+]$
and
$X[V^+]$
and
![]() $X[V^-]$
, respectively, as observed above. Let G be the multigraph obtained from X by contracting each cycle
$X[V^-]$
, respectively, as observed above. Let G be the multigraph obtained from X by contracting each cycle
![]() $C_i$
and each cycle
$C_i$
and each cycle
![]() $D_i$
to a single vertex. More precisely, G has
$D_i$
to a single vertex. More precisely, G has
![]() $2m$
vertices
$2m$
vertices
![]() $c_1,\dots ,c_m$
and
$c_1,\dots ,c_m$
and
![]() $d_1,\dots ,d_m$
(one for each cycle
$d_1,\dots ,d_m$
(one for each cycle
![]() $C_i$
or
$C_i$
or
![]() $D_i$
); there is an edge joining
$D_i$
); there is an edge joining
![]() $c_i$
and
$c_i$
and
![]() $d_r$
in G for each edge of X joining a vertex in
$d_r$
in G for each edge of X joining a vertex in
![]() $C_i$
to a vertex in
$C_i$
to a vertex in
![]() $D_r$
. We say that G is the contracted multigraph of X. Observe that G is a k-regular connected graph.
$D_r$
. We say that G is the contracted multigraph of X. Observe that G is a k-regular connected graph.
Lemma 4.2 If G is the contracted multigraph of X, then
![]() $\operatorname {\mathrm {Aut}}(X) \leq \operatorname {\mathrm {Aut}}(G)$
and any vertex-transitive subgroup of
$\operatorname {\mathrm {Aut}}(X) \leq \operatorname {\mathrm {Aut}}(G)$
and any vertex-transitive subgroup of
![]() $\operatorname {\mathrm {Aut}}(X)$
acts transitively on the arcs of G. In particular, G is arc-transitive and bipartite.
$\operatorname {\mathrm {Aut}}(X)$
acts transitively on the arcs of G. In particular, G is arc-transitive and bipartite.
Proof Consider any
![]() $\alpha \in \operatorname {\mathrm {Aut}}(X)$
. If we take the contracted multigraph of
$\alpha \in \operatorname {\mathrm {Aut}}(X)$
. If we take the contracted multigraph of
![]() $\alpha (X)$
, we again obtain G, since the cycles
$\alpha (X)$
, we again obtain G, since the cycles
![]() $C_i, D_j$
form blocks of imprimitivity under the action of
$C_i, D_j$
form blocks of imprimitivity under the action of
![]() $\operatorname {\mathrm {Aut}}(X)$
. Thus,
$\operatorname {\mathrm {Aut}}(X)$
. Thus,
![]() $\alpha $
acts on G as an automorphism, and so
$\alpha $
acts on G as an automorphism, and so
![]() $\operatorname {\mathrm {Aut}}(X) \leq \operatorname {\mathrm {Aut}}(G)$
. Let
$\operatorname {\mathrm {Aut}}(X) \leq \operatorname {\mathrm {Aut}}(G)$
. Let
![]() $\Gamma \leq \operatorname {\mathrm {Aut}}(X)$
act transitively on the vertices of X. Then
$\Gamma \leq \operatorname {\mathrm {Aut}}(X)$
act transitively on the vertices of X. Then
![]() $\Gamma $
acts arc-transitively on the edges of M, which are in one-to-one correspondence with the edges of G, and thus acts arc-transitively on G. Clearly, every edge in G connects some
$\Gamma $
acts arc-transitively on the edges of M, which are in one-to-one correspondence with the edges of G, and thus acts arc-transitively on G. Clearly, every edge in G connects some
![]() $c_i$
to some
$c_i$
to some
![]() $d_j$
, so G is bipartite.
$d_j$
, so G is bipartite.
5 Relation to regular maps
In this section, we explore the relation between the combinatorial structure given by the eigenvector of
![]() $1$
, as a simple eigenvalue, in a cubic vertex-transitive graph and the combinatorial structure of graph embeddings with a high degree of symmetry. In this setting, we can obtain from a regular map a cubic vertex-transitive graph with
$1$
, as a simple eigenvalue, in a cubic vertex-transitive graph and the combinatorial structure of graph embeddings with a high degree of symmetry. In this setting, we can obtain from a regular map a cubic vertex-transitive graph with
![]() $1$
as an eigenvalue.
$1$
as an eigenvalue.
First, we proceed with some preliminary definitions from the area of graph embeddings. Further details may be found in [Reference Mohar and Thomassen21] or [Reference Gross and Tucker13]. Let G be a connected multigraph. For each
![]() $v \in V(G)$
, let
$v \in V(G)$
, let
![]() $\pi _v$
be a cyclic permutation of the edges incident to v. Then
$\pi _v$
be a cyclic permutation of the edges incident to v. Then
![]() $\Pi = \{\pi _v \mid v\in V(G)\}$
is said to be a rotation system for G and
$\Pi = \{\pi _v \mid v\in V(G)\}$
is said to be a rotation system for G and
![]() $\pi _v$
is the local rotation at v. An automorphism
$\pi _v$
is the local rotation at v. An automorphism
![]() $\alpha $
of G is said to preserve the rotation system
$\alpha $
of G is said to preserve the rotation system
![]() $\Pi $
if it maps the local rotation
$\Pi $
if it maps the local rotation
![]() $\pi _v$
around each vertex v onto the local rotation
$\pi _v$
around each vertex v onto the local rotation
![]() $\pi _{\alpha (v)}$
of
$\pi _{\alpha (v)}$
of
![]() $\alpha (v)$
. More precisely, if
$\alpha (v)$
. More precisely, if
![]() $\pi _v = (e_1,e_2,\ldots , e_d)$
is the local rotation at v, then
$\pi _v = (e_1,e_2,\ldots , e_d)$
is the local rotation at v, then
![]() $\pi _{\alpha (v)} = (\alpha (e_1),\alpha (e_2), \ldots , \alpha (e_d))$
. The subgroup of
$\pi _{\alpha (v)} = (\alpha (e_1),\alpha (e_2), \ldots , \alpha (e_d))$
. The subgroup of
![]() $\operatorname {\mathrm {Aut}}(X)$
that preserves the rotation system
$\operatorname {\mathrm {Aut}}(X)$
that preserves the rotation system
![]() $\Pi $
is called the automorphism group of the graph with rotation system, and is denoted by
$\Pi $
is called the automorphism group of the graph with rotation system, and is denoted by
![]() $\operatorname {\mathrm {Aut}}(G,\Pi )$
.
$\operatorname {\mathrm {Aut}}(G,\Pi )$
.
Each rotation system of a graph describes a
![]() $2$
-cell embedding of G on an orientable surface: it defines a collection of closed walks, called facial walks or faces, such that each edge is traversed once in each direction by these walks, and by pasting disks onto each facial walk, we obtain a map, i.e., an orientable surface in which G is 2-cell embedded. Thus, we view the pair
$2$
-cell embedding of G on an orientable surface: it defines a collection of closed walks, called facial walks or faces, such that each edge is traversed once in each direction by these walks, and by pasting disks onto each facial walk, we obtain a map, i.e., an orientable surface in which G is 2-cell embedded. Thus, we view the pair
![]() $(G,\Pi )$
as a map, and we call
$(G,\Pi )$
as a map, and we call
![]() $\operatorname {\mathrm {Aut}}(G,\Pi )$
the group of map automorphisms corresponding to the map determined by the rotation system
$\operatorname {\mathrm {Aut}}(G,\Pi )$
the group of map automorphisms corresponding to the map determined by the rotation system
![]() $\Pi $
. A map is said to be orientably regular (or rotary [Reference Wilson29]) if
$\Pi $
. A map is said to be orientably regular (or rotary [Reference Wilson29]) if
![]() $\operatorname {\mathrm {Aut}}(G,\Pi )$
acts transitively on the arcs of G.
$\operatorname {\mathrm {Aut}}(G,\Pi )$
acts transitively on the arcs of G.
Let X be a cubic graph of type
![]() $C(m,k)$
. Suppose that
$C(m,k)$
. Suppose that
![]() $\Gamma $
is a subgroup of
$\Gamma $
is a subgroup of
![]() $\operatorname {\mathrm {Aut}}(X)$
that acts transitively on
$\operatorname {\mathrm {Aut}}(X)$
that acts transitively on
![]() $V(X)$
. Recall that
$V(X)$
. Recall that
![]() $V^+$
and
$V^+$
and
![]() $V^-$
are blocks of imprimitivity of
$V^-$
are blocks of imprimitivity of
![]() $\operatorname {\mathrm {Aut}}(X)$
and hence also of
$\operatorname {\mathrm {Aut}}(X)$
and hence also of
![]() $\Gamma $
. Similarly, the cycles
$\Gamma $
. Similarly, the cycles
![]() $C_1,\dots ,C_m$
and
$C_1,\dots ,C_m$
and
![]() $D_1,\dots ,D_m$
form a system of blocks of imprimitivity. The stabilizer of
$D_1,\dots ,D_m$
form a system of blocks of imprimitivity. The stabilizer of
![]() $C_1$
in
$C_1$
in
![]() $\Gamma $
(the subgroup of all elements of
$\Gamma $
(the subgroup of all elements of
![]() $\Gamma $
that fix
$\Gamma $
that fix
![]() $C_1$
) acts on the cycle
$C_1$
) acts on the cycle
![]() $C_1$
either as a cyclic group or as a dihedral group. In this section, we shall assume that the action is regular:
$C_1$
either as a cyclic group or as a dihedral group. In this section, we shall assume that the action is regular:
-
(A1) The stabilizer of
 $C_1$
in
$C_1$
in
 $\Gamma $
acts regularly on
$\Gamma $
acts regularly on
 $C_1$
.
$C_1$
.
Note that (A1) implies that the stabilizer of
![]() $C_1$
in
$C_1$
in
![]() $\Gamma $
preserves the orientation of
$\Gamma $
preserves the orientation of
![]() $C_1$
and acts on
$C_1$
and acts on
![]() $C_1$
regularly as the cyclic group
$C_1$
regularly as the cyclic group
![]() ${\mathbb Z}_k$
.
${\mathbb Z}_k$
.
Let
![]() $C_1=v_1v_2\dots v_k$
. Suppose that
$C_1=v_1v_2\dots v_k$
. Suppose that
![]() $D_1=w_1w_2\dots w_k$
is chosen so that
$D_1=w_1w_2\dots w_k$
is chosen so that
![]() $v_1w_1\in E(X)$
. For
$v_1w_1\in E(X)$
. For
![]() $i=1,\dots , m$
, let
$i=1,\dots , m$
, let
![]() $\gamma _i\in \Gamma $
be an automorphism that maps
$\gamma _i\in \Gamma $
be an automorphism that maps
![]() $C_1$
to
$C_1$
to
![]() $C_i$
, and let
$C_i$
, and let
![]() $\delta _i\in \Gamma $
be an automorphism that maps
$\delta _i\in \Gamma $
be an automorphism that maps
![]() $C_1$
to
$C_1$
to
![]() $D_i$
. Moreover, we may assume that
$D_i$
. Moreover, we may assume that
![]() $\gamma _1$
rotates
$\gamma _1$
rotates
![]() $C_1$
clockwise by one vertex, i.e.,
$C_1$
clockwise by one vertex, i.e.,
![]() $\gamma _0(v_j)=v_{j+1}$
for
$\gamma _0(v_j)=v_{j+1}$
for
![]() $j=1,\dots ,k$
(indices taken modulo k) and that
$j=1,\dots ,k$
(indices taken modulo k) and that
![]() $\delta _1$
maps
$\delta _1$
maps
![]() $v_j$
to
$v_j$
to
![]() $w_j$
for
$w_j$
for
![]() $j=1,\dots ,k$
.
$j=1,\dots ,k$
.
Theorem 5.1 If
![]() $\Gamma $
satisfies
$\Gamma $
satisfies
![]() $(\mathbf{A1})$
, then
$(\mathbf{A1})$
, then
![]() $\Gamma $
acts regularly on
$\Gamma $
acts regularly on
![]() $V(X)$
and hence X is a Cayley graph of the group generated by
$V(X)$
and hence X is a Cayley graph of the group generated by
![]() $\gamma _1$
and the involution
$\gamma _1$
and the involution
![]() $\delta _1$
.
$\delta _1$
.
Proof The group
![]() $\Gamma $
acts transitively on
$\Gamma $
acts transitively on
![]() $V(X)$
. To see that it is a Cayley graph, it suffices to show that its action is regular (no fixed points). So, suppose that
$V(X)$
. To see that it is a Cayley graph, it suffices to show that its action is regular (no fixed points). So, suppose that
![]() $\gamma \in \Gamma $
fixes a vertex v. Let
$\gamma \in \Gamma $
fixes a vertex v. Let
![]() $\alpha _v\in \Gamma $
be a group element that maps
$\alpha _v\in \Gamma $
be a group element that maps
![]() $v_1$
to v. Then
$v_1$
to v. Then
![]() $\alpha _v^{-1}\gamma \alpha _v$
fixes
$\alpha _v^{-1}\gamma \alpha _v$
fixes
![]() $v_1$
, and by (A1), it must be the identity automorphism. This implies that
$v_1$
, and by (A1), it must be the identity automorphism. This implies that
![]() $\gamma $
is the identity. This conclusion confirms the claim.
$\gamma $
is the identity. This conclusion confirms the claim.
Theorem 5.2 If
![]() $\Gamma $
satisfies
$\Gamma $
satisfies
![]() $(\mathbf{A1})$
, then the contracted multigraph G of X admits a rotation system
$(\mathbf{A1})$
, then the contracted multigraph G of X admits a rotation system
![]() $\Pi $
such that
$\Pi $
such that
![]() $\Gamma \le \operatorname {\mathrm {Aut}}(G,\Pi )$
. The group
$\Gamma \le \operatorname {\mathrm {Aut}}(G,\Pi )$
. The group
![]() $\Gamma $
acts arc-transitively on
$\Gamma $
acts arc-transitively on
![]() $(G,\Pi )$
and therefore
$(G,\Pi )$
and therefore
![]() $(G,\Pi )$
is an orientably regular map.
$(G,\Pi )$
is an orientably regular map.
Proof Fix an orientation of
![]() $C_1$
and orient each
$C_1$
and orient each
![]() $C_i$
and
$C_i$
and
![]() $D_i$
according to the orientation induced by
$D_i$
according to the orientation induced by
![]() $\gamma _i(C_1)$
and
$\gamma _i(C_1)$
and
![]() $\delta _i(C_1)$
, respectively. We claim that for each
$\delta _i(C_1)$
, respectively. We claim that for each
![]() $\gamma \in \Gamma $
, the orientation of the cycle
$\gamma \in \Gamma $
, the orientation of the cycle
![]() $\gamma (C_1)$
is preserved; that is, if
$\gamma (C_1)$
is preserved; that is, if
![]() $e = uv$
is oriented as
$e = uv$
is oriented as
![]() $uv$
in
$uv$
in
![]() $C_1$
, then the edge
$C_1$
, then the edge
![]() $\{\phi (u),\phi (v)\}$
is also oriented as
$\{\phi (u),\phi (v)\}$
is also oriented as
![]() $\phi (u)\phi (v)$
. Let us give the argument for the case when
$\phi (u)\phi (v)$
. Let us give the argument for the case when
![]() $\gamma (C_1) = D_i = \delta _i(C_1)$
. In that case,
$\gamma (C_1) = D_i = \delta _i(C_1)$
. In that case,
![]() $\delta _i^{-1} \gamma (C_1)$
fixes
$\delta _i^{-1} \gamma (C_1)$
fixes
![]() $C_1$
and hence by (A1) fixes the orientation of
$C_1$
and hence by (A1) fixes the orientation of
![]() $C_1$
. This implies that
$C_1$
. This implies that
![]() $\gamma $
and
$\gamma $
and
![]() $\delta _i$
must induce the same orientation on
$\delta _i$
must induce the same orientation on
![]() $D_i$
, which we were to prove.
$D_i$
, which we were to prove.
The orientations of cycles determine a rotation system on the contracted multigraph G of X, and as shown above,
![]() $\Gamma $
preserves the rotation around the vertex corresponding to
$\Gamma $
preserves the rotation around the vertex corresponding to
![]() $C_1$
. Suppose that there is
$C_1$
. Suppose that there is
![]() $\gamma \in \Gamma $
that does not preserve one of the rotations, say it maps the rotation around
$\gamma \in \Gamma $
that does not preserve one of the rotations, say it maps the rotation around
![]() $C_i$
onto the opposite rotation around
$C_i$
onto the opposite rotation around
![]() $D_j$
. (The proof of other cases is similar.) In that case,
$D_j$
. (The proof of other cases is similar.) In that case,
![]() $\gamma \gamma _i$
maps
$\gamma \gamma _i$
maps
![]() $C_1$
onto
$C_1$
onto
![]() $D_j$
with the opposite rotation as
$D_j$
with the opposite rotation as
![]() $\delta _j$
, which contradicts what we have proved above. This completes the proof.
$\delta _j$
, which contradicts what we have proved above. This completes the proof.
A special case when
![]() $m=1$
gives rise to regular embeddings of the two-vertex contracted multigraph (with k parallel edges). This case will be treated in a somewhat greater generality in Section 6.3.
$m=1$
gives rise to regular embeddings of the two-vertex contracted multigraph (with k parallel edges). This case will be treated in a somewhat greater generality in Section 6.3.
Given a graph embedding
![]() $(G,\Pi )$
, we define the vertex truncation of
$(G,\Pi )$
, we define the vertex truncation of
![]() $(G,\Pi )$
, denoted
$(G,\Pi )$
, denoted
![]() $T(G,\Pi )$
as follows: the vertices of
$T(G,\Pi )$
as follows: the vertices of
![]() $T(G,\Pi )$
are all incident pairs
$T(G,\Pi )$
are all incident pairs
![]() $(v,e)$
for
$(v,e)$
for
![]() $v \in V(G)$
and
$v \in V(G)$
and
![]() $e \in E(G)$
such that v is incident to e. Two vertices of
$e \in E(G)$
such that v is incident to e. Two vertices of
![]() $T(G,\Pi )$
, say
$T(G,\Pi )$
, say
![]() $(v,e)$
and
$(v,e)$
and
![]() $(w,f)$
, are adjacent if
$(w,f)$
, are adjacent if
![]() $e=f$
or if
$e=f$
or if
![]() $v = w$
and
$v = w$
and
![]() $\pi _v(e) = f$
. Roughly speaking, we obtain
$\pi _v(e) = f$
. Roughly speaking, we obtain
![]() $T(G,\Pi )$
from G by replacing each vertex of G with a cycle determined by
$T(G,\Pi )$
from G by replacing each vertex of G with a cycle determined by
![]() $\Pi $
. Figure 2 shows an example of a vertex truncation; on the left side of the figure, we have the complete graph
$\Pi $
. Figure 2 shows an example of a vertex truncation; on the left side of the figure, we have the complete graph
![]() $K_5$
embedded in the torus as a regular map, and on the right, we have the vertex truncation of this embedding.
$K_5$
embedded in the torus as a regular map, and on the right, we have the vertex truncation of this embedding.
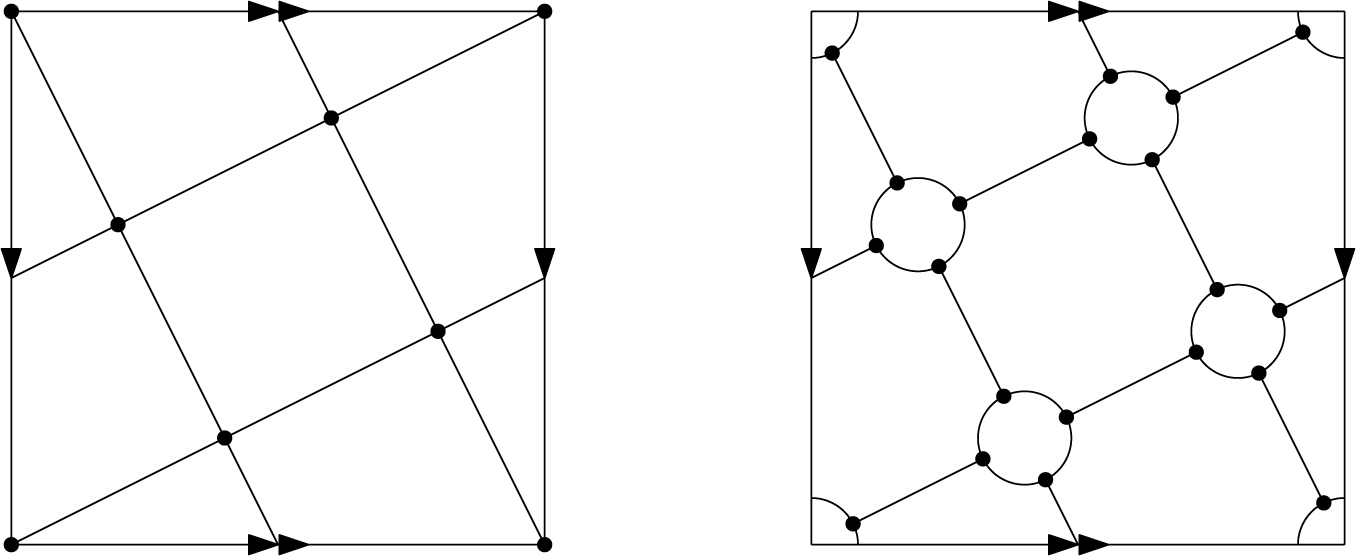
Figure 2: An example of a regular map (left) and its vertex truncation (right).
Lemma 5.3 If G is a bipartite, arc-transitive graph and
![]() $(G, \Pi )$
is an embedding of G on some orientable surface, then the vertex truncation
$(G, \Pi )$
is an embedding of G on some orientable surface, then the vertex truncation
![]() $T(G,\Pi )$
is a vertex-transitive cubic which has
$T(G,\Pi )$
is a vertex-transitive cubic which has
![]() $1$
as an eigenvalue.
$1$
as an eigenvalue.
Proof Each vertex
![]() $(v,e)$
of
$(v,e)$
of
![]() $T(G,\Pi )$
is adjacent to exactly three vertices:
$T(G,\Pi )$
is adjacent to exactly three vertices:
![]() $(v, \pi _v(e))$
,
$(v, \pi _v(e))$
,
![]() $(v, \pi _v^{-1}(e))$
, and
$(v, \pi _v^{-1}(e))$
, and
![]() $(w, e)$
, where
$(w, e)$
, where
![]() $e =vw$
. Since G is an arc-transitive graph, the automorphism group also acts transitively on the vertices of
$e =vw$
. Since G is an arc-transitive graph, the automorphism group also acts transitively on the vertices of
![]() $T(G, \Pi )$
, preserving adjacencies in
$T(G, \Pi )$
, preserving adjacencies in
![]() $T(G, \Pi )$
. Thus,
$T(G, \Pi )$
. Thus,
![]() $T(G, \Pi )$
is a cubic vertex-transitive graph.
$T(G, \Pi )$
is a cubic vertex-transitive graph.
Let
![]() $(A,B)$
be the bipartition of G. We will partition the vertices of
$(A,B)$
be the bipartition of G. We will partition the vertices of
![]() $T(G, \Pi )$
into
$T(G, \Pi )$
into
![]() $A' \cup B'$
as follows: let
$A' \cup B'$
as follows: let
We note that each vertex
![]() $(v,e=vw)$
of
$(v,e=vw)$
of
![]() $A'$
has two neighbors,
$A'$
has two neighbors,
![]() $(v, \pi _v(e))$
and
$(v, \pi _v(e))$
and
![]() $(v, \pi _v^{-1}(e))$
, in
$(v, \pi _v^{-1}(e))$
, in
![]() $A'$
and one neighbor
$A'$
and one neighbor
![]() $(w, e)$
in
$(w, e)$
in
![]() $B'$
. Similarly, each vertex of
$B'$
. Similarly, each vertex of
![]() $B'$
has two neighbors in
$B'$
has two neighbors in
![]() $B'$
and one neighbor in
$B'$
and one neighbor in
![]() $A'$
. Thus, the vector which takes value
$A'$
. Thus, the vector which takes value
![]() $1$
for each vertex of
$1$
for each vertex of
![]() $A'$
and value
$A'$
and value
![]() $-1$
for each vertex of
$-1$
for each vertex of
![]() $B'$
will be an eigenvector for
$B'$
will be an eigenvector for
![]() $A(T(G,\Pi ))$
with eigenvalue
$A(T(G,\Pi ))$
with eigenvalue
![]() $1$
.
$1$
.
We note that the vertex truncation of a bipartite arc-transitive graph does not necessarily have
![]() $1$
as a simple eigenvalue, but such graphs are good candidates for having
$1$
as a simple eigenvalue, but such graphs are good candidates for having
![]() $1$
as a simple eigenvalue because they have a
$1$
as a simple eigenvalue because they have a
![]() $\pm 1$
eigenvector for eigenvalue
$\pm 1$
eigenvector for eigenvalue
![]() $1$
, like the vertex-transitive cubic graphs with
$1$
, like the vertex-transitive cubic graphs with
![]() $1$
as a simple eigenvalue. The example in Figure 2 does not have
$1$
as a simple eigenvalue. The example in Figure 2 does not have
![]() $1$
as a simple eigenvalue. We note that if a graph embedding
$1$
as a simple eigenvalue. We note that if a graph embedding
![]() $(G,\Pi )$
is a regular map, then G is arc-transitive.
$(G,\Pi )$
is a regular map, then G is arc-transitive.
In Appendix B, we construct the vertex truncations of small regular maps from the census of Conder [Reference Conder6, Reference Conder7] and check when
![]() $1$
is indeed a simple eigenvalue. For example, the Möbius–Kantor graph has an embedding in the double torus which is a regular map; this embedding has with six octagonal faces and the full automorphism group, whose order is
$1$
is indeed a simple eigenvalue. For example, the Möbius–Kantor graph has an embedding in the double torus which is a regular map; this embedding has with six octagonal faces and the full automorphism group, whose order is
![]() $96$
, of the graph can be realized as the automorphism group of the map [Reference Coxeter9]. We computed that the vertex truncation of this embedding of the Möbius–Kantor graph has
$96$
, of the graph can be realized as the automorphism group of the map [Reference Coxeter9]. We computed that the vertex truncation of this embedding of the Möbius–Kantor graph has
![]() $1$
as a simple eigenvalue (see Table B.1).
$1$
as a simple eigenvalue (see Table B.1).
6 Families of graphs
In this section, we show the existence of several infinite families of cubic vertex-transitive graphs with
![]() $1$
as a simple eigenvalue. While it is not difficult to find infinite families of such graphs with
$1$
as a simple eigenvalue. While it is not difficult to find infinite families of such graphs with
![]() $1$
as an eigenvalue, it is often difficult to determine that
$1$
as an eigenvalue, it is often difficult to determine that
![]() $1$
is a simple eigenvalue. For these families, we have the characterization of when
$1$
is a simple eigenvalue. For these families, we have the characterization of when
![]() $1$
is simple, using some number-theoretic methods, as well as results about the sum of cosine, resulting from vanishing sums of roots of unity.
$1$
is simple, using some number-theoretic methods, as well as results about the sum of cosine, resulting from vanishing sums of roots of unity.
6.1 Cubic multigraphs (type
 $C(m,2)$
)
$C(m,2)$
)
Let X is a cubic vertex-transitive graph with
![]() $1$
as a simple eigenvalue. We first discuss the case when X contains multiple edges. When there is a triple edge, we have a two-vertex graph, denoted
$1$
as a simple eigenvalue. We first discuss the case when X contains multiple edges. When there is a triple edge, we have a two-vertex graph, denoted
![]() $K_2^3$
in Figure 3, whose eigenvalues are
$K_2^3$
in Figure 3, whose eigenvalues are
![]() $\pm 3$
. Otherwise, there are only double edges and single edges. Since X is vertex-transitive, every vertex x has two neighbors, one is joined to x by a double edge, the other one by a single edge. It follows that X is obtained from an even cycle
$\pm 3$
. Otherwise, there are only double edges and single edges. Since X is vertex-transitive, every vertex x has two neighbors, one is joined to x by a double edge, the other one by a single edge. It follows that X is obtained from an even cycle
![]() $C_{2n}$
by adding an edge in parallel to every second edge on the cycle. Let
$C_{2n}$
by adding an edge in parallel to every second edge on the cycle. Let
![]() $F_{2n}$
be the graph obtained from an even cycle
$F_{2n}$
be the graph obtained from an even cycle
![]() $C_{2n}$
by adding an edge in parallel to every second edge on the cycle. We will now determine the values of n for which
$C_{2n}$
by adding an edge in parallel to every second edge on the cycle. We will now determine the values of n for which
![]() $F_{2n}$
has
$F_{2n}$
has
![]() $1$
as a simple eigenvalue, in order to fully determine the class of cubic vertex-transitive graphs with 1 a simple eigenvalue, which contain at least one multiple edge.
$1$
as a simple eigenvalue, in order to fully determine the class of cubic vertex-transitive graphs with 1 a simple eigenvalue, which contain at least one multiple edge.
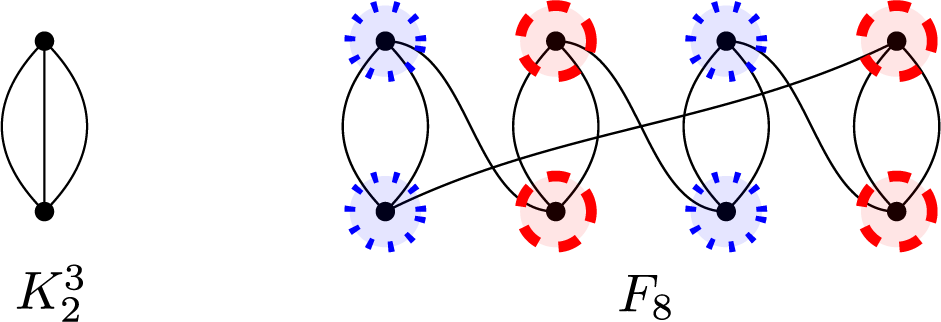
Figure 3:
![]() $F_{8}$
(left) is a regular cyclic cover of
$F_{8}$
(left) is a regular cyclic cover of
![]() $K_2^3$
(right); the top four vertices of
$K_2^3$
(right); the top four vertices of
![]() $F_8$
form the fiber corresponding to the top vertex of
$F_8$
form the fiber corresponding to the top vertex of
![]() $K_2^3$
and, likewise, the bottom vertices of
$K_2^3$
and, likewise, the bottom vertices of
![]() $F_8$
form the fiber corresponding to the bottom vertex of
$F_8$
form the fiber corresponding to the bottom vertex of
![]() $K_2^3$
. The partition given by the blue and red decorations on the vertices is the partition into
$K_2^3$
. The partition given by the blue and red decorations on the vertices is the partition into
![]() $V^+$
and
$V^+$
and
![]() $V^-$
.
$V^-$
.
We see that
![]() $F_{2n}$
has unique partition into sets
$F_{2n}$
has unique partition into sets
![]() $V^+$
and
$V^+$
and
![]() $V^-$
as in Lemma 4.1; the induced graphs on
$V^-$
as in Lemma 4.1; the induced graphs on
![]() $V^+$
and
$V^+$
and
![]() $V^-$
consist of m digons each, and thus n is even and
$V^-$
consist of m digons each, and thus n is even and
![]() $X = F_{4m}$
. Figure 3 shows this partition for
$X = F_{4m}$
. Figure 3 shows this partition for
![]() $F_8$
. Therefore, it has a unique
$F_8$
. Therefore, it has a unique
![]() $\pm 1$
eigenvector for eigenvalue
$\pm 1$
eigenvector for eigenvalue
![]() $\lambda =1$
. It is a simple exercise to exclude eigenvectors for
$\lambda =1$
. It is a simple exercise to exclude eigenvectors for
![]() $\lambda =1$
that are not multiples of this one. Instead of doing this, we note that
$\lambda =1$
that are not multiples of this one. Instead of doing this, we note that
![]() $F_{2n}$
is a regular cyclic cover over the two-vertex graph with triple edge,
$F_{2n}$
is a regular cyclic cover over the two-vertex graph with triple edge,
![]() $K_2^3$
(see Figure 3). Therefore, its eigenvalues are (see [Reference Kwak and Lee17] or [Reference Mohar and Tayfeh-Rezaie20] for details) the union of eigenvalues of n matrices of the form
$K_2^3$
(see Figure 3). Therefore, its eigenvalues are (see [Reference Kwak and Lee17] or [Reference Mohar and Tayfeh-Rezaie20] for details) the union of eigenvalues of n matrices of the form
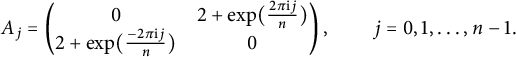 $$ \begin{align*}A_j = \begin{pmatrix} 0 & 2+\exp(\tfrac{2\pi \mathrm{i} j}{n}) \\ 2+\exp(\tfrac{-2\pi \mathrm{ i} j}{n}) & 0 \end{pmatrix}, \qquad j=0,1,\dots,n-1. \end{align*} $$
$$ \begin{align*}A_j = \begin{pmatrix} 0 & 2+\exp(\tfrac{2\pi \mathrm{i} j}{n}) \\ 2+\exp(\tfrac{-2\pi \mathrm{ i} j}{n}) & 0 \end{pmatrix}, \qquad j=0,1,\dots,n-1. \end{align*} $$
The matrix
![]() $A_j$
has eigenvalue 1 if and only if n is even and
$A_j$
has eigenvalue 1 if and only if n is even and
![]() $j=n/2$
. This gives the following result.
$j=n/2$
. This gives the following result.
Lemma 6.1 The eigenvalues of the graph
![]() $F_{2n}$
are
$F_{2n}$
are
Thus
![]() $\lambda =1$
is an eigenvalue if and only if n is even, in which case this is a simple eigenvalue.
$\lambda =1$
is an eigenvalue if and only if n is even, in which case this is a simple eigenvalue.
Proof A short computation shows that the eigenvalues of the matrix
![]() $A_j$
are
$A_j$
are
Such an eigenvalue is equal to 1 if and only if
![]() $\cos (2\pi j/n) = -1$
, i.e.,
$\cos (2\pi j/n) = -1$
, i.e.,
![]() $j=n/2$
.
$j=n/2$
.
6.2 Truncations of cubic arc-transitive graphs (type
 $C(m,3)$
)
$C(m,3)$
)
The truncation of a cubic multigraph G is a cubic graph
![]() $T(G)$
where every vertex v of G corresponds to a triangle in
$T(G)$
where every vertex v of G corresponds to a triangle in
![]() $T(G)$
and every edge
$T(G)$
and every edge
![]() $uv$
of G gives an edge of
$uv$
of G gives an edge of
![]() $T(G)$
between the triangles corresponding to u and v. Figure 4 shows two examples of truncations of cubic graphs. The truncation is isomorphic to the line graph of the subdivision of G. Thus, the eigenvalues of
$T(G)$
between the triangles corresponding to u and v. Figure 4 shows two examples of truncations of cubic graphs. The truncation is isomorphic to the line graph of the subdivision of G. Thus, the eigenvalues of
![]() $T(G)$
are easy to compute from the eigenvalues of G (see [Reference Cvetković, Doob and Sachs10] or [Reference Zhang, Chen and Chen30, Theorem 2.1]).
$T(G)$
are easy to compute from the eigenvalues of G (see [Reference Cvetković, Doob and Sachs10] or [Reference Zhang, Chen and Chen30, Theorem 2.1]).
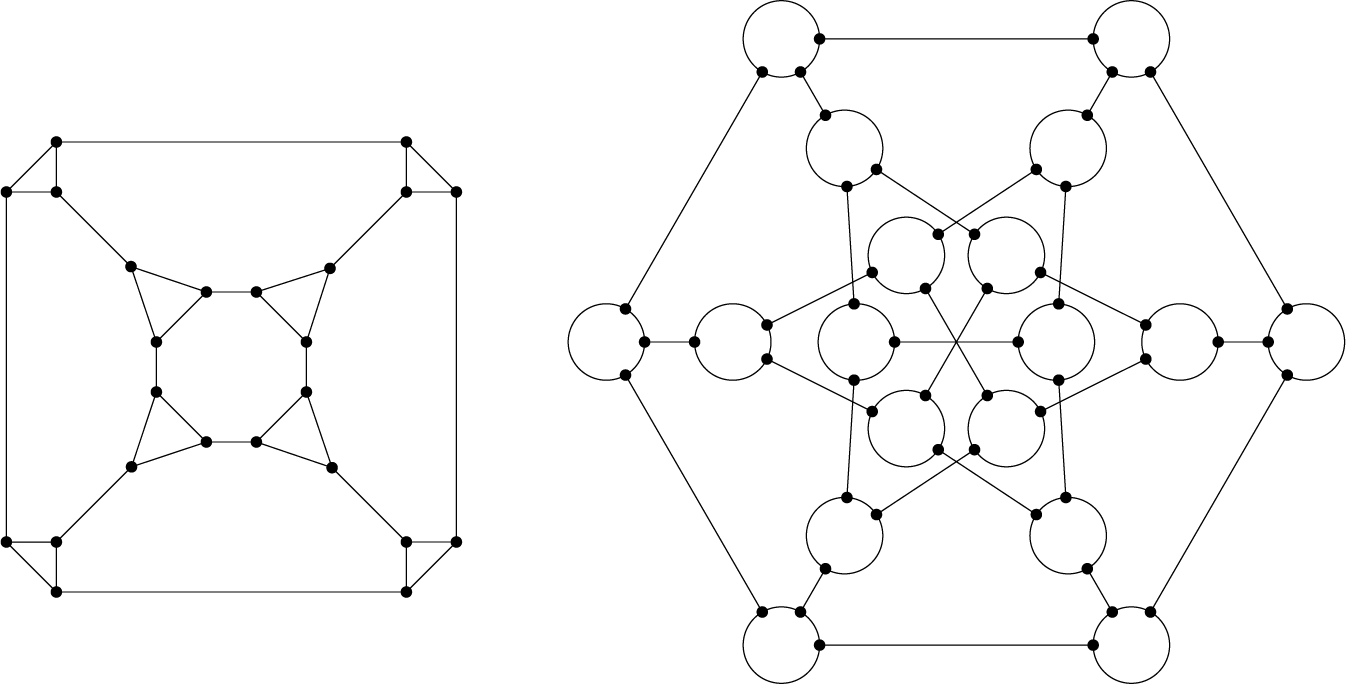
Figure 4: The truncation of the cube graph (left) and the truncation of the Pappus graph (right).
Theorem 6.2 If the eigenvalues of a cubic graph G are
![]() $\mu _1, \ldots , \mu _n$
, the eigenvalues of the truncation of G are
$\mu _1, \ldots , \mu _n$
, the eigenvalues of the truncation of G are
for
![]() $i = 1,\ldots , n$
and
$i = 1,\ldots , n$
and
![]() $-2$
and
$-2$
and
![]() $0$
, each with multiplicity
$0$
, each with multiplicity
![]() $\frac {n}{2}$
.
$\frac {n}{2}$
.
This implies the following result.
Corollary 6.3 For a connected cubic graph G, the following statements are equivalent:
-
(a) G is bipartite.
-
(b)
 $\lambda =1$
is an eigenvalue of the truncation
$\lambda =1$
is an eigenvalue of the truncation
 $T(G)$
of G.
$T(G)$
of G. -
(c)
 $\lambda =1$
is a simple eigenvalue of
$\lambda =1$
is a simple eigenvalue of
 $T(G)$
.
$T(G)$
.
Proof We see from Theorem 6.2 that
![]() $\lambda _i=1$
if and only if
$\lambda _i=1$
if and only if
![]() $\mu _i=-3$
. A connected cubic graph has
$\mu _i=-3$
. A connected cubic graph has
![]() $-3$
as an eigenvalue if and only if it is bipartite, in which case
$-3$
as an eigenvalue if and only if it is bipartite, in which case
![]() $-3$
is a simple eigenvalue (and hence
$-3$
is a simple eigenvalue (and hence
![]() $1$
is a simple eigenvalue of
$1$
is a simple eigenvalue of
![]() $T(G)$
).
$T(G)$
).
Corollary 6.4 If X is a connected vertex-transitive cubic graph containing a cycle of length 3, then X has 1 as a simple eigenvalue if and only if
![]() $X = T(G)$
, where G is a connected, bipartite, arc-transitive cubic multigraph.
$X = T(G)$
, where G is a connected, bipartite, arc-transitive cubic multigraph.
Proof First, we show that if X is vertex-transitive, contains a triangle, and has
![]() $1$
as a simple eigenvalue, then X must be the truncation of a graph G. Since X has
$1$
as a simple eigenvalue, then X must be the truncation of a graph G. Since X has
![]() $1$
as a simple eigenvalue, we may partition the vertices of X into cycles
$1$
as a simple eigenvalue, we may partition the vertices of X into cycles
![]() $V^+$
and
$V^+$
and
![]() $V^-$
, as in Lemma 4.1. Let v be vertex in
$V^-$
, as in Lemma 4.1. Let v be vertex in
![]() $V^+$
. We have that v is incident to a cycle of length
$V^+$
. We have that v is incident to a cycle of length
![]() $3$
, say T, in X. Since there is a matching between
$3$
, say T, in X. Since there is a matching between
![]() $V^+$
and
$V^+$
and
![]() $V^-$
, the triangle T does not use any edge of the matching. Thus, v must be incident to a cycle of length 3 in the subgraph of X induced by
$V^-$
, the triangle T does not use any edge of the matching. Thus, v must be incident to a cycle of length 3 in the subgraph of X induced by
![]() $V^+$
. Since
$V^+$
. Since
![]() $V^+$
induces a vertex-transitive
$V^+$
induces a vertex-transitive
![]() $2$
-regular subgraph of X by Lemma 4.1,
$2$
-regular subgraph of X by Lemma 4.1,
![]() $X[V^+]$
must be a disjoint union of cycles of length
$X[V^+]$
must be a disjoint union of cycles of length
![]() $3$
. The same holds for
$3$
. The same holds for
![]() $X[V^-]$
. Let G be obtained from X by contracting all the
$X[V^-]$
. Let G be obtained from X by contracting all the
![]() $3$
-cycles in
$3$
-cycles in
![]() $X[V^+]$
and
$X[V^+]$
and
![]() $X[V^-]$
. We see that G is cubic, since each vertex of X is incident to exactly
$X[V^-]$
. We see that G is cubic, since each vertex of X is incident to exactly
![]() $1$
edge which is not contracted to obtain G. By part (v) of Lemma 4.1, G is an arc-transitive bipartite graph, as claimed.
$1$
edge which is not contracted to obtain G. By part (v) of Lemma 4.1, G is an arc-transitive bipartite graph, as claimed.
The converse implication is clear by Corollary 6.3.
Since the cube graph and the Pappus graph are both cubic, arc-transitive, bipartite graphs, their truncations, as shown in Figure 4, are examples of cubic vertex-transitive graphs with
![]() $1$
as a simple eigenvalue.
$1$
as a simple eigenvalue.
6.3 Prisms and generalized Petersen graphs
In this section, we classify which prisms and which generalized Petersen graphs have
![]() $1$
as a simple eigenvalue.
$1$
as a simple eigenvalue.
The prism of order
![]() $2n$
is the Cartesian product of
$2n$
is the Cartesian product of
![]() $C_n$
with
$C_n$
with
![]() $K_2$
. The prism of order
$K_2$
. The prism of order
![]() $12$
appears in Figure 1. The eigenvalues of the prism graph of order
$12$
appears in Figure 1. The eigenvalues of the prism graph of order
![]() $2n$
are (see, e.g., [Reference Cvetković, Doob and Sachs10])
$2n$
are (see, e.g., [Reference Cvetković, Doob and Sachs10])
When
![]() $j=0$
, this gives the eigenvalue
$j=0$
, this gives the eigenvalue
![]() $1$
. Thus, a prism is a cubic vertex-transitive graph, which always has 1 as an eigenvalue. However, this eigenvalue is not always simple. This happens if and only if
$1$
. Thus, a prism is a cubic vertex-transitive graph, which always has 1 as an eigenvalue. However, this eigenvalue is not always simple. This happens if and only if
![]() $\cos \frac {2\pi j}{n} = 0$
for some j, which is the case if and only if
$\cos \frac {2\pi j}{n} = 0$
for some j, which is the case if and only if
![]() $j=n/4$
or
$j=n/4$
or
![]() $j=3n/4$
. This immediately gives the following characterization.
$j=3n/4$
. This immediately gives the following characterization.
Lemma 6.5 The prism of order
![]() $2n$
has
$2n$
has
![]() $\lambda = 1$
as simple eigenvalue if and only if
$\lambda = 1$
as simple eigenvalue if and only if
![]() $n \not \equiv 0\ (\bmod \ 4)$
.
$n \not \equiv 0\ (\bmod \ 4)$
.
Prisms are a special case of the generalized Petersen graphs, where the multiplicity of eigenvalue
![]() $1$
is relatively straightforward to understand. We now turn our attention to the more general case.
$1$
is relatively straightforward to understand. We now turn our attention to the more general case.
The generalized Petersen graph, denoted
![]() $P(n,k)$
, is the graph with vertex set
$P(n,k)$
, is the graph with vertex set
![]() $[n]\times [2]$
, where
$[n]\times [2]$
, where
![]() $[n] = \{1,\dots ,n\}$
, and each vertex
$[n] = \{1,\dots ,n\}$
, and each vertex
![]() $(j,1)$
is adjacent to
$(j,1)$
is adjacent to
![]() $(j,2)$
and to the vertices
$(j,2)$
and to the vertices
![]() $(j\pm 1,1)$
, while
$(j\pm 1,1)$
, while
![]() $(j,2)$
is adjacent to
$(j,2)$
is adjacent to
![]() $(j\pm k,2)$
, all operations taken modulo n. The well-known Petersen graph is isomorphic to
$(j\pm k,2)$
, all operations taken modulo n. The well-known Petersen graph is isomorphic to
![]() $P(5,2)$
, and the prism of order
$P(5,2)$
, and the prism of order
![]() $2n$
is isomorphic to
$2n$
is isomorphic to
![]() $P(n,1)$
. See Figure 5 for some other examples of generalized Petersen graphs.
$P(n,1)$
. See Figure 5 for some other examples of generalized Petersen graphs.
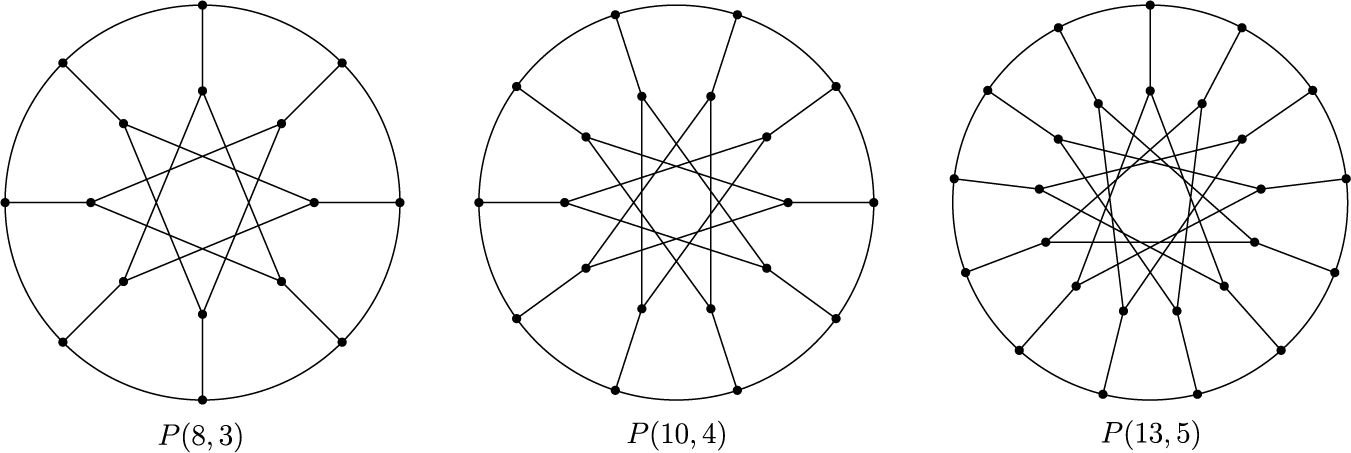
Figure 5: Examples of generalized Petersen graphs.
The vertex-transitivity of the generalized Petersen graphs is given in the following theorem.
Theorem 6.6 [Reference Frucht, Graver and Watkins11]
The generalized Petersen graph
![]() $P(n,k)$
is vertex-transitive if and only if
$P(n,k)$
is vertex-transitive if and only if
![]() $(n,k) = (10,2)$
or
$(n,k) = (10,2)$
or
![]() $k^2 \equiv \pm 1 \ (\bmod \ n)$
.
$k^2 \equiv \pm 1 \ (\bmod \ n)$
.
The following theorem gives the eigenvalues of
![]() $P(n,k)$
.
$P(n,k)$
.
Theorem 6.7 [Reference Gera and Stănică12]
The graph
![]() $P(n,k)$
has eigenvalues
$P(n,k)$
has eigenvalues
![]() $\delta $
for every root
$\delta $
for every root
![]() $\delta $
of
$\delta $
of
for
![]() $j = 0, \ldots , n-1$
, where
$j = 0, \ldots , n-1$
, where
The eigenvalues of
![]() $P(n,k)$
which are equal to 1 are solutions for equation (6.1) where
$P(n,k)$
which are equal to 1 are solutions for equation (6.1) where
![]() $x = 1$
, which we may simplify as
$x = 1$
, which we may simplify as
We may let
![]() $\theta = \frac {2\pi j}{n}$
and rewrite it as
$\theta = \frac {2\pi j}{n}$
and rewrite it as
Observe that
![]() $j=0$
gives a solution to this equation for any k. Hence, every generalized Petersen graph has eigenvalue
$j=0$
gives a solution to this equation for any k. Hence, every generalized Petersen graph has eigenvalue
![]() $1$
with multiplicity at least one.
$1$
with multiplicity at least one.
Theorem 6.8
![]() $P(n,k)$
has
$P(n,k)$
has
![]() $1$
as a simple eigenvalue if and only if one of the following holds:
$1$
as a simple eigenvalue if and only if one of the following holds:
-
(i)
 $4 \nmid n$
and
$4 \nmid n$
and
 $5 \nmid n$
.
$5 \nmid n$
. -
(ii)
 $4 \mid n$
and k is even.
$4 \mid n$
and k is even. -
(iii)
 $5 \mid n$
and
$5 \mid n$
and
 $k \notin \{ 2,3, n-3, n-2\}$
.
$k \notin \{ 2,3, n-3, n-2\}$
.
Proof As shown above, every
![]() $P(n,k)$
has eigenvalue 1 corresponding to the solution
$P(n,k)$
has eigenvalue 1 corresponding to the solution
![]() $j=0$
to (6.2). We note that solutions to (6.2) are equivalent to solution to (6.4) of the form
$j=0$
to (6.2). We note that solutions to (6.2) are equivalent to solution to (6.4) of the form
![]() $(j,jk)$
and thus we will make use of the solutions that we found in the proof of Lemma A.1. In light of this, Lemma A.2 shows that
$(j,jk)$
and thus we will make use of the solutions that we found in the proof of Lemma A.1. In light of this, Lemma A.2 shows that
![]() $1$
is a simple eigenvalue when
$1$
is a simple eigenvalue when
![]() $4 \nmid n$
and
$4 \nmid n$
and
![]() $5 \nmid n$
.
$5 \nmid n$
.
Suppose now that
![]() $n = 4a$
, where a is an integer. If
$n = 4a$
, where a is an integer. If
![]() $k \equiv 1 \pmod 4$
(resp.
$k \equiv 1 \pmod 4$
(resp.
![]() $k \equiv 3 \pmod 4$
), we see that
$k \equiv 3 \pmod 4$
), we see that
![]() $j=a$
(resp.
$j=a$
(resp.
![]() $j=3a$
) is a nontrivial solution to (6.2). Suppose now that k is even. By Lemma A.2, if
$j=3a$
) is a nontrivial solution to (6.2). Suppose now that k is even. By Lemma A.2, if
![]() $4 | n$
, the only nontrivial solution to (6.4) are when
$4 | n$
, the only nontrivial solution to (6.4) are when
![]() $\left \{ \frac {j}{n},\frac {\ell }{n} \right \} \subseteq \left \{ \frac {1}{4},\frac {3}{4} \right \}$
. In the case for the generalized Petersen graphs, solutions to (6.4) where
$\left \{ \frac {j}{n},\frac {\ell }{n} \right \} \subseteq \left \{ \frac {1}{4},\frac {3}{4} \right \}$
. In the case for the generalized Petersen graphs, solutions to (6.4) where
![]() $\ell = kj$
are exactly the solution to (6.2). We see that if k is even, then
$\ell = kj$
are exactly the solution to (6.2). We see that if k is even, then
![]() $\left \{ \frac {j}{n},\frac {jk}{n} \right \}$
is either
$\left \{ \frac {j}{n},\frac {jk}{n} \right \}$
is either
![]() $\left \{ \frac {1}{4},\frac {k}{4} \right \}$
or
$\left \{ \frac {1}{4},\frac {k}{4} \right \}$
or
![]() $\left \{ \frac {3}{4},\frac {3k}{4} \right \}$
, neither of which can be a subset of
$\left \{ \frac {3}{4},\frac {3k}{4} \right \}$
, neither of which can be a subset of
![]() $\left \{ \frac {1}{4},\frac {3}{4} \right \}$
since k is even. Thus, in this case,
$\left \{ \frac {1}{4},\frac {3}{4} \right \}$
since k is even. Thus, in this case,
![]() $1$
is a simple eigenvalue.
$1$
is a simple eigenvalue.
Suppose now that
![]() $5 \mid n$
. By Lemma A.2, if
$5 \mid n$
. By Lemma A.2, if
![]() $n = 5a$
, the only nontrivial solutions to (6.4) are
$n = 5a$
, the only nontrivial solutions to (6.4) are
![]() $(j,\ell ) \in \{a, 4a\}\times \{2a, 3a\} \cup \{2a, 3a\} \times \{a, 4a\}$
. Again, we need solutions to (6.4) where
$(j,\ell ) \in \{a, 4a\}\times \{2a, 3a\} \cup \{2a, 3a\} \times \{a, 4a\}$
. Again, we need solutions to (6.4) where
![]() $\ell = kj \mod 5a$
. We summarize the values of
$\ell = kj \mod 5a$
. We summarize the values of
![]() $j, \ell $
, and k that we obtain in Table 1.
$j, \ell $
, and k that we obtain in Table 1.
Thus, we get additional solution if and only if
![]() $k \in \{ 2,3, n-3, n-2\} \mod n$
.
$k \in \{ 2,3, n-3, n-2\} \mod n$
.
For the examples in Figure 5, we see by Theorem 6.8 that
![]() $P(10,4)$
and
$P(10,4)$
and
![]() $P(13,5)$
have
$P(13,5)$
have
![]() $1$
as a simple eigenvalue, while
$1$
as a simple eigenvalue, while
![]() $P(8,3)$
does not. In fact,
$P(8,3)$
does not. In fact,
![]() $P(13,5)$
is the smallest generalized Petersen graph with
$P(13,5)$
is the smallest generalized Petersen graph with
![]() $1$
as a simple eigenvalues, which is not isomorphic to a prism.
$1$
as a simple eigenvalues, which is not isomorphic to a prism.
6.4 Regular embeddings of
 $K_{m,m}$
$K_{m,m}$
In this section, we consider the truncation,
![]() $T_m$
, of regular embeddings of the complete bipartite graph
$T_m$
, of regular embeddings of the complete bipartite graph
![]() $K_{m,m}$
. This is an application of the ideas from Section 5. Here, we characterize which orders of m give graphs where
$K_{m,m}$
. This is an application of the ideas from Section 5. Here, we characterize which orders of m give graphs where
![]() $1$
is a simple eigenvalue, using results on vanishing sums of roots of unity and sums of cosines, which are included in Appendix A.
$1$
is a simple eigenvalue, using results on vanishing sums of roots of unity and sums of cosines, which are included in Appendix A.
For
![]() $m\ge 3$
, let
$m\ge 3$
, let
![]() $T_m$
be the cubic graph of order
$T_m$
be the cubic graph of order
![]() $2m^2$
defined in the following way. The vertices of
$2m^2$
defined in the following way. The vertices of
![]() $T_m$
are
$T_m$
are
![]() $\{v_{i, j}, w_{i, j} \mid i, j \in {\mathbb Z}_m\}$
. The edges are
$\{v_{i, j}, w_{i, j} \mid i, j \in {\mathbb Z}_m\}$
. The edges are
for all
![]() $i, j \in {\mathbb Z}_m$
. It is easy to see that
$i, j \in {\mathbb Z}_m$
. It is easy to see that
![]() $T_m$
is a cubic, vertex-transitive graph with 1 as an eigenvalue, not necessarily simple, by considering the eigenvector that is
$T_m$
is a cubic, vertex-transitive graph with 1 as an eigenvalue, not necessarily simple, by considering the eigenvector that is
![]() $+1$
on every vertex
$+1$
on every vertex
![]() $v_{i, j}$
and
$v_{i, j}$
and
![]() $-1$
on every vertex
$-1$
on every vertex
![]() $w_{i, j}$
. Figure 6 shows
$w_{i, j}$
. Figure 6 shows
![]() $T_3$
and
$T_3$
and
![]() $T_4$
.
$T_4$
.
Figure 6: The graphs
![]() $T_3$
(left) and
$T_3$
(left) and
![]() $T_4$
(right). The vertex labels have been repressed for
$T_4$
(right). The vertex labels have been repressed for
![]() $T_4$
, for readability, but can be easily inferred from those for
$T_4$
, for readability, but can be easily inferred from those for
![]() $T_3$
.
$T_3$
.
Alternatively, we can construct
![]() $T_m$
from the regular embedding of
$T_m$
from the regular embedding of
![]() $K_{m,m}$
, given by Nedela and Škoviera in [Reference Nedela and Škoviera22]. We consider
$K_{m,m}$
, given by Nedela and Škoviera in [Reference Nedela and Škoviera22]. We consider
![]() $K_{m,m}$
as a Cayley graph on
$K_{m,m}$
as a Cayley graph on
![]() ${\mathbb Z}_{2m}$
with the connection set
${\mathbb Z}_{2m}$
with the connection set
![]() $\{1, 3, 5, \ldots , 2m-1\}$
as the generating set. The rotation system
$\{1, 3, 5, \ldots , 2m-1\}$
as the generating set. The rotation system
![]() $\Pi $
has vertex rotations at each vertex given by the cyclic permutation
$\Pi $
has vertex rotations at each vertex given by the cyclic permutation
![]() $(1, 3, 5, \ldots , 2m-1)$
of the generators. The graph
$(1, 3, 5, \ldots , 2m-1)$
of the generators. The graph
![]() $T_m$
is isomorphic to the vertex truncation
$T_m$
is isomorphic to the vertex truncation
![]() $T(K_{m,m}, \Pi )$
.
$T(K_{m,m}, \Pi )$
.
Let B be the
![]() $m^2 \times m^2$
matrix such that
$m^2 \times m^2$
matrix such that
![]() $B = I_m \otimes C_m$
, where
$B = I_m \otimes C_m$
, where
![]() $C_m$
is the adjacency matrix of the cycle of order m and
$C_m$
is the adjacency matrix of the cycle of order m and
![]() $I_m$
is the
$I_m$
is the
![]() $m\times m$
identity matrix. Let P be the permutation matrix indexed by
$m\times m$
identity matrix. Let P be the permutation matrix indexed by
![]() ${\mathbb Z}_m \times {\mathbb Z}_m$
such that P takes
${\mathbb Z}_m \times {\mathbb Z}_m$
such that P takes
![]() $(i,j)$
to
$(i,j)$
to
![]() $(j,i)$
. The adjacency matrix of
$(j,i)$
. The adjacency matrix of
![]() $T_m$
can be written as
$T_m$
can be written as
 $$\begin{align*}A := A(T_m) = \begin{pmatrix} B & I \\ I & P^TBP \end{pmatrix}. \end{align*}$$
$$\begin{align*}A := A(T_m) = \begin{pmatrix} B & I \\ I & P^TBP \end{pmatrix}. \end{align*}$$
Observe that
![]() $P^2 = I$
and
$P^2 = I$
and
![]() $P = P^T$
. By definition, we see that
$P = P^T$
. By definition, we see that
where
![]() $e_k$
denotes the kth elementary basis vector. Then, for any
$e_k$
denotes the kth elementary basis vector. Then, for any
![]() $m\times 1$
vectors
$m\times 1$
vectors
![]() ${\mathbf v}$
and
${\mathbf v}$
and
![]() ${\mathbf w}$
, we see that
${\mathbf w}$
, we see that
Theorem 6.9 The eigenvalues of
![]() $T_m$
are
$T_m$
are
for all
![]() $(j, \ell ) \in {\mathbb Z}_m \times {\mathbb Z}_m$
.
$(j, \ell ) \in {\mathbb Z}_m \times {\mathbb Z}_m$
.
Proof To find these eigenvalues, we use the proof method developed in [Reference Gera and Stănică12] in order to find the eigenvalues of generalized Petersen graphs. Let
![]() ${\mathbf v}, {\mathbf w}$
be eigenvectors of
${\mathbf v}, {\mathbf w}$
be eigenvectors of
![]() $C_m$
with eigenvalues
$C_m$
with eigenvalues
![]() $\lambda $
and
$\lambda $
and
![]() $\theta $
, respectively. Then
$\theta $
, respectively. Then
and
Let V be an eigenbasis for
![]() $C_m$
in
$C_m$
in
![]() ${\mathbb R}^m$
. Then the basis
${\mathbb R}^m$
. Then the basis
of
![]() ${\mathbb R}^{m^2}$
simultaneously diagonalizes B and
${\mathbb R}^{m^2}$
simultaneously diagonalizes B and
![]() $P^T BP$
. We construct an eigenbasis U of A over
$P^T BP$
. We construct an eigenbasis U of A over
![]() ${\mathbb R}^{2m^2}$
such that the elements of U are
${\mathbb R}^{2m^2}$
such that the elements of U are
 $$\begin{align*}\begin{pmatrix} \alpha {\mathbf v} \otimes {\mathbf w} \\ {\mathbf v} \otimes {\mathbf w} \end{pmatrix}, \end{align*}$$
$$\begin{align*}\begin{pmatrix} \alpha {\mathbf v} \otimes {\mathbf w} \\ {\mathbf v} \otimes {\mathbf w} \end{pmatrix}, \end{align*}$$
where
![]() ${\mathbf v},{\mathbf w} \in V$
with eigenvalues
${\mathbf v},{\mathbf w} \in V$
with eigenvalues
![]() $\lambda $
and
$\lambda $
and
![]() $\theta $
, respectively, and
$\theta $
, respectively, and
![]() $\alpha = \delta -\lambda $
for each
$\alpha = \delta -\lambda $
for each
![]() $\delta $
a solution to
$\delta $
a solution to
Observe that since
 $$\begin{align*}2\left(\frac{\theta + \lambda}{2} \right)^2 = \frac{\theta^2 + \lambda^2}{2} + \theta\lambda> \theta \lambda -1 \end{align*}$$
$$\begin{align*}2\left(\frac{\theta + \lambda}{2} \right)^2 = \frac{\theta^2 + \lambda^2}{2} + \theta\lambda> \theta \lambda -1 \end{align*}$$
for any
![]() $\lambda , \theta \in {\mathbb R}$
, equation (6.3) always has two distinct solutions for
$\lambda , \theta \in {\mathbb R}$
, equation (6.3) always has two distinct solutions for
![]() $\delta $
. The set U consists of
$\delta $
. The set U consists of
![]() $2m^2$
linearly independent vectors in
$2m^2$
linearly independent vectors in
![]() ${\mathbb R}^{2m^2}$
. We now verify that each element of U is an eigenvector of A by observing
${\mathbb R}^{2m^2}$
. We now verify that each element of U is an eigenvector of A by observing
 $$\begin{align*}\begin{aligned} A \begin{pmatrix} \alpha {\mathbf v} \otimes {\mathbf w} \\ {\mathbf v} \otimes {\mathbf w} \end{pmatrix} &= \begin{pmatrix} B & I \\ I & P^TBP \end{pmatrix} \begin{pmatrix} \alpha {\mathbf v} \otimes {\mathbf w} \\ {\mathbf v} \otimes {\mathbf w} \end{pmatrix} \\ &= \begin{pmatrix} \alpha \theta {\mathbf v} \otimes {\mathbf w} + {\mathbf v} \otimes {\mathbf w} \\ \alpha {\mathbf v} \otimes {\mathbf w} + \lambda {\mathbf v} \otimes {\mathbf w} \end{pmatrix} \\ &= \begin{pmatrix} (\alpha \theta + 1) {\mathbf v} \otimes {\mathbf w} \\ (\alpha + \lambda){\mathbf v} \otimes {\mathbf w} \end{pmatrix}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} A \begin{pmatrix} \alpha {\mathbf v} \otimes {\mathbf w} \\ {\mathbf v} \otimes {\mathbf w} \end{pmatrix} &= \begin{pmatrix} B & I \\ I & P^TBP \end{pmatrix} \begin{pmatrix} \alpha {\mathbf v} \otimes {\mathbf w} \\ {\mathbf v} \otimes {\mathbf w} \end{pmatrix} \\ &= \begin{pmatrix} \alpha \theta {\mathbf v} \otimes {\mathbf w} + {\mathbf v} \otimes {\mathbf w} \\ \alpha {\mathbf v} \otimes {\mathbf w} + \lambda {\mathbf v} \otimes {\mathbf w} \end{pmatrix} \\ &= \begin{pmatrix} (\alpha \theta + 1) {\mathbf v} \otimes {\mathbf w} \\ (\alpha + \lambda){\mathbf v} \otimes {\mathbf w} \end{pmatrix}. \end{aligned} \end{align*}$$
But
![]() $\alpha $
has been carefully chosen such that
$\alpha $
has been carefully chosen such that
![]() $\alpha + \lambda = \delta $
and
$\alpha + \lambda = \delta $
and
![]() $\alpha \lambda + 1 = \delta \alpha $
, so
$\alpha \lambda + 1 = \delta \alpha $
, so
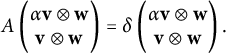 $$\begin{align*}A \begin{pmatrix} \alpha {\mathbf v} \otimes {\mathbf w} \\ {\mathbf v} \otimes {\mathbf w} \end{pmatrix} = \delta \begin{pmatrix} \alpha {\mathbf v} \otimes {\mathbf w} \\ {\mathbf v} \otimes {\mathbf w} \end{pmatrix}. \end{align*}$$
$$\begin{align*}A \begin{pmatrix} \alpha {\mathbf v} \otimes {\mathbf w} \\ {\mathbf v} \otimes {\mathbf w} \end{pmatrix} = \delta \begin{pmatrix} \alpha {\mathbf v} \otimes {\mathbf w} \\ {\mathbf v} \otimes {\mathbf w} \end{pmatrix}. \end{align*}$$
Then U is an eigenbasis for A, as claimed, and the eigenvalues of A are the solution for
![]() $\delta $
in equation (6.3) where
$\delta $
in equation (6.3) where
![]() $\theta $
and
$\theta $
and
![]() $\lambda $
range over the eigenvalues of
$\lambda $
range over the eigenvalues of
![]() $C_k$
. We use the quadratic formula to see that
$C_k$
. We use the quadratic formula to see that
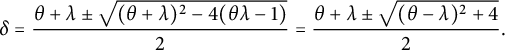 $$\begin{align*}\delta = \frac{\theta + \lambda \pm \sqrt{(\theta + \lambda)^2 - 4(\theta \lambda - 1) }}{2} = \frac{\theta + \lambda \pm \sqrt{(\theta - \lambda)^2 + 4 }}{2}. \end{align*}$$
$$\begin{align*}\delta = \frac{\theta + \lambda \pm \sqrt{(\theta + \lambda)^2 - 4(\theta \lambda - 1) }}{2} = \frac{\theta + \lambda \pm \sqrt{(\theta - \lambda)^2 + 4 }}{2}. \end{align*}$$
The eigenvalues of
![]() $C_m$
are
$C_m$
are
![]() $2\cos \tfrac {2\pi j}{m}$
for
$2\cos \tfrac {2\pi j}{m}$
for
![]() $j \in {\mathbb Z}_m$
(see [Reference Brouwer and Haemers3] or [Reference Cvetković, Doob and Sachs10]). Putting these values in place of
$j \in {\mathbb Z}_m$
(see [Reference Brouwer and Haemers3] or [Reference Cvetković, Doob and Sachs10]). Putting these values in place of
![]() $\theta $
and
$\theta $
and
![]() $\lambda $
, we obtain the expressions given by the theorem.
$\lambda $
, we obtain the expressions given by the theorem.
By restricting our attention to the eigenvalue 1, we have the following consequence of Theorem 6.9.
Corollary 6.10 The multiplicity of
![]() $1$
as an eigenvalue of the graph
$1$
as an eigenvalue of the graph
![]() $T_{m}$
is equal to the number of solutions
$T_{m}$
is equal to the number of solutions
![]() $(j, \ell )$
to the equation:
$(j, \ell )$
to the equation:
where
![]() $j, \ell \in \{0, \ldots , m -1\}$
.
$j, \ell \in \{0, \ldots , m -1\}$
.
Proof Let
![]() $a = \cos \tfrac {2\pi j}{m}$
and
$a = \cos \tfrac {2\pi j}{m}$
and
![]() $b = \cos \tfrac {2\pi \ell }{m}$
. By Theorem 6.9, we are looking for the number of pairs
$b = \cos \tfrac {2\pi \ell }{m}$
. By Theorem 6.9, we are looking for the number of pairs
![]() $(j,\ell )$
for which
$(j,\ell )$
for which
![]() $a+b-1=\pm \sqrt {(a-b)^2+1}$
. For
$a+b-1=\pm \sqrt {(a-b)^2+1}$
. For
![]() $a=b$
, this is satisfied precisely when
$a=b$
, this is satisfied precisely when
![]() $a=b=1$
and when
$a=b=1$
and when
![]() $a=b=0$
, both of which provide solutions for (6.4). On the other hand, if
$a=b=0$
, both of which provide solutions for (6.4). On the other hand, if
![]() $a\ne b$
, then the value under the square root is bigger than 1, which implies that the solutions must satisfy the equation
$a\ne b$
, then the value under the square root is bigger than 1, which implies that the solutions must satisfy the equation
![]() $a+b-1 = -\sqrt {(a-b)^2+1}$
. For values
$a+b-1 = -\sqrt {(a-b)^2+1}$
. For values
![]() $a,b$
that are smaller or equal to 1, this is equivalent to
$a,b$
that are smaller or equal to 1, this is equivalent to
![]() $(a+b-1)^2 = (a-b)^2 +1$
, which holds if and only (6.4) holds.
$(a+b-1)^2 = (a-b)^2 +1$
, which holds if and only (6.4) holds.
Theorem 6.11
![]() $T_m$
has
$T_m$
has
![]() $1$
as a simple eigenvalue if and only if
$1$
as a simple eigenvalue if and only if
![]() $4 \nmid m$
and
$4 \nmid m$
and
![]() $5 \nmid m$
.
$5 \nmid m$
.
The theorem follows from Corollary 6.10 by Lemmas A.1 and A.2 that are proved in Appendix A.
A Sums of cosines
The multiplicity of
![]() $1$
as an eigenvalue of the graph
$1$
as an eigenvalue of the graph
![]() $T_{m}$
is equal to the number of solutions
$T_{m}$
is equal to the number of solutions
![]() $(j, \ell )$
to equation (6.4). We observe that, if we set
$(j, \ell )$
to equation (6.4). We observe that, if we set
![]() $\ell =kj$
, we obtain exactly (6.2) in Section 6.3. Note that this equation is always satisfied for
$\ell =kj$
, we obtain exactly (6.2) in Section 6.3. Note that this equation is always satisfied for
![]() $j = \ell = 0$
, which we will refer to as the trivial solution.
$j = \ell = 0$
, which we will refer to as the trivial solution.
We will first determine that when
![]() $4 |m$
or
$4 |m$
or
![]() $5|m$
, equation (6.4) has nontrivial solutions. Then we will show that there are no nontrivial solutions in the other cases.
$5|m$
, equation (6.4) has nontrivial solutions. Then we will show that there are no nontrivial solutions in the other cases.
Lemma A.1 If
![]() $4$
divides m, then (6.4) has at least four nontrivial solutions. If
$4$
divides m, then (6.4) has at least four nontrivial solutions. If
![]() $5$
divides m, then (6.4) has at least eight nontrivial solutions.
$5$
divides m, then (6.4) has at least eight nontrivial solutions.
Proof We will describe additional solutions to (6.4) when m is divisible by
![]() $4$
and when m is divisible by
$4$
and when m is divisible by
![]() $5$
. Note that
$5$
. Note that
Then, if
![]() $m = 4a$
for some a, then for each
$m = 4a$
for some a, then for each
we obtain a solution to (6.4).
Similarly, suppose now that
![]() $m = 5a$
for some a. We note that
$m = 5a$
for some a. We note that
and we see that
and
 $$\begin{align*}2\,\cos\tfrac{2\pi}{5} \cos\tfrac{4\pi}{5} = \frac{\left(-1 + \sqrt{5}\,\right)\left(-1 - \sqrt{5}\,\right)}{8} = -\frac{1}{2}. \end{align*}$$
$$\begin{align*}2\,\cos\tfrac{2\pi}{5} \cos\tfrac{4\pi}{5} = \frac{\left(-1 + \sqrt{5}\,\right)\left(-1 - \sqrt{5}\,\right)}{8} = -\frac{1}{2}. \end{align*}$$
Then let
![]() $A = \{a, 4a\}$
and
$A = \{a, 4a\}$
and
![]() $B = \{2a, 3a\}$
. For every choice of
$B = \{2a, 3a\}$
. For every choice of
![]() $j\in A$
and
$j\in A$
and
![]() $\ell \in B$
(or vice versa), we obtain distinct solution
$\ell \in B$
(or vice versa), we obtain distinct solution
![]() $(j,\ell )$
to equation (6.4).
$(j,\ell )$
to equation (6.4).
Solutions of equation (6.4) can be limited further by using an old result of Conway and Jones [Reference Conway and Jones8].
Lemma A.2 If
![]() $4 \nmid m$
and
$4 \nmid m$
and
![]() $5 \nmid m$
, then (6.4) has only the trivial solution. Further, if
$5 \nmid m$
, then (6.4) has only the trivial solution. Further, if
![]() $4 | m$
, the only nontrivial solution is
$4 | m$
, the only nontrivial solution is
![]() $\left \{ \frac {j}{m},\frac {\ell }{m} \right \} \subseteq \left \{ \frac {1}{4},\frac {3}{4} \right \}$
. If
$\left \{ \frac {j}{m},\frac {\ell }{m} \right \} \subseteq \left \{ \frac {1}{4},\frac {3}{4} \right \}$
. If
![]() $ m = 5a$
, the only nontrivial solution is
$ m = 5a$
, the only nontrivial solution is
![]() $(j,\ell ) \in \{a, 4a\}\times \{2a, 3a\}\cup \{2a, 3a\} \times \{a, 4a\}$
.
$(j,\ell ) \in \{a, 4a\}\times \{2a, 3a\}\cup \{2a, 3a\} \times \{a, 4a\}$
.
Proof We will make extensive use of [Reference Conway and Jones8, Theorem 7], which gives the complete description of solutions to the equation
where all variables
![]() $A,\dots ,E$
and
$A,\dots ,E$
and
![]() $a,b,c,d$
are rational numbers. We may use an elementary trigonometric identity for cosine of angle sums to rewrite (6.4) as follows:
$a,b,c,d$
are rational numbers. We may use an elementary trigonometric identity for cosine of angle sums to rewrite (6.4) as follows:
where
![]() $x = 2\pi \frac {j}{m}$
and
$x = 2\pi \frac {j}{m}$
and
![]() $y = 2 \pi \frac {\ell }{m}$
. This is a special case of (A.1) with
$y = 2 \pi \frac {\ell }{m}$
. This is a special case of (A.1) with
![]() $A=B=1$
,
$A=B=1$
,
![]() $C=D=-1$
, and
$C=D=-1$
, and
![]() $E=0$
. Observe that if
$E=0$
. Observe that if
![]() $y' = 2\pi - y$
, then
$y' = 2\pi - y$
, then
Without loss of generality, we may therefore assume that
![]() $0 \leq x \leq y \leq \pi $
. Let
$0 \leq x \leq y \leq \pi $
. Let
We will consider the following cases:
-
(i) There exists
 $c \in {\mathcal C}$
such that c is rational.
$c \in {\mathcal C}$
such that c is rational. -
(ii)
 ${\mathcal C} \cap {\mathbb Q} = \emptyset $
and some two elements of
${\mathcal C} \cap {\mathbb Q} = \emptyset $
and some two elements of
 ${\mathcal C}$
have rational sum.
${\mathcal C}$
have rational sum. -
(iii) No proper subset of
 ${\mathcal C}$
has rational sum.
${\mathcal C}$
has rational sum.
Case (i). It is known that if
![]() $\cos \theta \in {\mathbb Q}$
and
$\cos \theta \in {\mathbb Q}$
and
![]() $\theta $
is a rational multiple of
$\theta $
is a rational multiple of
![]() $\pi $
, then
$\pi $
, then
![]() $\cos \theta \in \{\pm 1, \pm \frac {1}{2},0\}$
.
$\cos \theta \in \{\pm 1, \pm \frac {1}{2},0\}$
.
We first suppose
![]() $\cos x \in {\mathbb Q}$
. If
$\cos x \in {\mathbb Q}$
. If
![]() $\cos x = 1$
, then (A.2) implies that
$\cos x = 1$
, then (A.2) implies that
![]() $1 + \cos y = 2 \cos y$
. Then
$1 + \cos y = 2 \cos y$
. Then
![]() $x = y = 0$
, giving the trivial solution. If
$x = y = 0$
, giving the trivial solution. If
![]() $\cos x = \frac {1}{2}$
, then (A.2) implies that
$\cos x = \frac {1}{2}$
, then (A.2) implies that
![]() $\frac {1}{2} + \cos y = \cos y$
, which is impossible. Similarly, if
$\frac {1}{2} + \cos y = \cos y$
, which is impossible. Similarly, if
![]() $\cos x = -\frac {1}{2}$
, then (A.2) implies that
$\cos x = -\frac {1}{2}$
, then (A.2) implies that
![]() $-\frac {1}{2} + \cos y = - \cos y$
and
$-\frac {1}{2} + \cos y = - \cos y$
and
![]() $\cos y = \frac {1}{4} \in {\mathbb Q}$
, which is not possible since y is a rational multiple of
$\cos y = \frac {1}{4} \in {\mathbb Q}$
, which is not possible since y is a rational multiple of
![]() $\pi $
.
$\pi $
.
If
![]() $\cos x = -1$
, then (A.2) implies that
$\cos x = -1$
, then (A.2) implies that
![]() $-1 + \cos y = -2 \cos y$
, which gives that
$-1 + \cos y = -2 \cos y$
, which gives that
![]() $\cos y = \frac {1}{3}$
. Since y is a rational multiple of
$\cos y = \frac {1}{3}$
. Since y is a rational multiple of
![]() $\pi $
, this is impossible. If
$\pi $
, this is impossible. If
![]() $\cos x = 0$
, then (A.2) implies that
$\cos x = 0$
, then (A.2) implies that
![]() $\cos y = 0$
. In this case,
$\cos y = 0$
. In this case,
![]() $x,y \in \left \{\frac {\pi }{2}, \frac {3\pi }{2}\right \}$
and
$x,y \in \left \{\frac {\pi }{2}, \frac {3\pi }{2}\right \}$
and
![]() $\frac {j}{m}, \frac {\ell }{m} \in \left \{\frac {1}{4},\frac {3}{4}\right \}$
. Then
$\frac {j}{m}, \frac {\ell }{m} \in \left \{\frac {1}{4},\frac {3}{4}\right \}$
. Then
![]() $4 | m$
and
$4 | m$
and
![]() $\frac {j}{m}, \frac {\ell }{m} \in \left \{\frac {1}{4},\frac {3}{4}\right \}$
give all nontrivial solutions when some
$\frac {j}{m}, \frac {\ell }{m} \in \left \{\frac {1}{4},\frac {3}{4}\right \}$
give all nontrivial solutions when some
![]() $c \in C$
is rational.
$c \in C$
is rational.
Since (A.2) is symmetric in x and y, we may now assume that both
![]() $\cos x$
and
$\cos x$
and
![]() $\cos y$
are irrational.
$\cos y$
are irrational.
If both
![]() $\cos (x +y)$
and
$\cos (x +y)$
and
![]() $\cos (x-y)$
are rational, then
$\cos (x-y)$
are rational, then
![]() $\cos x + \cos y \in {\mathbb Q}$
and
$\cos x + \cos y \in {\mathbb Q}$
and
![]() $\cos x, \cos y \notin {\mathbb Q}$
. Note that
$\cos x, \cos y \notin {\mathbb Q}$
. Note that
![]() $x, y \notin \{ 0, \pi , \frac {\pi }{2}\}$
. Let
$x, y \notin \{ 0, \pi , \frac {\pi }{2}\}$
. Let
![]() $\phi (\theta )$
be the following:
$\phi (\theta )$
be the following:
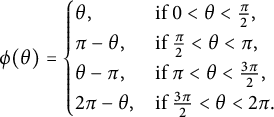 $$\begin{align*}\phi(\theta) = \begin{cases} \theta, & \text{if } 0 < \theta < \frac{\pi}{2}, \\ \pi - \theta, & \text{if } \frac{\pi}{2}< \theta < \pi, \\ \theta - \pi, & \text{if } \pi < \theta < \frac{3\pi}{2}, \\ 2\pi - \theta, & \text{if } \frac{3\pi}{2}< \theta < 2\pi. \end{cases} \end{align*}$$
$$\begin{align*}\phi(\theta) = \begin{cases} \theta, & \text{if } 0 < \theta < \frac{\pi}{2}, \\ \pi - \theta, & \text{if } \frac{\pi}{2}< \theta < \pi, \\ \theta - \pi, & \text{if } \pi < \theta < \frac{3\pi}{2}, \\ 2\pi - \theta, & \text{if } \frac{3\pi}{2}< \theta < 2\pi. \end{cases} \end{align*}$$
Then we note that
![]() $\cos (\phi (x)) \pm \cos (\phi (y)) \in {\mathbb Q}$
and
$\cos (\phi (x)) \pm \cos (\phi (y)) \in {\mathbb Q}$
and
![]() $\cos (\phi (x)), \cos (\phi (y)) \notin {\mathbb Q}$
. We can apply Theorem 7 of [Reference Conway and Jones8] to obtain that
$\cos (\phi (x)), \cos (\phi (y)) \notin {\mathbb Q}$
. We can apply Theorem 7 of [Reference Conway and Jones8] to obtain that
![]() $ a\cos (\phi (x)) + b\cos (\phi (y)) = q$
for some
$ a\cos (\phi (x)) + b\cos (\phi (y)) = q$
for some
![]() $q \in {\mathbb Q}$
is proportional to
$q \in {\mathbb Q}$
is proportional to
![]() $\cos \frac {\pi }{5} - \cos \frac {2\pi }{5} = \frac {1}{2}$
. This implies that
$\cos \frac {\pi }{5} - \cos \frac {2\pi }{5} = \frac {1}{2}$
. This implies that
![]() $5$
divides m and we can see that the only additional solutions are the ones found in Lemma A.1.
$5$
divides m and we can see that the only additional solutions are the ones found in Lemma A.1.
In the remainder of Case (i), we may assume that exactly one of
![]() $\cos (x +y)$
and
$\cos (x +y)$
and
![]() $\cos (x-y)$
is rational. Let
$\cos (x-y)$
is rational. Let
![]() $\theta $
be the corresponding argument. We may also assume that no rational linear combination of a proper subset of
$\theta $
be the corresponding argument. We may also assume that no rational linear combination of a proper subset of
![]() ${\mathcal C} \setminus \{\cos \theta \}$
has a rational sum. Let
${\mathcal C} \setminus \{\cos \theta \}$
has a rational sum. Let
![]() $\tau $
be the argument of the irrational element of
$\tau $
be the argument of the irrational element of
![]() $\{ \cos (x +y), \cos (x-y)\}$
. Since cosine is an even function, we may take
$\{ \cos (x +y), \cos (x-y)\}$
. Since cosine is an even function, we may take
![]() $y-x$
instead of
$y-x$
instead of
![]() $x-y$
and assume that
$x-y$
and assume that
![]() $0 \leq \tau , \theta \leq \pi $
. We have that
$0 \leq \tau , \theta \leq \pi $
. We have that
and let
![]() $a,b,c \in \{\pm 1\}$
be such that
$a,b,c \in \{\pm 1\}$
be such that
Theorem 7 of [Reference Conway and Jones8] gives that (A.3) is proportional to one of the following:
-
(a)
 $-\cos \delta +\cos (\frac {\pi }{3} - \delta ) + \cos (\frac {\pi }{3} + \delta ) = 0$
for some
$-\cos \delta +\cos (\frac {\pi }{3} - \delta ) + \cos (\frac {\pi }{3} + \delta ) = 0$
for some
 $0 < \delta < \frac {\pi }{6}$
;
$0 < \delta < \frac {\pi }{6}$
; -
(b)
 $\cos \frac {\pi }{7} - \cos \frac {2\pi }{7} + \cos \frac {3\pi }{7} = \frac {1}{2}$
;
$\cos \frac {\pi }{7} - \cos \frac {2\pi }{7} + \cos \frac {3\pi }{7} = \frac {1}{2}$
; -
(c)
 $\cos \frac {\pi }{5} - \cos \frac {\pi }{15} + \cos \frac {4\pi }{15} = \frac {1}{2}$
; and
$\cos \frac {\pi }{5} - \cos \frac {\pi }{15} + \cos \frac {4\pi }{15} = \frac {1}{2}$
; and -
(d)
 $-\cos \frac {2\pi }{5} + \cos \frac {2\pi }{15} - \cos \frac {7\pi }{15} = \frac {1}{2}$
.
$-\cos \frac {2\pi }{5} + \cos \frac {2\pi }{15} - \cos \frac {7\pi }{15} = \frac {1}{2}$
.
Observe that if (A.3) is proportional to either (c) or (d), then
![]() $5$
divides m. If (A.3) is proportional to (c), then we have that
$5$
divides m. If (A.3) is proportional to (c), then we have that
![]() $\theta = \frac {\pi }{3}$
,
$\theta = \frac {\pi }{3}$
,
![]() $\phi (\tau ) = \frac {\pi }{15}$
and
$\phi (\tau ) = \frac {\pi }{15}$
and
![]() $\{\phi (x), \phi (y) \} = \left \{\frac {4\pi }{15}, \frac {5\pi }{15}\right \}$
. We can see that there are no solutions for
$\{\phi (x), \phi (y) \} = \left \{\frac {4\pi }{15}, \frac {5\pi }{15}\right \}$
. We can see that there are no solutions for
![]() $x,y$
in this case. If (A.3) is proportional to (d), then we have that
$x,y$
in this case. If (A.3) is proportional to (d), then we have that
![]() $\theta = \frac {2\pi }{3}$
,
$\theta = \frac {2\pi }{3}$
,
![]() $\phi (\tau ) = \frac {2\pi }{15}$
and
$\phi (\tau ) = \frac {2\pi }{15}$
and
![]() $\{\phi (x), \phi (y) \} = \left \{\frac {6\pi }{15}, \frac {7\pi }{15}\right \}$
. There are also no solutions for
$\{\phi (x), \phi (y) \} = \left \{\frac {6\pi }{15}, \frac {7\pi }{15}\right \}$
. There are also no solutions for
![]() $x,y$
in this case.
$x,y$
in this case.
To finish Case (i), we will show that (A.3) cannot be proportional to either (a) or (b).
If (A.3) is proportional to (a), then
![]() $\cos \theta = 0$
and thus
$\cos \theta = 0$
and thus
![]() $\theta \in \left \{\frac {\pi }{2}, \frac {3\pi }{2}\right \}$
. We have three cases:
$\theta \in \left \{\frac {\pi }{2}, \frac {3\pi }{2}\right \}$
. We have three cases:
![]() $x+y = \frac {\pi }{2}$
,
$x+y = \frac {\pi }{2}$
,
![]() $y-x = \frac {\pi }{2}$
, or
$y-x = \frac {\pi }{2}$
, or
![]() $x+y = \frac {3\pi }{2}$
. If
$x+y = \frac {3\pi }{2}$
. If
![]() $\theta = x+y = \frac {\pi }{2}$
, then
$\theta = x+y = \frac {\pi }{2}$
, then
![]() $x\leq y \leq \frac {\pi }{2}$
so
$x\leq y \leq \frac {\pi }{2}$
so
![]() $\phi (z) = z$
for
$\phi (z) = z$
for
![]() $z \in \{x,y, y-x\}$
. Since (A.3) is proportional to (a),
$z \in \{x,y, y-x\}$
. Since (A.3) is proportional to (a),
![]() $\{x,y,y-x\} = \{\delta , \frac {\pi }{3} \pm \delta \}$
. If we sum all three elements, we obtain
$\{x,y,y-x\} = \{\delta , \frac {\pi }{3} \pm \delta \}$
. If we sum all three elements, we obtain
![]() $x+y + y -x =2y = \delta + \frac {2\pi }{3}$
and so
$x+y + y -x =2y = \delta + \frac {2\pi }{3}$
and so
![]() $y = \frac {\delta }{2} + \frac {\pi }{3} \notin \left \{\delta , \frac {\pi }{3} \pm \delta \right \}$
, a contradiction.
$y = \frac {\delta }{2} + \frac {\pi }{3} \notin \left \{\delta , \frac {\pi }{3} \pm \delta \right \}$
, a contradiction.
If
![]() $y-x = \theta = \frac {\pi }{2}$
, then
$y-x = \theta = \frac {\pi }{2}$
, then
![]() $x \leq \frac {\pi }{2} = \phi (x)$
. If
$x \leq \frac {\pi }{2} = \phi (x)$
. If
![]() $x = \delta $
, then
$x = \delta $
, then
![]() $y = \frac {\pi }{2} + \delta $
and
$y = \frac {\pi }{2} + \delta $
and
![]() $\phi (y) = \pi -y = \frac {\pi }{2} - \delta $
. We see that
$\phi (y) = \pi -y = \frac {\pi }{2} - \delta $
. We see that
![]() $\frac {\pi }{2} - \delta \neq \frac {\pi }{3} - \delta $
, so
$\frac {\pi }{2} - \delta \neq \frac {\pi }{3} - \delta $
, so
![]() $y = \frac {\pi }{3} + \delta = \frac {\pi }{2} - \delta $
. Then
$y = \frac {\pi }{3} + \delta = \frac {\pi }{2} - \delta $
. Then
![]() $x = \phi (x) = \frac {\pi }{12}$
. It follows that
$x = \phi (x) = \frac {\pi }{12}$
. It follows that
![]() $4|m$
, a contradiction. If
$4|m$
, a contradiction. If
![]() $x = \frac {\pi }{3} - \delta $
, then
$x = \frac {\pi }{3} - \delta $
, then
![]() $y = \frac {\pi }{2} + x = \frac {5\pi }{6} - \delta $
and
$y = \frac {\pi }{2} + x = \frac {5\pi }{6} - \delta $
and
![]() $\phi (y) = \pi -y = \frac {\pi }{6} + \delta \notin \left \{\delta , \frac {\pi }{3} + \delta \right \}$
, a contradiction. If
$\phi (y) = \pi -y = \frac {\pi }{6} + \delta \notin \left \{\delta , \frac {\pi }{3} + \delta \right \}$
, a contradiction. If
![]() $x = \frac {\pi }{3} + \delta $
, then
$x = \frac {\pi }{3} + \delta $
, then
![]() $y = \frac {\pi }{2} + x = \frac {5\pi }{6} + \delta $
and
$y = \frac {\pi }{2} + x = \frac {5\pi }{6} + \delta $
and
![]() $\phi (y) = \pi -y = \frac {\pi }{6} - \delta $
. Then
$\phi (y) = \pi -y = \frac {\pi }{6} - \delta $
. Then
![]() $\phi (y) = \delta $
and
$\phi (y) = \delta $
and
![]() $\delta = \frac {\pi }{12}$
. We obtain that
$\delta = \frac {\pi }{12}$
. We obtain that
![]() $x = \frac {5\pi }{12}$
and so
$x = \frac {5\pi }{12}$
and so
![]() $4|m$
, a contradiction.
$4|m$
, a contradiction.
If
![]() $x+y = \theta =\frac {3\pi }{2}$
, then
$x+y = \theta =\frac {3\pi }{2}$
, then
![]() $y = \frac {3\pi }{2} -x$
and
$y = \frac {3\pi }{2} -x$
and
![]() $\pi \geq x \geq \frac {\pi }{2}$
so
$\pi \geq x \geq \frac {\pi }{2}$
so
![]() $\phi (x) = \pi -x$
. See Table A.1 for all possible values of x, y, and
$\phi (x) = \pi -x$
. See Table A.1 for all possible values of x, y, and
![]() $y-x$
, based on the possible values of
$y-x$
, based on the possible values of
![]() $\phi (x)$
. If
$\phi (x)$
. If
![]() $\phi (x) = \frac {\pi }{3} + \delta $
, then
$\phi (x) = \frac {\pi }{3} + \delta $
, then
![]() $\phi (y) = \frac {\pi }{6} - \delta $
, which must equal
$\phi (y) = \frac {\pi }{6} - \delta $
, which must equal
![]() $\delta $
; hence,
$\delta $
; hence,
![]() $\delta = \frac {\pi }{12}$
and
$\delta = \frac {\pi }{12}$
and
![]() $y = \frac {13\pi }{12}$
and
$y = \frac {13\pi }{12}$
and
![]() $4|m$
, a contradiction. If
$4|m$
, a contradiction. If
![]() $\phi (x) = \frac {\pi }{3} - \delta $
, then
$\phi (x) = \frac {\pi }{3} - \delta $
, then
![]() $\phi (y) = \frac {\pi }{6} + \delta \notin \left \{\delta , \frac {\pi }{3} + \delta \right \}$
, a contradiction. If
$\phi (y) = \frac {\pi }{6} + \delta \notin \left \{\delta , \frac {\pi }{3} + \delta \right \}$
, a contradiction. If
![]() $\phi (x) = \delta $
, then
$\phi (x) = \delta $
, then
![]() $y-x = - \frac {\pi }{2} + 2\delta \geq 0$
, since
$y-x = - \frac {\pi }{2} + 2\delta \geq 0$
, since
![]() $y \geq x$
. But
$y \geq x$
. But
![]() $\delta \leq \frac {\pi }{6}$
, so this cannot happen.
$\delta \leq \frac {\pi }{6}$
, so this cannot happen.
Table A.1: Possible values of
![]() $\phi (x)$
.
$\phi (x)$
.
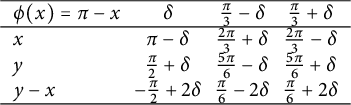
If (A.3) is proportional to (b), then
![]() $\cos \theta = \pm \frac {1}{2}$
and thus
$\cos \theta = \pm \frac {1}{2}$
and thus
![]() $\theta \in \left \{\frac {\pi }{3}, \frac {2\pi }{3},\frac {4\pi }{3},\frac {5\pi }{3}\right \}$
. Since
$\theta \in \left \{\frac {\pi }{3}, \frac {2\pi }{3},\frac {4\pi }{3},\frac {5\pi }{3}\right \}$
. Since
![]() $3$
and
$3$
and
![]() $7$
are prime, it is easy to see that any sum of two terms each of the form
$7$
are prime, it is easy to see that any sum of two terms each of the form
where
![]() $a, b \in {\mathbb Z}$
, will not be in the set
$a, b \in {\mathbb Z}$
, will not be in the set
![]() $\left \{\frac {\pi }{3}, \frac {2\pi }{3},\frac {4\pi }{3},\frac {5\pi }{3}\right \}$
. Thus, we cannot write
$\left \{\frac {\pi }{3}, \frac {2\pi }{3},\frac {4\pi }{3},\frac {5\pi }{3}\right \}$
. Thus, we cannot write
![]() $\theta $
as
$\theta $
as
![]() $x' +y'$
or
$x' +y'$
or
![]() $x'-y'$
for any
$x'-y'$
for any
![]() $x',y'$
pre-images under
$x',y'$
pre-images under
![]() $\phi $
of the arguments in (b), a contradiction.
$\phi $
of the arguments in (b), a contradiction.
Case (ii). In this case, two of the elements of C sum to a rational number, say
![]() $\cos \theta + \cos \tau $
. Then, applying Theorem 7 of [Reference Conway and Jones8] to
$\cos \theta + \cos \tau $
. Then, applying Theorem 7 of [Reference Conway and Jones8] to
![]() $a\cos (\phi (\theta )) + b\cos (\phi (\tau ))$
for
$a\cos (\phi (\theta )) + b\cos (\phi (\tau ))$
for
![]() $a,b \in \{\pm 1\}$
, we obtain that
$a,b \in \{\pm 1\}$
, we obtain that
Here,
![]() $5\mid m$
and we see again that the only additional solutions are the ones found in Lemma A.1.
$5\mid m$
and we see again that the only additional solutions are the ones found in Lemma A.1.
Case (iii). In this case, no proper subset C has rational sum. We have that
(for some choice of the signs). We apply Theorem 7 of [Reference Conway and Jones8] and see that this cannot hold, since all
![]() $4$
term sums in the theorem have nonzero sum. This completes the proof.
$4$
term sums in the theorem have nonzero sum. This completes the proof.
B Computation on regular maps
We looked at the regular maps as given in the census of Conder [Reference Conder6, Reference Conder7]. For each map, we considered the map and its dual, and determined their vertex truncations. We restricted our computation to bipartite regular maps on at least four vertices (since the two-vertex case is completely covered in Section 6.3) and with vertex (face) degree at least
![]() $3$
. Note that the underlying graph of the multigraph does not necessarily have degree at least 3. Up to and including regular maps with
$3$
. Note that the underlying graph of the multigraph does not necessarily have degree at least 3. Up to and including regular maps with
![]() $100$
edges, there are
$100$
edges, there are
![]() $351$
such regular maps. We determined the vertex truncations of these maps, as described in Section 5. Recall that the vertex truncation of a regular map with e edges is a vertex-transitive cubic graph on
$351$
such regular maps. We determined the vertex truncations of these maps, as described in Section 5. Recall that the vertex truncation of a regular map with e edges is a vertex-transitive cubic graph on
![]() $2e$
vertices that has
$2e$
vertices that has
![]() $1$
as an eigenvalue. Among the
$1$
as an eigenvalue. Among the
![]() $351$
considered vertex truncations of regular maps,
$351$
considered vertex truncations of regular maps,
![]() $62$
have
$62$
have
![]() $1$
as a simple eigenvalue. Their properties are listed in Table B.1.
$1$
as a simple eigenvalue. Their properties are listed in Table B.1.
Table B.1: Vertex truncations of regular maps which have
![]() $1$
as a simple eigenvalue. The first seven columns give information about the regular map. The last column records if the truncation obtained is bipartite.
$1$
as a simple eigenvalue. The first seven columns give information about the regular map. The last column records if the truncation obtained is bipartite.
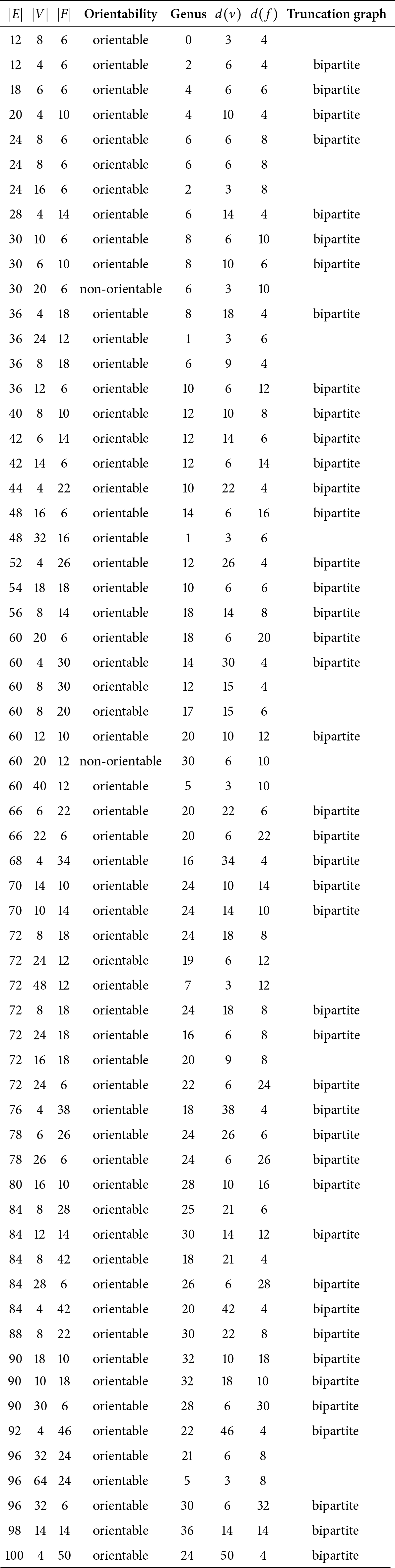
One can make some basic observations. The graphs of type
![]() $C(m,k)$
are obtained when k is the vertex degree of the regular map. From these examples, it looks that k is always even or divisible by 3. Of course, this could be the case because the graphs are too small and because we have excluded the two-vertex case (which gives the generalized Petersen graphs). Note that the two-vertex case includes
$C(m,k)$
are obtained when k is the vertex degree of the regular map. From these examples, it looks that k is always even or divisible by 3. Of course, this could be the case because the graphs are too small and because we have excluded the two-vertex case (which gives the generalized Petersen graphs). Note that the two-vertex case includes
![]() $k=5$
with two examples: the 5-prism (which has 1 as a simple eigenvalue) and the Petersen graph (where 1 is not simple). More generally, for every odd k, the k-prism has 1 as a simple eigenvalue. For
$k=5$
with two examples: the 5-prism (which has 1 as a simple eigenvalue) and the Petersen graph (where 1 is not simple). More generally, for every odd k, the k-prism has 1 as a simple eigenvalue. For
![]() $k=3$
, there are infinitely many examples of type
$k=3$
, there are infinitely many examples of type
![]() $C(\cdot ,3)$
(see Section 6.2), but it is not known whether there are infinitely many examples of type
$C(\cdot ,3)$
(see Section 6.2), but it is not known whether there are infinitely many examples of type
![]() $C(\cdot ,k)$
for any other k.
$C(\cdot ,k)$
for any other k.