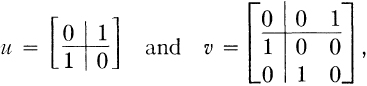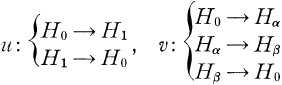Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ichihara, Ryo
1980.
A remark concerning the extensions of some group $C^\ast$-algebras.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 56,
Issue. 9,
Avitzour, Daniel
1982.
Free products of 𝐶*-algebras.
Transactions of the American Mathematical Society,
Vol. 271,
Issue. 2,
p.
423.
Lee, Tan-Yu
1983.
Embedding Theorems in Group C*-Algebras†.
Canadian Mathematical Bulletin,
Vol. 26,
Issue. 2,
p.
157.
Bédos, Erik
1984.
Operator algebras associated with free products of groups with amalgamation.
Mathematische Annalen,
Vol. 266,
Issue. 3,
p.
279.
Voiculescu, Dan
1985.
Operator Algebras and their Connections with Topology and Ergodic Theory.
Vol. 1132,
Issue. ,
p.
556.
Archbold, R.J
and
Batty, C.J.K
1985.
Extensions of factorial states of C∗-algebras.
Journal of Functional Analysis,
Vol. 63,
Issue. 1,
p.
86.
Archbold, R. J.
and
Kumjian, Alexander
1986.
Nuclear subalgebras of UHF C*-algebras.
Proceedings of the Edinburgh Mathematical Society,
Vol. 29,
Issue. 1,
p.
97.
Balogun, Bola O.
1987.
C*-algebras associated with amalgamated products of groups.
Glasgow Mathematical Journal,
Vol. 29,
Issue. 2,
p.
143.
Shtern, A. I.
1987.
Nuclear C*-algebras and related questions.
Journal of Soviet Mathematics,
Vol. 38,
Issue. 2,
p.
1762.
Lazar, Aldo
Tsui, Sze-Kai
and
Wright, Stephen
1988.
Pure state extensions of the trace on the Choi algebra.
Proceedings of the American Mathematical Society,
Vol. 102,
Issue. 4,
p.
957.
Spielberg, John S.
1988.
Embedding C∗-algebra extensions into AF algebras.
Journal of Functional Analysis,
Vol. 81,
Issue. 2,
p.
325.
Archbold, Robert
Lazar, Aldo
Tsui, Sze-Kai
and
Wright, Stephen
1991.
Factor state extensions of type III.
Journal of Functional Analysis,
Vol. 95,
Issue. 1,
p.
219.
Kraus, Jon
1991.
The slice map problem and approximation properties.
Journal of Functional Analysis,
Vol. 102,
Issue. 1,
p.
116.
Zhang, Shuang
1992.
CertainC*-algebras with real rank zero and their corona and multiplier algebras: II.
K-Theory,
Vol. 6,
Issue. 1,
p.
1.
Stacey, P. J.
1992.
A family of type 𝐼𝐼𝐼 extensions of the trace on the Choi algebra.
Proceedings of the American Mathematical Society,
Vol. 114,
Issue. 3,
p.
683.
Spielberg, J. S.
1993.
Cuntz—Krieger algebras associated with Fuchsian groups.
Ergodic Theory and Dynamical Systems,
Vol. 13,
Issue. 3,
p.
581.
Kaplan, Alexander
1993.
Covariant Completely Positive Maps and Liftings.
Rocky Mountain Journal of Mathematics,
Vol. 23,
Issue. 3,
McClanahan, Kevin
1994.
Simplicity Of Reduced Amalgamated Products of C*-Algebras.
Canadian Journal of Mathematics,
Vol. 46,
Issue. 4,
p.
793.
Wassermann, Simon
1994.
Subquotients of UHF C*-algebras.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 115,
Issue. 3,
p.
489.
Murphy, G.
and
Phillips, N.
1996.
𝐶*-Algebras with the Approximate Positive Factorization Property.
Transactions of the American Mathematical Society,
Vol. 348,
Issue. 6,
p.
2291.