Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T09:33:25.462Z Has data issue: false hasContentIssue false
  • English
  • Français

Sharp Localized Inequalities for Fourier Multipliers

Published online by Cambridge University Press:  20 November 2018

Adam Osękowski
Adam Osękowski*
Affiliation:
Department of Mathematics, Informatics and Mechanics, Warsaw University, Banacha 2, 02-097 Warsaw, Poland. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study sharp localized 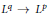${{L}^{q}}\,\to \,{{L}^{p}}$ estimates for Fourier multipliers resulting from modulation of the jumps of Lévy processes. The proofs of these estimates rest on probabilistic methods and exploit related sharp bounds for differentially subordinated martingales, which are of independent interest. The lower bounds for the constants involve the analysis of laminates, a family of certain special probability measures on 2×2 matrices. As an application, we obtain new sharp bounds for the real and imaginary parts of the Beurling–Ahlfors operator.

Keywords

42B1560G4442B20Fourier multipliermartingalelaminate
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 6 , 01 December 2014 , pp. 1358 - 1381
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Astala, K., Faraco, D., and Székelyhidi, L., Jr., Convex integration and the Lp theory of elliptic equations. Ann. Sci. Norm. Super. Pisa Cl. Sci. (5) 7(2008), 1–50.Google Scholar
[2] Astala, K., Iwaniec, T., and Martin, G., Elliptic Partial Differential Equations and Quasiconformal Mappings in the Plane. Princeton University Press, Princeton, NJ, 2008.Google Scholar
[3] Ba˜ñuelos, R., The foundational inequalities of D. L. Burkholder and some of their ramifications. Illinois J. Math. 54(2010), 789–868.Google Scholar
[4] Ba˜ñuelos, R. and Bogdan, K., Lévy processes and Fourier multipliers. J. Funct. Anal. 250(2007), 197–213.http://dx.doi.org/10.1016/j.jfa.2007.05.013 Google Scholar
[5] Ba˜ñuelos, R., Bielaszewski, A., and Bogdan, K., Fourier multipliers for non-symmetric Lévy processes. In: Marcinkiewicz centenary volume, Banach Center Publ. 95, Polish Acad. Sci. Inst. Math., Warsaw, 2011, 9–25.Google Scholar
[6] Ba˜ñuelos, R. and Osękowski, A., Martingales and sharp bounds for Fourier multipliers. Ann. Acad. Sci.Fenn. Math. 37(2012), 251–263.http://dx.doi.org/10.5186/aasfm.2012.3710 Google Scholar
[7] Bañuelos;, R.˜ and Wang, G., Sharp inequalities for martingales with applications to the Beurling-Ahlfors. and Riesz transformations. Duke Math. J. 80(1995), 575–600.http://dx.doi.org/10.1215/S0012-7094-95-08020-X Google Scholar
[8] Boros, N., Székelyhidi, L. Jr., and Volberg, A., Laminates meet Burkholder functions. J. Math. Pures Appl. 100(2013), 687-700.http://dx.doi.org/10.1016/j.matpur.2013.01.017 Google Scholar
[9] Burkholder, D. L., Boundary value problems and sharp inequalities for martingale transforms. Ann. Probab. 12(1984), 647–702.http://dx.doi.org/10.1214/aop/1176993220 Google Scholar
[10] Burkholder, D. L., A Sharp and Strict Lp-Inequality for Stochastic Integrals. Ann. Probab. 15(1987), 268–273.http://dx.doi.org/10.1214/aop/1176992268 Google Scholar
[11] Burkholder, D. L., A proof of Pełczyński's conjecture for the Haar system. Studia Math. 91(1988), 79–83.Google Scholar
[12] Burkholder, D. L., Strong differential subordination and stochastic integration. Ann. Probab. 22(1994), 995–1025.http://dx.doi.org/10.1214/aop/1176988738 Google Scholar
[13] Choi, C., A submartingale inequality. Proc. Amer. Math. Soc. 124(1996), 2549–2553.http://dx.doi.org/10.1090/S0002-9939-96-03617-9 Google Scholar
[14] Choi, K. P., A sharp inequality for martingale transforms and the unconditional basis constant of a monotone basis in Lp.(0; 1). Trans. Amer. Math. Soc. 330(1992), 509–529.Google Scholar
[15] Conti, S., Faraco, D., and Maggi, F., A new approach to counterexamples to L1estimates: Korn’s.inequality, geometric rigidity, and regularity for gradients of separately convex functions. Arch. Rat. Mech. Anal. 175(2005), 287–300.http://dx.doi.org/10.1007/s00205-004-0350-5 Google Scholar
[16] Dellacherie, C. and Meyer, P.-A., Probabilities and potential B: Theory of martingales. North Holland, Amsterdam, 1982.Google Scholar
[17] Geiss, E., Montgomery-Smith, S., and Saksman, E., On singular integral and martingale transforms. Trans. Amer. Math. Soc. 362(2010), 553–575.http://dx.doi.org/10.1090/S0002-9947-09-04953-8 Google Scholar
[18] Hammack, W., Sharp inequalities for the distribution of a stochastic integral in which the integrator is a. bounded submartingale. Ann. Probab. 23(1995), 223–235.http://dx.doi.org/10.1214/aop/1176988384 Google Scholar
[19] Hörmander, L., Estimates for translation invariant operators in Lp spaces. Acta Math. 104(1960),93–140.http://dx.doi.org/10.1007/BF02547187 Google Scholar
[20] Kirchheim, B., Rigidity and Geometry of Microstructures. Habilitation Thesis, University of Leipzig, 2003.http://www.mis.mpg.de/publications/other-series/ln/lecturenote-1603.html Google Scholar
[21] Kirchheim, B., Müller, S., and Šverák, V., Studying nonlinear pde by geometry in matrix space. In:Geometric Analysis and nonlinear partial differential equations, Springer, Berlin, 2003, 347–395.Google Scholar
[22] Kurtz, D. S., Littlewood-Paley and multiplier theorems on weighted Lp spaces. Trans. Amer. Math. Soc. 259(1980), 235–254.Google Scholar
[23] Kurtz, D. S. and L.Wheeden, R., Results on weighted norm inequalities for multipliers. Trans. Amer. Math. Soc. 255(1979), 343–362.http://dx.doi.org/10.1090/S0002-9947-1979-0542885-8 Google Scholar
[24] McConnell, T. R., On Fourier multiplier transformations of Banach-valued functions. Trans. Amer. Math. Soc. 285(1984), 739–757.http://dx.doi.org/10.1090/S0002-9947-1984-0752501-X Google Scholar
[25] Mihlin, S. G., On the multipliers of Fourier integrals. (Russian) Dokl. Akad. Nauk SSSR (N.S.) 109(1956), 701–703.Google Scholar
[26] Müller, S. and Šverák, V., Convex integration for Lipschitz mappings and counterexamples to regularity.. Ann. of Math. (2) 157(2003), 715–742.http://dx.doi.org/10.4007/annals.2003.157.715 Google Scholar
[27] Osękowski, A., Sharp moment inequalities for differentially subordinated martingales. Studia Math. 201(2010), 103–131.http://dx.doi.org/10.4064/sm201-2-1 Google Scholar
[28] Osękowski, A., On relaxing the assumption of differential subordination in some martingale inequalities. Electron. Commun. Probab. 15(2011), 9–21.Google Scholar
[29] Osękowski, A., Sharp martingale and semimartingale inequalities. IMPAN Monogr. Mat. (N.S.) 72, Birkhäuser, Basel, 2012.Google Scholar
[30] Osękowski, A., Logarithmic inequalities for Fourier multipliers. Math. Z. 274(2013), 515–530.http://dx.doi.org/10.1007/s00209-012-1083-z Google Scholar
[31] Osękowski, A., Weak-type inequalities for Fourier multipliers with applications to the Beurling-Ahlfors transform.. Math. Soc. Japan, to appear.Google Scholar
[32] Székelyhidi, L. Jr., Counterexamples to elliptic regularity and convex integration. Contemp. Math. 424(2007), 227–245.Google Scholar
[33] Suh, Y., A sharp weak type (p,p) inequality (p > 2) for martingale transforms and other subordinate martingales. Trans. Amer. Math. Soc. 357(2005), 1545–1564.http://dx.doi.org/10.1090/S0002-9947-04-03563-9 +2)+for+martingale+transforms+and+other+subordinate+martingales.+Trans.+Amer.+Math.+Soc.+357(2005),+1545–1564.http://dx.doi.org/10.1090/S0002-9947-04-03563-9>Google Scholar
[34] Wang, G., Differential subordination and strong differential subordination for continuous time martingales and related sharp inequalities Ann. Probab. 23(1995), 522–551.http://dx.doi.org/10.1214/aop/1176988278 Google Scholar