Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-11T06:05:58.678Z Has data issue: false hasContentIssue false
  • English
  • Français

Sharp endpoint estimates for some operators associated with the Laplacian with drift in Euclidean space

Part of: Harmonic analysis in several variables Partial differential equations on manifolds; differential operators

Published online by Cambridge University Press:  16 June 2020

Hong-Quan Li  and
Peter Sjögren
Hong-Quan Li
Affiliation:
School of Mathematical Sciences, Fudan University, 220 Handan Road, Shanghai200433, People’s Republic of China e-mail: [email protected][email protected]
Peter Sjögren*
Affiliation:
Mathematical Sciences, University of Gothenburg, and Mathematical Sciences, Chalmers, SE-412 96Göteborg, Sweden
*
e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

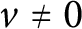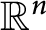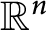Let $v \ne 0$ be a vector in ${\mathbb {R}}^n$ . Consider the Laplacian on ${\mathbb {R}}^n$ with drift 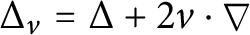$\Delta _{v} = \Delta + 2v\cdot \nabla $ and the measure 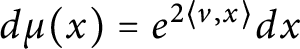$d\mu (x) = e^{2 \langle v, x \rangle } dx$ , with respect to which 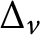$\Delta _{v}$ is self-adjoint. This measure has exponential growth with respect to the Euclidean distance. We study weak type 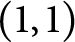$(1, 1)$ and other sharp endpoint estimates for the Riesz transforms of any order, and also for the vertical and horizontal Littlewood–Paley–Stein functions associated with the heat and the Poisson semigroups.

Keywords

Riesz transformLittlewood–Paley–Stein operatorsHeat semigroupLaplacian with drift

MSC classification

Primary: 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.)
Secondary: 42B25: Maximal functions, Littlewood-Paley theory 58J35: Heat and other parabolic equation methods
Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 5 , October 2021 , pp. 1278 - 1304
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Canadian Mathematical Society 2020

Footnotes

H.-Q. Li is partially supported by NSF of China (Grants No. 11625102 and No. 11571077) and The Program of Shanghai Academic Research Leader (18XD1400700). Both authors profited from a grant from the Gothenburg Centre for Advanced Studies in Science and Technology.

References

Alexopoulos, G., An application of homogenization theory to harmonic analysis: Harnack inequalities and Riesz transforms on Lie groups of polynomial growth . Canad. J. Math. 44(1992), 691–727. http://dx.doi.org/10.4153/CJM-1992-042-x CrossRefGoogle Scholar
Andersson, A. and Sjögren, P., Ornstein-Uhlenbeck theory in finite dimension . Lecture Notes Dept. Math. Sciences, University of Gothenburg, Chalmers, 2012.Google Scholar
Anker, J.-P., Sharp estimates for some functions of the Laplacian on noncompact symmetric spaces . Duke Math. J. 65(1992), 257–297. http://dx.doi.org/10.1215/S0012-7094-92-06511-2 CrossRefGoogle Scholar
Anker, J.-P., Damek, E., and Yacoub, C., Spherical analysis on harmonic AN groups. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 23(1996), 643–679.Google Scholar
Auscher, P., Coulhon, T., Duong, X.-T., and Hofmann, S., Riesz transform on manifolds and heat kernel regularity . Ann. Sci. École Norm. Sup. (4) 37(2004), 911–957. http://dx.doi.org/10.1016/j.ansens.2004.10.003 CrossRefGoogle Scholar
Bakry, D., Étude des transformations de Riesz dans les variétés riemanniennes à courbure de Ricci minorée. In: Séminaire de Probabilités XXI, Lecture Notes in Math., 1247, Springer, Berlin, 1987, pp. 137–172. http://dx.doi.org/10.1007/BFb0077631 Google Scholar
Carron, G., Coulhon, T., and Hassell, A., Riesz transform and ${L}^p$ -cohomology for manifolds with Euclidean ends . Duke Math. J. 133(2006), 59–93. http://dx.doi.org/10.1215/S0012-7094-06-13313-6 CrossRefGoogle Scholar
Chen, L., Coulhon, T., Feneuil, J., and Russ, E., Riesz transform for $1\le p\le 2$ without Gaussian heat kernel bound . J. Geom. Anal. 27(2017), 1489–1514. http://dx.doi.org/10.1007/s12220-016-9728-5 CrossRefGoogle Scholar
Coulhon, T. and Duong, X. T., Riesz transforms for $1\le p\le 2$ . Trans. Amer. Math. Soc. 351(1999) 1151–1169. http://dx.doi.org/10.1090/S0002-9947-99-02090-5 CrossRefGoogle Scholar
Coulhon, T., Duong, X.-T., and Li, X.-D., Littlewood-Paley-Stein functions on complete Riemannian manifolds for $1\le p\le 2$ . Studia Math. 154(2003), 37–57. http://dx.doi.org/10.4064/sm154-1-4 CrossRefGoogle Scholar
Coulhon, T. and Li, H.-Q., Estimations inférieures du noyau de la chaleur sur les variétés coniques et transformée de Riesz . Arch. Math. 83(2004), 229–242. http://dx.doi.org/10.1007/s00013-004-1029-8 CrossRefGoogle Scholar
Elst, A. F. M., Robinson, D. W., and Sikora, A., Riesz transforms and Lie groups of polynomial growth. J. Funct. Anal. 162(1999), 14–51. http://dx.doi.org/10.1006/jfan.1998.3361CrossRefGoogle Scholar
Fabes, E. B., Gutiérrez, C. E., and Scotto, R., Weak-type estimates for the Riesz transforms associated with the Gaussian measure . Rev. Mat. Iberoamericana 10(1994), 229–281. http://dx.doi.org/10.4171/RMI/152 CrossRefGoogle Scholar
Gaudry, G. I., Qian, T., and Sjögren, P., Singular integrals associated to the Laplacian on the affine group $ax + b$ . Ark. Math. 30(1992), 259–281. http://dx.doi.org/10.1007/BF02384874 CrossRefGoogle Scholar
Gradshteyn, I. S. and Ryzhik, I. M., Table of integrals, series, and products. 7th ed. Translation edited and with a preface by Jeffrey, Alan and Zwillinger, Daniel. Academic Press, Inc., San Diego, CA, 2007.Google Scholar
Grigor’yan, A., Heat kernel and analysis on manifolds . AMS/IP Studies in Advanced Mathematics, 47, American Mathematical Society, Providence, RI, International Press, Boston, MA, 2009. http://dx.doi.org/10.1090/amsip/047 Google Scholar
Hebisch, W. and Steger, T., Multipliers and singular integrals on exponential growth groups . Math. Z. 245(2003), 37–61. http://dx.doi.org/10.1007/s00209-003-0510-6 CrossRefGoogle Scholar
Li, H.-Q, La transformation de Riesz sur les variétés coniques . J. Funct. Anal. 168(1999), 145–238. http://dx.doi.org/10.1006/jfan.1999.3464 CrossRefGoogle Scholar
Li, H.-Q. and Sjögren, P., Weak type $(1,1)$ for some operators related to the Laplacian with drift on real hyperbolic spaces. Potential Anal. 46(2017), 463–484. http://dx.doi.org/10.1007/s11118-016-9590-x CrossRefGoogle Scholar
Li, H.-Q., Sjögren, P., and Wu, Y.-R., Weak type $(1,1)$ of some operators for the Laplacian with drift . Math. Z. 282(2016), 623–633. http://dx.doi.org/10.1007/s00209-015-1555-z CrossRefGoogle Scholar
Li, H.-Q. and Zhu, J.-X., A note on “Riesz transform for $1\le p\le 2$ without Gaussian heat kernel bound”. J. Geom. Anal. 28(2018), 1597–1609. http://dx.doi.org/10.1007/s12220-017-9879-z CrossRefGoogle Scholar
Lohoué, N., Comparaison des champs de vecteurs et des puissances du laplacien sur une variété riemannienne à courbure non positive . J. Funct. Anal. 61(1985), 164–201. http://dx.doi.org/10.1016/0022-1236(85)90033-3 CrossRefGoogle Scholar
Lohoué, N., Estimation des fonctions de Littlewood-Paley-Stein sur les variétés riemanniennes à courbure non positive . Ann. Sci. École Norm. Sup. 20(1987), 505–544.CrossRefGoogle Scholar
Lohoué, N., Transformées de Riesz et fonctions sommables . Amer. J. Math. 114(1992), 875–922. http://dx.doi.org/10.2307/2374800 CrossRefGoogle Scholar
Lohoué, N. and Mustapha, S., Sur les transformées de Riesz sur les espaces homogènes des groupes de Lie semi-simples . Bull. Soc. Math. France 128(2000), 485–495.CrossRefGoogle Scholar
Lohoué, N. and Mustapha, S., Sur les transformées de Riesz dans le cas du Laplacien avec drift . Trans. Amer. Math. Soc. 356(2004), 2139–2147. http://dx.doi.org/10.1090/S0002-9947-04-03159-9 CrossRefGoogle Scholar
Pérez, S. and Soria, F., Operators associated with the Ornstein-Uhlenbeck semigroup. J. Lond. Math. Soc. (2) 61(2000), 857–871. http://dx.doi.org/10.1112/S0024610700008917 CrossRefGoogle Scholar
Sjögren, P. and Vallarino, M., Boundedness from ${H}^1$ to ${L}^1$ of Riesz transforms on a Lie group of exponential growth . Ann. Inst. Fourier 58(2008), 1117–1151.CrossRefGoogle Scholar
Stein, E. M., Topics in harmonic analysis related to the Littlewood-Paley theory. Annals of Mathematics Studies, 63, Princeton University Press, Princeton, NJ, 1970.Google Scholar
Stein, E. M. and Weiss, N. J., On the convergence of Poisson integrals . Trans. Amer. Math. Soc. 140(1969), 35–54. http://dx.doi.org/10.2307/1995121 CrossRefGoogle Scholar