Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nakazi, Takahiko
2011.
Szegö's Theorem and Uniform Algebras.
Canadian Mathematical Bulletin,
Vol. 54,
Issue. 2,
p.
338.
Lu, Yu Feng
Hu, Yin Yin
and
Liu, Liu
2015.
Compact Toeplitz operators on the weighted Dirichlet space.
Acta Mathematica Sinica, English Series,
Vol. 31,
Issue. 1,
p.
35.


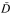 . For each a in
. For each a in