Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T00:53:05.100Z Has data issue: false hasContentIssue false
  • English
  • Français

Relations Between Mahler's Measure and Values of L-Series

Published online by Cambridge University Press:  20 November 2018

Gary Alan Ray
Gary Alan Ray*
Affiliation:
University of British Columbia, Vancouver, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Mahler's measure is a natural generalization of Jensen's formula to polynomials in several variables. Its definition is as follows:

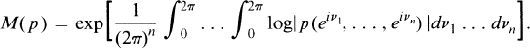
The importance of Mahler's measure for polynomials in several variables lies in its connection to Lehmer's classical question which can be phrased in terms of Mahler's measure for polynomials in one variable:

Given 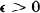, are there any polynomials p with integer coefficients in one variable for which ?

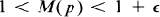Surprisingly, Boyd [1] has shown that to answer this question, it is necessary to investigate the larger question involving polynomials in several variables.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 3 , 01 June 1987 , pp. 694 - 732
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Boyd, D. W., Speculations concerning the range of Mahler's measure, Canad. Math. Bull. 24 (1981), 453–469.Google Scholar
2. Chinburg, T., Mahler measures and derivatives of L-functions at non-positive integers, (in preparation).Google Scholar
3. Lewin, L., Poly logarithms and associated functions (North Holland, 1981).Google Scholar
4. Lojasiewicz, S., Ensembles semi-analytiques (Institut des hautes etudes scientifiques, Paris, 1964).Google Scholar
5. Marcus, D., Number fields (Springer-Verlag, 1977).CrossRefGoogle Scholar
6. Milnor, J., On poly logarithms, Hurwitz zeta functions, and the Kubert identities, L'Enseignement Mathématique 29 (1983), 281–322.Google Scholar
7. Rogers, L.J., On function sum theorems connected with the series , Proc. London Math. Soc. 4 (1907), 169–189.Google Scholar
8. Sandham, H. F., A logarithmic trancendent, Jour. London Math. Soc. 24 (1949), 83–91.Google Scholar
9. Smyth, C. J., On measures of polynomials in several variables, Bull. Austral. Math. Soc. 23 (1981), 49–63.Google Scholar
10. Washington, L., Cyclotomic fields (Springer-Verlag, 1983).Google Scholar