Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T13:33:04.403Z Has data issue: false hasContentIssue false
  • English
  • Français

Regular Neighborhoods of Immersed Manifolds

Published online by Cambridge University Press:  20 November 2018

J. W. Maxwell
J. W. Maxwell*
Affiliation:
Oklahoma State University, Stillwater, Oklahoma
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

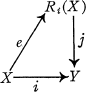
Let X and Y denote polyhedra, i : X → Y a PL immersion. A regular neighborhood of X associated with i is a regular neighborhood (e, Ri(X)) of X together with an immersion j : Ri(X) → Y

such that the diagram.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 6 , December 1974 , pp. 1480 - 1483
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Haefliger, A. and Poenaru, V., La classification des Immersions combinatories, Pubis. Math. Inst. Ht. Etud. Scient. No. 23 (1964), 75–91.Google Scholar
2. Hirsch, M. W., On tubular neighborhoods of piecewise linear and topological manifolds, in Conference on the topology of manifolds (Edited by John G. Hocking; Prindle, Weber, and Schmidt, Inc., Boston, 1968).Google Scholar
3. Hudson, J. F. P., Piecewise linear topology (W. A. Benjamin, New York, 1969).Google Scholar
4. Hudson, J. F. P., Knotted tori, Topology 2 (1963), 11–23.Google Scholar
5. Husemoller, D., Fibre bundles (McGraw-Hill, New York, 1966).Google Scholar
6. Ivansic, I., Improper embeddings and unknotting of P.L. manifolds, Michigan Math. J. 19 (1972), 33–44.Google Scholar
7. Lickorish, W. B. R. and Siebenmann, L. C., Regular neighborhoods and the stable range, Trans. Amer. Math. Soc. 139 (1969), 207–230.Google Scholar
8. Maxwell, J. W., Obstructions to embedding n-manifolds in (2n-l)-manifolds, Trans. Amer. Math. Soc. 181 (1973), 423–435.Google Scholar
9. Rourke, C. P. and Sanderson, B. J., Block bundles: I, III, Ann. of Math. 87 (1968), 1–28; 431-483.Google Scholar
10. Smith, A., Piecewise linear immersions, Proc. Cambridge Philos. Soc. 68 (1970), 45–55.Google Scholar
11. Zeeman, E. C., Seminar on combinatorial topology, I.H.E.S. Paris 1963 (1966), mimeographed notes.Google Scholar