Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T01:07:53.566Z Has data issue: false hasContentIssue false
  • English
  • Français

Pure Compactifications in Quasi-Primal Varieties

Published online by Cambridge University Press:  20 November 2018

Walter Taylor
Walter Taylor*
Affiliation:
University of Colorado, Boulder, Colorado
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

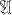We prove that is quasi-primal, then every algebra in HSP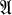has a pure embedding into a product of finite algebras. For a general theory of varieties 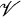for which every 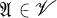can be purely embedded in an equationally compact algebra 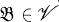, and for all notions not explained here, the reader is referred to [38; 6; or 5]. This theorem was known for Boolean algebras simply as a corollary of the Stone representation theorem and the fact that in the variety of Boolean algebras, all embeddings are pure [2].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 28 , Issue 1 , 01 February 1976 , pp. 50 - 62
Copyright
Copyright © Canadian Mathematical Society 1976

References

1. Ash, C. J., On countable n-valued Post algebras, Algebra Universalis 2 (1972), 339–345.Google Scholar
2. Bacsich, P. D., Injectivity in model theory, Colloq. Math. 25 (1972), 165–176.Google Scholar
3. Banaschewski, B., Injectivity and essential extensions in equational classes of algebras, Queen's papers 25 (1970), 131–147.Google Scholar
4. Banaschewski, B., Equational compactness of G-sets, Can. Math. Bull. 17 (1974), 11–18.Google Scholar
5. Banaschewski, B., Equational compactness in universal algebra, manuscript, Prague and Hamilton, 1973.Google Scholar
6. Banaschewski, B. and Nelson, E., Equational compactness in equational classes of algebras, Algebra Universalis 2 (1972), 152–165.Google Scholar
7. Beazer, R., Post-like algebras and infective Stone algebras, Algebra Universalis 5 (1975), 16–23.Google Scholar
8. Beazer, R., Compactness in abstractions of Post algebras, Notre Dame J. Formal Logic 16 (1975), 389–396.Google Scholar
9. Bernardi, C., Su alcuni condizioni necessarie per Vindipendenza di due varietà di algèbre, Boll. Un. Mat. Ital. 6 (1972), 410–421.Google Scholar
10. Birkhoff, G., Subdirect unions in universal algebra, Bull. Amer. Math. Soc. 50 (1944), 764–768.Google Scholar
11. Burris, S., Subdirect representations in axiomatic classes, ms., Waterl∞, Ontario, 1973.Google Scholar
12. Day, A., Injectivity in equational classes of algebras, Can. J. Math. 24 (1972), 209–220.Google Scholar
13. Draskovicovâ, H., Independence of equational classes, Mat. Casopis, Sloven. Akad. Vied 23 (1973), 125–135.Google Scholar
14. Gerhard, J. A., The lattice of equational classes of idempotent semigroups, J. Algebra 15 (1970), 195–224.Google Scholar
15. Gerhard, J. A., Subdirectly irreducible idempotent semigroups, Pacific J. Math. 39 (1971), 669–676.Google Scholar
16. Grâtzer, G., Lattice theory (H. M. Freeman, San Francisco, 1971).Google Scholar
17. Grâtzer, G., Lakser, H. and Pionka, J., Joins and direct products of equational classes, Can. Math. Bull. 12 (1969), 741–744.Google Scholar
18. Hu, T.-K., Characterization of algebraic functions in equational classes generated by independent primal algebras, Algebra Universalis 1 (1971), 187–191.Google Scholar
19. Hu, T.-K. and Kelenson, P., Independence and direct factorization of universal algebras, Math. Nachr. 51 (1971), 83–99.Google Scholar
20. Jones, J. T., Pseudocomplemented semilattices, Ph.D. thesis, U.C.L.A., 1972.Google Scholar
21. Jônsson, B., Algebras whose congruence lattices are distributive, Math. Scand. 21 (1967), 110–121.Google Scholar
22. Kalman, J. A., Equational completeness and families of sets closed under subtraction, Indag. Math. 22 (1960), 402–405.Google Scholar
23. Katrinâk, T., The structure of distributive double p-algebras, Algebra Universalis 3 (1973), 238–246.Google Scholar
24. Lakser, H., Infective completeness of varieties of unary algebras: a remark on a paper of Higgs, Algebra Universalis 3 (1973), 129–130.Google Scholar
25. Lausch, H., and W., Nöbauer, Algebra of polynomials (North-Holland, Amsterdam, 1973).Google Scholar
26. Los, J., Abelian groups that are direct summands of any Abelian group which contains them as pure subgroups, Fund. Math. 44 (1957), 84–90.Google Scholar
27. Lyndon, R. C., Identities in two-valued calculi, Trans. Amer. Math. Soc. 71 (1951), 457–465.Google Scholar
28. Mitschke, A., Implication algebras are 3-permutable and 3-distributive, Algebra Universalis 1 (1971), 182–186.Google Scholar
29. Monk, D., On equational classes of algebraic versions of logic I, Math. Scand. 27 (1970), 53–71.Google Scholar
30. Mycielski, J., Some compactifications of general algebras, Colloq. Math. 13 (1964), 1–9.Google Scholar
31. Nelson, E., Semilattices do not have equationally compact hulls, ms., Hamilton, Ontario, 1974.Google Scholar
32. Pixley, A. F., Functionally complete algebras generating distributive and permutable classes, Math. Z. 114 (1970), 361–372.Google Scholar
33. Pixley, A. F., The ternary discriminator function in universal algebra, Math. Ann. 191 (1971), 167–180.Google Scholar
34. Post, E. L., Introduction to the general theory of elementary propositions, Amer. J. Math. 43 (1921), 163–185.Google Scholar
35. Quackenbush, R. W., Demi-semi-primal algebras and MaVcev-type conditions, Math. Z. 122 (1971), 166–176.Google Scholar
36. Quackenbush, R. W., Structure theory for equational classes generated by quasi-primal algebras, Trans. Amer. Math. Soc. 187 (1974), 127–145.Google Scholar
37. Sankappanavar, H. P., A study of congruence lattices of pseudo-complemented semilattices, Ph.D. thesis, Waterl∞, 1974.Google Scholar
38. Taylor, W., Residually small varieties, Algebra Universalis 2 (1972), 33–53.Google Scholar
39. Taylor, W., Products of absolute retracts, Algebra Universalis 3 (1973), 400–401.Google Scholar
40. Taylor, W., Pure-irreducible mono-unary algebras, Algebra Universalis 4 (1974), 235–243.Google Scholar
41. Taylor, W., The fine spectrum of a variety, to appear, Algebra Universalis.Google Scholar
42. Traczyk, T., An equational definition of a class of Post algebras, Bull. Pol. Acad. Sci. 12 (1964), 147–149.Google Scholar
43. Varlet, J., A regular variety of type (2, 2, 1, 1, 0, 0 ), Algebra Universalis 2 (1972), 218–223.Google Scholar
44. Banaschewski, B. and Nelson, E., B∞lean powers as algebras of continuous functions, Mimeographed, Hamilton, 1975.Google Scholar
45. Bulman-Fleming, S. and Werner, H., Equational compactness in quasi-primal varieties, Abstract 75T-A139, Notices Amer. Math. Soc. 22 (1975), A-448.Google Scholar
46. Hule, H. and Miiller, W. B., On the compatibility of algebraic equations with extensions, to appear.Google Scholar
47. Keimel, K. and Werner, H., Stone duality for varieties generated by quasi-primal algebras, Memoirs Amer. Math. Soc. 1-8 (1974), 59–85.Google Scholar
48. Macdonald, S. O. and Street, A. P., On laws in linear groups, Quart. J. Math. Oxford (2) 23 (1972), 1–12.Google Scholar
49. Neumann, H., Varieties of groups, Ergebnisse der Math., vol. 37 (Springer-Verlag, Berlin, 1967).Google Scholar
50. Ol'shanski, A. Ju., Varieties of finitely approximable groups, (Russian) Izv. Akad. Nauk S.S.S.R. Ser. Mat. 33 (1969), 915–927.Google Scholar