1 Introduction
Trisections of oriented compact 4-manifolds were introduced by Gay and Kirby in [Reference Gay and Kirby7], who established existence and uniqueness in the closed setting. In the relative setting—that is, for oriented compact 4-manifolds with boundary—a relative trisection induces an open book decomposition on the boundary. Gay and Kirby show existence of relative trisections inducing any given open book on the boundary, and uniqueness (up to stabilization) given a fixed open book on the boundary. This uniqueness result was improved in Castro’s PhD thesis [Reference A. Castro2] by the introduction of relative stabilizations. Castro–Islambouli–Miller–Tomova [Reference Castro, Islambouli, Miller and Tomova6] obtained a full uniqueness result by introducing relative double twists.
In this article, we introduce pseudo-trisections, an alternative framework for studying 4-manifolds with boundary. Rather than inducing open book decompositions on the boundary, they induce 3-manifold trisections in the sense of Koenig [Reference Koenig12]. Since Heegaard splittings induce 3-manifold trisections in a canonical way, pseudo-trisections can be thought of as an interpolation between Heegaard splittings of boundary 3-manifolds and classical trisections of 4-manifolds. We prove an analogous existence result to the aforementioned result of Gay–Kirby.
Theorem 1.1 Let X be a compact oriented smooth 4-manifold with non-empty connected boundary Y. Let
![]() $\tau $
be a trisection of Y. Then there is a pseudo-trisection of X which restricts to
$\tau $
be a trisection of Y. Then there is a pseudo-trisection of X which restricts to
![]() $\tau $
on the boundary.
$\tau $
on the boundary.
On the other hand, we define three types of stabilization (internal, boundary, and Heegaard) for pseudo-trisections, two of which extend notions of stabilization defined for 3-manifold trisections. We show uniqueness of pseudo-trisections up to these moves.
Theorem 1.2 Let X be a compact oriented smooth 4-manifold with non-empty connected boundary. Any two pseudo-trisections of X are equivalent up to internal, boundary, and Heegaard stabilization.
The main feature of pseudo-trisections is that they are general enough to exist with lower complexity than relative trisections. Complexity is an analog of trisection genus and is defined in Section 3. Pseudo-trisections of complexity at most 1 are classified and observed to be richer than relative trisections of equal complexity. Example 3.30 shows that
![]() $c(\natural ^\ell (S^2\times D^2)) \leq \ell $
among pseudo-trisections, whereas we expect that
$c(\natural ^\ell (S^2\times D^2)) \leq \ell $
among pseudo-trisections, whereas we expect that
![]() $c(\natural ^\ell (S^2\times D^2)) \geq 3\ell $
among relative trisections. (The latter would be true if relative trisection genus were additive under connected sum.)
$c(\natural ^\ell (S^2\times D^2)) \geq 3\ell $
among relative trisections. (The latter would be true if relative trisection genus were additive under connected sum.)
We also introduce pseudo-trisection diagrams as a method for representing pseudo-trisections, analogously to trisection diagrams [Reference Gay and Kirby7] and relative trisection diagrams [Reference Gay, Pinzón-Caicedo and Castro24]. In each of these settings, diagrams are shown to be in one-to-one correspondence with (relative) trisections when modding out by appropriate moves. We obtain an analogous result:
Theorem 1.3 The realization map
 $$ \begin{align*}\mathcal R : \{\text{pseudo-trisection diagrams}\} \to \frac{\{\text{pseudo-trisections}\}}{\text{diffeomorphism}}\end{align*} $$
$$ \begin{align*}\mathcal R : \{\text{pseudo-trisection diagrams}\} \to \frac{\{\text{pseudo-trisections}\}}{\text{diffeomorphism}}\end{align*} $$
induces a bijection
 $$ \begin{align*}\frac{\Big\{\text{pseudo-trisection diagrams}\Big\}}{\begin{matrix}\text{band and torus stabilization,}\\ \text{handleslide, isotopy}\end{matrix}} \longrightarrow \frac{\Big\{\begin{matrix}\text{compact oriented 4-manifolds}\\ \text{with one boundary component}\end{matrix}\Big\}}{\text{diffeomorphism}}.\end{align*} $$
$$ \begin{align*}\frac{\Big\{\text{pseudo-trisection diagrams}\Big\}}{\begin{matrix}\text{band and torus stabilization,}\\ \text{handleslide, isotopy}\end{matrix}} \longrightarrow \frac{\Big\{\begin{matrix}\text{compact oriented 4-manifolds}\\ \text{with one boundary component}\end{matrix}\Big\}}{\text{diffeomorphism}}.\end{align*} $$
Combined with the seeming lower complexity of pseudo-trisections, this results in a diagrammatic theory for 4-manifolds with boundary with lower complexity than relative trisection diagrams. Along the way, we introduce triple Heegaard diagrams to represent trisections of closed 3-manifolds, and the calculus thereof. This diagrammatic calculus incorporates moves inspired by Heegaard theory and plumbing of open books. A pseudo-trisection diagram of a pseudo-trisected 4-manifold has the convenient property of restricting to a triple Heegaard diagram of the induced trisection on the boundary 3-manifold. Consequently, pseudo-trisection diagrams can also be thought of as combining the theory of trisection diagrams and (roughly) Heegaard diagrams.
In the final section of the article, we extend our diagrammatic calculus from 4-manifolds with boundary to pairs
![]() $(X, \mathcal K)$
where
$(X, \mathcal K)$
where
![]() $\mathcal K$
is a surface embedded in X in pseudo-bridge position. This generalizes the theory of bridge trisections introduced by Meier–Zupan [Reference Meier and Zupan18] in the closed setting, and by Meier [Reference Meier17] in the relative setting. Pseudo-bridge trisections are defined to be compatible with pseudo-trisections, in much the same way that relative bridge trisections are compatible with relative trisections. Consequently we can define pseudo-shadow diagrams, which consist of an underlying pseudo-trisection diagram to encode the ambient 4-manifold, and additional arcs to encode the embedded surface.
$\mathcal K$
is a surface embedded in X in pseudo-bridge position. This generalizes the theory of bridge trisections introduced by Meier–Zupan [Reference Meier and Zupan18] in the closed setting, and by Meier [Reference Meier17] in the relative setting. Pseudo-bridge trisections are defined to be compatible with pseudo-trisections, in much the same way that relative bridge trisections are compatible with relative trisections. Consequently we can define pseudo-shadow diagrams, which consist of an underlying pseudo-trisection diagram to encode the ambient 4-manifold, and additional arcs to encode the embedded surface.
We finish by exploring several examples of pseudo-shadow diagrams, such as a Möbius strip in
![]() $\mathbb {CP}^2 - B^4$
, and a slice disk of a trefoil knot in
$\mathbb {CP}^2 - B^4$
, and a slice disk of a trefoil knot in
![]() $\mathbb {CP}^2 - B^4$
. Through these examples we demonstrate how to compute some invariants from pseudo-shadow diagrams, namely Euler characteristic, orientability, and homology class.
$\mathbb {CP}^2 - B^4$
. Through these examples we demonstrate how to compute some invariants from pseudo-shadow diagrams, namely Euler characteristic, orientability, and homology class.
1.1 Conventions
Hereafter Y refers to connected closed smooth 3-manifolds, and X to compact smooth oriented 4-manifolds with one boundary component. The boundary of X is denoted by Y. The indices i and j are taken to be in
![]() $\mathbb {Z}/3\mathbb {Z}$
. Bolded symbols such as
$\mathbb {Z}/3\mathbb {Z}$
. Bolded symbols such as
![]() $\boldsymbol {k}$
and
$\boldsymbol {k}$
and
![]() $\boldsymbol {y}$
represent triples of three non-negative integers
$\boldsymbol {y}$
represent triples of three non-negative integers
![]() $k_1, k_2, k_3$
, or
$k_1, k_2, k_3$
, or
![]() $y_1, y_2, y_3$
. We write
$y_1, y_2, y_3$
. We write
![]() $|\boldsymbol {k}|$
to mean the 1-norm, which in this case is just the sum of the
$|\boldsymbol {k}|$
to mean the 1-norm, which in this case is just the sum of the
![]() $k_i$
. We also write
$k_i$
. We also write
![]() $\boldsymbol \delta $
and
$\boldsymbol \delta $
and
![]() $\boldsymbol \alpha $
to represent certain collections of loops. The loops themselves are unbolded, for example
$\boldsymbol \alpha $
to represent certain collections of loops. The loops themselves are unbolded, for example
![]() $\delta _1$
or
$\delta _1$
or
![]() $\alpha $
.
$\alpha $
.
We say
![]() $N \subset M$
is neatly embedded if
$N \subset M$
is neatly embedded if
![]() $\partial N \subset \partial M$
, and N is transverse to
$\partial N \subset \partial M$
, and N is transverse to
![]() $\partial M$
. Unless otherwise stated, any arcs in surfaces with boundary or 3-manifolds with boundary are assumed to be neatly embedded. We write
$\partial M$
. Unless otherwise stated, any arcs in surfaces with boundary or 3-manifolds with boundary are assumed to be neatly embedded. We write
![]() $\mathcal K$
to denote a connected compact surface with boundary neatly embedded in X. The boundary of
$\mathcal K$
to denote a connected compact surface with boundary neatly embedded in X. The boundary of
![]() $\mathcal K$
is a link L in Y.
$\mathcal K$
is a link L in Y.
1.2 Organization of the article
In Section 2, we review 3-manifold trisections and introduce triple Heegaard diagrams. In Section 3, we introduce pseudo-trisections, three notions of stabilization, and prove Theorem 1.2. Further, pseudo-trisection are compared with relative trisections. In Section 4, we introduce pseudo-trisection diagrams, and prove Theorems 1.1 and 1.3. In Section 5, we introduce pseudo-bridge trisections and pseudo-shadow diagrams, and study several examples.
2 Trisections of 3-manifolds
In this section, we summarize some definitions concerning trisections of 3-manifolds, introduced by Dale Koenig [Reference Koenig12]. In particular, we describe stabilizations and Koenig’s result that (almost all) 3-manifold trisections are stably equivalent in this more general sense. Next, we introduce Heegaard stabilizations, inspired by stabilizations of Heegaard splittings. We show that any two trisections for any 3-manifold are equivalent up to stabilization and Heegaard stabilization. Next, we introduce triple Heegaard diagrams, an analog of Heegaard diagrams for trisections of 3-manifolds. Finally we briefly discuss complexity of 3-manifold trisections.
2.1 3-manifold trisections and stabilization
In this subsection, we review the theory of 3-manifold trisections introduced in [Reference Koenig12].
Definition 2.1 [Reference Koenig12]
A
![]() $(\boldsymbol {y}, b)$
-trisection of a 3-manifold Y is a decomposition
$(\boldsymbol {y}, b)$
-trisection of a 3-manifold Y is a decomposition
![]() $Y = Y_1 \cup Y_2 \cup Y_3$
such that
$Y = Y_1 \cup Y_2 \cup Y_3$
such that
-
• each
 $Y_i$
is a handlebody of genus
$Y_i$
is a handlebody of genus
 $y_i$
,
$y_i$
, -
• each
 $\Sigma _{i} = Y_{i-1} \cap Y_i$
is a compact connected surface with some genus
$\Sigma _{i} = Y_{i-1} \cap Y_i$
is a compact connected surface with some genus
 $p_i$
and boundary B, and
$p_i$
and boundary B, and -
•
 $B = Y_1 \cap Y_2 \cap Y_3$
is a b-component link.
$B = Y_1 \cap Y_2 \cap Y_3$
is a b-component link.
The link
![]() $B \subset Y$
is the binding of the trisection. See Figure 1 for a schematic for how the pieces fit together.
$B \subset Y$
is the binding of the trisection. See Figure 1 for a schematic for how the pieces fit together.

Figure 1: The components of a trisection of a 3-manifold Y.
Proposition 2.2 3-manifold trisections satisfy the following properties:
-
(1) Each
 $y_i$
is given by
$y_i$
is given by
 $p_i + p_{i+1} + b - 1$
. In particular,
$p_i + p_{i+1} + b - 1$
. In particular,
 $y_i$
is bounded below by
$y_i$
is bounded below by
 $b-1$
.
$b-1$
. -
(2) The genera
 $p_i$
of the surfaces
$p_i$
of the surfaces
 $\Sigma _i$
are given by
$\Sigma _i$
are given by
 $\frac {1}{2}(y_{i-1} + y_i - y_{i+1} - b + 1)$
.
$\frac {1}{2}(y_{i-1} + y_i - y_{i+1} - b + 1)$
.
Proof The first fact follows from the fact that
![]() $Y_i$
is a handlebody with boundary
$Y_i$
is a handlebody with boundary
![]() $\Sigma _i \cup \Sigma _{i+1}$
, where the surfaces are identified along their boundaries. The second fact is obtained by solving the simultaneous equations in the first fact.
$\Sigma _i \cup \Sigma _{i+1}$
, where the surfaces are identified along their boundaries. The second fact is obtained by solving the simultaneous equations in the first fact.
Example 2.3 The trivial trisection is a decomposition of
![]() $S^3$
into three 3-balls, with any two balls meeting along a common disk. The triple intersection of these balls is an unknot.
$S^3$
into three 3-balls, with any two balls meeting along a common disk. The triple intersection of these balls is an unknot.
Example 2.4 Every 3-manifold admits a trisection: one construction is to start with a Heegaard splitting
![]() $Y = H_1 \cup H_2$
. Then consider a contractible loop
$Y = H_1 \cup H_2$
. Then consider a contractible loop
![]() $\gamma $
on
$\gamma $
on
![]() $\Sigma = \partial H_1$
. This bounds a disk D in
$\Sigma = \partial H_1$
. This bounds a disk D in
![]() $\Sigma $
, and a neatly embedded parallel disk
$\Sigma $
, and a neatly embedded parallel disk
![]() $D'$
in
$D'$
in
![]() $H_1$
(by isotoping D). The surface
$H_1$
(by isotoping D). The surface
![]() $D\cup D'$
bounds a ball B in
$D\cup D'$
bounds a ball B in
![]() $H_1$
. Now
$H_1$
. Now
is a trisection of Y, with
![]() $B = \gamma $
.
$B = \gamma $
.
Another recipe to construct trisections is to start with an open book decomposition. Details for this example (and further examples) are provided in [Reference Koenig12].
Example 2.5 There is a (non-unique) connected sum of trisected 3-manifolds. Specifically one can delete a standard neighborhood of a point in the binding of two trisections. Now each 3-manifold has spherical boundary, and the spheres have induced decompositions into three wedges. An (oriented) connected sum along these spheres respecting the decomposition into wedges produces a trisection of the connected sum of the 3-manifolds.
Definition 2.6 Given a trisection
![]() $(Y_1, Y_2, Y_3)$
of a 3-manifold Y, a stabilization is a new trisection
$(Y_1, Y_2, Y_3)$
of a 3-manifold Y, a stabilization is a new trisection
![]() $(Y_1', Y_2', Y_3')$
constructed as follows:
$(Y_1', Y_2', Y_3')$
constructed as follows:
-
(1) Choose a neatly embedded non-separating arc
 $\alpha $
in
$\alpha $
in
 $\Sigma _i$
for some
$\Sigma _i$
for some
 $i \in \{1,2,3\}$
. (Such an arc exists provided
$i \in \{1,2,3\}$
. (Such an arc exists provided
 $\Sigma _i$
is not a disk.)
$\Sigma _i$
is not a disk.) -
(2) Let
 $N(\alpha )$
be a tubular neighborhood of
$N(\alpha )$
be a tubular neighborhood of
 $\alpha $
in Y, and define
$\alpha $
in Y, and define-
•
 $Y_{i+1}' = Y_{i+1} \cup \overline {N(\alpha )}$
,
$Y_{i+1}' = Y_{i+1} \cup \overline {N(\alpha )}$
, -
•
 $Y_{i}' = Y_{i} - N(\alpha )$
,
$Y_{i}' = Y_{i} - N(\alpha )$
, -
•
 $Y_{i-1}' = Y_{i-1} - N(\alpha )$
.
$Y_{i-1}' = Y_{i-1} - N(\alpha )$
.
-
See Figure 2 for a schematic of stabilization, given a non-separating arc
![]() $\alpha $
in
$\alpha $
in
![]() $\Sigma _1$
.
$\Sigma _1$
.

Figure 2: A stabilization of a trisection of a 3-manifold.
Notice that stabilization increases
![]() $y_{i+1}$
by 1 while leaving
$y_{i+1}$
by 1 while leaving
![]() $y_i$
and
$y_i$
and
![]() $y_{i-1}$
unchanged. On the other hand, b increases by 1 if both endpoints of
$y_{i-1}$
unchanged. On the other hand, b increases by 1 if both endpoints of
![]() $\alpha $
are in the same component of B, and decreases by 1 if the endpoints are in different components. See [Reference Koenig12] for examples of stabilizations.
$\alpha $
are in the same component of B, and decreases by 1 if the endpoints are in different components. See [Reference Koenig12] for examples of stabilizations.
Remark 2.7 Provided Y is not
![]() $S^3$
, any trisection of Y can be stabilized, since at least one
$S^3$
, any trisection of Y can be stabilized, since at least one
![]() $\Sigma _i$
must not be a disk. In Section 2.2, we introduce a second notion of stabilization to deal with the
$\Sigma _i$
must not be a disk. In Section 2.2, we introduce a second notion of stabilization to deal with the
![]() $S^3$
case.
$S^3$
case.
We say that two trisections
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {T}'$
of Y are isotopic if there is a diffeomorphism from Y to itself, isotopic to the identity, sending the ith sector of
$\mathcal {T}'$
of Y are isotopic if there is a diffeomorphism from Y to itself, isotopic to the identity, sending the ith sector of
![]() $\mathcal {T}$
to the ith sector of
$\mathcal {T}$
to the ith sector of
![]() $\mathcal {T}'$
. Further, we say a trisection is a stabilization of another if it can be obtained by a finite sequence of stabilizations up to isotopy. Two trisections are said to be equivalent up to stabilization or stably equivalent if there is a third trisection which is a stabilization of each of the other two.
$\mathcal {T}'$
. Further, we say a trisection is a stabilization of another if it can be obtained by a finite sequence of stabilizations up to isotopy. Two trisections are said to be equivalent up to stabilization or stably equivalent if there is a third trisection which is a stabilization of each of the other two.
Theorem 2.8 (Koenig [Reference Koenig12])
Let
![]() $\mathcal {T}, \mathcal {T}'$
be two trisections of a closed orientable 3-manifold Y. If Y is the 3-sphere, assume neither trisections are the trivial trisection. Then
$\mathcal {T}, \mathcal {T}'$
be two trisections of a closed orientable 3-manifold Y. If Y is the 3-sphere, assume neither trisections are the trivial trisection. Then
![]() $\mathcal T$
and
$\mathcal T$
and
![]() $\mathcal T'$
are equivalent up to stabilization.
$\mathcal T'$
are equivalent up to stabilization.
2.2 Heegaard stabilization
In this subsection, we introduce Heegaard stabilization.
Definition 2.9 Given a trisection
![]() $(Y_1, Y_2, Y_3)$
of a 3-manifold Y, a Heegaard stabilization is a new trisection
$(Y_1, Y_2, Y_3)$
of a 3-manifold Y, a Heegaard stabilization is a new trisection
![]() $(Y_1', Y_2', Y_3')$
constructed as follows:
$(Y_1', Y_2', Y_3')$
constructed as follows:
-
(1) Choose a neatly embedded boundary parallel arc
 $\alpha $
in
$\alpha $
in
 $Y_i$
, with both endpoints on
$Y_i$
, with both endpoints on
 $\Sigma _i$
.
$\Sigma _i$
. -
(2) Let
 $N(\alpha )$
be a tubular neighborhood of
$N(\alpha )$
be a tubular neighborhood of
 $\alpha $
in Y, and define
$\alpha $
in Y, and define-
•
 $Y_{i+1}' = Y_{i+1}$
,
$Y_{i+1}' = Y_{i+1}$
, -
•
 $Y_{i}' = Y_{i} - N(\alpha )$
,
$Y_{i}' = Y_{i} - N(\alpha )$
, -
•
 $Y_{i-1}' = Y_{i-1} \cup \overline {N(\alpha )}$
.
$Y_{i-1}' = Y_{i-1} \cup \overline {N(\alpha )}$
.
-
See Figure 3 for a schematic of Heegaard stabilization, given a non-separating arc
![]() $\alpha $
in
$\alpha $
in
![]() $Y_1$
with endpoints on
$Y_1$
with endpoints on
![]() $\Sigma _1$
. Requiring
$\Sigma _1$
. Requiring
![]() $\alpha $
to be boundary parallel ensures that each new sector is a 3-dimensional 1-handlebody.
$\alpha $
to be boundary parallel ensures that each new sector is a 3-dimensional 1-handlebody.

Figure 3: A Heegaard stabilization of a trisection of a 3-manifold.
Heegaard stabilization increases
![]() $y_i$
and
$y_i$
and
![]() $y_{i-1}$
by 1 while leaving
$y_{i-1}$
by 1 while leaving
![]() $y_{i+1}$
and b unchanged.
$y_{i+1}$
and b unchanged.
Proposition 2.10 Any two trisections of a closed orientable 3-manifold are equivalent up to stabilization and at least one Heegaard stabilization.
Proof If a trisection is trivial, Heegaard stabilizing once produces a non-trivial trisection. This means that applying at most one Heegaard stabilization, the trisections can be assumed to be non-trivial. The trisections are now equivalent up to stabilization, by Theorem 2.8.
2.3 Triple Heegaard diagrams
In this subsection, we introduce triple Heegaard diagrams, which are diagrams for 3-manifold trisections adapted from Heegaard diagrams. Given a
![]() $(\boldsymbol {y}, b)$
-trisection of a 3-manifold, a triple Heegaard diagram will consist of
$(\boldsymbol {y}, b)$
-trisection of a 3-manifold, a triple Heegaard diagram will consist of
![]() $|\boldsymbol y|$
closed curves on surfaces, with each set of
$|\boldsymbol y|$
closed curves on surfaces, with each set of
![]() $y_i$
curves determining a handlebody. This is analagous to Heegaard diagrams requiring
$y_i$
curves determining a handlebody. This is analagous to Heegaard diagrams requiring
![]() $g+g$
closed curves, with each set of g curves determining a handlebody.
$g+g$
closed curves, with each set of g curves determining a handlebody.
Definition 2.11 A cut system of curves on a closed surface
![]() $\Sigma $
of genus g is a collection of g disjoint simple closed curves that cut
$\Sigma $
of genus g is a collection of g disjoint simple closed curves that cut
![]() $\Sigma $
into a sphere with
$\Sigma $
into a sphere with
![]() $2g$
boundary components.
$2g$
boundary components.
Definition 2.12 A
![]() $(\boldsymbol {y},b)$
-triple Heegaard diagram consists of the data
$(\boldsymbol {y},b)$
-triple Heegaard diagram consists of the data
![]() $(\Sigma _1,\Sigma _2,\Sigma _3, \boldsymbol \delta _{1}, \boldsymbol \delta _2,\boldsymbol \delta _3)$
such that:
$(\Sigma _1,\Sigma _2,\Sigma _3, \boldsymbol \delta _{1}, \boldsymbol \delta _2,\boldsymbol \delta _3)$
such that:
-
(1) The
 $\Sigma _i$
are surfaces with genus
$\Sigma _i$
are surfaces with genus
 $p_i = \frac {1}{2}(y_{i-1} + y_i - y_{i+1} - b + 1)$
and b boundary components.
$p_i = \frac {1}{2}(y_{i-1} + y_i - y_{i+1} - b + 1)$
and b boundary components. -
(2) There is an identification of the boundaries of all three of the
 $\Sigma _i$
. In particular,
$\Sigma _i$
. In particular,
 $\Sigma _i \cup \Sigma _{i+1}$
is a closed surface of genus
$\Sigma _i \cup \Sigma _{i+1}$
is a closed surface of genus
 $y_i$
.
$y_i$
. -
(3) Each
 $\boldsymbol \delta _{i}$
is a collection of disjoint neatly embedded arcs and simple closed curves on
$\boldsymbol \delta _{i}$
is a collection of disjoint neatly embedded arcs and simple closed curves on
 $\Sigma _i$
and
$\Sigma _i$
and
 $\Sigma _{i+1}$
, which glues to a cut system of
$\Sigma _{i+1}$
, which glues to a cut system of
 $y_i$
curves on
$y_i$
curves on
 $\Sigma _i \cup \Sigma _{i+1}$
.
$\Sigma _i \cup \Sigma _{i+1}$
.
In other words, a triple Heegaard diagram consists of three surfaces with boundary, and curves and arcs of two colours on each surface. For notational brevity, we frequently write
![]() $(\Sigma _i, \boldsymbol \delta _i)$
instead of
$(\Sigma _i, \boldsymbol \delta _i)$
instead of
![]() $(\Sigma _1, \Sigma _2, \Sigma _3, \boldsymbol \delta _1,\boldsymbol \delta _2,\boldsymbol \delta _3)$
.
$(\Sigma _1, \Sigma _2, \Sigma _3, \boldsymbol \delta _1,\boldsymbol \delta _2,\boldsymbol \delta _3)$
.
Proposition 2.13 Triple Heegaard diagrams determine trisected 3-manifolds up to diffeomorphism. In particular, a triple Heegaard diagram whose surfaces have genera
![]() $p_1, p_2, p_3$
and b boundary components determines a
$p_1, p_2, p_3$
and b boundary components determines a
![]() $(\boldsymbol {y}, b)$
-trisection with
$(\boldsymbol {y}, b)$
-trisection with
![]() $y_i = p_i + p_{i+1} + b -1$
.
$y_i = p_i + p_{i+1} + b -1$
.
Proof For each i, the cut system on
![]() $\Sigma _i \cup \Sigma _{i+1}$
are instructions for gluing
$\Sigma _i \cup \Sigma _{i+1}$
are instructions for gluing
![]() $p_i + p_{i+1} + b - 1$
disks into
$p_i + p_{i+1} + b - 1$
disks into
![]() $\Sigma _i \cup \Sigma _{i+1}$
. A 3-ball now glues into the remaining cavity to produce a handlebody
$\Sigma _i \cup \Sigma _{i+1}$
. A 3-ball now glues into the remaining cavity to produce a handlebody
![]() $Y_i$
of genus
$Y_i$
of genus
![]() $y_i = p_i + p_{i+1} + b - 1$
. The handlebodies
$y_i = p_i + p_{i+1} + b - 1$
. The handlebodies
![]() $Y_i$
and
$Y_i$
and
![]() $Y_{i+1}$
glue along
$Y_{i+1}$
glue along
![]() $\Sigma _{i+1}$
. Gluing all three handlebodies together in this way produces a trisected closed 3-manifold. To see that the resulting trisected 3-manifold is unique up to diffeomorphism, we use that
$\Sigma _{i+1}$
. Gluing all three handlebodies together in this way produces a trisected closed 3-manifold. To see that the resulting trisected 3-manifold is unique up to diffeomorphism, we use that
![]() $\text {Diff}(B^n \text { rel } \partial )$
is contractible for
$\text {Diff}(B^n \text { rel } \partial )$
is contractible for
![]() $n=2$
and
$n=2$
and
![]() $n=3$
[Reference Hatcher9, Reference Smale23]. Suppose Y and
$n=3$
[Reference Hatcher9, Reference Smale23]. Suppose Y and
![]() $Y'$
are built from a given triple Heegaard diagram as above. We will incrementally build a diffeomorphism
$Y'$
are built from a given triple Heegaard diagram as above. We will incrementally build a diffeomorphism
![]() $Y \to Y'$
preserving the trisection structure. First, consider the identity map on
$Y \to Y'$
preserving the trisection structure. First, consider the identity map on
![]() $\cup _i \Sigma _i$
. The first steps in building Y and
$\cup _i \Sigma _i$
. The first steps in building Y and
![]() $Y'$
was to glue disks along curves in the cut system. Since
$Y'$
was to glue disks along curves in the cut system. Since
![]() $\text {Diff}(B^2 \text { rel } \partial )$
is contractible, the aforementioned map extends to
$\text {Diff}(B^2 \text { rel } \partial )$
is contractible, the aforementioned map extends to
![]() $\cup _i \Sigma _i \cup \text {\{disks\}}$
independent of how these disks are glued in. The final step is to glue in three 3-balls, and again, the map extends, since
$\cup _i \Sigma _i \cup \text {\{disks\}}$
independent of how these disks are glued in. The final step is to glue in three 3-balls, and again, the map extends, since
![]() $\text {Diff}(B^3 \text { rel } \partial )$
is contractible. This guarantees that we can build a diffeormophism
$\text {Diff}(B^3 \text { rel } \partial )$
is contractible. This guarantees that we can build a diffeormophism
![]() $Y \to Y'$
, and moreover that the diffeomorphism preserves the trisection structure. That is, Y and
$Y \to Y'$
, and moreover that the diffeomorphism preserves the trisection structure. That is, Y and
![]() $Y'$
are diffeomorphic as trisected 3-manifolds.
$Y'$
are diffeomorphic as trisected 3-manifolds.
Example 2.14 Figure 4 is an example of a triple Heegaard diagram of
![]() $T^3$
. By noting identifications of some boundary components in
$T^3$
. By noting identifications of some boundary components in
![]() $\Sigma _1$
and
$\Sigma _1$
and
![]() $\Sigma _2$
, we see that all three of
$\Sigma _2$
, we see that all three of
![]() $\Sigma _1, \Sigma _2$
and
$\Sigma _1, \Sigma _2$
and
![]() $\Sigma _3$
share the same
$\Sigma _3$
share the same
![]() $S^1$
boundary. Inspecting the pairs
$S^1$
boundary. Inspecting the pairs
![]() $(\Sigma _i \cup \Sigma _{i+1}, \boldsymbol {\delta }_i)$
, one can verify that these are cut systems on closed surfaces.
$(\Sigma _i \cup \Sigma _{i+1}, \boldsymbol {\delta }_i)$
, one can verify that these are cut systems on closed surfaces.

Figure 4: A triple Heegaard diagram of
![]() $T^3$
.
$T^3$
.
We observe that this is a diagram of
![]() $T^3$
by passing through the standard genus-3 Heegaard splitting of
$T^3$
by passing through the standard genus-3 Heegaard splitting of
![]() $T^3$
(see [Reference Biringer, Johnson and Minsky5, Example 3.5]). The standard Heegaard splitting of
$T^3$
(see [Reference Biringer, Johnson and Minsky5, Example 3.5]). The standard Heegaard splitting of
![]() $T^3$
has diagram
$T^3$
has diagram
![]() $(\Sigma _1 \cup \Sigma _2, \boldsymbol {\delta }_1, \boldsymbol {\delta }_2 \cup \boldsymbol {\delta }_3)$
. To verify that the triple Heegaard diagram of Figure 4 builds the same 3-manifold, it suffices to observe that the cut systems
$(\Sigma _1 \cup \Sigma _2, \boldsymbol {\delta }_1, \boldsymbol {\delta }_2 \cup \boldsymbol {\delta }_3)$
. To verify that the triple Heegaard diagram of Figure 4 builds the same 3-manifold, it suffices to observe that the cut systems
![]() $(\Sigma _3 \cup \Sigma _1, \boldsymbol {\delta }_3)$
and
$(\Sigma _3 \cup \Sigma _1, \boldsymbol {\delta }_3)$
and
![]() $(\Sigma _2 \cup \Sigma _3, \boldsymbol {\delta }_2)$
together determine the same handlebody as
$(\Sigma _2 \cup \Sigma _3, \boldsymbol {\delta }_2)$
together determine the same handlebody as
![]() $(\Sigma _1 \cup \Sigma _2, \boldsymbol {\delta }_2 \cup \boldsymbol {\delta }_3)$
. Indeed, the two former cut systems determine handlebodies with a common disk boundary
$(\Sigma _1 \cup \Sigma _2, \boldsymbol {\delta }_2 \cup \boldsymbol {\delta }_3)$
. Indeed, the two former cut systems determine handlebodies with a common disk boundary
![]() $\Sigma _3$
, and gluing the handlebodies along
$\Sigma _3$
, and gluing the handlebodies along
![]() $\Sigma _3$
results in the handlebody determined by the latter cut system.
$\Sigma _3$
results in the handlebody determined by the latter cut system.
Example 2.15 An open book decomposition
![]() $(\Sigma , \varphi )$
(where
$(\Sigma , \varphi )$
(where
![]() $\Sigma $
is a page of genus g and b boundary components, and
$\Sigma $
is a page of genus g and b boundary components, and
![]() $\varphi $
is the monodromy) induces a trisection of the ambient 3-manifold. The trisection is represented by a
$\varphi $
is the monodromy) induces a trisection of the ambient 3-manifold. The trisection is represented by a
![]() $(2g+b-1, 2g+b-1, 0, 1)$
-triple Heegaard diagram as follows:
$(2g+b-1, 2g+b-1, 0, 1)$
-triple Heegaard diagram as follows:
-
(1) The open book decomposition induces a genus
 $2g$
Heegaard splitting
$2g$
Heegaard splitting
 $(\Sigma \times [0,1/2]) \cup (\Sigma \times [1/2, 1])$
, where
$(\Sigma \times [0,1/2]) \cup (\Sigma \times [1/2, 1])$
, where
 $\Sigma \times \{0\}$
is identified with
$\Sigma \times \{0\}$
is identified with
 $\Sigma \times \{1\}$
by the monodromy map.
$\Sigma \times \{1\}$
by the monodromy map. -
(2) The Heegaard splitting is encoded by a Heegaard diagram
 $(\Sigma ', \boldsymbol \alpha , \boldsymbol \beta )$
which can be determined by
$(\Sigma ', \boldsymbol \alpha , \boldsymbol \beta )$
which can be determined by
 $\varphi $
. Reference [Reference Honda, Kazez and Matić10, Section 2] describes how to obtain such a diagram.
$\varphi $
. Reference [Reference Honda, Kazez and Matić10, Section 2] describes how to obtain such a diagram. -
(3) Let D be a disk in
 $\Sigma '$
disjoint from
$\Sigma '$
disjoint from
 $\boldsymbol \alpha $
and
$\boldsymbol \alpha $
and
 $\boldsymbol \beta $
. Then
$\boldsymbol \beta $
. Then
 $(\Sigma '-D, D, D, \boldsymbol \alpha , \varnothing , \boldsymbol \beta )$
is a triple Heegaard diagram of a trisection induced by the open book decomposition. (This follows the construction in Example 2.4, and is a special case of the procedure in Example 2.14.)
$(\Sigma '-D, D, D, \boldsymbol \alpha , \varnothing , \boldsymbol \beta )$
is a triple Heegaard diagram of a trisection induced by the open book decomposition. (This follows the construction in Example 2.4, and is a special case of the procedure in Example 2.14.)
A more symmetric construction is to take an open book
![]() $(\Sigma , \varphi )$
and immediately trisect the ambient manifold as
$(\Sigma , \varphi )$
and immediately trisect the ambient manifold as
![]() $(\Sigma \times [0,1/3]) \cup (\Sigma \times [1/3, 2/3]) \cup (\Sigma \times [2/3,1])$
, again identifying
$(\Sigma \times [0,1/3]) \cup (\Sigma \times [1/3, 2/3]) \cup (\Sigma \times [2/3,1])$
, again identifying
![]() $\Sigma \times \{0\}$
and
$\Sigma \times \{0\}$
and
![]() $\Sigma \times \{1\}$
by the monodromy map. However, this results in a
$\Sigma \times \{1\}$
by the monodromy map. However, this results in a
![]() $(2g+b-1, 2g+b-1, 2g+b-1,b)$
-trisection, and such a trisection can be obtained by stabilizing the
$(2g+b-1, 2g+b-1, 2g+b-1,b)$
-trisection, and such a trisection can be obtained by stabilizing the
![]() $(2g+b-1,2g+b-1,0,1)$
-trisection described above.
$(2g+b-1,2g+b-1,0,1)$
-trisection described above.
Remark 2.16 The data of a triple Heegaard diagram doesn’t explictly describe how the binding B is knotted—that is to say, the boundary
![]() $B = \partial \Sigma _i$
can be depicted in a diagram as an unlink. However, Proposition 2.13 shows that the isotopy class of the link B is nevertheless determined by triple Heegaard diagrams.
$B = \partial \Sigma _i$
can be depicted in a diagram as an unlink. However, Proposition 2.13 shows that the isotopy class of the link B is nevertheless determined by triple Heegaard diagrams.
Proposition 2.17 Every 3-manifold is described by a triple Heegaard diagram.
Proof Every 3-manifold admits a trisection, as in Example 2.4. Moreover, every trisection is induced by a triple Heegaard diagram. This is because every sector of the trisection is a handlebody, and every handlebody is determined by a cut system on the boundary surface. A collection of three cut systems for each sector is precisely the data of a triple Heegaard diagram.
Example 2.18 Figure 5 depicts stabilization along a non-separating arc in
![]() $\Sigma _1$
. Stabilizing a diagram has three steps:
$\Sigma _1$
. Stabilizing a diagram has three steps:
-
(1) Identify the non-separating arc
 $\alpha $
in some
$\alpha $
in some
 $\Sigma _i$
along which the stabilization occurs. Thicken the arc to a band in
$\Sigma _i$
along which the stabilization occurs. Thicken the arc to a band in
 $\Sigma _i$
. (The thickening is unique in the sense that the framing is determined by
$\Sigma _i$
. (The thickening is unique in the sense that the framing is determined by
 $\Sigma _i$
.)
$\Sigma _i$
.) -
(2) The new surfaces
 $\Sigma _i', \Sigma _{i+1}', \Sigma _{i+2}'$
are obtained by subtracting the band in
$\Sigma _i', \Sigma _{i+1}', \Sigma _{i+2}'$
are obtained by subtracting the band in
 $\Sigma _i'$
, and attaching the band to both
$\Sigma _i'$
, and attaching the band to both
 $\Sigma _{i+1}'$
and
$\Sigma _{i+1}'$
and
 $\Sigma _{i+2}'$
.
$\Sigma _{i+2}'$
. -
(3) The curves on
 $\Sigma _i$
intersecting
$\Sigma _i$
intersecting
 $\alpha $
are cut and pasted in the new surfaces, as shown by the change from
$\alpha $
are cut and pasted in the new surfaces, as shown by the change from
 $\delta $
to
$\delta $
to
 $\delta '$
in Figure 5. A single new curve is added to
$\delta '$
in Figure 5. A single new curve is added to
 $\boldsymbol {\delta }_{i+1}$
, consisting of an arc in each band in
$\boldsymbol {\delta }_{i+1}$
, consisting of an arc in each band in
 $\Sigma _{i+1}'$
and
$\Sigma _{i+1}'$
and
 $\Sigma _{i+2}'$
. This is
$\Sigma _{i+2}'$
. This is
 $\gamma $
in Figure 5, and corresponds to a meridian of the handle glued to
$\gamma $
in Figure 5, and corresponds to a meridian of the handle glued to
 $Y_{i+1}$
in the stabilization.
$Y_{i+1}$
in the stabilization.

Figure 5: Stabilization of triple Heegaard diagrams.
Example 2.19 Figure 6 depicts Heegaard stabilization along an arc in
![]() $Y_1$
with endpoints on
$Y_1$
with endpoints on
![]() $\Sigma _1$
. It is evidently diagrammatically similar to stabilization of Heegaard splittings. In this example, since the arc has endpoints on
$\Sigma _1$
. It is evidently diagrammatically similar to stabilization of Heegaard splittings. In this example, since the arc has endpoints on
![]() $\Sigma _1$
, the sector
$\Sigma _1$
, the sector
![]() $Y_2$
is unchanged while
$Y_2$
is unchanged while
![]() $Y_1$
and
$Y_1$
and
![]() $Y_3$
increase in genus. Therefore the two new curves
$Y_3$
increase in genus. Therefore the two new curves
![]() $\eta $
and
$\eta $
and
![]() $\gamma $
in Figure 6 belong to
$\gamma $
in Figure 6 belong to
![]() $\boldsymbol {\delta }_1$
and
$\boldsymbol {\delta }_1$
and
![]() $\boldsymbol {\delta }_3$
, respectively.
$\boldsymbol {\delta }_3$
, respectively.

Figure 6: Heegaard stabilization of triple Heegaard diagrams.
Example 2.20 Handleslides and isotopies of triple Heegaard diagrams are the same as those for Heegaard diagrams. More explicitly, given a Heegaard diagram
![]() $(\Sigma , \boldsymbol {\alpha }, \boldsymbol {\beta })$
, handleslide and isotopy moves are defined one handlebody at a time, i.e., on
$(\Sigma , \boldsymbol {\alpha }, \boldsymbol {\beta })$
, handleslide and isotopy moves are defined one handlebody at a time, i.e., on
![]() $(\Sigma , \boldsymbol {\alpha })$
and
$(\Sigma , \boldsymbol {\alpha })$
and
![]() $(\Sigma , \boldsymbol {\beta })$
. In the case of a triple Heegaard diagram
$(\Sigma , \boldsymbol {\beta })$
. In the case of a triple Heegaard diagram
![]() $(\Sigma _i, \boldsymbol {\delta }_i)$
, handleslides and isotopies are defined on the pairs
$(\Sigma _i, \boldsymbol {\delta }_i)$
, handleslides and isotopies are defined on the pairs
![]() $(\Sigma _1 \cup \Sigma _2, \boldsymbol {\delta }_2), (\Sigma _2 \cup \Sigma _3, \boldsymbol {\delta }_3)$
, and
$(\Sigma _1 \cup \Sigma _2, \boldsymbol {\delta }_2), (\Sigma _2 \cup \Sigma _3, \boldsymbol {\delta }_3)$
, and
![]() $(\Sigma _3 \cup \Sigma _1, \boldsymbol {\delta }_1)$
.
$(\Sigma _3 \cup \Sigma _1, \boldsymbol {\delta }_1)$
.
Note that isotopies and handleslides of families of curves on
![]() $\Sigma _i \cup \Sigma _{i+1}$
can change how they intersect their common boundary, as shown in Figure 7.
$\Sigma _i \cup \Sigma _{i+1}$
can change how they intersect their common boundary, as shown in Figure 7.

Figure 7: A handleslide in the context of triple Heegaard diagrams.
Lemma 2.21 Fix a trisection
![]() $(Y_1, Y_2, Y_3)$
of a 3-manifold Y. Any two triple Heegaard diagrams
$(Y_1, Y_2, Y_3)$
of a 3-manifold Y. Any two triple Heegaard diagrams
![]() $(\Sigma _i, \boldsymbol {\delta }_i), (\Sigma _i', \boldsymbol {\delta }_i')$
of
$(\Sigma _i, \boldsymbol {\delta }_i), (\Sigma _i', \boldsymbol {\delta }_i')$
of
![]() $(Y_1, Y_2, Y_3)$
are diffeomorphic after a sequence of handleslides and isotopies. (That is, there are diffeomorphisms
$(Y_1, Y_2, Y_3)$
are diffeomorphic after a sequence of handleslides and isotopies. (That is, there are diffeomorphisms
![]() $\varphi _i : \Sigma _i \to \Sigma _i'$
rel boundary sending
$\varphi _i : \Sigma _i \to \Sigma _i'$
rel boundary sending
![]() $\boldsymbol {\delta }_i \cap \Sigma _i$
and
$\boldsymbol {\delta }_i \cap \Sigma _i$
and
![]() $\boldsymbol {\delta }_{i-1} \cap \Sigma _i$
to
$\boldsymbol {\delta }_{i-1} \cap \Sigma _i$
to
![]() $\boldsymbol {\delta }_i' \cap \Sigma _i$
and
$\boldsymbol {\delta }_i' \cap \Sigma _i$
and
![]() $\boldsymbol {\delta }_{i-1}' \cap \Sigma _i$
, respectively.)
$\boldsymbol {\delta }_{i-1}' \cap \Sigma _i$
, respectively.)
Proof Johannson [Reference Johannson11] defines a meridian-system to be a pair
![]() $(M,\mathcal D)$
where M is a 3-manifold with boundary and
$(M,\mathcal D)$
where M is a 3-manifold with boundary and
![]() $\mathcal D$
is a collection of neatly embedded disks such that
$\mathcal D$
is a collection of neatly embedded disks such that
![]() $M - D$
is homeomorphic to a 3-ball. Reference [Reference Johannson11, Corollary 1.6] shows that meridian-systems of handlebodies (which are considered up to isotopy) are unique up to handleslides. Given a sector
$M - D$
is homeomorphic to a 3-ball. Reference [Reference Johannson11, Corollary 1.6] shows that meridian-systems of handlebodies (which are considered up to isotopy) are unique up to handleslides. Given a sector
![]() $Y_i$
of the trisection,
$Y_i$
of the trisection,
![]() $(\Sigma _{i}, \Sigma _{i+1}, \boldsymbol {\delta }_i)$
induces a unique meridian-system. It follows that, up to some diffeomorphism of
$(\Sigma _{i}, \Sigma _{i+1}, \boldsymbol {\delta }_i)$
induces a unique meridian-system. It follows that, up to some diffeomorphism of
![]() $(Y_1, Y_2, Y_3)$
, the triple Heegaard diagram is unique up to isotopy and handleslides. Finally, diffeomorphisms of the trisection descend to diffeomorphisms of triple Heegaard diagrams.
$(Y_1, Y_2, Y_3)$
, the triple Heegaard diagram is unique up to isotopy and handleslides. Finally, diffeomorphisms of the trisection descend to diffeomorphisms of triple Heegaard diagrams.
Proposition 2.22 Any two triple Heegaard diagrams of a given 3-manifold are diffeomorphic after a sequence of stabilizations, Heegaard stabilizations, handleslides, and isotopies.
Proof By Lemma 2.21, any two triple Heegaard diagrams of a fixed trisection are diffeomorphic after a sequence of handleslides and isotopies. By Proposition 2.10, any two trisections of a given 3-manifold are equivalent up to stabilization and Heegaard stabilization. (Examples 2.18 and 2.19 show how stabilization and Heegaard stabilization descend to triple Heegaard diagrams.) The result follows by applying each of these results.
Remark 2.23 Proposition 2.22 is a trisection version of the Reidemeister–Singer theorem [Reference Reidemeister21, Reference Singer22] for Heegaard splittings, which states that Heegaard diagrams of a given 3-manifold are diffeomorphic after a sequence of stabilizations, handleslides, and isotopies. (Strictly speaking the Reidemeister–Singer theorem refers to the result that Heegaard splittings are stably equivalent, but both original proofs were at the diagrammatic level.)
2.4 Complexity of 3-manifold trisections
This subsection introduces a notion of complexity for 3-manifold trisections, which will be used later to study the complexity of pseudo-trisections.
Definition 2.24 The complexity of a
![]() $(\boldsymbol {y}, b)$
-trisection
$(\boldsymbol {y}, b)$
-trisection
![]() $\mathcal {T}$
of a 3-manifold Y is the integer
$\mathcal {T}$
of a 3-manifold Y is the integer
![]() $c(\mathcal T) = |\boldsymbol y|$
. The minimum complexity among all trisections of Y is denoted
$c(\mathcal T) = |\boldsymbol y|$
. The minimum complexity among all trisections of Y is denoted
![]() $c(Y)$
.
$c(Y)$
.
Example 2.25 The trivial trisection of
![]() $S^3$
has complexity
$S^3$
has complexity
![]() $0$
. It follows that
$0$
. It follows that
![]() $c(S^3) = 0$
.
$c(S^3) = 0$
.
Proposition 2.26 Complexity of 3-manifold trisections satisfies the following properties:
-
(1) Recalling that
 $p_i$
denotes the genus of the surface
$p_i$
denotes the genus of the surface
 $\Sigma _i$
in the trisection
$\Sigma _i$
in the trisection
 $\mathcal T$
,
$\mathcal T$
,  $$ \begin{align*}c(\mathcal T) = 2|\boldsymbol p| + 3b - 3.\end{align*} $$
$$ \begin{align*}c(\mathcal T) = 2|\boldsymbol p| + 3b - 3.\end{align*} $$
-
(2) Stabilization increases complexity by 1, Heegaard stabilization increases complexity by 2.
-
(3) Writing
 $g_H(Y)$
to denote the minimum genus of a Heegaard splitting of Y,
$g_H(Y)$
to denote the minimum genus of a Heegaard splitting of Y,  $$ \begin{align*}c(Y) \leq 2g_H(Y).\end{align*} $$
$$ \begin{align*}c(Y) \leq 2g_H(Y).\end{align*} $$
Proof Item (1) is immediate from Proposition 2.2. Item (2) follows from earlier observations about how stabilization and Heegaard stabilization affect each
![]() $y_i$
. Finally item (3) follows from the fact that a genus g Heegaard splitting induces a
$y_i$
. Finally item (3) follows from the fact that a genus g Heegaard splitting induces a
![]() $(g, g, 0; 1)$
-trisection.
$(g, g, 0; 1)$
-trisection.
Example 2.27 (Koenig [Reference Koenig12, Example 8])
The trisection of
![]() $(S^1 \times S^2) \# (S^1 \times S^2)$
depicted in Figure 8 has complexity
$(S^1 \times S^2) \# (S^1 \times S^2)$
depicted in Figure 8 has complexity
![]() $3$
. One can show that any trisection with complexity at most
$3$
. One can show that any trisection with complexity at most
![]() $2$
is necessarily induced by a Heegaard splitting of genus at most 1, and such 3-manifolds are lens spaces or
$2$
is necessarily induced by a Heegaard splitting of genus at most 1, and such 3-manifolds are lens spaces or
![]() $(S^1 \times S^2)$
. It follows that
$(S^1 \times S^2)$
. It follows that
![]() $c((S^1 \times S^2) \# (S^1 \times S^2)) = 3$
. Moreover,
$c((S^1 \times S^2) \# (S^1 \times S^2)) = 3$
. Moreover,
![]() $g_H((S^1\times S^2) \# (S^1 \times S^2)) = 2$
, so this example shows that the inequality
$g_H((S^1\times S^2) \# (S^1 \times S^2)) = 2$
, so this example shows that the inequality
![]() $c(Y) \leq 2g_H(Y)$
can be strict.
$c(Y) \leq 2g_H(Y)$
can be strict.

Figure 8: Triple Heegaard diagram of
![]() $(S^1\times S^2) \# (S^1 \times S^2)$
with complexity 3.
$(S^1\times S^2) \# (S^1 \times S^2)$
with complexity 3.
3 Pseudo-trisections
In this section, we introduce pseudo-trisections, which are a generalization of relative trisections of compact 4-manifolds with connected boundary. We also describe several notions of stabilization, and prove that pseudo-trisections are stably equivalent. Finally we introduce complexity of pseudo-trisections and use it to compare pseudo-trisections and relative trisections.
3.1 Pseudo-trisections and their properties
In this subsection, we define pseudo-trisections and inspect some of their properties.
Definition 3.1 An n-dimensional 1-handlebody of genus k is a manifold with boundary diffeomorphic to
![]() $\natural ^k (S^1 \times B^{n-1})$
.
$\natural ^k (S^1 \times B^{n-1})$
.
Definition 3.2 A
![]() $(g, \boldsymbol {k}; \boldsymbol {y},b)$
-pseudo-trisection of a compact connected oriented smooth 4-manifold X with one boundary component
$(g, \boldsymbol {k}; \boldsymbol {y},b)$
-pseudo-trisection of a compact connected oriented smooth 4-manifold X with one boundary component
![]() $Y = \partial X$
is a decomposition
$Y = \partial X$
is a decomposition
![]() $X = X_1 \cup X_2 \cup X_3$
such that
$X = X_1 \cup X_2 \cup X_3$
such that
-
(1) each
 $X_i$
is a 4-dimensional 1-handlebody of genus
$X_i$
is a 4-dimensional 1-handlebody of genus
 $k_i$
,
$k_i$
, -
(2) each
 $H_i = X_{i-1} \cap X_i$
is a 3-dimensional 1-handlebody of genus
$H_i = X_{i-1} \cap X_i$
is a 3-dimensional 1-handlebody of genus
 $h_i$
for some
$h_i$
for some
 $h_i$
,
$h_i$
, -
(3) each
 $Y_i = X_{i} \cap \partial X$
is a 3-dimensional 1-handlebody of genus
$Y_i = X_{i} \cap \partial X$
is a 3-dimensional 1-handlebody of genus
 $y_i$
,
$y_i$
, -
(4)
 $\Sigma _C = X_1 \cap X_2 \cap X_3$
is a connected surface of genus g with b boundary components,
$\Sigma _C = X_1 \cap X_2 \cap X_3$
is a connected surface of genus g with b boundary components, -
(5) each
 $\Sigma _i = Y_{i-1} \cap Y_i$
is a connected surface of some genus
$\Sigma _i = Y_{i-1} \cap Y_i$
is a connected surface of some genus
 $p_i$
and b boundary components,
$p_i$
and b boundary components, -
(6) and
 $B = X_1 \cap X_2 \cap X_3 \cap \partial X$
is a b-component link.
$B = X_1 \cap X_2 \cap X_3 \cap \partial X$
is a b-component link.
See Figure 9 for a schematic of how the various pieces fit together.

Figure 9: The components of a pseudo-trisection of a 4-manifold X with boundary Y.
Definition 3.3 We fix some terminology: a sector of a pseudo-trisection is any of the
![]() $X_i$
. The binding of a pseudo-trisection is the link B (considered as a link in
$X_i$
. The binding of a pseudo-trisection is the link B (considered as a link in
![]() $\partial X$
). Finally, the 3-skeleton of a pseudo-trisection is the union of all 3-dimensional pieces,
$\partial X$
). Finally, the 3-skeleton of a pseudo-trisection is the union of all 3-dimensional pieces,
![]() $H_1 \cup H_2 \cup H_3 \cup \partial X$
; and the 2-skeleton of a pseudo-trisection is the union of all 2-dimensional pieces,
$H_1 \cup H_2 \cup H_3 \cup \partial X$
; and the 2-skeleton of a pseudo-trisection is the union of all 2-dimensional pieces,
![]() $\Sigma _C \cup \Sigma _1 \cup \Sigma _2 \cup \Sigma _3$
. We avoid the term spine, although it is commonly used to refer to the 3-skeleta of closed 4-manifold trisections.
$\Sigma _C \cup \Sigma _1 \cup \Sigma _2 \cup \Sigma _3$
. We avoid the term spine, although it is commonly used to refer to the 3-skeleta of closed 4-manifold trisections.
Proposition 3.4 Pseudo-trisections satisfy the following properties:
-
(1) The restriction of a
 $(g, \boldsymbol {k}, \boldsymbol {y}, b)$
-pseudo-trisection of X to
$(g, \boldsymbol {k}, \boldsymbol {y}, b)$
-pseudo-trisection of X to
 $\partial X = Y$
is a
$\partial X = Y$
is a
 $(\boldsymbol {y}, b)$
-trisection of Y.
$(\boldsymbol {y}, b)$
-trisection of Y. -
(2) The genera
 $p_i$
of the surfaces
$p_i$
of the surfaces
 $\Sigma _i$
are given by
$\Sigma _i$
are given by  $$ \begin{align*}p_i = \tfrac{1}{2}(y_{i-1} + y_i - y_{i+1} - b + 1).\end{align*} $$
$$ \begin{align*}p_i = \tfrac{1}{2}(y_{i-1} + y_i - y_{i+1} - b + 1).\end{align*} $$
-
(3) The genera
 $h_i$
of the handlebodies
$h_i$
of the handlebodies
 $H_i$
are given by
$H_i$
are given by  $$ \begin{align*}h_i = g+p_i + b - 1 = g + \tfrac{1}{2}(y_{i-1} + y_i - y_{i+1} + b - 1).\end{align*} $$
$$ \begin{align*}h_i = g+p_i + b - 1 = g + \tfrac{1}{2}(y_{i-1} + y_i - y_{i+1} + b - 1).\end{align*} $$
-
(4)
 $\chi (X) = g - |\boldsymbol {k}| + \frac {1}{2}(|\boldsymbol {y}| + b + 1)$
.
$\chi (X) = g - |\boldsymbol {k}| + \frac {1}{2}(|\boldsymbol {y}| + b + 1)$
.
Proof The first fact is immediate from the definition,specifically, items (3), (5), and (6) are exactly necessary properties for
![]() $(Y_1, Y_2, Y_3)$
to be a trisection of Y. The second fact is from Proposition 2.2, restated for completeness. The third fact follows from the fact that
$(Y_1, Y_2, Y_3)$
to be a trisection of Y. The second fact is from Proposition 2.2, restated for completeness. The third fact follows from the fact that
![]() $H_i$
has boundary
$H_i$
has boundary
![]() $\Sigma _i \cup \Sigma _C$
. Finally, the Euler characteristic formula is derived by repeated applications of the difference formula
$\Sigma _i \cup \Sigma _C$
. Finally, the Euler characteristic formula is derived by repeated applications of the difference formula
![]() $\chi (A\cup B) = \chi (A) + \chi (B) - \chi (A\cap B)$
. Note that
$\chi (A\cup B) = \chi (A) + \chi (B) - \chi (A\cap B)$
. Note that
![]() $|\boldsymbol y| + b$
is odd because
$|\boldsymbol y| + b$
is odd because
![]() $|\boldsymbol y| + b = 2|\boldsymbol p| + 4b - 3$
, so in each of the last three properties, no half-integers appear.
$|\boldsymbol y| + b = 2|\boldsymbol p| + 4b - 3$
, so in each of the last three properties, no half-integers appear.
3.2 Relative trisections
Pseudo-trisections are morally generalizations of relative trisections, described in detail in [Reference A. Castro2]. We formalize the relationship between relative trisections and pseudo-trisections in Proposition 3.18. Here we review the definition of relative trisections and some fundamental results concerning relative trisections.
In order to define relative trisections, we must first fix notation for some standard model pieces—we use notation as in [Reference Gay, Pinzón-Caicedo and Castro25]. A relative trisection will then be defined in terms of these standard pieces.
Let
![]() $g,k,p,b$
be non-negative integers with
$g,k,p,b$
be non-negative integers with
![]() $g \geq p$
and
$g \geq p$
and
![]() $g+p+b-1 \geq k \geq 2p+b-1$
. Let
$g+p+b-1 \geq k \geq 2p+b-1$
. Let
![]() $Z_k = \natural ^k S^1 \times B^3$
, and
$Z_k = \natural ^k S^1 \times B^3$
, and
![]() $Y_k = \partial Z_k = \#^k S^1 \times S^2$
. Next we describe a decomposition of
$Y_k = \partial Z_k = \#^k S^1 \times S^2$
. Next we describe a decomposition of
![]() $Y_k$
into three pieces, two corresponding to intersections of sectors in the relative trisection, and the other corresponding to a third of the boundary of the manifold.
$Y_k$
into three pieces, two corresponding to intersections of sectors in the relative trisection, and the other corresponding to a third of the boundary of the manifold.
Let
![]() $D = \{(r, \theta ): r \in [0,1], \theta \in [-\pi /3, \pi /3]\}$
. Write
$D = \{(r, \theta ): r \in [0,1], \theta \in [-\pi /3, \pi /3]\}$
. Write
where
![]() $\partial ^- D$
and
$\partial ^- D$
and
![]() $\partial ^+ D$
are the edges with
$\partial ^+ D$
are the edges with
![]() $\theta = -\pi /3$
and
$\theta = -\pi /3$
and
![]() $\theta = \pi /3$
respectively, and
$\theta = \pi /3$
respectively, and
![]() $\partial ^0 D$
is the arc. Next, let P be a surface of genus p with b boundary components, and define
$\partial ^0 D$
is the arc. Next, let P be a surface of genus p with b boundary components, and define
![]() $U = D \times P$
, with
$U = D \times P$
, with
Let
![]() $V = \natural ^{k-2p-b+1} S^1 \times B^3$
. Notice that
$V = \natural ^{k-2p-b+1} S^1 \times B^3$
. Notice that
![]() $\partial V$
has a standard Heegaard splitting. Let
$\partial V$
has a standard Heegaard splitting. Let
![]() $\partial V = \partial ^-V \cup \partial ^+V$
be the splitting obtained by stabilizing the standard Heegaard splitting exactly
$\partial V = \partial ^-V \cup \partial ^+V$
be the splitting obtained by stabilizing the standard Heegaard splitting exactly
![]() $g-k+p+b-1$
times.
$g-k+p+b-1$
times.
Since
![]() $(k-2p-b+1) + (2p+b-1) = k$
, there is an identification
$(k-2p-b+1) + (2p+b-1) = k$
, there is an identification
![]() $Z_k = U \natural V$
. In particular, the boundary connect sum can be taken so that the decompositions of the boundaries align, giving
$Z_k = U \natural V$
. In particular, the boundary connect sum can be taken so that the decompositions of the boundaries align, giving
Definition 3.5 [Reference A. Castro2]
A
![]() $(g,k;p,b)$
-trisection or
$(g,k;p,b)$
-trisection or
![]() $(g,k;p,b)$
-relative trisection of a compact connected oriented 4-manifold X with connected boundary is a decomposition
$(g,k;p,b)$
-relative trisection of a compact connected oriented 4-manifold X with connected boundary is a decomposition
![]() $X_1 \cup X_2 \cup X_3$
such that:
$X_1 \cup X_2 \cup X_3$
such that:
-
(1) there is a diffeomorphism
 $\varphi _i : X_i \to Z_k$
for each i, and
$\varphi _i : X_i \to Z_k$
for each i, and -
(2)
 $\varphi _i(X_i \cap X_{i+1}) = Y^-_{g,k;p,b}$
,
$\varphi _i(X_i \cap X_{i+1}) = Y^-_{g,k;p,b}$
,
 $\varphi _i(X_i \cap X_{i-1}) = Y^+_{g,k;,p,b}$
, and
$\varphi _i(X_i \cap X_{i-1}) = Y^+_{g,k;,p,b}$
, and
 $\varphi _i(X_i \cap \partial X) = Y^0_{g,k;p,b}$
.
$\varphi _i(X_i \cap \partial X) = Y^0_{g,k;p,b}$
.
Remark 3.6 The indices used in the theory of relative trisections are
![]() $(g,k;p,b)$
, as opposed to
$(g,k;p,b)$
, as opposed to
![]() $(g,\boldsymbol {k}; \boldsymbol {y}, b)$
for pseudo-trisections. First note that relative trisections as introduced here are balanced, so each of the
$(g,\boldsymbol {k}; \boldsymbol {y}, b)$
for pseudo-trisections. First note that relative trisections as introduced here are balanced, so each of the
![]() $k_i$
and
$k_i$
and
![]() $p_i$
are independent of i. A more significant difference is that in pseudo-trisections we’ve chosen to work with
$p_i$
are independent of i. A more significant difference is that in pseudo-trisections we’ve chosen to work with
![]() $y_i$
rather than
$y_i$
rather than
![]() $p_i$
, that is the genera of
$p_i$
, that is the genera of
![]() $Y_i$
rather than the genera of
$Y_i$
rather than the genera of
![]() $\Sigma _i$
. This is so that we can easily read off that the boundary is
$\Sigma _i$
. This is so that we can easily read off that the boundary is
![]() $(\boldsymbol {y}, b)$
-trisected. We also know how to convert between indices by Proposition 3.4.
$(\boldsymbol {y}, b)$
-trisected. We also know how to convert between indices by Proposition 3.4.
Proposition 3.7 (Gay–Kirby [Reference Gay and Kirby7])
A relative trisection of a 4-manifold restricts to an open book on the boundary.
This proposition hints at a connection between relative trisections and pseudo-trisections, as we’ve shown that trisections of 3-manifolds are generalizations of open books, and pseudo-trisections restrict to 3-manifold trisections on their boundaries.
Theorem 3.8 (Castro–Islambouli–Miller–Tomova [Reference Castro, Islambouli, Miller and Tomova6])
Any two relative trisections of a given 4-manifold X are equivalent up to interior stabilizations, relative stabilizations, and relative double twists.
Proof The reader is directed to [Reference A. Castro2] for a description of relative stabilization, and a proof that any two relative trisections of 4-manifolds are equivalent up to internal and relative stabilizations, provided the induced open books on the boundary are equivalent up to Hopf stabilization. Reference [Reference Piergallini and Zuddas20, Theorem 3.5] shows that all open books of a given 3-manifold are equivalent up to Hopf stabilization and the
![]() $\partial U$
move (described in [Reference Piergallini and Zuddas20]). The
$\partial U$
move (described in [Reference Piergallini and Zuddas20]). The
![]() $\partial U$
move is extended to the relative double twist move of relative trisections in [Reference Castro, Islambouli, Miller and Tomova6], completing the proof.
$\partial U$
move is extended to the relative double twist move of relative trisections in [Reference Castro, Islambouli, Miller and Tomova6], completing the proof.
In Section 3.5, we establish the analogous result for pseudo-trisections.
Proposition 3.9 [Reference Gay, Pinzón-Caicedo and Castro25]
Every relative trisection is uniquely encoded by a relative trisection diagram. (The diagrams are unique up to handleslides and diffeomorphism.)
We do not elaborate on the definition of a relative trisection diagram, but the key takeaway is that relative trisections are encoded by diagrams of curves on a surface. We show analogously in Section 4.1 that pseudo-trisections are uniquely encoded by pseudo-trisection diagrams.
3.3
 $\star $
-trisections
$\star $
-trisections
Another generalization of relative trisections are
![]() $\star $
-trisections, due to Aranda and Moeller [Reference Aranda and Moeller4]. We do not fully define them here, but the idea behind the definition is as follows:
$\star $
-trisections, due to Aranda and Moeller [Reference Aranda and Moeller4]. We do not fully define them here, but the idea behind the definition is as follows:
-
(1) For each
 $i \in \{1,2,3\}$
, define standard 4-dimensional sectors
$i \in \{1,2,3\}$
, define standard 4-dimensional sectors
 $Z(C^0_i, C^1_i, C^{\text {all}}_i)$
which depend on compression bodies
$Z(C^0_i, C^1_i, C^{\text {all}}_i)$
which depend on compression bodies
 $C^{*}_i$
. These are analogous to but more general than the sectors
$C^{*}_i$
. These are analogous to but more general than the sectors
 $Z_{k}$
introduced in the definition of relative trisections. In particular, they are typically not 4-dimensional 1-handlebodies.
$Z_{k}$
introduced in the definition of relative trisections. In particular, they are typically not 4-dimensional 1-handlebodies. -
(2) A compact connected oriented 4-manifold X with connected boundary is
 $\star $
-trisected if there is a decomposition
$\star $
-trisected if there is a decomposition
 $X = X_1 \cup X_2 \cup X_3$
such that each
$X = X_1 \cup X_2 \cup X_3$
such that each
 $X_i$
is diffeomorphic to
$X_i$
is diffeomorphic to
 $Z(C^0_i, C^1_i, C^{\text {all}}_i)$
, and the diffeomorphism sends pairwise intersections of the
$Z(C^0_i, C^1_i, C^{\text {all}}_i)$
, and the diffeomorphism sends pairwise intersections of the
 $X_i$
s to appropriate compression bodies
$X_i$
s to appropriate compression bodies
 $C^{*}_i$
.
$C^{*}_i$
.
The underlying motivation behind
![]() $\star $
-trisections is to generalize the intrisic topology of the sectors as much as possible, while maintaining a gluing theorem (which also holds for relative trisections).
$\star $
-trisections is to generalize the intrisic topology of the sectors as much as possible, while maintaining a gluing theorem (which also holds for relative trisections).
Theorem 3.10 (Aranda–Moeller [Reference Aranda and Moeller4])
(Informal.) Let
![]() $X, X'$
be
$X, X'$
be
![]() $\star $
-trisected 4-manifolds with boundary
$\star $
-trisected 4-manifolds with boundary
![]() $W,W'$
. Suppose there is a homeomorphism
$W,W'$
. Suppose there is a homeomorphism
![]() $f:W \to -W'$
preserving the induced circular handle decompositions. Then the
$f:W \to -W'$
preserving the induced circular handle decompositions. Then the
![]() $\star $
-trisections on X and
$\star $
-trisections on X and
![]() $X'$
glue to a trisection of the closed manifold
$X'$
glue to a trisection of the closed manifold
![]() $X\cup _f X'$
.
$X\cup _f X'$
.
Conversely, the original motivation behind pseudo-trisections was to generalize the definition of relative trisections as much as possible while maintaining the intrinsic topology of the sectors. Consequently, neither pseudo-trisections nor
![]() $\star $
-trisections can be thought of as generalizations of one-another.
$\star $
-trisections can be thought of as generalizations of one-another.
Remark 3.11 While relative trisections restrict to open books on the boundary [Reference Gay and Kirby7] and pseudo-trisections restrict to trisections on the boundary (Proposition 3.4),
![]() $\star $
-trisections restrict to circular handle decompositions (specifically with three thin levels, where thin levels are defined in [Reference Lamb and Weed13]) on the boundary [Reference Aranda and Moeller4]. Open books canonically induce both 3-manifold trisections and circular handle decompositions, but 3-manifold trisections do not generalize to circular handle decompositions or vice versa. (This is essentially because some 3-manifolds require arbitrarily many levels in circular handle decompositions, while trisections always exist.)
$\star $
-trisections restrict to circular handle decompositions (specifically with three thin levels, where thin levels are defined in [Reference Lamb and Weed13]) on the boundary [Reference Aranda and Moeller4]. Open books canonically induce both 3-manifold trisections and circular handle decompositions, but 3-manifold trisections do not generalize to circular handle decompositions or vice versa. (This is essentially because some 3-manifolds require arbitrarily many levels in circular handle decompositions, while trisections always exist.)
3.4 Examples of pseudo-trisections
In this subsection, we describe several examples of pseudo-trisections.
Example 3.12
The trivial trisection of
![]() $B^4$
. Let
$B^4$
. Let
![]() $X_1, X_2, X_3$
each be 4-balls. The boundary of each
$X_1, X_2, X_3$
each be 4-balls. The boundary of each
![]() $X_i$
further admits the trivial trisection (in the context of 3-manifolds). We denote these sectors of
$X_i$
further admits the trivial trisection (in the context of 3-manifolds). We denote these sectors of
![]() $\partial X_i$
by
$\partial X_i$
by
![]() $Y_{i,j}$
. Gluing
$Y_{i,j}$
. Gluing
![]() $X_i$
to
$X_i$
to
![]() $X_{i+1}$
by identifying
$X_{i+1}$
by identifying
![]() $Y_{i,2}$
and
$Y_{i,2}$
and
![]() $Y_{i+1,3}$
produces
$Y_{i+1,3}$
produces
![]() $B^4$
. Explicitly, the pseudo-trisection consists of:
$B^4$
. Explicitly, the pseudo-trisection consists of:
-
•
 $X_1, X_2, X_3$
as described,
$X_1, X_2, X_3$
as described, -
•
 $H_i = Y_{i-1,2} = Y_{i,3}$
,
$H_i = Y_{i-1,2} = Y_{i,3}$
, -
•
 $Y_i = Y_{i, 1}$
,
$Y_i = Y_{i, 1}$
,
and the lower dimensional pieces are obtained by appropriate intersections. Note that this is also a relative trisection.
Example 3.13
A pseudo-trisection of
![]() $B^3\times S^1$
which is not a relative trisection. Let
$B^3\times S^1$
which is not a relative trisection. Let
![]() $X_1, X_2 = B^3 \times S^1$
, and
$X_1, X_2 = B^3 \times S^1$
, and
![]() $X_3 = B^4$
.
$X_3 = B^4$
.
![]() $X_1$
and
$X_1$
and
![]() $X_2$
have boundary
$X_2$
have boundary
![]() $S^2 \times S^1$
. Consider the trisection of
$S^2 \times S^1$
. Consider the trisection of
![]() $S^2 \times S^1$
induced by its genus 1 Heegaard splitting, as well as the standard trisection of
$S^2 \times S^1$
induced by its genus 1 Heegaard splitting, as well as the standard trisection of
![]() $S^3$
. We denote these sectors by
$S^3$
. We denote these sectors by
![]() $Y_{i,j}$
, where
$Y_{i,j}$
, where
![]() $Y_{1,1}, Y_{1,2}, Y_{2,1}, Y_{2,3}$
are solid tori, and
$Y_{1,1}, Y_{1,2}, Y_{2,1}, Y_{2,3}$
are solid tori, and
![]() $Y_{1,3}$
and
$Y_{1,3}$
and
![]() $Y_{2,2}$
are solid balls. Let
$Y_{2,2}$
are solid balls. Let
![]() $Y_{3,j}$
be the sectors of the trivial trisection of the boundary of
$Y_{3,j}$
be the sectors of the trivial trisection of the boundary of
![]() $X_3$
.
$X_3$
.
We claim that gluing
![]() $X_i$
to
$X_i$
to
![]() $X_{i+1}$
by identifying
$X_{i+1}$
by identifying
![]() $Y_{i,2}$
and
$Y_{i,2}$
and
![]() $Y_{i+1, 3}$
produces
$Y_{i+1, 3}$
produces
![]() $B^3 \times S^1$
. To see this, observe that
$B^3 \times S^1$
. To see this, observe that
![]() $X_1$
and
$X_1$
and
![]() $X_2$
are glued along a copy of
$X_2$
are glued along a copy of
![]() $D^2 \times S^1$
in their boundaries. This is a boundary connected sum in the first entry, so the resulting manifold is still
$D^2 \times S^1$
in their boundaries. This is a boundary connected sum in the first entry, so the resulting manifold is still
![]() $B^3 \times S^1$
. Next,
$B^3 \times S^1$
. Next,
![]() $X_3$
is glued to
$X_3$
is glued to
![]() $X_1 \cup X_3$
along two 3-balls, but these two 3-balls also meet along a disk. The result is another boundary connected sum. It follows that the resulting manifold is
$X_1 \cup X_3$
along two 3-balls, but these two 3-balls also meet along a disk. The result is another boundary connected sum. It follows that the resulting manifold is
![]() $B^3 \times S^1$
.
$B^3 \times S^1$
.
The sectors of the pseudo-trisection are all labeled consistently with Example 3.12. See Figure 10 for a schematic of the pseudo-trisection. Note that this pseudo-trisection is not a relative trisection because the boundary doesn’t inherit an open book structure.
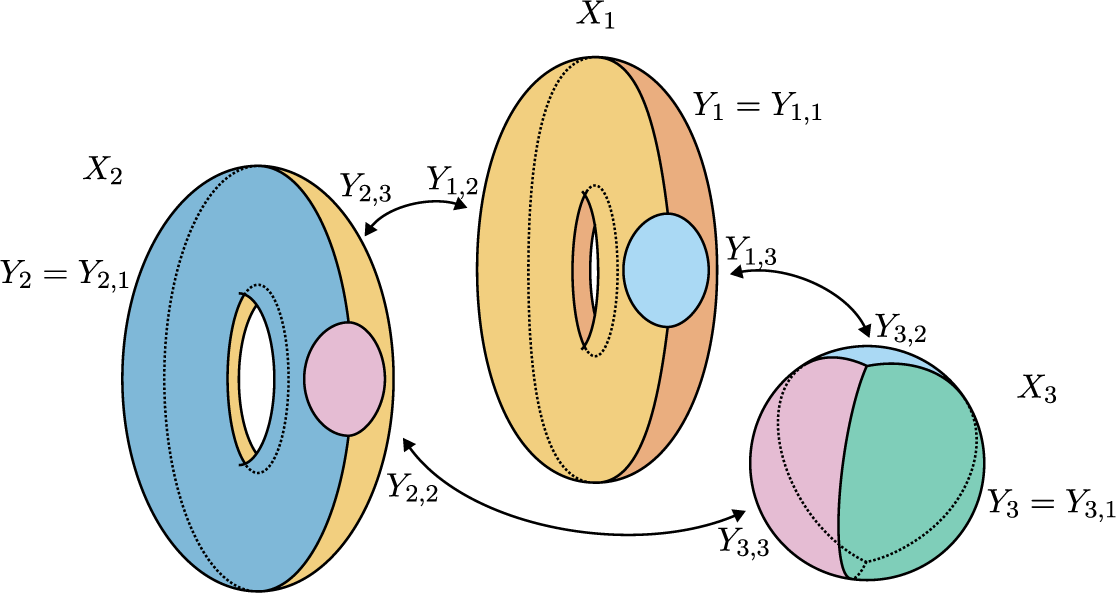
Figure 10: A schematic of how the sectors are glued together in Example 3.13.
Example 3.14
A pseudo-trisection of
![]() $B^2 \times S^2$
which is not a relative trisection. Let each of
$B^2 \times S^2$
which is not a relative trisection. Let each of
![]() $X_1,X_2,X_3$
be a 4-ball. Writing
$X_1,X_2,X_3$
be a 4-ball. Writing
![]() $X_1$
and
$X_1$
and
![]() $X_2$
as
$X_2$
as
![]() $B^2 \times B^2$
, the genus 1 Heegaard splittings of their boundaries can be written as
$B^2 \times B^2$
, the genus 1 Heegaard splittings of their boundaries can be written as
![]() $(S^1 \times B^2)\cup (B^2 \times S^1)$
. These induce trisections
$(S^1 \times B^2)\cup (B^2 \times S^1)$
. These induce trisections
In the above descriptions, B is a ball removed from a sector of the Heegaard splitting to produce a trisection, as described in Example 2.4. Let the boundary of
![]() $X_3$
be a trivially trisected
$X_3$
be a trivially trisected
![]() $S^3$
as in Example 3.13.
$S^3$
as in Example 3.13.
Gluing the three sectors as in Examples 3.12 and 3.13, we obtain a pseudo-trisection of
![]() $B^2 \times S^2$
. To see this, notice that
$B^2 \times S^2$
. To see this, notice that
![]() $X_1$
and
$X_1$
and
![]() $X_2$
are two copies of
$X_2$
are two copies of
![]() $B^2 \times B^2$
being glued along
$B^2 \times B^2$
being glued along
![]() $B^2 \times S^1$
, which produces
$B^2 \times S^1$
, which produces
![]() $B^2 \times S^2$
. As in the previous example, gluing
$B^2 \times S^2$
. As in the previous example, gluing
![]() $X_3$
does not alter the topology. Again, the sectors are labeled consistently with previous examples.
$X_3$
does not alter the topology. Again, the sectors are labeled consistently with previous examples.
Example 3.15
A pseudo-trisection of
![]() $\mathbb {CP}^2 - B^4$
. There is a standard genus 1 trisection
$\mathbb {CP}^2 - B^4$
. There is a standard genus 1 trisection
![]() $\mathcal T$
of
$\mathcal T$
of
![]() $\mathbb {CP}^2$
as seen for example in [Reference Gay and Kirby7]. A neighborhood of a point in the central surface of
$\mathbb {CP}^2$
as seen for example in [Reference Gay and Kirby7]. A neighborhood of a point in the central surface of
![]() $\mathcal T$
is a trivially trisected
$\mathcal T$
is a trivially trisected
![]() $B^4$
. Removing this ball produces a relative trisection of
$B^4$
. Removing this ball produces a relative trisection of
![]() $\mathbb {CP}^2 - B^4$
(which is also a pseudo-trisection).
$\mathbb {CP}^2 - B^4$
(which is also a pseudo-trisection).
Example 3.16 Given pseudo-trisections
![]() $(X_1,\mathcal {T}_1)$
and
$(X_1,\mathcal {T}_1)$
and
![]() $(X_2,\mathcal {T}_2)$
, there are pseudo-trisections of the form
$(X_2,\mathcal {T}_2)$
, there are pseudo-trisections of the form
![]() $\mathcal {T}_1\natural \mathcal {T}_2$
on
$\mathcal {T}_1\natural \mathcal {T}_2$
on
![]() $X_1\natural X_2$
. These are called boundary connected sums of the pseudo-trisections, and restrict to a connected sum of the boundary trisections as described in Example 2.5. These are not unique—there are generally
$X_1\natural X_2$
. These are called boundary connected sums of the pseudo-trisections, and restrict to a connected sum of the boundary trisections as described in Example 2.5. These are not unique—there are generally
![]() $3b_1 b_2$
distinct boundary connected sums, where
$3b_1 b_2$
distinct boundary connected sums, where
![]() $b_1$
and
$b_1$
and
![]() $b_2$
are the number of components of the bindings of
$b_2$
are the number of components of the bindings of
![]() $\mathcal {T}_1$
and
$\mathcal {T}_1$
and
![]() $\mathcal {T}_2$
, respectively.
$\mathcal {T}_2$
, respectively.
Explicitly, we build the boundary connected sum as follows:
-
(1) Choose points
 $q_1$
and
$q_1$
and
 $q_2$
in the bindings
$q_2$
in the bindings
 $B_1$
and
$B_1$
and
 $B_2$
of
$B_2$
of
 $\mathcal {T}_1$
and
$\mathcal {T}_1$
and
 $\mathcal {T}_2$
respectively. These each have standard neighborhoods
$\mathcal {T}_2$
respectively. These each have standard neighborhoods
 $N(q_1), N(q_2)$
in their respective pseudo-trisections, diffeomorphic to the trivial trisection. Let
$N(q_1), N(q_2)$
in their respective pseudo-trisections, diffeomorphic to the trivial trisection. Let
 $M(q_1)$
and
$M(q_1)$
and
 $M(q_2)$
denote the restriction of these neighborhoods to
$M(q_2)$
denote the restriction of these neighborhoods to
 $\partial X_1$
and
$\partial X_1$
and
 $\partial X_2$
. Note that we have made one of
$\partial X_2$
. Note that we have made one of
 $b_1 b_2$
choices in specifying
$b_1 b_2$
choices in specifying
 $q_1$
and
$q_1$
and
 $q_2$
.
$q_2$
. -
(2) The neighborhoods
 $M(q_1)$
and
$M(q_1)$
and
 $M(q_2)$
are trivially trisected in the sense that each is a 3-ball with an induced decomposition into three 3-balls, pairwise meeting along disks, with total-intersection an arc. These inherit labels
$M(q_2)$
are trivially trisected in the sense that each is a 3-ball with an induced decomposition into three 3-balls, pairwise meeting along disks, with total-intersection an arc. These inherit labels
 $(Y_1^1, Y_2^1, Y_3^1)$
and
$(Y_1^1, Y_2^1, Y_3^1)$
and
 $(Y_{1}^2, Y_2^2, Y_3^2)$
, respectively. We take the boundary connected sum of
$(Y_{1}^2, Y_2^2, Y_3^2)$
, respectively. We take the boundary connected sum of
 $X_1$
and
$X_1$
and
 $X_2$
by identifying
$X_2$
by identifying
 $M(q_1)$
with
$M(q_1)$
with
 $M(q_2)$
while further respecting the decompositions of the balls into sectors.
$M(q_2)$
while further respecting the decompositions of the balls into sectors. -
(3) There are three choices we can make, since the identification can send
 $Y_1^1$
to any one of
$Y_1^1$
to any one of
 $Y_{i}^2$
, and this determines the rest of the identification. In total, this means we have built one of
$Y_{i}^2$
, and this determines the rest of the identification. In total, this means we have built one of
 $3b_1 b_2$
possible boundary connected sums.
$3b_1 b_2$
possible boundary connected sums.
Remark 3.17 The boundary connected sum of pseudo-trisections is distinct from the plumbing of relative trisections by Murasugi sum described in [Reference Castro, Islambouli, Miller and Tomova6, Theorem 3.20]. Specifically, a boundary connected sum of two relative trisections will generally not be a relative trisection.
Proposition 3.18 A relative trisection of a 4-manifold with one boundary component is a pseudo-trisection, provided the binding of the induced open book on the boundary is non-empty.
Proof It must be shown that relative trisections as above satisfy all six of the defining properties of pseudo-trisections from Definition 3.2. Property 1 is immediate, since the definition of relative trisections requires that each sector
![]() $X_i$
is diffeomorphic to a standard piece
$X_i$
is diffeomorphic to a standard piece
![]() $Z_k$
. Properties 4, 5, and 6 are exactly observations 1, 2, and 3 at the start of [Reference Gay, Pinzón-Caicedo and Castro24, Section 4]. This leaves properties 2 and 3.
$Z_k$
. Properties 4, 5, and 6 are exactly observations 1, 2, and 3 at the start of [Reference Gay, Pinzón-Caicedo and Castro24, Section 4]. This leaves properties 2 and 3.
In a relative trisection,
![]() $H_i = X_i \cap X_{i-1}$
is necessarily diffeomorphic to a standard piece
$H_i = X_i \cap X_{i-1}$
is necessarily diffeomorphic to a standard piece
![]() $Y^+_{g,k;p,b}$
. This is a compression body from
$Y^+_{g,k;p,b}$
. This is a compression body from
![]() $\Sigma _{g,b}$
to
$\Sigma _{g,b}$
to
![]() $\Sigma _{p,b}$
obtained by compressing along
$\Sigma _{p,b}$
obtained by compressing along
![]() $g-p$
simple closed curves. In the proposition statement, we require that the binding of the induced open book in the boundary is non-empty, which is equivalent to requiring that b is at least 1. A compression body of this form is diffeomorphic to a handlebody of genus
$g-p$
simple closed curves. In the proposition statement, we require that the binding of the induced open book in the boundary is non-empty, which is equivalent to requiring that b is at least 1. A compression body of this form is diffeomorphic to a handlebody of genus
![]() $g+p+b-1$
, verifying that property 2 is satisfied.
$g+p+b-1$
, verifying that property 2 is satisfied.
Finally we must verify that property 3 is satisfied. In the notation of [Reference Gay, Pinzón-Caicedo and Castro24], we have that
![]() $X_i \cap \partial X$
is diffeomorphic to a standard piece
$X_i \cap \partial X$
is diffeomorphic to a standard piece
![]() $Y^0_{g,k;p,b}$
, which is itself equal to
$Y^0_{g,k;p,b}$
, which is itself equal to
![]() $(D \times \partial \Sigma _{p,b}) \cup (I \times \Sigma _{p,b})$
, where D is a wedge of a disk and I is the intersection of D with the boundary of the underlying disk. Topologically the union corresponds to gluing b solid tori to
$(D \times \partial \Sigma _{p,b}) \cup (I \times \Sigma _{p,b})$
, where D is a wedge of a disk and I is the intersection of D with the boundary of the underlying disk. Topologically the union corresponds to gluing b solid tori to
![]() $I \times \Sigma _{p,b}$
along their longitudes, and thus
$I \times \Sigma _{p,b}$
along their longitudes, and thus
![]() $Y^0_{g,k;p,b}$
is diffeomorphic to
$Y^0_{g,k;p,b}$
is diffeomorphic to
![]() $I \times \Sigma _{p,b}$
. Again since
$I \times \Sigma _{p,b}$
. Again since
![]() $b \geq 1$
, the latter is a handlebody (of genus
$b \geq 1$
, the latter is a handlebody (of genus
![]() $2p+b-1$
).
$2p+b-1$
).
Remark 3.19 The restriction to
![]() $(g,k,p,b)$
-relative-trisections with
$(g,k,p,b)$
-relative-trisections with
![]() $b\geq 1$
is not a strict condition. Firstly, any relative trisection can be Hopf-stabilized [Reference A. Castro2] to increase b. Secondly, the usual recipe to construct a relative trisection is to first fix an open book on the boundary 3-manifold, and this open book can be chosen to have non-empty binding.
$b\geq 1$
is not a strict condition. Firstly, any relative trisection can be Hopf-stabilized [Reference A. Castro2] to increase b. Secondly, the usual recipe to construct a relative trisection is to first fix an open book on the boundary 3-manifold, and this open book can be chosen to have non-empty binding.
Corollary 3.20 Every compact connected oriented smooth 4-manifold with connected boundary admits a pseudo-trisection.
Proof Every such 4-manifold admits a relative trisection [Reference A. Castro2]. In particular, the binding can be chosen to be non-empty. This relative trisection is a pseudo-trisection.
3.5 Stabilizations and uniqueness of pseudo-trisections
We recall internal stabilization, and introduce two more notions of stabilizations of pseudo-trisections supported near the boundary. We then show that any pseudo-trisections of a given compact 4-manifold with connected boundary are equivalent under these three notions of stabilization.
In [Reference A. Castro2], it is shown that relative trisections of a given 4-manifold with boundary X are stably equivalent, provided their boundaries are stably equivalent. More precisely, two notions of stabilization are used: internal stabilization, which doesn’t affect the open book on the boundary, and Hopf stabilization which stabilizes the open book in the boundary by adding a Hopf band. However, not all open books of a given 3-manifold are equivalent under Hopf stabilization.
In the context of pseudo-trisections, the boundary 3-manifold is equipped with a trisection rather than an open book, and all trisections of a given 3-manifold are related by appropriate notions of stabilization. This allows us to define a set of moves so that for any given 4-manifold, all pseudo-trisections of the manifold are stably equivalent, without conditioning over the boundary.
Definition 3.21 Given a pseudo-trisection
![]() $(X_1, X_2, X_3)$
of a 4-manifold X, an internal stabilization is a new pseudo-trisection
$(X_1, X_2, X_3)$
of a 4-manifold X, an internal stabilization is a new pseudo-trisection
![]() $(X_1', X_2', X_3')$
of X constructed as follows:
$(X_1', X_2', X_3')$
of X constructed as follows:
-
(1) Choose a neatly embedded boundary parallel arc
 $\alpha $
in
$\alpha $
in
 $H_i = X_i \cap X_{i-1}$
for some i, with endpoints on
$H_i = X_i \cap X_{i-1}$
for some i, with endpoints on
 $\Sigma _C = X_1 \cap X_2 \cap X_3$
.
$\Sigma _C = X_1 \cap X_2 \cap X_3$
. -
(2) Let
 $N(\alpha )$
be a tubular neighborhood of
$N(\alpha )$
be a tubular neighborhood of
 $\alpha $
in X supported away from
$\alpha $
in X supported away from
 $\partial X$
, and define
$\partial X$
, and define-
•
 $X_{i+1}' = X_{i+1} \cup \overline {N(\alpha )}$
,
$X_{i+1}' = X_{i+1} \cup \overline {N(\alpha )}$
, -
•
 $X_{i}' = X_i - N(\alpha )$
,
$X_{i}' = X_i - N(\alpha )$
, -
•
 $X_{i-1}' = X_{i-1} - N(\alpha )$
.
$X_{i-1}' = X_{i-1} - N(\alpha )$
.
-
See Figure 11 (left) for a schematic of internal stabilization.

Figure 11: From left to right: schematics of internal stabilization, boundary stabilization, and Heegaard stabilization.
Notice that stabilization increases the handlebody genus
![]() $k_{i+1}$
of
$k_{i+1}$
of
![]() $X_{i+1}$
by 1, while leaving
$X_{i+1}$
by 1, while leaving
![]() $k_i$
and
$k_i$
and
![]() $k_{i-1}$
unchanged. The genus g of
$k_{i-1}$
unchanged. The genus g of
![]() $\Sigma _C$
also increases by 1. This move is essentially “one third” of the usual notion of stabilization for balanced trisections of closed 4-manifolds.
$\Sigma _C$
also increases by 1. This move is essentially “one third” of the usual notion of stabilization for balanced trisections of closed 4-manifolds.
Definition 3.22 Given a pseudo-trisection
![]() $(X_1, X_2, X_3)$
of a 4-manifold X with boundary Y, a boundary stabilization is a new pseudo-trisection
$(X_1, X_2, X_3)$
of a 4-manifold X with boundary Y, a boundary stabilization is a new pseudo-trisection
![]() $(X_1', X_2', X_3')$
of X constructed as follows:
$(X_1', X_2', X_3')$
of X constructed as follows:
-
(1) Choose a neatly embedded non-separating arc
 $\alpha $
in
$\alpha $
in
 $\Sigma _i$
. (Such an arc exists provided
$\Sigma _i$
. (Such an arc exists provided
 $\Sigma _i$
is not a disk.)
$\Sigma _i$
is not a disk.) -
(2) Let
 $N(\alpha )$
be a tubular neighborhood of
$N(\alpha )$
be a tubular neighborhood of
 $\alpha $
in X, and define
$\alpha $
in X, and define-
•
 $X_{i+1}' = X_{i+1} \cup \overline {N(\alpha )}$
,
$X_{i+1}' = X_{i+1} \cup \overline {N(\alpha )}$
, -
•
 $X_{i}' = X_i - N(\alpha )$
,
$X_{i}' = X_i - N(\alpha )$
, -
•
 $X_{i-1}' = X_{i-1} - N(\alpha )$
.
$X_{i-1}' = X_{i-1} - N(\alpha )$
.
-
See Figure 11 (middle) for a schematic of boundary stabilization.
The definition looks very similar to that of internal stabilization—one way to differentiate them is that internal stabilization is defined with an arc
![]() $\alpha $
in
$\alpha $
in
![]() $H_i$
that is far from
$H_i$
that is far from
![]() $\Sigma _i = H_i \cap \partial X$
, while boundary stabilization is defined with an arc
$\Sigma _i = H_i \cap \partial X$
, while boundary stabilization is defined with an arc
![]() $\alpha $
that lives entirely in
$\alpha $
that lives entirely in
![]() $\partial X$
.
$\partial X$
.
We make the following observations:
-
(1) The restriction of
 $N(\alpha )$
to Y is a tubular neighborhood of
$N(\alpha )$
to Y is a tubular neighborhood of
 $\alpha $
in Y. Therefore the restriction of
$\alpha $
in Y. Therefore the restriction of
 $(X_1', X_2', X_3')$
to Y is a stabilization (in the sense of Definition 2.6) of the restriction of
$(X_1', X_2', X_3')$
to Y is a stabilization (in the sense of Definition 2.6) of the restriction of
 $(X_1, X_2, X_3)$
to Y. (More succinctly, the restriction of a boundary stabilization is a 3-manifold stabilization of the restriction.) In particular, if
$(X_1, X_2, X_3)$
to Y. (More succinctly, the restriction of a boundary stabilization is a 3-manifold stabilization of the restriction.) In particular, if
 $(X_1, X_2, X_3)$
was a
$(X_1, X_2, X_3)$
was a
 $(g, \boldsymbol k; \boldsymbol y, b)$
-pseudo-trisection of X, then in the stabilization
$(g, \boldsymbol k; \boldsymbol y, b)$
-pseudo-trisection of X, then in the stabilization
 $\boldsymbol y$
and b change as described in Section 2.1.
$\boldsymbol y$
and b change as described in Section 2.1. -
(2) The genera
 $\boldsymbol k$
of the 4-dimensional sectors change in the same way as
$\boldsymbol k$
of the 4-dimensional sectors change in the same way as
 $\boldsymbol y$
. That is,
$\boldsymbol y$
. That is,
 $k_{i+1}$
increases by 1, while
$k_{i+1}$
increases by 1, while
 $k_i$
and
$k_i$
and
 $k_{i-1}$
are unchanged.
$k_{i-1}$
are unchanged. -
(3) The genus g of
 $\Sigma _C$
increases by 1 if the endpoints of
$\Sigma _C$
increases by 1 if the endpoints of
 $\alpha $
lie in different components of B, and is unchanged if the endpoints of
$\alpha $
lie in different components of B, and is unchanged if the endpoints of
 $\alpha $
lie in the same component. This can be seen directly, as boundary stabilization descends to a band attachment on
$\alpha $
lie in the same component. This can be seen directly, as boundary stabilization descends to a band attachment on
 $\Sigma _C$
, but it can also be deduced using the Euler characteristic formula for pseudo-trisections in Proposition 3.4.
$\Sigma _C$
, but it can also be deduced using the Euler characteristic formula for pseudo-trisections in Proposition 3.4.
Definition 3.23 Given a pseudo-trisection
![]() $(X_1, X_2, X_3)$
of a 4-manifold X with boundary Y, a Heegaard stabilization is a new pseudo-trisection
$(X_1, X_2, X_3)$
of a 4-manifold X with boundary Y, a Heegaard stabilization is a new pseudo-trisection
![]() $(X_1', X_2', X_3')$
of X constructed as follows:
$(X_1', X_2', X_3')$
of X constructed as follows:
-
(1) Choose a neatly embedded boundary parallel arc
 $\alpha $
in
$\alpha $
in
 $Y_i = X_i \cap \partial X$
for some i, with both endpoints on
$Y_i = X_i \cap \partial X$
for some i, with both endpoints on
 $\Sigma _i$
.
$\Sigma _i$
. -
(2) Let
 $N(\alpha )$
be a tubular neighborhood of
$N(\alpha )$
be a tubular neighborhood of
 $\alpha $
in
$\alpha $
in
 $X_i$
, and define
$X_i$
, and define-
•
 $X_{i+1}' = X_{i+1}$
,
$X_{i+1}' = X_{i+1}$
, -
•
 $X_i' = X_i - N(\alpha )$
,
$X_i' = X_i - N(\alpha )$
, -
•
 $X_{i-1}' = X_{i-1} \cup \overline {N(\alpha )}$
.
$X_{i-1}' = X_{i-1} \cup \overline {N(\alpha )}$
.
-
See Figure 11 (right) for a schematic of Heegaard stabilization.
We make the following observations:
-
(1) Analogously to boundary stabilizations restricting to stabiliations of the boundary, a Heegaard stabilization of a pseudo-trisection restricts to a Heegaard stabilization of the 3-manifold trisection of the boundary Y. In particular, a Heegaard stabilization of a pseudo-trisection changes
 $y_i$
and
$y_i$
and
 $y_i-1$
by 1, while leaving
$y_i-1$
by 1, while leaving
 $y_{i+1}$
and b unchanged.
$y_{i+1}$
and b unchanged. -
(2) The sector
 $X_{i-1}$
gains a 1-handle in the stabilization, so
$X_{i-1}$
gains a 1-handle in the stabilization, so
 $k_{i-1}$
increases by 1. On the other hand,
$k_{i-1}$
increases by 1. On the other hand,
 $N(\alpha )$
being carved out of
$N(\alpha )$
being carved out of
 $X_{i}$
does not change the topology of
$X_{i}$
does not change the topology of
 $X_{i}$
, since
$X_{i}$
, since
 $N(\alpha )$
runs along the boundary of
$N(\alpha )$
runs along the boundary of
 $X_{i}$
. Therefore
$X_{i}$
. Therefore
 $k_{i}$
and
$k_{i}$
and
 $k_{i+1}$
are unchanged.
$k_{i+1}$
are unchanged. -
(3) The central surface
 $\Sigma _C$
is unchanged, so b is unchanged. One can verify that all of these index changes are compatible with the Euler characteristic formula.
$\Sigma _C$
is unchanged, so b is unchanged. One can verify that all of these index changes are compatible with the Euler characteristic formula.
Internal stabilization and Heegaard stabilization are unified into the single notion of torus stabilization at the diagrammatic level, introduced later in Definition 4.7.
Theorem 1.2 Let X be a compact connected oriented smooth 4-manifold with one boundary component. Any two pseudo-trisections of X are equivalent up to internal, boundary, and Heegaard stabilization.
Proof There are two steps: first we stabilize the pseudo trisections to agree on the boundary, and then stabilize the interior.
Let
![]() $\mathcal T, \mathcal T'$
be pseudo-trisections of X. Their restrictions
$\mathcal T, \mathcal T'$
be pseudo-trisections of X. Their restrictions
![]() $\tau , \tau '$
to
$\tau , \tau '$
to
![]() $Y = \partial X$
are trisections of Y. By Proposition 2.10,
$Y = \partial X$
are trisections of Y. By Proposition 2.10,
![]() $\tau $
and
$\tau $
and
![]() $\tau '$
are stably equivalent. This means there is a trisection
$\tau '$
are stably equivalent. This means there is a trisection
![]() $\sigma $
of Y and arcs
$\sigma $
of Y and arcs
![]() $\{\alpha \}, \{\alpha '\}$
such that stabilizations and Heegaard stabilizations of
$\{\alpha \}, \{\alpha '\}$
such that stabilizations and Heegaard stabilizations of
![]() $\tau $
along
$\tau $
along
![]() $\{\alpha \}$
produces
$\{\alpha \}$
produces
![]() $\sigma $
, and similarly stabilizations and Heegaard stabilizations of
$\sigma $
, and similarly stabilizations and Heegaard stabilizations of
![]() $\tau '$
along
$\tau '$
along
![]() $\{\alpha '\}$
produces
$\{\alpha '\}$
produces
![]() $\sigma $
.
$\sigma $
.
We now return to 4-dimensions: Boundary stabilizing and Heegaard stabilizing
![]() $\mathcal T$
along
$\mathcal T$
along
![]() $\{\alpha \}$
produces a pseudo-trisection
$\{\alpha \}$
produces a pseudo-trisection
![]() $\mathcal S$
which restricts to the 3-manifold trisection
$\mathcal S$
which restricts to the 3-manifold trisection
![]() $\sigma $
on Y. On the other hand, boundary and Heegaard stabilizing
$\sigma $
on Y. On the other hand, boundary and Heegaard stabilizing
![]() $\mathcal T'$
along
$\mathcal T'$
along
![]() $\{\alpha '\}$
produces a pseudo-trisection
$\{\alpha '\}$
produces a pseudo-trisection
![]() $\mathcal S'$
which also restricts to
$\mathcal S'$
which also restricts to
![]() $\sigma $
on Y. We have successfully stabilized our pseudo-trisections to agree on the boundary.
$\sigma $
on Y. We have successfully stabilized our pseudo-trisections to agree on the boundary.
Next we turn to the interior. We proceed as in the proof of the analogous result for closed trisections in [Reference Gay and Kirby7]. To that end, we require a cobordism structure on X, which we obtain by first turning our boundary trisection into a Heegaard splitting.
Consider the sectors
![]() $X_1$
and
$X_1$
and
![]() $X_1'$
in
$X_1'$
in
![]() $\mathcal S$
and
$\mathcal S$
and
![]() $\mathcal S'$
respectively. These restrict to
$\mathcal S'$
respectively. These restrict to
![]() $Y_1 = Y_1'$
on the boundary. Choose a maximal collection of non-separating arcs in
$Y_1 = Y_1'$
on the boundary. Choose a maximal collection of non-separating arcs in
![]() $\Sigma _3$
. Boundary stabilizing the two pseudo-trisections along these arcs produces two new pseudo-trisections (which we still call
$\Sigma _3$
. Boundary stabilizing the two pseudo-trisections along these arcs produces two new pseudo-trisections (which we still call
![]() $\mathcal S$
and
$\mathcal S$
and
![]() $\mathcal S'$
). However, the restricted trisection on the boundary now has that
$\mathcal S'$
). However, the restricted trisection on the boundary now has that
![]() $\Sigma _3$
is a disk. This means
$\Sigma _3$
is a disk. This means
![]() $Y_{2}\cup Y_{3}$
now glues along a disk, so it is itself a handlebody. In summary, the decomposition
$Y_{2}\cup Y_{3}$
now glues along a disk, so it is itself a handlebody. In summary, the decomposition
![]() $Y_{1} \cup (Y_{2} \cup Y_{3})$
is a Heegaard splitting.
$Y_{1} \cup (Y_{2} \cup Y_{3})$
is a Heegaard splitting.
Next we view X as a cobordism from
![]() $Y_{2} \cup Y_{3}$
to
$Y_{2} \cup Y_{3}$
to
![]() $Y_{1}$
. Formally, we do this by considering a tubular neighborhood N of the Heegaard splitting surface
$Y_{1}$
. Formally, we do this by considering a tubular neighborhood N of the Heegaard splitting surface
![]() $\Sigma _{1}\cup \Sigma _{2}$
, so that Y is of the form
$\Sigma _{1}\cup \Sigma _{2}$
, so that Y is of the form
![]() $(Y_1-N) \cup N \cup (Y_2 \cup Y_3 - N)$
. The theorem now essentially follows from [Reference Gay and Kirby7, Theorem 21]: there are relative handle decompositions (equivalently, Morse functions), induced by the pseudo-trisections and compatible with the cobordism structure. Cerf theory tells us that the handle decompositions are related by a series of moves which correspond to internal stabilization. In summary, after a sequence of internal stabilizations, our pseudo-trisections are isotopic.
$(Y_1-N) \cup N \cup (Y_2 \cup Y_3 - N)$
. The theorem now essentially follows from [Reference Gay and Kirby7, Theorem 21]: there are relative handle decompositions (equivalently, Morse functions), induced by the pseudo-trisections and compatible with the cobordism structure. Cerf theory tells us that the handle decompositions are related by a series of moves which correspond to internal stabilization. In summary, after a sequence of internal stabilizations, our pseudo-trisections are isotopic.
Remark 3.24 The proof of Theorem 1.2 doesn’t involve Heegaard stabilization unless one of the original trisections of X restricts to the trivial open book on Y. For example, if the boundary of X is not a sphere, the above theorem holds using only boundary and internal stabilizations.
3.6 Complexity of pseudo-trisections and relative trisections
This subsection introduces a notion of complexity for pseudo-trisections, which also applies to relative trisections. It can be considered a generalization of the genus of a trisection (of a closed manifold). We show that each notion of stabilization increases complexity by 1. The minimal complexity of a pseudo-trisection of a given 4-manifold with boundary is bounded above by the minimal complexity of a relative trisection (since relative trisections are pseudo-trisections), but we see with some examples that these minimal complexities do not generally agree.
Definition 3.25 The complexity of a
![]() $(g,\boldsymbol {k},\boldsymbol {y},b)$
-pseudo-trisection
$(g,\boldsymbol {k},\boldsymbol {y},b)$
-pseudo-trisection
![]() $\mathcal {T}$
of a 4-manifold X with boundary
$\mathcal {T}$
of a 4-manifold X with boundary
![]() $\partial X$
is the integer
$\partial X$
is the integer
Further, we write
![]() $c(\partial \mathcal T)$
to denote the complexity of the induced trisection on
$c(\partial \mathcal T)$
to denote the complexity of the induced trisection on
![]() $\partial X$
, and
$\partial X$
, and
![]() $c(\mathcal T, \partial \mathcal T)$
to denote
$c(\mathcal T, \partial \mathcal T)$
to denote
![]() $c(\mathcal T) + c(\partial \mathcal T)$
. We write
$c(\mathcal T) + c(\partial \mathcal T)$
. We write
![]() $c(X)$
to denote the minimum complexity among all pseudo-trisections of X, and
$c(X)$
to denote the minimum complexity among all pseudo-trisections of X, and
![]() $c(X,\partial X)$
to denote the minimum value of
$c(X,\partial X)$
to denote the minimum value of
![]() $c(\mathcal T, \partial \mathcal T)$
among all pseudo-trisections of X.
$c(\mathcal T, \partial \mathcal T)$
among all pseudo-trisections of X.
Remark 3.26 It is immediate that
![]() $c(X,\partial X)$
is at least
$c(X,\partial X)$
is at least
![]() $c(X) + c(\partial X)$
, but it is not known whether or not they are always equal.
$c(X) + c(\partial X)$
, but it is not known whether or not they are always equal.
Proposition 3.27 Complexity satisfies the following properties:
-
(1) Recalling that
 $p_i$
denotes the genus of the surface
$p_i$
denotes the genus of the surface
 $\Sigma _i$
of the pseudo-trisection,
$\Sigma _i$
of the pseudo-trisection,  $$ \begin{align*}c(\mathcal{T}) = g + \frac{1}{2}(|\boldsymbol{y}| + b - 1) = g + |\boldsymbol{p}| + 2b - 2.\end{align*} $$
$$ \begin{align*}c(\mathcal{T}) = g + \frac{1}{2}(|\boldsymbol{y}| + b - 1) = g + |\boldsymbol{p}| + 2b - 2.\end{align*} $$
-
(2) The three types of stabilization for pseudo-trisections increase complexity by 1.
-
(3) Write
 $\beta _i$
for the Betti numbers of X.
$\beta _i$
for the Betti numbers of X.-
(a) For
 $\mathcal {T}$
a relative trisection,
$\mathcal {T}$
a relative trisection,
 $c(\mathcal {T}) \geq \beta _1 + \beta _2$
.
$c(\mathcal {T}) \geq \beta _1 + \beta _2$
. -
(b) For
 $\mathcal {T}$
a pseudo-trisection,
$\mathcal {T}$
a pseudo-trisection,
 $c(\mathcal {T},\partial \mathcal {T})\geq \beta _1 + \beta _2$
.
$c(\mathcal {T},\partial \mathcal {T})\geq \beta _1 + \beta _2$
.
-
-
(4) Given pseudo-trisected manifolds
 $(X_1, \mathcal {T}_1)$
,
$(X_1, \mathcal {T}_1)$
,
 $(X_2,\mathcal {T}_2)$
, complexity is additive in the sense that
$(X_2,\mathcal {T}_2)$
, complexity is additive in the sense that
 $c(\mathcal {T}_1 \natural \mathcal {T}_2) = c(\mathcal {T}_1) + c(\mathcal {T}_2)$
.
$c(\mathcal {T}_1 \natural \mathcal {T}_2) = c(\mathcal {T}_1) + c(\mathcal {T}_2)$
.
Proof In item (1), the first equality is an application of the last item in Proposition 3.4. The second equality is an application of the second item in the aforementioned proposition.
For item (2), we use the observation that each of the three types of stabilization for pseudo-trisections increases one of the
![]() $k_i$
by 1, while leaving the other two unchanged.
$k_i$
by 1, while leaving the other two unchanged.
For item (3), we require several steps. In step 1, we establish a general homological statement about 4-manifolds with boundary. In step 2 we establish bounds for
![]() $\beta _1$
in terms of
$\beta _1$
in terms of
![]() $|\boldsymbol {k}|$
(and
$|\boldsymbol {k}|$
(and
![]() $|\boldsymbol {y}|$
) for relative trisections (and pseudo-trisections).
$|\boldsymbol {y}|$
) for relative trisections (and pseudo-trisections).
Step 1. In the long exact sequence
![]() $H_4(X,\partial X) \xrightarrow {i} H_3(\partial X) \xrightarrow {j} H_3(X) \xrightarrow {k} H_3(X,\partial X)$
, the map k is necessarily injective because i is an isomorphism. Combining this fact with the isomorphism
$H_4(X,\partial X) \xrightarrow {i} H_3(\partial X) \xrightarrow {j} H_3(X) \xrightarrow {k} H_3(X,\partial X)$
, the map k is necessarily injective because i is an isomorphism. Combining this fact with the isomorphism
![]() $H^1(X) \cong H_3(X,\partial X)$
, we have
$H^1(X) \cong H_3(X,\partial X)$
, we have
On the other hand,
![]() $\chi (X) = 1 - \beta _1 + \beta _2 - \beta _3$
, so
$\chi (X) = 1 - \beta _1 + \beta _2 - \beta _3$
, so
Step 2. Suppose
![]() $\mathcal {T}$
is either a relative trisection or pseudo-trisection. Let
$\mathcal {T}$
is either a relative trisection or pseudo-trisection. Let
![]() $\gamma $
be a neatly embedded loop in X. Then
$\gamma $
be a neatly embedded loop in X. Then
![]() $\gamma $
meets each
$\gamma $
meets each
![]() $X_i$
along a set of arcs whose endpoints lie in
$X_i$
along a set of arcs whose endpoints lie in
![]() $\partial X_i$
. Since each
$\partial X_i$
. Since each
![]() $X_i$
is a handlebody, the arcs can be homotoped rel boundary to lie in
$X_i$
is a handlebody, the arcs can be homotoped rel boundary to lie in
![]() $\partial X_i$
. We do this in every sector, to obtain a loop
$\partial X_i$
. We do this in every sector, to obtain a loop
![]() $\gamma '$
contained entirely within the 3-skeleton of
$\gamma '$
contained entirely within the 3-skeleton of
![]() $\mathcal {T}$
. Next we repeat this step a dimension lower:
$\mathcal {T}$
. Next we repeat this step a dimension lower:
![]() $\gamma '$
intersects each
$\gamma '$
intersects each
![]() $H_i$
or
$H_i$
or
![]() $Y_i$
along an arc with endpoints in
$Y_i$
along an arc with endpoints in
![]() $\partial H_i$
or
$\partial H_i$
or
![]() $\partial Y_i$
respectively. These arcs can again be homotoped rel boundary to lie within
$\partial Y_i$
respectively. These arcs can again be homotoped rel boundary to lie within
![]() $\partial H_i$
and
$\partial H_i$
and
![]() $\partial Y_i$
respectively. Doing this in every 3-dimensional sector, we obtain a loop
$\partial Y_i$
respectively. Doing this in every 3-dimensional sector, we obtain a loop
![]() $\gamma "$
contained entirely within the 2-skeleton of
$\gamma "$
contained entirely within the 2-skeleton of
![]() $\mathcal {T}$
.
$\mathcal {T}$
.
The proof now diverges for pseudo-trisections and relative trisections. In the former case, notice that
![]() $\gamma "$
can be viewed as loop in
$\gamma "$
can be viewed as loop in
![]() $X_i \cup \Sigma _{i-1}$
for any i. This means
$X_i \cup \Sigma _{i-1}$
for any i. This means
![]() $\pi _1(X_i \cup \Sigma _{i-1})$
surjects onto
$\pi _1(X_i \cup \Sigma _{i-1})$
surjects onto
![]() $\pi _1(X)$
. Taking into account how
$\pi _1(X)$
. Taking into account how
![]() $\Sigma _{i-1}$
is glued to
$\Sigma _{i-1}$
is glued to
![]() $X_i$
, it follows that
$X_i$
, it follows that
![]() $2p_{i-1} + b - 1 + k_i \geq \beta _1$
. This holds over each i, giving
$2p_{i-1} + b - 1 + k_i \geq \beta _1$
. This holds over each i, giving
Combining this with the result from step 1 gives
In the case of relative trisections, the boundary is an open book. Therefore the arcs
![]() $\gamma " \cap \Sigma _i$
can be homotoped rel boundary to any
$\gamma " \cap \Sigma _i$
can be homotoped rel boundary to any
![]() $\Sigma _j$
via the fibration defining the open book. It follows that
$\Sigma _j$
via the fibration defining the open book. It follows that
![]() $\gamma "$
can be homotoped to lie entirely within any one of the
$\gamma "$
can be homotoped to lie entirely within any one of the
![]() $X_i$
. It follows that
$X_i$
. It follows that
![]() $|\boldsymbol {k}| \geq 3\beta _1$
, and therefore that
$|\boldsymbol {k}| \geq 3\beta _1$
, and therefore that
![]() $c(\mathcal {T}) \geq \beta _1 + \beta _2$
.
$c(\mathcal {T}) \geq \beta _1 + \beta _2$
.
Finally, for item (4), we have that
 $$ \begin{align*} c(\mathcal{T}_1\natural \mathcal{T}_2) &= \chi(X_1\natural X_2) + |\boldsymbol{k}_{\mathcal{T}_1 + \mathcal{T}_2}| - 1\\ &= \chi(X_1) + \chi(X_2) - 1 + |\boldsymbol{k}_{\mathcal{T}_1}|+|\boldsymbol{k}_{\mathcal{T}_2}| - 1 = c(\mathcal{T}_1) + c(\mathcal{T}_2) \end{align*} $$
$$ \begin{align*} c(\mathcal{T}_1\natural \mathcal{T}_2) &= \chi(X_1\natural X_2) + |\boldsymbol{k}_{\mathcal{T}_1 + \mathcal{T}_2}| - 1\\ &= \chi(X_1) + \chi(X_2) - 1 + |\boldsymbol{k}_{\mathcal{T}_1}|+|\boldsymbol{k}_{\mathcal{T}_2}| - 1 = c(\mathcal{T}_1) + c(\mathcal{T}_2) \end{align*} $$
as required.
Remark 3.28 Proposition 3.27 implies that
![]() $c(X_1\natural X_2) \leq c(X_1) + c(X_2)$
. It is not known if this inequality is ever strict. This is analogous to the question of whether or not trisection genus is additive under connected sum.
$c(X_1\natural X_2) \leq c(X_1) + c(X_2)$
. It is not known if this inequality is ever strict. This is analogous to the question of whether or not trisection genus is additive under connected sum.
Example 3.29 Figure 12 lists the minimum complexities of some relative trisections and pseudo-trisections. It demonstrates that even for simple 4-manifolds complexities of relative trisections tend to be much greater than the lower bound given in Proposition 3.27. On the other hand, complexities of pseudo-trisections appear to be equal to
![]() $\beta _1 + \beta _2$
. This suggests that relative trisections tend to have significantly higher complexity than pseudo-trisections.
$\beta _1 + \beta _2$
. This suggests that relative trisections tend to have significantly higher complexity than pseudo-trisections.
The five (minimal) pseudo-trisections in Figure 12 are presented in Examples 3.12, 3.13, 3.14, and 3.15 and below in Figure 13. Since any pseudo-trisection with complexity
![]() $0$
is the trivial pseudo-trisection, it is automatic that the given pseudo-trisections for
$0$
is the trivial pseudo-trisection, it is automatic that the given pseudo-trisections for
![]() $S^1\times B^3$
and
$S^1\times B^3$
and
![]() $S^2\times D^2$
must be minimal. Next, one can see that any pseudo-trisection with complexity
$S^2\times D^2$
must be minimal. Next, one can see that any pseudo-trisection with complexity
![]() $1$
must have boundary a lens space or
$1$
must have boundary a lens space or
![]() $S^1\times S^2$
. It follows that the given pseudo-trisection for
$S^1\times S^2$
. It follows that the given pseudo-trisection for
![]() $(S^2\times D^2)\natural (S^2\times D^2)$
is also minimal. Another minimal pseudo-trisection of
$(S^2\times D^2)\natural (S^2\times D^2)$
is also minimal. Another minimal pseudo-trisection of
![]() $(S^2\times D^2)\natural (S^2\times D^2)$
is given by the boundary connected sum of a complexity 1 pseudo-trisection with itself.
$(S^2\times D^2)\natural (S^2\times D^2)$
is given by the boundary connected sum of a complexity 1 pseudo-trisection with itself.

Figure 12: Complexities of some simple 4-manifolds. When not known, the interval of possibilities is written.

Figure 13: A pseudo-trisection diagram of
![]() $(S^2\times D^2) \natural (S^2\times D^2)$
.
$(S^2\times D^2) \natural (S^2\times D^2)$
.
For relative trisections, it is again clear that the trivial trisection of
![]() $B^4$
is minimal, and any other trisection has complexity at least
$B^4$
is minimal, and any other trisection has complexity at least
![]() $1$
. Therefore the relative trisection given in Example 3.15 is minimal. Any relative trisection with complexity
$1$
. Therefore the relative trisection given in Example 3.15 is minimal. Any relative trisection with complexity
![]() $1$
must have boundary
$1$
must have boundary
![]() $S^3$
. It follows that a relative trisection of
$S^3$
. It follows that a relative trisection of
![]() $S^1\times B^3$
with complexity
$S^1\times B^3$
with complexity
![]() $2$
would be minimal. Such a relative trisection exists—it is prescribed by the relative trisection diagram consisting of an annulus (and no curves). Moreover, this is the only relative trisection with complexity
$2$
would be minimal. Such a relative trisection exists—it is prescribed by the relative trisection diagram consisting of an annulus (and no curves). Moreover, this is the only relative trisection with complexity
![]() $2$
and boundary not a sphere, as can be seen by enumerating diagrams.
$2$
and boundary not a sphere, as can be seen by enumerating diagrams.
From here, it follows that any relative trisection of
![]() $S^2\times D^2$
with complexity 3 must be minimal. However, the author could not find such an example, or rule out its existence. To the author’s best knowledge, the smallest known relative trisection of
$S^2\times D^2$
with complexity 3 must be minimal. However, the author could not find such an example, or rule out its existence. To the author’s best knowledge, the smallest known relative trisection of
![]() $S^2\times D^2$
has complexity 4—see [Reference A. Castro and Ozbagci3, Example 2.9].
$S^2\times D^2$
has complexity 4—see [Reference A. Castro and Ozbagci3, Example 2.9].
Finally, one can show again by enumerating diagrams that any relative trisection of
![]() $(S^2\times D^2) \natural (S^2\times D^2)$
must have complexity at least
$(S^2\times D^2) \natural (S^2\times D^2)$
must have complexity at least
![]() $4$
. To the author’s best knowledge, the smallest known relative trisection of
$4$
. To the author’s best knowledge, the smallest known relative trisection of
![]() $(S^2\times D^2)\natural (S^2\times D^2)$
has complexity 8, by taking the “plumbing” of a relative trisection of
$(S^2\times D^2)\natural (S^2\times D^2)$
has complexity 8, by taking the “plumbing” of a relative trisection of
![]() $S^2\times D^2$
with itself (in the sense of [Reference Castro, Islambouli, Miller and Tomova6, Theorem 3.20]). Note that it is not known whether or not relative trisection genus (equivalently, complexity) is additive under boundary connected sum [1].
$S^2\times D^2$
with itself (in the sense of [Reference Castro, Islambouli, Miller and Tomova6, Theorem 3.20]). Note that it is not known whether or not relative trisection genus (equivalently, complexity) is additive under boundary connected sum [1].
Example 3.30 For pseudo-trisections,
![]() $c(\natural ^\ell (S^2\times D^2)) \leq \ell $
. This is because we can iteratively take the boundary connected sum of the complexity 1 pseudo-trisection in Example 3.14 with itself, and complexity is subadditive. On the other hand, restricting to relative trisections and assuming additivity of relative trisection genus,
$c(\natural ^\ell (S^2\times D^2)) \leq \ell $
. This is because we can iteratively take the boundary connected sum of the complexity 1 pseudo-trisection in Example 3.14 with itself, and complexity is subadditive. On the other hand, restricting to relative trisections and assuming additivity of relative trisection genus,
![]() $c(\natural ^\ell (S^2\times D^2)) \geq 3\ell $
by Example 3.29.
$c(\natural ^\ell (S^2\times D^2)) \geq 3\ell $
by Example 3.29.
Remark 3.31 In Examples 3.29 and 3.30, we reference the question of whether or not relative trisection genus is additive under boundary connected sum. Evidence for the additivity of relative trisection genus is presented in a recent preprint of Takahashi [Reference Takahashi26]. Note that additivity of relative trisection genus would imply additivity of (closed) trisection genus, which in turn implies the Smooth Poincaré conjecture in dimension 4 [Reference Lambert-Cole and Meier14].
Remark 3.32 The author is unaware of manifolds X for which
![]() $c(X) < \beta _1 + \beta _2$
or
$c(X) < \beta _1 + \beta _2$
or
![]() $c(X,\partial X) = \beta _1 + \beta _2, c(\partial X)> 0$
. It appears likely that the bound given in Proposition 3.27 for pseudo-trisections can be improved.
$c(X,\partial X) = \beta _1 + \beta _2, c(\partial X)> 0$
. It appears likely that the bound given in Proposition 3.27 for pseudo-trisections can be improved.
Remark 3.33 To better measure the extent to which pseudo-trisections have lower complexity than relative trisections, we would need a sufficiently tight upper bound on the complexity of pseudo-trisections. This corresponds to further refining existence results in a way which is not done here.
3.7 Classification of low complexity pseudo-trisections
In this subsection, we determine which 4-manifolds admit pseudo-trisections with complexity at most 1. Consequently, we show that additivity of pseudo-trisection complexity under boundary connected sum would imply that disk bundles over
![]() $S^2$
are standard. We start by recalling a similar result in the closed setting.
$S^2$
are standard. We start by recalling a similar result in the closed setting.
Proposition 3.34 (Meier–Lambert–Cole, [Reference Lambert-Cole and Meier14, Proposition 1.7])
If trisection genus is additive under connected sum, then there is no exotic
![]() $S^4, \mathbb {CP}^2, S^1\times S^3, S^2\times S^2, \mathbb {CP}^2\#\mathbb {CP}^2$
, nor
$S^4, \mathbb {CP}^2, S^1\times S^3, S^2\times S^2, \mathbb {CP}^2\#\mathbb {CP}^2$
, nor
![]() $\mathbb {CP}^2\# \overline {\mathbb {CP}}{}^2$
.
$\mathbb {CP}^2\# \overline {\mathbb {CP}}{}^2$
.
If trisection genus is additive, a theorem of Wall [Reference Wall27] implies that trisection genus is a homeomorphism invariant of smooth manifolds. It remains to classify the closed 4-manifolds of given trisection genera, and indeed the above list corresponds to those with trisection genera at most 2.
Proposition 3.35 Let X be a compact connected oriented smooth 4-manifold with one boundary component.
-
• If
 $c(X) = 0$
, then X is
$c(X) = 0$
, then X is
 $B^4$
. Conversely,
$B^4$
. Conversely,
 $B^4$
admits a unique pseudo-trisection up to diffeomorphism with complexity 0.
$B^4$
admits a unique pseudo-trisection up to diffeomorphism with complexity 0. -
• If
 $c(X) = 1$
, then X is either
$c(X) = 1$
, then X is either
 $B^4, \mathbb {CP}^2 - B^4, S^1 \times B^3$
, or a disk bundle over
$B^4, \mathbb {CP}^2 - B^4, S^1 \times B^3$
, or a disk bundle over
 $S^2$
. Conversely, each of these manifolds admits a unique pseudo-trisection up to diffeomorphism with complexity 1.
$S^2$
. Conversely, each of these manifolds admits a unique pseudo-trisection up to diffeomorphism with complexity 1.
Proof The proof structure is to determine all possible pseudo-trisection diagrams with complexity 0 or 1 up to handleslides and isotopies. This proof depends on Section 4 and in particular Lemma 4.6, but we have placed it here for thematic reasons.
It is immediate that a pseudo-trisection with complexity
![]() $0$
is the trivial pseudo-trisection.
$0$
is the trivial pseudo-trisection.
Next, suppose X is pseudo-trisected with complexity
![]() $1$
. By Proposition 3.27,
$1$
. By Proposition 3.27,
![]() $b=1$
is fixed, and exactly one of
$b=1$
is fixed, and exactly one of
![]() $\Sigma _C, \Sigma _1, \Sigma _2, \Sigma _3$
has genus 1 while the rest are disks.
$\Sigma _C, \Sigma _1, \Sigma _2, \Sigma _3$
has genus 1 while the rest are disks.
Case 1:
![]() $\Sigma _C$
has genus 1, and each
$\Sigma _C$
has genus 1, and each
![]() $\Sigma _i$
is a disk. Then identifying the boundary of X with the boundary of a trivially trisected
$\Sigma _i$
is a disk. Then identifying the boundary of X with the boundary of a trivially trisected
![]() $B^4$
produces a trisection of a closed manifold with trisection genus 1. By [Reference Gay and Kirby7] this trisection is the unique trisection of
$B^4$
produces a trisection of a closed manifold with trisection genus 1. By [Reference Gay and Kirby7] this trisection is the unique trisection of
![]() $\mathbb {CP}^2$
up to diffeomorphism, and consequently X is
$\mathbb {CP}^2$
up to diffeomorphism, and consequently X is
![]() $\mathbb {CP}^2 - B^4$
, also trisected up to diffeomorphism with complexity
$\mathbb {CP}^2 - B^4$
, also trisected up to diffeomorphism with complexity
![]() $1$
.
$1$
.
Case 2: Without loss of generality,
![]() $\Sigma _1$
has genus 1, and each of
$\Sigma _1$
has genus 1, and each of
![]() $\Sigma _C, \Sigma _2, \Sigma _3$
is a disk. Then there is a pseudo-trisection diagram of the pseudo-trisection of X consisting of three simple closed curves
$\Sigma _C, \Sigma _2, \Sigma _3$
is a disk. Then there is a pseudo-trisection diagram of the pseudo-trisection of X consisting of three simple closed curves
![]() $\alpha _1, \delta _1, \delta _3$
on
$\alpha _1, \delta _1, \delta _3$
on
![]() $\Sigma _1$
. The triple Heegaard diagrams
$\Sigma _1$
. The triple Heegaard diagrams
![]() $(\Sigma _C, \Sigma _3,\Sigma _1,\varnothing , \delta _3,\alpha _1)$
and
$(\Sigma _C, \Sigma _3,\Sigma _1,\varnothing , \delta _3,\alpha _1)$
and
![]() $(\Sigma _C, \Sigma _1, \Sigma _2, \alpha _1, \delta _1, \varnothing )$
must encode either
$(\Sigma _C, \Sigma _1, \Sigma _2, \alpha _1, \delta _1, \varnothing )$
must encode either
![]() $S^3$
or
$S^3$
or
![]() $S^1\times S^2$
, which corresponds to the intersection numbers
$S^1\times S^2$
, which corresponds to the intersection numbers
![]() $\alpha _1 \cdot \delta _1$
and
$\alpha _1 \cdot \delta _1$
and
![]() $\delta _3 \cdot \alpha _1$
being
$\delta _3 \cdot \alpha _1$
being
![]() $0$
or
$0$
or
![]() $1$
.
$1$
.
Suppose
![]() $\alpha _1 \cdot \delta _1 = 0$
and
$\alpha _1 \cdot \delta _1 = 0$
and
![]() $\delta _3 \cdot \alpha _1 = 0$
. Then the resulting pseudo-trisection is of
$\delta _3 \cdot \alpha _1 = 0$
. Then the resulting pseudo-trisection is of
![]() $S^1\times B^3$
, described in Example 3.13. Suppose
$S^1\times B^3$
, described in Example 3.13. Suppose
![]() $\alpha _1\cdot \delta _1 = 0$
and
$\alpha _1\cdot \delta _1 = 0$
and
![]() $\delta _3 \cdot \alpha _1 = 1$
. Then
$\delta _3 \cdot \alpha _1 = 1$
. Then
![]() $\delta _3 \cdot \delta _1 = 1$
, and the resulting trisection is the Heegaard stabilization of the trivial trisection of
$\delta _3 \cdot \delta _1 = 1$
, and the resulting trisection is the Heegaard stabilization of the trivial trisection of
![]() $B^4$
. This is diffeomorphic to the trisection obtained when
$B^4$
. This is diffeomorphic to the trisection obtained when
![]() $\alpha _1 \cdot \delta _1 = 1$
and
$\alpha _1 \cdot \delta _1 = 1$
and
![]() $\delta _3 \cdot \alpha _1 = 0$
. Finally, suppose
$\delta _3 \cdot \alpha _1 = 0$
. Finally, suppose
![]() $\alpha _1 \cdot \delta _1$
and
$\alpha _1 \cdot \delta _1$
and
![]() $\delta _3 \cdot \alpha _1$
are both
$\delta _3 \cdot \alpha _1$
are both
![]() $1$
. Then
$1$
. Then
![]() $\delta _3 \cdot \delta _1 = e$
for any integer e, and for each e there is a unique configuration of
$\delta _3 \cdot \delta _1 = e$
for any integer e, and for each e there is a unique configuration of
![]() $\alpha _1, \delta _1, \delta _3$
on
$\alpha _1, \delta _1, \delta _3$
on
![]() $\Sigma _1$
(up to handleslides and isotopies) achieving the given intersections. Each such diagram encodes the disk bundle over
$\Sigma _1$
(up to handleslides and isotopies) achieving the given intersections. Each such diagram encodes the disk bundle over
![]() $S^2$
of Euler number e. In particular, when
$S^2$
of Euler number e. In particular, when
![]() $e=0$
, the corresponding pseudo-trisection is of
$e=0$
, the corresponding pseudo-trisection is of
![]() $S^2\times B^2$
, described in Example 3.14.
$S^2\times B^2$
, described in Example 3.14.
Remark 3.36 To the best of the author’s knowledge, there is currently no (non-trivial) list of the “simplest relative trisections”.
Corollary 3.37 If complexity of pseudo-trisections is additive under boundary connected sum, then there is no exotic
![]() $B^4$
,
$B^4$
,
![]() $\mathbb {CP}^2 - B^4$
,
$\mathbb {CP}^2 - B^4$
,
![]() $S^1\times B^3$
, or disk bundle over
$S^1\times B^3$
, or disk bundle over
![]() $S^2$
.
$S^2$
.
Proof By Gompf’s generalization of Wall’s theorem [Reference Gompf8, Reference Wall27], for any two homeomorphic compact oriented smooth 4-manifolds
![]() $X, X'$
, there exists an integer k such that
$X, X'$
, there exists an integer k such that
![]() $X \natural ^k (S^2\times S^2 - B^4)$
and
$X \natural ^k (S^2\times S^2 - B^4)$
and
![]() $X'\natural ^k (S^2\times S^2 - B^4)$
are diffeomorphic. Additivity of complexity would then imply that
$X'\natural ^k (S^2\times S^2 - B^4)$
are diffeomorphic. Additivity of complexity would then imply that
![]() $c(X) = c(X')$
, but Proposition 3.35 lists all manifolds with complexity at most 1, and the list contains no exotic pairs.
$c(X) = c(X')$
, but Proposition 3.35 lists all manifolds with complexity at most 1, and the list contains no exotic pairs.
Note that the existence of an exotic
![]() $B^4$
and
$B^4$
and
![]() $\mathbb {CP}^2 - B^4$
is equivalent to the existence of an exotic
$\mathbb {CP}^2 - B^4$
is equivalent to the existence of an exotic
![]() $S^4$
and
$S^4$
and
![]() $\mathbb {CP}^2$
.
$\mathbb {CP}^2$
.
4 Pseudo-trisection diagrams
In this section, we introduce pseudo-trisection diagrams. These represent pseudo-trisections in the same way that trisection diagrams represent relative trisections. We establish a one-to-one correspondence between pseudo-trisections diagrams (up to diagram moves) and pseudo-trisections (up to stabilization). We also use pseudo-trisection diagrams to prove Theorem 1.1, namely that for any 4-manifold with a given trisection of the boundary, there exists a pseudo-trisection of the 4-manifold extending the boundary trisection. Finally we describe some orientation conventions.
4.1 Pseudo-trisection diagrams
In this subsection, we introduce pseudo-trisection diagrams, which are diagrams for pseudo-trisections extended from triple Heegaard diagrams (in the same fashion that trisection diagrams are extended from Heegaard diagrams). A pseudo-trisection diagram consists of several arcs and closed curves on four surfaces, so that restricting to any three surfaces (and correspondingly coloured arcs) produces a triple Heegaard diagram. This is analogous to trisection diagrams consisting of three simultaneous Heegaard diagrams.
Definition 4.1 A
![]() $(g, \boldsymbol k, \boldsymbol y, b)$
-pseudo-trisection diagram consists of the data
$(g, \boldsymbol k, \boldsymbol y, b)$
-pseudo-trisection diagram consists of the data
![]() $(\Sigma _C, \Sigma _1, \Sigma _2, \Sigma _3, \boldsymbol \alpha _1, \boldsymbol \alpha _2, \boldsymbol \alpha _3, \boldsymbol \delta _{1}, \boldsymbol \delta _{2}, \boldsymbol \delta _{3})$
, with the following constraints.
$(\Sigma _C, \Sigma _1, \Sigma _2, \Sigma _3, \boldsymbol \alpha _1, \boldsymbol \alpha _2, \boldsymbol \alpha _3, \boldsymbol \delta _{1}, \boldsymbol \delta _{2}, \boldsymbol \delta _{3})$
, with the following constraints.
-
(1) Each
 $\Sigma _{\circ }$
,
$\Sigma _{\circ }$
,
 $\circ \in \{C, 1, 2, 3\}$
is a surface with boundary. Specifically,
$\circ \in \{C, 1, 2, 3\}$
is a surface with boundary. Specifically,
 $\Sigma _C$
has genus g and b boundary components, while
$\Sigma _C$
has genus g and b boundary components, while
 $\Sigma _i$
has genus
$\Sigma _i$
has genus
 $p_i = \frac {1}{2}(y_{i-1}+y_i - y_{i+1} - b + 1)$
and b boundary components.
$p_i = \frac {1}{2}(y_{i-1}+y_i - y_{i+1} - b + 1)$
and b boundary components. -
(2) There is an identification of the boundaries of all four of the
 $\Sigma _{\circ }$
. In particular,
$\Sigma _{\circ }$
. In particular,
 $\Sigma _i \cup \Sigma _{i+1}$
is a closed surface of genus
$\Sigma _i \cup \Sigma _{i+1}$
is a closed surface of genus
 $y_i$
, and
$y_i$
, and
 $\Sigma _C \cup \Sigma _i$
is a closed surface of genus
$\Sigma _C \cup \Sigma _i$
is a closed surface of genus
 $h_i = g + \frac {1}{2}(y_{i-1} + y_i - y_{i+1} + b - 1)$
.
$h_i = g + \frac {1}{2}(y_{i-1} + y_i - y_{i+1} + b - 1)$
. -
(3) Each
 $\boldsymbol \delta _i$
is a collection of disjoint neatly embedded arcs and simple closed curves on
$\boldsymbol \delta _i$
is a collection of disjoint neatly embedded arcs and simple closed curves on
 $\Sigma _i$
and
$\Sigma _i$
and
 $\Sigma _{i+1}$
, which glues to a cut system of
$\Sigma _{i+1}$
, which glues to a cut system of
 $y_i$
curves on
$y_i$
curves on
 $\Sigma _i \cup \Sigma _{i+1}$
. Similarly, each
$\Sigma _i \cup \Sigma _{i+1}$
. Similarly, each
 $\boldsymbol \alpha _i$
is a collection of disjoint neatly embedded arcs and simple closed curves on
$\boldsymbol \alpha _i$
is a collection of disjoint neatly embedded arcs and simple closed curves on
 $\Sigma _C$
and
$\Sigma _C$
and
 $\Sigma _i$
, which glues to a cut system of
$\Sigma _i$
, which glues to a cut system of
 $h_i$
curves on
$h_i$
curves on
 $\Sigma _C \cup \Sigma _i$
.
$\Sigma _C \cup \Sigma _i$
. -
(4) The data
are all triple Heegaard diagrams. Each of these three triple Heegaard diagrams encode $$ \begin{align*} &(\Sigma_C, \Sigma_1, \Sigma_2, \boldsymbol\alpha_1, \boldsymbol\delta_{1}, \boldsymbol\alpha_2)\\ &(\Sigma_C, \Sigma_2, \Sigma_3, \boldsymbol\alpha_2, \boldsymbol\delta_{2}, \boldsymbol\alpha_3)\\ &(\Sigma_C, \Sigma_3, \Sigma_1, \boldsymbol\alpha_3, \boldsymbol\delta_{3}, \boldsymbol\alpha_1) \end{align*} $$
$$ \begin{align*} &(\Sigma_C, \Sigma_1, \Sigma_2, \boldsymbol\alpha_1, \boldsymbol\delta_{1}, \boldsymbol\alpha_2)\\ &(\Sigma_C, \Sigma_2, \Sigma_3, \boldsymbol\alpha_2, \boldsymbol\delta_{2}, \boldsymbol\alpha_3)\\ &(\Sigma_C, \Sigma_3, \Sigma_1, \boldsymbol\alpha_3, \boldsymbol\delta_{3}, \boldsymbol\alpha_1) \end{align*} $$
 $\#^{k_i}S^1 \times S^2$
respectively.
$\#^{k_i}S^1 \times S^2$
respectively.
For notational brevity, we frequently write
![]() $(\Sigma _C,\Sigma _i, \boldsymbol \alpha _i,\boldsymbol \delta _i)$
instead of
$(\Sigma _C,\Sigma _i, \boldsymbol \alpha _i,\boldsymbol \delta _i)$
instead of
![]() $(\Sigma _C,\Sigma _1, \Sigma _2, \Sigma _3, \boldsymbol \alpha _1,\boldsymbol \alpha _2,\boldsymbol \alpha _3, \boldsymbol \delta _1,\boldsymbol \delta _2,\boldsymbol \delta _3)$
.
$(\Sigma _C,\Sigma _1, \Sigma _2, \Sigma _3, \boldsymbol \alpha _1,\boldsymbol \alpha _2,\boldsymbol \alpha _3, \boldsymbol \delta _1,\boldsymbol \delta _2,\boldsymbol \delta _3)$
.
Definition 4.2 There is a realization map
 $$ \begin{align*}\mathcal R: \{(g,\boldsymbol{k};\boldsymbol{y},b)\text{-pseudo-trisection diagrams}\} \to \frac{\{(g,\boldsymbol{k};\boldsymbol{y},b)\text{-pseudo-trisections}\}}{\text{diffeomorphism}}\end{align*} $$
$$ \begin{align*}\mathcal R: \{(g,\boldsymbol{k};\boldsymbol{y},b)\text{-pseudo-trisection diagrams}\} \to \frac{\{(g,\boldsymbol{k};\boldsymbol{y},b)\text{-pseudo-trisections}\}}{\text{diffeomorphism}}\end{align*} $$
defined as follows:
-
(1) First, glue the underlying surfaces
 $\Sigma _C, \Sigma _1, \Sigma _2, \Sigma _3$
along their common boundaries to obtain the 2-skeleton W.
$\Sigma _C, \Sigma _1, \Sigma _2, \Sigma _3$
along their common boundaries to obtain the 2-skeleton W. -
(2) Next, each pair of surfaces glues to a closed surface, and there is a corresponding cut system. (For example,
 $(\Sigma _C, \Sigma _2, \boldsymbol {\alpha }_2)$
.) Each cut system describes how to glue in a 3-dimensional 1-handlebody, as in the proof of Proposition 2.13. Gluing each of the six 3-dimensional 1-handlebodies produces the 3-skeleton Z.
$(\Sigma _C, \Sigma _2, \boldsymbol {\alpha }_2)$
.) Each cut system describes how to glue in a 3-dimensional 1-handlebody, as in the proof of Proposition 2.13. Gluing each of the six 3-dimensional 1-handlebodies produces the 3-skeleton Z. -
(3) By assumption, the diagrams
 $\mathcal {D}_1 = (\Sigma _C, \Sigma _1, \Sigma _2, \boldsymbol \alpha _1, \boldsymbol \delta _{1}, \boldsymbol \alpha _2)$
,
$\mathcal {D}_1 = (\Sigma _C, \Sigma _1, \Sigma _2, \boldsymbol \alpha _1, \boldsymbol \delta _{1}, \boldsymbol \alpha _2)$
,
 $\mathcal {D}_2 = (\Sigma _C, \Sigma _2, \Sigma _3, \boldsymbol \alpha _2, \boldsymbol \delta _{2}, \boldsymbol \alpha _3)$
, and
$\mathcal {D}_2 = (\Sigma _C, \Sigma _2, \Sigma _3, \boldsymbol \alpha _2, \boldsymbol \delta _{2}, \boldsymbol \alpha _3)$
, and
 $\mathcal {D}_3 = (\Sigma _C, \Sigma _3, \Sigma _1, \boldsymbol \alpha _3, \boldsymbol \delta _{3}, \boldsymbol \alpha _1)$
are each triple Heegaard diagrams of
$\mathcal {D}_3 = (\Sigma _C, \Sigma _3, \Sigma _1, \boldsymbol \alpha _3, \boldsymbol \delta _{3}, \boldsymbol \alpha _1)$
are each triple Heegaard diagrams of
 $\#^{k_i}(S^1\times S^2)$
. These bound 4-dimensional 1-handlebodies, which are labeled
$\#^{k_i}(S^1\times S^2)$
. These bound 4-dimensional 1-handlebodies, which are labeled
 $X_1, X_2$
, and
$X_1, X_2$
, and
 $X_3$
, respectively, and are precisely the sectors of a pseudo-trisection.
$X_3$
, respectively, and are precisely the sectors of a pseudo-trisection.
Proposition 4.3 The realization map
![]() $\mathcal R$
is well defined in the sense that any two pseudo-trisections constructed by the definition of
$\mathcal R$
is well defined in the sense that any two pseudo-trisections constructed by the definition of
![]() $\mathcal R$
are indeed diffeomorphic.
$\mathcal R$
are indeed diffeomorphic.
Proof Suppose X and
![]() $X'$
are pseudo-trisected 4-manifolds constructed from a given pseudo-trisection diagram by
$X'$
are pseudo-trisected 4-manifolds constructed from a given pseudo-trisection diagram by
![]() $\mathcal R$
. Let
$\mathcal R$
. Let
![]() $X_i$
and
$X_i$
and
![]() $X_i'$
be the sectors, W and
$X_i'$
be the sectors, W and
![]() $W'$
the 2-skeleta, and Z and
$W'$
the 2-skeleta, and Z and
![]() $Z'$
be the 3-skeleta of X and
$Z'$
be the 3-skeleta of X and
![]() $X'$
respectively. Notice that the 2-skeleta are exactly the union of the surfaces in the pseudo-trisection diagram, so we start with the identity map
$X'$
respectively. Notice that the 2-skeleta are exactly the union of the surfaces in the pseudo-trisection diagram, so we start with the identity map
![]() $W \to W'$
. Next, we extend this to a map
$W \to W'$
. Next, we extend this to a map
![]() $Z \to Z'$
by (the proof of) Proposition 2.13. This map restricts to diffeomorphisms
$Z \to Z'$
by (the proof of) Proposition 2.13. This map restricts to diffeomorphisms
![]() $\partial X_i \to \partial X_i'$
as trisected 3-manifolds. Finally, we apply a theorem of Laudenbach and Poénaru [Reference Laudenbach and Poénaru15] which states that diffeomorphisms of
$\partial X_i \to \partial X_i'$
as trisected 3-manifolds. Finally, we apply a theorem of Laudenbach and Poénaru [Reference Laudenbach and Poénaru15] which states that diffeomorphisms of
![]() $\#k(S^1\times S^2)$
extend to diffeomorphisms of
$\#k(S^1\times S^2)$
extend to diffeomorphisms of
![]() $\natural ^k(S^1\times B^3)$
. Namely, the diffeomorphisms
$\natural ^k(S^1\times B^3)$
. Namely, the diffeomorphisms
![]() $\partial X_i \to \partial X_i'$
above each extend to maps
$\partial X_i \to \partial X_i'$
above each extend to maps
![]() $X_i \to X^{\prime }_i$
. These three extensions glue along Z to give a diffeomorphism
$X_i \to X^{\prime }_i$
. These three extensions glue along Z to give a diffeomorphism
![]() $X \to X'$
.
$X \to X'$
.
Example 4.4 Figure 13 is an example of a pseudo-trisection diagram, namely of
![]() $(S^2\times D^2) \natural (S^2\times D^2)$
. Restricting the diagram to
$(S^2\times D^2) \natural (S^2\times D^2)$
. Restricting the diagram to
![]() $(\Sigma _1, \Sigma _2, \Sigma _3, \delta _1, \delta _2, \delta _3)$
produces exactly the triple Heegaard diagram of
$(\Sigma _1, \Sigma _2, \Sigma _3, \delta _1, \delta _2, \delta _3)$
produces exactly the triple Heegaard diagram of
![]() $(S^1\times S^2)\# (S^1\times S^2)$
shown in Figure 8. On the other hand, the other triple Heegaard diagrams such as
$(S^1\times S^2)\# (S^1\times S^2)$
shown in Figure 8. On the other hand, the other triple Heegaard diagrams such as
![]() $(\Sigma _C, \Sigma _1, \Sigma _2, \alpha _1, \delta _1, \alpha _2)$
each describe
$(\Sigma _C, \Sigma _1, \Sigma _2, \alpha _1, \delta _1, \alpha _2)$
each describe
![]() $S^1\times S^2$
, so this is a valid pseudo-trisection diagram. One can show that the diagram really does encode
$S^1\times S^2$
, so this is a valid pseudo-trisection diagram. One can show that the diagram really does encode
![]() $(S^2\times D^2)\natural (S^2\times D^2)$
by applying the realization map.
$(S^2\times D^2)\natural (S^2\times D^2)$
by applying the realization map.
Example 4.5 Figure 14 depicts several of the simplest pseudo-trisection diagrams, by using the same choice of
![]() $\Sigma _C, \Sigma _2$
, and
$\Sigma _C, \Sigma _2$
, and
![]() $\Sigma _3$
, but switching out
$\Sigma _3$
, but switching out
![]() $\Sigma _1$
and the associated curves.
$\Sigma _1$
and the associated curves.
 $$ \begin{align*} (\Sigma_C, \Sigma_1, \Sigma_2, \Sigma_3, \varnothing, \varnothing, \varnothing, \varnothing, \varnothing, \varnothing) &\longrightarrow B^4,\\ (\Sigma_C, \Sigma_1', \Sigma_2, \Sigma_3, \alpha_1, \varnothing, \varnothing, \delta_1, \varnothing, \delta_3) &\longrightarrow S^1\times B^3,\\ (\Sigma_C, \Sigma_1", \Sigma_2, \Sigma_3, \alpha_1^*, \varnothing, \varnothing, \delta_1, \varnothing, \delta_3) &\longrightarrow S^2\times B^2. \end{align*} $$
$$ \begin{align*} (\Sigma_C, \Sigma_1, \Sigma_2, \Sigma_3, \varnothing, \varnothing, \varnothing, \varnothing, \varnothing, \varnothing) &\longrightarrow B^4,\\ (\Sigma_C, \Sigma_1', \Sigma_2, \Sigma_3, \alpha_1, \varnothing, \varnothing, \delta_1, \varnothing, \delta_3) &\longrightarrow S^1\times B^3,\\ (\Sigma_C, \Sigma_1", \Sigma_2, \Sigma_3, \alpha_1^*, \varnothing, \varnothing, \delta_1, \varnothing, \delta_3) &\longrightarrow S^2\times B^2. \end{align*} $$
In fact, these three diagrams are precisely the diagrams giving rise to the pseudo-trisections in Examples 3.12, 3.13, and 3.14.

Figure 14: Three pseudo-trisection diagrams (arising from three different choices of
![]() $\Sigma _1$
).
$\Sigma _1$
).
Lemma 4.6 Fix a pseudo-trisection
![]() $\mathcal T$
of X. Any two pseudo-trisection diagrams
$\mathcal T$
of X. Any two pseudo-trisection diagrams
![]() $\mathcal D$
and
$\mathcal D$
and
![]() $\mathcal D'$
with realization
$\mathcal D'$
with realization
![]() $\mathcal T$
are diffeomorphic after a sequence of handleslides and isotopies. (That is, there are diffeomorphisms
$\mathcal T$
are diffeomorphic after a sequence of handleslides and isotopies. (That is, there are diffeomorphisms
![]() $\varphi _\circ : \Sigma _\circ \to \Sigma _\circ '$
rel boundary preserving the arcs on the surfaces.)
$\varphi _\circ : \Sigma _\circ \to \Sigma _\circ '$
rel boundary preserving the arcs on the surfaces.)
Proof This essentially follows from the proof of Lemma 2.21. For each sector
![]() $Y_i$
or
$Y_i$
or
![]() $H_i$
of the trisection, the corresponding meridian system (considered up to isotopy) [Reference Johannson11] is unique up to handleslides. A pseudo-trisection diagram is a collection of six overlapping meridian systems.
$H_i$
of the trisection, the corresponding meridian system (considered up to isotopy) [Reference Johannson11] is unique up to handleslides. A pseudo-trisection diagram is a collection of six overlapping meridian systems.
Note that handleslides and isotopies of pseudo-trisections are identical to those of triple Heegaard diagrams, described in Example 2.20.
Next we give diagrammatic descriptions of boundary stabilization, Heegaard stabilization, and internal stabilization. At the diagrammatic level, we find that Heegaard stabilization and internal stabilization fit into the same framework, which we call torus stabilization.
Definition 4.7 Given a pseudo-trisection diagram, a torus stabilization is a new pseudo-trisection diagram obtained by increasing the genus of one of the
![]() $\Sigma _i$
or
$\Sigma _i$
or
![]() $\Sigma _C$
by 1, and correspondingly adding three curves as shown in Figure 15. There are two types, as follows:
$\Sigma _C$
by 1, and correspondingly adding three curves as shown in Figure 15. There are two types, as follows:
-
• Type I. Let
 $T^2$
be a torus with three curves, namely two meridians
$T^2$
be a torus with three curves, namely two meridians
 $\mu _1, \mu _2$
and a longitude
$\mu _1, \mu _2$
and a longitude
 $\gamma $
. For a fixed
$\gamma $
. For a fixed
 $j \in \{1,2,3\}$
, a type I torus stabilization of
$j \in \{1,2,3\}$
, a type I torus stabilization of
 $(\Sigma _C, \Sigma _i, \boldsymbol \alpha _i, \boldsymbol \delta _{i})$
is the diagram obtained by replacing
$(\Sigma _C, \Sigma _i, \boldsymbol \alpha _i, \boldsymbol \delta _{i})$
is the diagram obtained by replacing
 $\Sigma _j$
with
$\Sigma _j$
with
 $\Sigma _j \# T^2$
,
$\Sigma _j \# T^2$
,
 $\boldsymbol \alpha _j$
with
$\boldsymbol \alpha _j$
with
 $\boldsymbol \alpha _j \cup \{\mu _1\}$
,
$\boldsymbol \alpha _j \cup \{\mu _1\}$
,
 $\boldsymbol \delta _{j-1}$
with
$\boldsymbol \delta _{j-1}$
with
 $\boldsymbol \delta _{j-1}\cup \{\mu _2\}$
, and
$\boldsymbol \delta _{j-1}\cup \{\mu _2\}$
, and
 $\boldsymbol \delta _j$
with
$\boldsymbol \delta _j$
with
 $\boldsymbol \delta _j \cup \{\gamma \}$
.
$\boldsymbol \delta _j \cup \{\gamma \}$
. -
• Type II. Let
 $(T^2, \mu _1, \mu _2, \gamma )$
be as above. For a fixed
$(T^2, \mu _1, \mu _2, \gamma )$
be as above. For a fixed
 $j \in \{1, 2, 3\}$
, a type II torus stabilization of
$j \in \{1, 2, 3\}$
, a type II torus stabilization of
 $(\Sigma _C, \Sigma _i, \boldsymbol \alpha _i, \boldsymbol \delta _{i})$
is the diagram obtained by replacing
$(\Sigma _C, \Sigma _i, \boldsymbol \alpha _i, \boldsymbol \delta _{i})$
is the diagram obtained by replacing
 $\Sigma _C$
with
$\Sigma _C$
with
 $\Sigma _C \# T^2$
,
$\Sigma _C \# T^2$
,
 $\boldsymbol \alpha _j$
with
$\boldsymbol \alpha _j$
with
 $\boldsymbol \alpha _j \cup \{\gamma \}$
,
$\boldsymbol \alpha _j \cup \{\gamma \}$
,
 $\boldsymbol \alpha _{j+1}$
with
$\boldsymbol \alpha _{j+1}$
with
 $\boldsymbol \alpha _{j+1}\cup \{\mu _1\}$
, and
$\boldsymbol \alpha _{j+1}\cup \{\mu _1\}$
, and
 $\boldsymbol \alpha _{j-1}$
with
$\boldsymbol \alpha _{j-1}$
with
 $\boldsymbol \alpha _{j-1} \cup \{\mu _2\}$
.
$\boldsymbol \alpha _{j-1} \cup \{\mu _2\}$
.

Figure 15: An example of a torus stabilization (which is type II with the given labels). See Definition 4.7.
One can check that torus stabilization is well defined by observing that the result of torus stabilization is a valid pseudo-trisection diagram, and moreover that it is a diagram of the same underlying 4-manifold.
Proposition 4.8 Torus stabilizations of pseudo-trisection diagrams correspond to Heegaard stabilizations and internal stabilizations of pseudo-trisections. More precisely, the following hold:
-
(1) Let
 $\mathcal D$
be a pseudo-trisection diagram with realization
$\mathcal D$
be a pseudo-trisection diagram with realization
 $\mathcal T$
. Let
$\mathcal T$
. Let
 $\mathcal D'$
be a type I torus stabilization of
$\mathcal D'$
be a type I torus stabilization of
 $\mathcal D$
. Then the realization of
$\mathcal D$
. Then the realization of
 $\mathcal D'$
is a Heegaard stabilization of
$\mathcal D'$
is a Heegaard stabilization of
 $\mathcal T$
.
$\mathcal T$
. -
(2) Let
 $\mathcal T'$
be a Heegaard stabilization of
$\mathcal T'$
be a Heegaard stabilization of
 $\mathcal T$
. Then there is a pseudo-trisection diagram
$\mathcal T$
. Then there is a pseudo-trisection diagram
 $\mathcal D$
such that its realization is
$\mathcal D$
such that its realization is
 $\mathcal T$
, and moreover a type I torus stabilization of
$\mathcal T$
, and moreover a type I torus stabilization of
 $\mathcal D$
has realization
$\mathcal D$
has realization
 $\mathcal T'$
.
$\mathcal T'$
. -
(3) Let
 $\mathcal D$
be a pseudo-trisection diagram with realization
$\mathcal D$
be a pseudo-trisection diagram with realization
 $\mathcal T$
. Let
$\mathcal T$
. Let
 $\mathcal D'$
be a type II torus stabilization of
$\mathcal D'$
be a type II torus stabilization of
 $\mathcal D$
. Then the realization of
$\mathcal D$
. Then the realization of
 $\mathcal D'$
is an internal stabilization of
$\mathcal D'$
is an internal stabilization of
 $\mathcal T$
.
$\mathcal T$
. -
(4) Let
 $\mathcal T'$
be an internal stabilization of
$\mathcal T'$
be an internal stabilization of
 $\mathcal T$
. Then there is a pseudo-trisection diagram
$\mathcal T$
. Then there is a pseudo-trisection diagram
 $\mathcal D$
such that its realization is
$\mathcal D$
such that its realization is
 $\mathcal T$
, and moreover a type II torus stabilization of
$\mathcal T$
, and moreover a type II torus stabilization of
 $\mathcal D$
has realization
$\mathcal D$
has realization
 $\mathcal T'$
.
$\mathcal T'$
.
Proof Item (1) is a direct consequence of the definition of realiation. Specifically, the connected sum of some
![]() $\Sigma _j$
with a torus results in the 3-dimensional 1-handlebodies
$\Sigma _j$
with a torus results in the 3-dimensional 1-handlebodies
![]() $H_j, Y_{j-1}$
, and
$H_j, Y_{j-1}$
, and
![]() $Y_j$
each gaining a handle
$Y_j$
each gaining a handle
![]() $h_{H_j}, h_{Y_{j-1}}$
, and
$h_{H_j}, h_{Y_{j-1}}$
, and
![]() $h_{Y_j}$
respectively. The curves added in the type I torus stabilization ensure that
$h_{Y_j}$
respectively. The curves added in the type I torus stabilization ensure that
![]() $h_{H_j}$
and
$h_{H_j}$
and
![]() $h_{Y_{j-1}}$
are parallel, while the other two pairs cancel. Gluing
$h_{Y_{j-1}}$
are parallel, while the other two pairs cancel. Gluing
![]() $H_j \cup h_{H_j}, Y_{j-1} \cup h_{Y_{j-1}}$
, and
$H_j \cup h_{H_j}, Y_{j-1} \cup h_{Y_{j-1}}$
, and
![]() $H_{j-1}$
, we obtain a 3-manifold differing from
$H_{j-1}$
, we obtain a 3-manifold differing from
![]() $\partial X_{j-1}$
by a connected sum with
$\partial X_{j-1}$
by a connected sum with
![]() $S^1\times S^2$
. This corresponds to the boundary of the handle attached in Heegaard stabilization.
$S^1\times S^2$
. This corresponds to the boundary of the handle attached in Heegaard stabilization.
To prove item (2) one can choose any pseudo-trisection diagram
![]() $\mathcal D$
of
$\mathcal D$
of
![]() $\mathcal T$
. The Heegaard stabilization involves an arc
$\mathcal T$
. The Heegaard stabilization involves an arc
![]() $\alpha $
in some
$\alpha $
in some
![]() $Y_j$
with endpoints
$Y_j$
with endpoints
![]() $p, q$
in
$p, q$
in
![]() $\Sigma _j$
, with neighborhood
$\Sigma _j$
, with neighborhood
![]() $N(\alpha ) \subset Y_j$
. Let
$N(\alpha ) \subset Y_j$
. Let
![]() $\gamma _1$
be the arc obtained by pushing
$\gamma _1$
be the arc obtained by pushing
![]() $\alpha $
to the boundary of
$\alpha $
to the boundary of
![]() $N(\alpha )$
, and
$N(\alpha )$
, and
![]() $\gamma _2$
the arc obtained by isotoping
$\gamma _2$
the arc obtained by isotoping
![]() $\alpha $
onto
$\alpha $
onto
![]() $\Sigma _j$
and pushing the endpoints to agree with
$\Sigma _j$
and pushing the endpoints to agree with
![]() $\gamma _1$
. Let
$\gamma _1$
. Let
![]() $\gamma $
be the closed curve
$\gamma $
be the closed curve
![]() $\gamma _1 \cup \gamma _2$
. Next, let
$\gamma _1 \cup \gamma _2$
. Next, let
![]() $\mu _1$
and
$\mu _1$
and
![]() $\mu _2$
be meridians of
$\mu _2$
be meridians of
![]() $N(\alpha )$
. Create the diagram
$N(\alpha )$
. Create the diagram
![]() $\mathcal D'$
by a surgery replacing disks around p and q with an annulus corresponding to the boundary of
$\mathcal D'$
by a surgery replacing disks around p and q with an annulus corresponding to the boundary of
![]() $N(\alpha )$
, and add new curves
$N(\alpha )$
, and add new curves
![]() $\gamma , \mu _1, \mu _2$
to the diagram as in the definition of type I torus stabilizations. After handleslides and isotopies of
$\gamma , \mu _1, \mu _2$
to the diagram as in the definition of type I torus stabilizations. After handleslides and isotopies of
![]() $\gamma $
, the resulting diagram is a type I torus stabilization of
$\gamma $
, the resulting diagram is a type I torus stabilization of
![]() $\mathcal D$
which has realiation
$\mathcal D$
which has realiation
![]() $\mathcal T'$
.
$\mathcal T'$
.
Items (3) and (4) are analogous to (1) and (2) and left to the reader.
Definition 4.9 Given a pseudo-trisection diagram, a band stabilization is a new pseudo-trisection diagram obtained by the following procedure:
-
(1) Identify a non-separating neatly embedded arc
 $\alpha $
in some
$\alpha $
in some
 $\Sigma _i$
. Thicken the arc to a band in
$\Sigma _i$
. Thicken the arc to a band in
 $\Sigma _i$
.
$\Sigma _i$
. -
(2) New surfaces
 $\Sigma _i', \Sigma _{i+1}', \Sigma _{i+2}', \Sigma _C'$
are obtained by subtracting the band in
$\Sigma _i', \Sigma _{i+1}', \Sigma _{i+2}', \Sigma _C'$
are obtained by subtracting the band in
 $\Sigma _i'$
, and attaching the band to the other three surfaces.
$\Sigma _i'$
, and attaching the band to the other three surfaces. -
(3) The preexisting curves on the surfaces are cut and pasted if they intersect the band, as shown by the change from
 $\delta _1$
to
$\delta _1$
to
 $\delta _1'$
in Figure 16. Three new curves are added, one to each of
$\delta _1'$
in Figure 16. Three new curves are added, one to each of
 $\boldsymbol {\delta }_{i+1}, \boldsymbol {\alpha }_{i+1}$
, and
$\boldsymbol {\delta }_{i+1}, \boldsymbol {\alpha }_{i+1}$
, and
 $\boldsymbol {\alpha }_{i+2}$
. Each curve consists of two arcs in the diagram, one in each corresponding surface. Each arc is a cocore of the attached band. See Figure 16 for a depiction of the case when
$\boldsymbol {\alpha }_{i+2}$
. Each curve consists of two arcs in the diagram, one in each corresponding surface. Each arc is a cocore of the attached band. See Figure 16 for a depiction of the case when
 $i = 1$
.
$i = 1$
.
Figure 16: An example of a band stabilisation. See Definition 4.9.
One can check that band stabilization is well defined by observing that the result is a pseudo-trisection diagram, and moreover that it is a diagram of the same underlying 4-manifold.
Proposition 4.10 Band stabilizations of pseudo-trisection diagrams correspond to boundary stabilizations of pseudo-trisections. More precisely, the following hold:
-
(1) Let
 $\mathcal D$
be a pseudo-trisection diagram with realization
$\mathcal D$
be a pseudo-trisection diagram with realization
 $\mathcal T$
. Let
$\mathcal T$
. Let
 $\mathcal D'$
be a band stabilization of
$\mathcal D'$
be a band stabilization of
 $\mathcal D$
. Then the realization of
$\mathcal D$
. Then the realization of
 $\mathcal D'$
is a boundary stabilization of
$\mathcal D'$
is a boundary stabilization of
 $\mathcal T$
.
$\mathcal T$
. -
(2) Let
 $\mathcal T'$
be a boundary stabilization of
$\mathcal T'$
be a boundary stabilization of
 $\mathcal T$
. Then there is a pseudo-trisection diagram
$\mathcal T$
. Then there is a pseudo-trisection diagram
 $\mathcal D$
such that its realization is
$\mathcal D$
such that its realization is
 $\mathcal T$
, and moreover a band stabilization of
$\mathcal T$
, and moreover a band stabilization of
 $\mathcal D$
has realization
$\mathcal D$
has realization
 $\mathcal T'$
.
$\mathcal T'$
.
Proof The proof is similar to the proof of Proposition 4.8. The equivalence is established by viewing the surfaces of the diagram as the 2-skeleton of the pseudo-trisection, and equating the arc
![]() $\alpha $
in the definition of band stabilization with the arc used in the definition of boundary stabilization.
$\alpha $
in the definition of band stabilization with the arc used in the definition of boundary stabilization.
Theorem 1.3 The realization map
 $$ \begin{align*}\mathcal R : \{\text{pseudo-trisection diagrams}\} \to \frac{\{\text{pseudo-trisections}\}}{\text{diffeomorphism}}\end{align*} $$
$$ \begin{align*}\mathcal R : \{\text{pseudo-trisection diagrams}\} \to \frac{\{\text{pseudo-trisections}\}}{\text{diffeomorphism}}\end{align*} $$
induces a bijection
 $$ \begin{align*}\frac{\Big\{\text{pseudo-trisection diagrams}\Big\}}{\begin{matrix}\text{band and torus stabilization,}\\ \text{handleslide, isotopy}\end{matrix}} \longrightarrow \frac{\Big\{\begin{matrix}\text{compact oriented 4-manifolds}\\ \text{with one boundary component}\end{matrix}\Big\}}{\text{diffeomorphism}}.\end{align*} $$
$$ \begin{align*}\frac{\Big\{\text{pseudo-trisection diagrams}\Big\}}{\begin{matrix}\text{band and torus stabilization,}\\ \text{handleslide, isotopy}\end{matrix}} \longrightarrow \frac{\Big\{\begin{matrix}\text{compact oriented 4-manifolds}\\ \text{with one boundary component}\end{matrix}\Big\}}{\text{diffeomorphism}}.\end{align*} $$
Proof This proof is analogous to that of Proposition 2.22. By Lemma 4.6, any two pseudo-trisection diagrams of a fixed pseudo-trisection are diffeomorphic after a sequence of handleslides and isotopies. By Theorem 1.2, any two pseudo-trisections of a given 4-manifold are equivalent up to boundary, Heegaard, and internal stabilization. By Propositions 4.10 and 4.8, band and torus stabilizations correspond to boundary, Heegaard, and internal stabilizations.
4.2 Boundary stabilization shift and relative existence
Boundary stabilization of pseudo-trisections is an extension of stabilization of 3-manifold trisections to the entire 4-manifold. In this subsection, we show that there is a reverse operation—destabilization of the boundary extends to the 4-manifold as well. We use this operation to establish that any trisection of the boundary 3-manifold of X extends to a pseudo-trisection of X. This mirrors the existence result for relative trisections [Reference Gay and Kirby7].
Definition 4.11 Boundary stabilization shift is an operation on pseudo-trisections with stabilized boundary defined diagrammatically in Figure 17 which can be thought of as exchanging a stabilization of the boundary for an internal stabilization. The details are as follows:
-
(1) Let X be equipped with a pseudo-trisection
 $\mathcal T$
such that
$\mathcal T$
such that
 $\mathcal T|_{\partial X}$
is a stabilisation of a trisection
$\mathcal T|_{\partial X}$
is a stabilisation of a trisection
 $\tau '$
of
$\tau '$
of
 $\partial X$
.
$\partial X$
. -
(2) Let
 $(\Sigma _C, \Sigma _i, \boldsymbol {\alpha }_i, \boldsymbol {\delta }_i)$
be a pseudo-trisection diagram of
$(\Sigma _C, \Sigma _i, \boldsymbol {\alpha }_i, \boldsymbol {\delta }_i)$
be a pseudo-trisection diagram of
 $\mathcal T$
realizing the stabilisation of the boundary. (This is the top row of Figure 17.) Locally, each of
$\mathcal T$
realizing the stabilisation of the boundary. (This is the top row of Figure 17.) Locally, each of
 $\Sigma _1, \Sigma _2$
, and
$\Sigma _1, \Sigma _2$
, and
 $\Sigma _3$
are as depicted by shading, but nothing can be said about how
$\Sigma _3$
are as depicted by shading, but nothing can be said about how
 $\Sigma _C$
meets its boundary.
$\Sigma _C$
meets its boundary. -
(3) The boundary stabilisation shift of
 $\mathcal T$
is the pseudo-trisection given by the diagram in the bottom row of Figure 17. This is obtained by band surgery on each of
$\mathcal T$
is the pseudo-trisection given by the diagram in the bottom row of Figure 17. This is obtained by band surgery on each of
 $\Sigma _i$
and
$\Sigma _i$
and
 $\Sigma _C$
: a band is glued to obtain each of
$\Sigma _C$
: a band is glued to obtain each of
 $\Sigma _1'$
and
$\Sigma _1'$
and
 $\Sigma _C'$
, with a corresponding meridian in
$\Sigma _C'$
, with a corresponding meridian in
 $\boldsymbol {\alpha }_1$
, and bands are deleted to obtain
$\boldsymbol {\alpha }_1$
, and bands are deleted to obtain
 $\Sigma _2'$
and
$\Sigma _2'$
and
 $\Sigma _3'$
.
$\Sigma _3'$
.

Figure 17: A diagrammatic definition of boundary stabilisation shift, see Definition 4.11.
Lemma 4.12 Boundary stabilisation shift is well defined.
Proof Referring back to Definition 4.1, being well defined requires that each
![]() $\boldsymbol {\delta }_i$
and
$\boldsymbol {\delta }_i$
and
![]() $\boldsymbol {\alpha }_i$
must be a cut system of its corresponding surface, and that each of the triple Heegaard diagrams induced on the three triples
$\boldsymbol {\alpha }_i$
must be a cut system of its corresponding surface, and that each of the triple Heegaard diagrams induced on the three triples
![]() $(\Sigma _C', \Sigma _i', \Sigma _{i+1}')$
are specifically diagrams of connected sums of
$(\Sigma _C', \Sigma _i', \Sigma _{i+1}')$
are specifically diagrams of connected sums of
![]() $S^1\times S^2$
.
$S^1\times S^2$
.
For the first condition, observe that the only surface-pairs whose unions have changed in the operation are
![]() $\Sigma _2' \cup \Sigma _3'$
and
$\Sigma _2' \cup \Sigma _3'$
and
![]() $\Sigma _1' \cup \Sigma _C'$
. In the former, the genus is decreased by a surgery along a neighborhood of
$\Sigma _1' \cup \Sigma _C'$
. In the former, the genus is decreased by a surgery along a neighborhood of
![]() $\gamma $
, so
$\gamma $
, so
![]() $\boldsymbol {\delta }_2 - \{\gamma \}$
is a cut system of
$\boldsymbol {\delta }_2 - \{\gamma \}$
is a cut system of
![]() $\Sigma _2' \cup \Sigma _3'$
. In the latter, the genus is increased and
$\Sigma _2' \cup \Sigma _3'$
. In the latter, the genus is increased and
![]() $\mu $
is the corresponding meridian, so
$\mu $
is the corresponding meridian, so
![]() $\boldsymbol {\alpha }_1 \cup \{\mu \}$
is a cut system.
$\boldsymbol {\alpha }_1 \cup \{\mu \}$
is a cut system.
For the second condition, we observe that
![]() $(\Sigma _C', \Sigma _1', \Sigma _2', \boldsymbol {\alpha }_1 \cup \{\mu \}, \boldsymbol {\delta }_1, \boldsymbol {\alpha }_2)$
is a stabilisation of
$(\Sigma _C', \Sigma _1', \Sigma _2', \boldsymbol {\alpha }_1 \cup \{\mu \}, \boldsymbol {\delta }_1, \boldsymbol {\alpha }_2)$
is a stabilisation of
![]() $(\Sigma _C, \Sigma _1, \Sigma _2, \boldsymbol {\alpha }_1, \boldsymbol {\delta }_1, \boldsymbol {\alpha }_2)$
. The latter is necessarily a diagram of
$(\Sigma _C, \Sigma _1, \Sigma _2, \boldsymbol {\alpha }_1, \boldsymbol {\delta }_1, \boldsymbol {\alpha }_2)$
. The latter is necessarily a diagram of
![]() $\#^{k_1}(S^1\times S^2)$
because our operation is on a valid pseudo-trisection diagram. Consequently,
$\#^{k_1}(S^1\times S^2)$
because our operation is on a valid pseudo-trisection diagram. Consequently,
![]() $(\Sigma _C', \Sigma _1', \Sigma _2', \boldsymbol {\alpha }_1\cup \{\mu \}, \boldsymbol {\delta }_1, \boldsymbol {\alpha }_2)$
is a diagram of
$(\Sigma _C', \Sigma _1', \Sigma _2', \boldsymbol {\alpha }_1\cup \{\mu \}, \boldsymbol {\delta }_1, \boldsymbol {\alpha }_2)$
is a diagram of
![]() $\#^{k_1}(S^1\times S^2)$
. Similarly,
$\#^{k_1}(S^1\times S^2)$
. Similarly,
![]() $(\Sigma _C', \Sigma _3', \Sigma _1', \boldsymbol {\alpha }_3, \boldsymbol {\delta }_3, \boldsymbol {\alpha }_1 \cup \{\mu \})$
is a diagram of
$(\Sigma _C', \Sigma _3', \Sigma _1', \boldsymbol {\alpha }_3, \boldsymbol {\delta }_3, \boldsymbol {\alpha }_1 \cup \{\mu \})$
is a diagram of
![]() $\#^{k_3}(S^1\times S^2)$
. The remaining check is that
$\#^{k_3}(S^1\times S^2)$
. The remaining check is that
![]() $(\Sigma _C', \Sigma _2', \Sigma _3', \boldsymbol {\alpha }_2, \boldsymbol {\delta }_2 \cup \{\gamma \}, \boldsymbol {\alpha }_3)$
is locally a destabilisation of
$(\Sigma _C', \Sigma _2', \Sigma _3', \boldsymbol {\alpha }_2, \boldsymbol {\delta }_2 \cup \{\gamma \}, \boldsymbol {\alpha }_3)$
is locally a destabilisation of
![]() $(\Sigma _C, \Sigma _2, \Sigma _3, \boldsymbol {\alpha }_2, \boldsymbol {\delta }_2, \boldsymbol {\alpha }_3)$
, so it is a diagram of
$(\Sigma _C, \Sigma _2, \Sigma _3, \boldsymbol {\alpha }_2, \boldsymbol {\delta }_2, \boldsymbol {\alpha }_3)$
, so it is a diagram of
![]() $\#^{k_2}(S^1\times S^2)$
.
$\#^{k_2}(S^1\times S^2)$
.
Proposition 4.13 Boundary stabilisation shift of
![]() $\mathcal T$
to
$\mathcal T$
to
![]() $\mathcal T'$
satisfies the following properties:
$\mathcal T'$
satisfies the following properties:
-
(1)
 $\mathcal T|_{\partial X}$
is a stabilisation of
$\mathcal T|_{\partial X}$
is a stabilisation of
 $\mathcal T'|_{\partial X}$
(in the sense of 3-manifold trisections).
$\mathcal T'|_{\partial X}$
(in the sense of 3-manifold trisections). -
(2) Complexity of the pseudo-trisection is invariant under boundary stabilisation shift, while complexity of the boundary decreases by 1.
-
(3) Suppose
 $\mathcal T$
is a boundary stabilisation of a pseudo-trisection
$\mathcal T$
is a boundary stabilisation of a pseudo-trisection
 $\mathcal T^*$
. Then
$\mathcal T^*$
. Then
 $\mathcal T'$
is an internal stabilisation of
$\mathcal T'$
is an internal stabilisation of
 $\mathcal T^*$
.
$\mathcal T^*$
.
Proof Item (1). This is an immediate consequence of the definition, by restricting the diagram to
![]() $(\Sigma _i', \boldsymbol {\delta }_i')$
and observing that it stabilizes to
$(\Sigma _i', \boldsymbol {\delta }_i')$
and observing that it stabilizes to
![]() $(\Sigma _i, \boldsymbol {\delta }_i).$
$(\Sigma _i, \boldsymbol {\delta }_i).$
Item (2). The complexity of the pseudo-trisection is unchanged since each
![]() $k_i$
is unchanged (as was observed in the proof of Lemma 4.12.) The complexity of the boundary decreases by 1, by Proposition 2.26.
$k_i$
is unchanged (as was observed in the proof of Lemma 4.12.) The complexity of the boundary decreases by 1, by Proposition 2.26.
Item (3). This is proved diagrammatically, in Figure 18. The top row shows local regions of a pseudo-trisection diagram of
![]() $\mathcal T^*$
, and
$\mathcal T^*$
, and
![]() $\alpha $
denotes the curve along which the boundary stabilisation occurs. Applying a boundary stabilisation along
$\alpha $
denotes the curve along which the boundary stabilisation occurs. Applying a boundary stabilisation along
![]() $\alpha $
followed by a boundary stabilisation shift, the resulting pseudo-trisection diagram is shown in the second row. Applying diffeomorphisms to the
$\alpha $
followed by a boundary stabilisation shift, the resulting pseudo-trisection diagram is shown in the second row. Applying diffeomorphisms to the
![]() $\Sigma _i'$
and
$\Sigma _i'$
and
![]() $\Sigma _C'$
, and isotoping the curves, the bottom row is obtained. Applying handleslides and isotopies to
$\Sigma _C'$
, and isotoping the curves, the bottom row is obtained. Applying handleslides and isotopies to
![]() $\mu $
, and a diffeomorphism rel boundary to
$\mu $
, and a diffeomorphism rel boundary to
![]() $\Sigma _C'$
, the diagram of the bottom row can be expressed as a type II torus stabilisation of the initial diagram. The result now follows from Proposition 4.8.
$\Sigma _C'$
, the diagram of the bottom row can be expressed as a type II torus stabilisation of the initial diagram. The result now follows from Proposition 4.8.
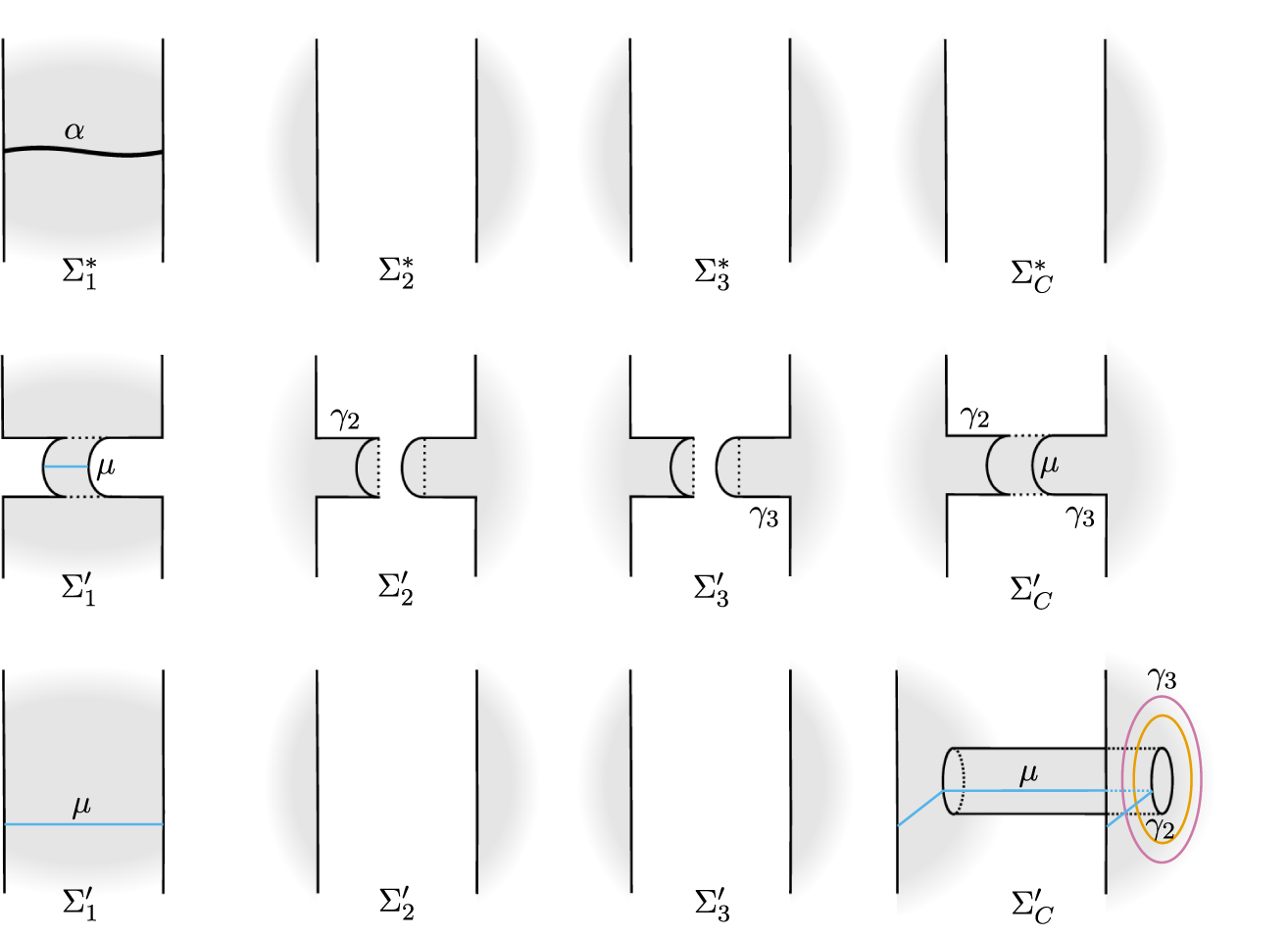
Figure 18: Proof of Proposition 4.13, item (3).
Theorem 1.1 Let X be a compact oriented 4-manifold with non-empty connected boundary Y. Let
![]() $\tau $
be a trisection of Y. Then there is a pseudo-trisection
$\tau $
be a trisection of Y. Then there is a pseudo-trisection
![]() $\mathcal T_1$
of X such that
$\mathcal T_1$
of X such that
![]() $\mathcal T_1 |_{Y} = \tau $
.
$\mathcal T_1 |_{Y} = \tau $
.
Proof Case 1:
![]() $\tau $
is the trivial trisection of
$\tau $
is the trivial trisection of
![]() $Y = S^3$
. Fill the boundary Y with a 4-ball
$Y = S^3$
. Fill the boundary Y with a 4-ball
![]() $B^4$
to obtain a closed manifold
$B^4$
to obtain a closed manifold
![]() $X\cup B^4$
. There is a trisection of
$X\cup B^4$
. There is a trisection of
![]() $X\cup B^4$
by the usual existence result in the closed setting [Reference Gay and Kirby7]. Choose any point in the central surface of the trisection, and there is a trivially trisected neighborhood N of the point. Now X is diffeomorphic to
$X\cup B^4$
by the usual existence result in the closed setting [Reference Gay and Kirby7]. Choose any point in the central surface of the trisection, and there is a trivially trisected neighborhood N of the point. Now X is diffeomorphic to
![]() $(X \cup B^4) - N$
, and the latter is equipped with a pseudo-trisection with boundary
$(X \cup B^4) - N$
, and the latter is equipped with a pseudo-trisection with boundary
![]() $\tau $
.
$\tau $
.
Case 2: Y is equipped with any trisection
![]() $\tau $
other than the trivial trisection of
$\tau $
other than the trivial trisection of
![]() $S^3$
. (Y may or may not be
$S^3$
. (Y may or may not be
![]() $S^3$
.) Equip X with a pseudo-trisection
$S^3$
.) Equip X with a pseudo-trisection
![]() $\mathcal T$
by Corollary 3.20. By Proposition 2.10, there is a trisection
$\mathcal T$
by Corollary 3.20. By Proposition 2.10, there is a trisection
![]() $\tau '$
of Y such that there is a sequence of stabilisations and Heegaard stabilisations from
$\tau '$
of Y such that there is a sequence of stabilisations and Heegaard stabilisations from
![]() $\mathcal T|_Y$
to
$\mathcal T|_Y$
to
![]() $\tau '$
, and a sequence of stabilisations from
$\tau '$
, and a sequence of stabilisations from
![]() $\tau $
to
$\tau $
to
![]() $\tau '$
. At the 4-dimensional level, there is an induced sequence of boundary stabilisations and Heegaard stabilisations from
$\tau '$
. At the 4-dimensional level, there is an induced sequence of boundary stabilisations and Heegaard stabilisations from
![]() $\mathcal T$
to some pseudo-trisection
$\mathcal T$
to some pseudo-trisection
![]() $\mathcal T'$
with
$\mathcal T'$
with
![]() $\mathcal T'|_Y = \tau '$
. Further, there is a sequence of boundary stabilisation shifts from
$\mathcal T'|_Y = \tau '$
. Further, there is a sequence of boundary stabilisation shifts from
![]() $\mathcal T'$
to a pseudo-trisection
$\mathcal T'$
to a pseudo-trisection
![]() $\mathcal T_1$
with
$\mathcal T_1$
with
![]() $\mathcal T_1|_Y = \tau $
.
$\mathcal T_1|_Y = \tau $
.
4.3 Orientations of pseudo-trisections
In this subsection, we outline a convention for how a pseudo-trisection diagram determines an orientation of the corresponding 4-manifold. In general, this requires one additional label to be added to the pseudo-trisection diagram.
-
(1) If the binding of the pseudo-trisection consists of one component and is depicted as a circle in the given pseudo-trisection diagram, it is oriented counterclockwise. Otherwise, one component of the binding must be labeled with an orientation.
-
(2) The orientation of the boundary component extends to an orientation of the surfaces
 $\Sigma _\circ , \circ \in \{C, 1, 2, 3\}$
by the outward-normal-first convention. (This further induces orientations on any remaining components of the binding.)
$\Sigma _\circ , \circ \in \{C, 1, 2, 3\}$
by the outward-normal-first convention. (This further induces orientations on any remaining components of the binding.) -
(3) An oriented normal vector to each
 $\Sigma _\circ $
is determined by the right hand rule. Pieces of the 3-skeleton are oriented as follows:
$\Sigma _\circ $
is determined by the right hand rule. Pieces of the 3-skeleton are oriented as follows:-
(a) The boundary
 $\partial Y_i$
of
$\partial Y_i$
of
 $Y_i$
is oriented as
$Y_i$
is oriented as
 $(-\Sigma _i) \cup \Sigma _{i+1}$
. Now
$(-\Sigma _i) \cup \Sigma _{i+1}$
. Now
 $Y_i$
is oriented by the outward-normal-first convention.
$Y_i$
is oriented by the outward-normal-first convention. -
(b) The boundary
 $\partial H_i$
of
$\partial H_i$
of
 $H_i$
is oriented as
$H_i$
is oriented as
 $(-\Sigma _C) \cup \Sigma _i$
. Now
$(-\Sigma _C) \cup \Sigma _i$
. Now
 $H_i$
is oriented by the outward-normal-first convention.
$H_i$
is oriented by the outward-normal-first convention.
-
-
(4) Next, the boundaries
 $\partial X_i$
of the sectors are oriented as
$\partial X_i$
of the sectors are oriented as
 $Y_i \cup H_i \cup (-H_{i+1})$
. The sectors
$Y_i \cup H_i \cup (-H_{i+1})$
. The sectors
 $X_i$
are oriented by the outward-normal-first convention.
$X_i$
are oriented by the outward-normal-first convention. -
(5) The 4-manifold X is oriented as
 $X_1 \cup X_2 \cup X_3$
. The boundary
$X_1 \cup X_2 \cup X_3$
. The boundary
 $\partial X = Y$
is oriented as
$\partial X = Y$
is oriented as
 $Y_1 \cup Y_2 \cup Y_3$
, and this orientation agrees with the induced boundary orientation from X.
$Y_1 \cup Y_2 \cup Y_3$
, and this orientation agrees with the induced boundary orientation from X.
5 Pseudo-bridge trisections
In this section, we extend from considering 4-manifolds to considering pairs
![]() $(X, \mathcal K)$
where
$(X, \mathcal K)$
where
![]() $\mathcal K$
is an embedded surface. In the case where X and
$\mathcal K$
is an embedded surface. In the case where X and
![]() $\mathcal K$
are closed, these pairs are understood via bridge trisections as in [Reference Meier and Zupan19]. In the relative case (i.e., when X is compact with boundary
$\mathcal K$
are closed, these pairs are understood via bridge trisections as in [Reference Meier and Zupan19]. In the relative case (i.e., when X is compact with boundary
![]() $\partial X$
, and
$\partial X$
, and
![]() $\mathcal K \subset X$
is a neatly embedded surface with boundary
$\mathcal K \subset X$
is a neatly embedded surface with boundary
![]() $L \subset \partial X$
), there is a notion of relative bridge trisections introduced in general in [Reference Meier17]. We summarize relative bridge trisections before introducing an analog of bridge position for pseudo-trisections. We also introduce pseudo-bridge trisection diagrams and describe how some properties of the encoded surface can be read off the diagrams. Recall the conventions for pairs
$L \subset \partial X$
), there is a notion of relative bridge trisections introduced in general in [Reference Meier17]. We summarize relative bridge trisections before introducing an analog of bridge position for pseudo-trisections. We also introduce pseudo-bridge trisection diagrams and describe how some properties of the encoded surface can be read off the diagrams. Recall the conventions for pairs
![]() $(X, \mathcal K)$
described in Section 1—the introduction.
$(X, \mathcal K)$
described in Section 1—the introduction.
5.1 Relative bridge trisections
The general theory of relative bridge trisections, due to Meier [Reference Meier17], is reviewed here.
In the same way that relative trisections are defined to be determined by the spine (equivalently, a diagram on the central surface), relative bridge trisections are defined so that the embedded surface is encoded by a diagram on the central surface (without, for example, having to describe the boundary link of the surface). This is achieved through additional Morse-theoretic structure.
Suppose X is equipped with a relative trisection. Let
![]() $N(B)$
be a tubular neighborhood of the binding of the relative trisection. Each
$N(B)$
be a tubular neighborhood of the binding of the relative trisection. Each
![]() $H_i' = (X_i \cap X_{i+1}) - N(B)$
has the structure of a compression body between two surfaces with boundary, namely
$H_i' = (X_i \cap X_{i+1}) - N(B)$
has the structure of a compression body between two surfaces with boundary, namely
![]() $\Sigma _C' = \Sigma _C - N(B)$
and
$\Sigma _C' = \Sigma _C - N(B)$
and
![]() $\Sigma _{i+1}' = \Sigma _{i+1} - N(B)$
. By virtue of being a compression body, there is a standard self-indexing Morse function
$\Sigma _{i+1}' = \Sigma _{i+1} - N(B)$
. By virtue of being a compression body, there is a standard self-indexing Morse function
![]() $\Phi _i$
which vanishes exactly on
$\Phi _i$
which vanishes exactly on
![]() $\Sigma _C'$
and is maximised exactly on
$\Sigma _C'$
and is maximised exactly on
![]() $\Sigma _{i+1}'$
. Let
$\Sigma _{i+1}'$
. Let
![]() $\tau _i$
be a tangle in
$\tau _i$
be a tangle in
![]() $H_i$
. It can be assumed that
$H_i$
. It can be assumed that
![]() $\tau _i$
lies in
$\tau _i$
lies in
![]() $H_i'$
because
$H_i'$
because
![]() $\tau _i$
avoids B by the transversality theorem. After an isotopy of
$\tau _i$
avoids B by the transversality theorem. After an isotopy of
![]() $\tau _i$
,
$\tau _i$
,
![]() $\Phi _i$
restricted to
$\Phi _i$
restricted to
![]() $\tau _i$
is Morse. An arc in
$\tau _i$
is Morse. An arc in
![]() $\tau _i$
is vertical if it has no local extrema, and is flat if it has a unique local extremum, which is a maximum.
$\tau _i$
is vertical if it has no local extrema, and is flat if it has a unique local extremum, which is a maximum.
Definition 5.1 Let
![]() $\tau _i$
be a tangle in
$\tau _i$
be a tangle in
![]() $H_i$
. This is a
$H_i$
. This is a
![]() $(b,v)$
-tangle if it is isotopic rel boundary to a tangle consisting exactly of b flat arcs and v vertical arcs. The v vertical arcs may end in separate components of
$(b,v)$
-tangle if it is isotopic rel boundary to a tangle consisting exactly of b flat arcs and v vertical arcs. The v vertical arcs may end in separate components of
![]() $\partial X$
, in which case the components are ordered and we have a
$\partial X$
, in which case the components are ordered and we have a
![]() $(b,\boldsymbol v)$
-tangle where
$(b,\boldsymbol v)$
-tangle where
![]() $\boldsymbol v$
is an ordered partition of v.
$\boldsymbol v$
is an ordered partition of v.
In relative trisections the compressionbodies
![]() $H_i$
are also handlebodies; the notion of triviality above ensures that all arcs can be simultaneously isotoped to lie in the boundary.
$H_i$
are also handlebodies; the notion of triviality above ensures that all arcs can be simultaneously isotoped to lie in the boundary.
Definition 5.2 Let
![]() $\mathcal {D}_i$
be a disk-tangle in
$\mathcal {D}_i$
be a disk-tangle in
![]() $X_i$
. This is a trivial tangle if it can be isotoped rel boundary to lie in
$X_i$
. This is a trivial tangle if it can be isotoped rel boundary to lie in
![]() $\partial X_i$
. In this case the boundary is an unlink in
$\partial X_i$
. In this case the boundary is an unlink in
![]() $H_i \cup H_{i-1}$
, and we say
$H_i \cup H_{i-1}$
, and we say
![]() $\partial \mathcal {D}_i$
is in
$\partial \mathcal {D}_i$
is in
![]() $(b,\boldsymbol v)$
-bridge position if the tangles in
$(b,\boldsymbol v)$
-bridge position if the tangles in
![]() $H_i$
and
$H_i$
and
![]() $H_{i-1}$
are both
$H_{i-1}$
are both
![]() $(b,\boldsymbol v)$
-tangles. Given that the boundary link of
$(b,\boldsymbol v)$
-tangles. Given that the boundary link of
![]() $\partial X_i$
is in
$\partial X_i$
is in
![]() $(b,\boldsymbol v)$
-bridge position, we say that
$(b,\boldsymbol v)$
-bridge position, we say that
![]() $\mathcal {D}_i$
is a
$\mathcal {D}_i$
is a
![]() $(c,\boldsymbol v)$
-disk-tangle, where
$(c,\boldsymbol v)$
-disk-tangle, where
![]() $c+v$
is the number of components of
$c+v$
is the number of components of
![]() $\mathcal {D}_i$
.
$\mathcal {D}_i$
.
Definition 5.3 Let X be a compact 4-manifold with boundary, and
![]() $\mathcal K$
a neatly embedded surface in X. Let
$\mathcal K$
a neatly embedded surface in X. Let
![]() $b,c, v$
be non-negative integers,
$b,c, v$
be non-negative integers,
![]() $\boldsymbol v$
an ordered partition of v into non-negative integers, and
$\boldsymbol v$
an ordered partition of v into non-negative integers, and
![]() $\boldsymbol c$
an ordered partition of c into three non-negative integers. The surface
$\boldsymbol c$
an ordered partition of c into three non-negative integers. The surface
![]() $\mathcal K$
is in
$\mathcal K$
is in
![]() $(b,\boldsymbol c; \boldsymbol v)$
-bridge trisected position in a relative trisection of X if
$(b,\boldsymbol c; \boldsymbol v)$
-bridge trisected position in a relative trisection of X if
-
(1) each
 $\mathcal D_i = X_i \cap \mathcal K$
is a trivial
$\mathcal D_i = X_i \cap \mathcal K$
is a trivial
 $(c_i; \boldsymbol v)$
-disk-tangle in
$(c_i; \boldsymbol v)$
-disk-tangle in
 $X_i$
, and
$X_i$
, and -
(2) each
 $\tau _i = H_i \cap \mathcal K$
is a
$\tau _i = H_i \cap \mathcal K$
is a
 $(b;\boldsymbol v)$
-tangle in
$(b;\boldsymbol v)$
-tangle in
 $H_i$
.
$H_i$
.
Remark 5.4 The above definition requires a lot of structure, keeping track of
![]() $(b,\boldsymbol c;\boldsymbol v)$
. This is essentially so that the
$(b,\boldsymbol c;\boldsymbol v)$
. This is essentially so that the
![]() $\tau _i$
are enough to encode the surface. In the case of pseudo-bridge trisections, we’ll introduce a more general notion of bridge position for which the analogs of
$\tau _i$
are enough to encode the surface. In the case of pseudo-bridge trisections, we’ll introduce a more general notion of bridge position for which the analogs of
![]() $\tau _i$
aren’t enough to encode the surface, but projections of tangles onto each surface in the pseudo-trisection diagram are enough. The overarching idea is that we’re generalizing the notion of bridge position in such a way as to obtain conceptually simpler diagrams and lower diagram complexity for a fixed surface (e.g., lower bridge index), but in exchange for diagrams with more pieces.
$\tau _i$
aren’t enough to encode the surface, but projections of tangles onto each surface in the pseudo-trisection diagram are enough. The overarching idea is that we’re generalizing the notion of bridge position in such a way as to obtain conceptually simpler diagrams and lower diagram complexity for a fixed surface (e.g., lower bridge index), but in exchange for diagrams with more pieces.
5.2 Pseudo-bridge trisections
Next we introduce pseudo-bridge trisections, the analog of relative bridge trisections in the setting of pseudo-trisections. We also introduce pseudo-shadow diagrams, which are analogous to shadow diagrams of relative bridge trisections. We show how a pseudo-shadow diagram uniquely encodes a pseudo-bridge trisection up to isotopy. We will immediately see that any pair
![]() $(X,\mathcal K)$
admits a pseudo-bridge trisection by application of the existence of relative bridge trisections.
$(X,\mathcal K)$
admits a pseudo-bridge trisection by application of the existence of relative bridge trisections.
Definition 5.5 Let X be a pseudo-trisected 4-manifold, and let
![]() $\mathcal K \subset X$
be a neatly embedded surface. The surface
$\mathcal K \subset X$
be a neatly embedded surface. The surface
![]() $\mathcal K$
is in pseudo-bridge position if
$\mathcal K$
is in pseudo-bridge position if
-
(1) each
 $\mathcal D_i = X_i \cap \mathcal K$
is a trivial disk-tangle in
$\mathcal D_i = X_i \cap \mathcal K$
is a trivial disk-tangle in
 $X_i$
, and
$X_i$
, and -
(2) each
 $\tau _i = H_i \cap \mathcal K$
and
$\tau _i = H_i \cap \mathcal K$
and
 $L_i = Y_i \cap \mathcal K$
is a trivial tangle in
$L_i = Y_i \cap \mathcal K$
is a trivial tangle in
 $H_i$
and
$H_i$
and
 $Y_i$
respectively.
$Y_i$
respectively.
Note that here a tangle is trivial if it can be isotoped rel boundary to lie in the boundary of the ambient space. A bridge point of the pseudo-bridge trisection is any point lying on the intersection between
![]() $\mathcal K$
and the 2-skeleton of the pseudo-trisection. The data of a pseudo-trisection together with a surface in pseudo-bridge position is termed a pseudo-bridge trisection.
$\mathcal K$
and the 2-skeleton of the pseudo-trisection. The data of a pseudo-trisection together with a surface in pseudo-bridge position is termed a pseudo-bridge trisection.
Example 5.6 The standard disk
![]() $D^2$
in
$D^2$
in
![]() $B^4$
admits a pseudo-bridge trisection which is also a relative bridge trisection. See Figure 19 (A).
$B^4$
admits a pseudo-bridge trisection which is also a relative bridge trisection. See Figure 19 (A).
-
(1) Let
 $B^4$
be the standard unit ball in
$B^4$
be the standard unit ball in
 $\mathbb {R}^4$
expressed in
$\mathbb {R}^4$
expressed in
 $\{r, \theta ,z,w\}$
-coordinates.
$\{r, \theta ,z,w\}$
-coordinates. -
(2) The trivial pseudo-trisection of
 $B^4$
3.12 (which is also a relative trisection) is given by decomposing into sectors with
$B^4$
3.12 (which is also a relative trisection) is given by decomposing into sectors with
 $0 \leq \theta \leq 2\pi /3$
,
$0 \leq \theta \leq 2\pi /3$
,
 $2\pi /3 \leq \theta \leq 4\pi /3$
, and
$2\pi /3 \leq \theta \leq 4\pi /3$
, and
 $4\pi /3 \leq \theta \leq 2\pi $
.
$4\pi /3 \leq \theta \leq 2\pi $
. -
(3) A standard disk embedding is given by
 $(z,w) = (0,0)$
. This disk intersects the aforementioned pseudo-trisection in bridge position.
$(z,w) = (0,0)$
. This disk intersects the aforementioned pseudo-trisection in bridge position.
One can show that this is a relative bridge trisection of the standard disk.

Figure 19: Schematics of two distinct pseudo-bridge trisections of a standard disk in
![]() $B^4$
.
$B^4$
.
Example 5.7 The standard disk in
![]() $B^4$
also admits a simpler pseudo-bridge trisection with less symmetry, which in particular is not a relative bridge trisection. See Figure 19 (B).
$B^4$
also admits a simpler pseudo-bridge trisection with less symmetry, which in particular is not a relative bridge trisection. See Figure 19 (B).
-
(1) Let
 $B^4$
be parametrized and trisected as in Example 5.6.
$B^4$
be parametrized and trisected as in Example 5.6. -
(2) Consider the cartesian parametrization of
 $\mathbb {R}^4$
, that is,
$\mathbb {R}^4$
, that is,
 $(x,y, z, w) = (r\cos \theta , r\sin \theta , z, w)$
. The plane
$(x,y, z, w) = (r\cos \theta , r\sin \theta , z, w)$
. The plane
 $(x,w) = (1/2, 0)$
intersects
$(x,w) = (1/2, 0)$
intersects
 $B^4$
along a standard disk as a pseudo-bridge trisection.
$B^4$
along a standard disk as a pseudo-bridge trisection.
This pseudo-trisection fails to be a relative trisection for Morse theoretic reasons: although
![]() $\tau _1$
is a trivial tangle, it has a local minimum and cannot be isopted to be flat or vertical.
$\tau _1$
is a trivial tangle, it has a local minimum and cannot be isopted to be flat or vertical.
Remark 5.8 Any
![]() $(X,\mathcal K)$
admits a pseudo-bridge trisection. First, there is a relative trisection
$(X,\mathcal K)$
admits a pseudo-bridge trisection. First, there is a relative trisection
![]() $\mathcal T$
of X with non-empty binding by the existence result of Gay and Kirby [Reference Gay and Kirby7]. Such a relative trisection is necessarily a pseudo-trisection by Proposition 3.18. On the other hand, by the existence result of Meier [Reference Meier17],
$\mathcal T$
of X with non-empty binding by the existence result of Gay and Kirby [Reference Gay and Kirby7]. Such a relative trisection is necessarily a pseudo-trisection by Proposition 3.18. On the other hand, by the existence result of Meier [Reference Meier17],
![]() $(X,\mathcal K)$
admits a relative bridge trisection whose underlying relative trisection is
$(X,\mathcal K)$
admits a relative bridge trisection whose underlying relative trisection is
![]() $\mathcal {T}$
. This relative bridge trisection is necessarily a pseudo-bridge trisection.
$\mathcal {T}$
. This relative bridge trisection is necessarily a pseudo-bridge trisection.
5.3 Pseudo-shadow diagrams
Shadow diagrams [Reference Meier17] are a diagrammatic theory of relative bridge trisections compatible with relative trisection diagrams. Here we introduce pseudo-shadow diagrams, a diagrammatic theory of pseudo-bridge trisections compatible with pseudo-trisection diagrams. In particular, any pair
![]() $(X,\mathcal K)$
admits a description by a pseudo-shadow diagram.
$(X,\mathcal K)$
admits a description by a pseudo-shadow diagram.
Definition 5.9 Let
![]() $\mathcal K, \mathcal K' \subset X$
. The surfaces
$\mathcal K, \mathcal K' \subset X$
. The surfaces
![]() $\mathcal K$
and
$\mathcal K$
and
![]() $\mathcal K'$
are neatly isotopic if they are homotopic through neat embeddings.
$\mathcal K'$
are neatly isotopic if they are homotopic through neat embeddings.
Proposition 5.10 A pseudo-bridge trisected surface
![]() $\mathcal K \subset X$
is determined up to neat isotopy by the 3-skeleton of the pseudo-bridge trisection, that is, by the data of all the tangles
$\mathcal K \subset X$
is determined up to neat isotopy by the 3-skeleton of the pseudo-bridge trisection, that is, by the data of all the tangles
![]() $(H_i, \tau _i)$
,
$(H_i, \tau _i)$
,
![]() $(Y_i, L_i)$
, and how they intersect.
$(Y_i, L_i)$
, and how they intersect.
Proof The data of the 3-skeleton describes how the triples
![]() $((H_i, \tau _i),(H_{i+1}, \tau _{i+1}),(Y_i, L_i))$
glue together to produce links in the boundaries of the sectors
$((H_i, \tau _i),(H_{i+1}, \tau _{i+1}),(Y_i, L_i))$
glue together to produce links in the boundaries of the sectors
![]() $X_i$
. These links are necessarily unlinks, which bound unique trivial disk-tangles in the sectors up to neat isotopy. Compare with [Reference Meier and Zupan19, Lemma 2.3 and Corollary 2.4].
$X_i$
. These links are necessarily unlinks, which bound unique trivial disk-tangles in the sectors up to neat isotopy. Compare with [Reference Meier and Zupan19, Lemma 2.3 and Corollary 2.4].
Consequently, we can define an analog of shadow diagrams as follows.
Definition 5.11 A pseudo-shadow diagram consists of the data
![]() $(\mathcal D, \tau _1, \tau _2, \tau _3, L_1,L_2,L_3)$
where
$(\mathcal D, \tau _1, \tau _2, \tau _3, L_1,L_2,L_3)$
where
-
(1)
 $\mathcal {D} = (\Sigma _C, \Sigma _i, \boldsymbol \alpha _i, \boldsymbol \delta _i)$
is a pseudo-trisection diagram.
$\mathcal {D} = (\Sigma _C, \Sigma _i, \boldsymbol \alpha _i, \boldsymbol \delta _i)$
is a pseudo-trisection diagram. -
(2) For
 $i \in \{1,2,3\}$
,
$i \in \{1,2,3\}$
,
 $\tau _i$
is a collection of generically embedded arcs in
$\tau _i$
is a collection of generically embedded arcs in
 $\Sigma _i \cup \Sigma _{C}$
, all with distinct endpoints. If any two arcs in a given
$\Sigma _i \cup \Sigma _{C}$
, all with distinct endpoints. If any two arcs in a given
 $\tau _i$
cross, the crossing order is indicated. The arcs intersect
$\tau _i$
cross, the crossing order is indicated. The arcs intersect
 $B = \partial \Sigma _i = \partial \Sigma _C$
transversely.
$B = \partial \Sigma _i = \partial \Sigma _C$
transversely. -
(3) Similarly, each
 $L_i$
is a collection of generically embedded arcs in
$L_i$
is a collection of generically embedded arcs in
 $\Sigma _i \cup \Sigma _{i+1}$
with distinct endpoints. If any two cross, the crossing order is indicated. Any intersections with B are transverse.
$\Sigma _i \cup \Sigma _{i+1}$
with distinct endpoints. If any two cross, the crossing order is indicated. Any intersections with B are transverse. -
(4) For any i,
 $\tau _i, L_i$
, and
$\tau _i, L_i$
, and
 $L_{i-1}$
may intersect
$L_{i-1}$
may intersect
 $\Sigma _i$
. Each of these families of arcs are pairwise transverse in
$\Sigma _i$
. Each of these families of arcs are pairwise transverse in
 $\Sigma _i$
.
$\Sigma _i$
. -
(5) There is a collection of points
 $\mathcal B_i \subset \Sigma _i$
which consists precisely of the endpoints of
$\mathcal B_i \subset \Sigma _i$
which consists precisely of the endpoints of
 $\tau _i, L_i$
, and
$\tau _i, L_i$
, and
 $L_{i-1}$
that lie in
$L_{i-1}$
that lie in
 $\Sigma _i$
. (Consequently, each point in
$\Sigma _i$
. (Consequently, each point in
 $\mathcal B_i$
has degree 3 in a pseudo-shadow diagram.)
$\mathcal B_i$
has degree 3 in a pseudo-shadow diagram.) -
(6) The above two points also hold verbatim for
 $(\Sigma _C, \tau _1, \tau _2, \tau _3)$
instead of
$(\Sigma _C, \tau _1, \tau _2, \tau _3)$
instead of
 $(\Sigma _i, \tau _i, L_i, L_{i-1})$
.The set of endpoints of arcs in
$(\Sigma _i, \tau _i, L_i, L_{i-1})$
.The set of endpoints of arcs in
 $\tau _i$
lying in
$\tau _i$
lying in
 $\Sigma _C$
is denoted
$\Sigma _C$
is denoted
 $\mathcal B_C$
.
$\mathcal B_C$
. -
(7) The unions
 $\tau _i \cup \tau _{i+1} \cup L_i$
form unlinks in each of the 3-dimensional manifolds encoded by the corresponding triple Heegaard diagram in the underlying pseudo-trisection diagram.
$\tau _i \cup \tau _{i+1} \cup L_i$
form unlinks in each of the 3-dimensional manifolds encoded by the corresponding triple Heegaard diagram in the underlying pseudo-trisection diagram.
For notational brevity, we frequently write
![]() $(\mathcal D, \tau _i, L_i)$
instead of
$(\mathcal D, \tau _i, L_i)$
instead of
![]() $(\mathcal D, \tau _1, \tau _2, \tau _3, L_1,L_2,L_3)$
.
$(\mathcal D, \tau _1, \tau _2, \tau _3, L_1,L_2,L_3)$
.
Definition 5.12 There is a realization map
 $$ \begin{align*}\mathcal R : \{\text{pseudo-shadow diagrams}\} \to \frac{\{\text{pseudo-bridge trisections}\}}{\text{diffeomorphism}}\end{align*} $$
$$ \begin{align*}\mathcal R : \{\text{pseudo-shadow diagrams}\} \to \frac{\{\text{pseudo-bridge trisections}\}}{\text{diffeomorphism}}\end{align*} $$
extending the realization map of Definition 4.2 defined as follows:
-
(1) A pseudo-shadow diagram has an underlying pseudo-trisection diagram. First, this is mapped to a pseudo-trisection by the realization map of Definition 4.2.
-
(2) Each collection of arcs
 $\tau _i$
and
$\tau _i$
and
 $L_i$
lies in the 2-skeleton of the above pseudo-trisection. Each collection is isotoped rel boundary to form a tangle in
$L_i$
lies in the 2-skeleton of the above pseudo-trisection. Each collection is isotoped rel boundary to form a tangle in
 $H_i$
and
$H_i$
and
 $Y_i$
, respectively.
$Y_i$
, respectively. -
(3) Each triple union
 $\tau _i \cup \tau _{i+1} \cup L_i$
forms an unlink in
$\tau _i \cup \tau _{i+1} \cup L_i$
forms an unlink in
 $\partial X_i$
. This bounds a collection of disks in
$\partial X_i$
. This bounds a collection of disks in
 $\partial X_i$
(uniquely up to isotopy rel boundary).
$\partial X_i$
(uniquely up to isotopy rel boundary). -
(4) The above collections of disks are isotoped rel boundary to be neatly embedded in
 $X_i$
. The result is now a pseudo-bridge trisection.
$X_i$
. The result is now a pseudo-bridge trisection.
Proposition 5.13 The realization map of Definition 5.12 is well defined.
Proof We must show that the map as defined truly sends a pseudo-shadow diagram to a pseudo-bridge trisection, and that any two pseudo-bridge trisections built from the same pseudo-shadow diagram by the map are neatly isotopic. (More precisely, after a diffeomorphism, the embedded surfaces differ by neat isotopy.)
Let
![]() $(X, \mathcal K)$
be the realization of a pseudo-shadow diagram
$(X, \mathcal K)$
be the realization of a pseudo-shadow diagram
![]() $\mathcal D$
. Then each
$\mathcal D$
. Then each
![]() $\mathcal K \cap X_i$
is necessarily a trivial disk tangle, because it is obtained by isotoping a collection of disks rel boundary from
$\mathcal K \cap X_i$
is necessarily a trivial disk tangle, because it is obtained by isotoping a collection of disks rel boundary from
![]() $\partial X_i$
to
$\partial X_i$
to
![]() $X_i$
. Similarly, each
$X_i$
. Similarly, each
![]() $\mathcal K \cap H_i$
and
$\mathcal K \cap H_i$
and
![]() $\mathcal K \cap Y_i$
is necessarily a trivial tangle. It follows that
$\mathcal K \cap Y_i$
is necessarily a trivial tangle. It follows that
![]() $(X, \mathcal K)$
is a pseudo-bridge trisection.
$(X, \mathcal K)$
is a pseudo-bridge trisection.
Next, suppose
![]() $(X, \mathcal K)$
and
$(X, \mathcal K)$
and
![]() $(X',\mathcal K')$
are realizations of the same pseudo-shadow diagram
$(X',\mathcal K')$
are realizations of the same pseudo-shadow diagram
![]() $\mathcal D$
. By Proposition 4.3, the underlying 4-manifolds X and
$\mathcal D$
. By Proposition 4.3, the underlying 4-manifolds X and
![]() $X'$
and their pseudo-trisections are diffeomorphic. Hereafter
$X'$
and their pseudo-trisections are diffeomorphic. Hereafter
![]() $\mathcal K, \mathcal K'$
are considered to both lie in X. The arcs
$\mathcal K, \mathcal K'$
are considered to both lie in X. The arcs
![]() $\tau _i$
and
$\tau _i$
and
![]() $L_i$
lift to the 2-skeleton of the pseudo-trisection of X, and are further isotoped into
$L_i$
lift to the 2-skeleton of the pseudo-trisection of X, and are further isotoped into
![]() $H_i$
and
$H_i$
and
![]() $Y_i$
respectively to produce exactly the 3-skeleta of
$Y_i$
respectively to produce exactly the 3-skeleta of
![]() $(X, \mathcal K)$
and
$(X, \mathcal K)$
and
![]() $(X, \mathcal K')$
. By Proposition 5.10, the 3-skeleta determine the surface in pseudo-bridge position up to neat isotopy.
$(X, \mathcal K')$
. By Proposition 5.10, the 3-skeleta determine the surface in pseudo-bridge position up to neat isotopy.
Example 5.14 Figure 20 is a pseudo-shadow diagram. This can be verified by inspecting the definition of a pseudo-shadow diagram. The most interesting condition is item (7). The union
![]() $\tau _1 \cup \tau _2 \cup L_1$
consists of an unknot in
$\tau _1 \cup \tau _2 \cup L_1$
consists of an unknot in
![]() $B^3$
, as shown in Figure 21.
$B^3$
, as shown in Figure 21.

Figure 20: A pseudo-shadow diagram of a disk in relative bridge position in
![]() $B^4$
.
$B^4$
.

Figure 21: The knot
![]() $\tau _1\cup \tau _2 \cup L_1 \subset S^3$
, see Example 5.14.
$\tau _1\cup \tau _2 \cup L_1 \subset S^3$
, see Example 5.14.
The underlying pseudo-trisection diagram of the aforementioned pseudo-shadow diagram is that of the trivial trisection (of
![]() $B^4$
). The surface is built by applying the realization map. Explicitly, the arcs
$B^4$
). The surface is built by applying the realization map. Explicitly, the arcs
![]() $\tau _1, \tau _2$
, and
$\tau _1, \tau _2$
, and
![]() $L_1$
lift to an unknot in
$L_1$
lift to an unknot in
![]() $\partial X_1 = B^3$
. Similarly,
$\partial X_1 = B^3$
. Similarly,
![]() $\tau _2, \tau _3, L_2$
lift to an unknot in
$\tau _2, \tau _3, L_2$
lift to an unknot in
![]() $\partial X_2 = B^3$
. The common intersection of these two unknots is
$\partial X_2 = B^3$
. The common intersection of these two unknots is
![]() $\tau _2$
. The two unknots next encode disks in
$\tau _2$
. The two unknots next encode disks in
![]() $X_1$
and
$X_1$
and
![]() $X_2$
respectively, and the union of these disks is itself a disk in
$X_2$
respectively, and the union of these disks is itself a disk in
![]() $X_1 \cup X_2$
with boundary
$X_1 \cup X_2$
with boundary
![]() $\tau _1 \cup \tau _3 \cup L_1 \cup L_2$
. Finally,
$\tau _1 \cup \tau _3 \cup L_1 \cup L_2$
. Finally,
![]() $\tau _1 \cup \tau _3 \cup L_3$
lifts to an unknot in
$\tau _1 \cup \tau _3 \cup L_3$
lifts to an unknot in
![]() $\partial X_3$
, which bounds a disk in
$\partial X_3$
, which bounds a disk in
![]() $X_3$
. Gluing in this final disk produces a disk in X exactly as in Figure 19 (A).
$X_3$
. Gluing in this final disk produces a disk in X exactly as in Figure 19 (A).
5.4 Resolving crossings in pseudo-shadow diagrams
When applying the realization map, arcs in the pseudo-shadow diagram are lifted from the 2-skeleton into the 3-skeleton. Crossings between arcs are resolved in different ways depending on the types of arcs, as well as whether or not the orientations of the underlying surface and 3-manifold are compatible. For example, in Section 4.3, we saw that
![]() $\partial Y_i = (-\Sigma _i) \cup \Sigma _{i+1}$
as an oriented union. Lifting a crossing from
$\partial Y_i = (-\Sigma _i) \cup \Sigma _{i+1}$
as an oriented union. Lifting a crossing from
![]() $\Sigma _i$
to
$\Sigma _i$
to
![]() $Y_i$
may reverse it, while lifting from
$Y_i$
may reverse it, while lifting from
![]() $\Sigma _{i+1}$
to
$\Sigma _{i+1}$
to
![]() $Y_i$
may preserve it. The following list outlines how to resolve any crossing when realizing a pseudo-bridge diagram.
$Y_i$
may preserve it. The following list outlines how to resolve any crossing when realizing a pseudo-bridge diagram.
Remark 5.16 The actual choice or convention happens when we declare how an orientation of the binding (of a pseudo-trisection diagram) induces an orientation of the pseudo-trisected 4-manifold. This determines exactly how arcs in a pseudo-shadow diagram must lift to the 4-manifold. The rules being outlined below should be thought of as “what do crossings between arcs in a pseudo-shadow diagram actually represent, given the orientation conventions from Section 4.3?”.
-
(1) For each i, consider the oriented pairs
 $(\partial X_i, \Sigma _i), (\partial X_i, \Sigma _{i+1}), (\partial X_i, \Sigma _C)$
, and
$(\partial X_i, \Sigma _i), (\partial X_i, \Sigma _{i+1}), (\partial X_i, \Sigma _C)$
, and
 $(Y, \Sigma _i)$
. Each of the twelve pairs is further equipped with a normal vector field on
$(Y, \Sigma _i)$
. Each of the twelve pairs is further equipped with a normal vector field on
 $\Sigma _{\circ }, \circ \in \{i, i+1, C\}$
which extends the orientation of
$\Sigma _{\circ }, \circ \in \{i, i+1, C\}$
which extends the orientation of
 $\Sigma _\circ $
to agree with the orientation of the ambient 3-manifold.
$\Sigma _\circ $
to agree with the orientation of the ambient 3-manifold. -
(2) In a pseudo-shadow diagram,
 $L_{i-1}$
lies above
$L_{i-1}$
lies above
 $L_{i}$
in the sense that any arcs of
$L_{i}$
in the sense that any arcs of
 $L_{i-1}$
intersecting arcs of
$L_{i-1}$
intersecting arcs of
 $L_{i}$
in
$L_{i}$
in
 $\Sigma _{i}$
lift to a position above
$\Sigma _{i}$
lift to a position above
 $L_{i}$
with respect to the aforementioned normal vector field on
$L_{i}$
with respect to the aforementioned normal vector field on
 $(Y, \Sigma _{i})$
. Similarly,
$(Y, \Sigma _{i})$
. Similarly,
 $\tau _i$
lies above
$\tau _i$
lies above
 $L_i$
;
$L_i$
;
 $L_i$
lies above
$L_i$
lies above
 $\tau _{i+1}$
; and
$\tau _{i+1}$
; and
 $\tau _{i+1}$
lies above
$\tau _{i+1}$
lies above
 $\tau _i$
. (Note that specifying two tangles in the pseudo-shadow diagram determines a unique ambient pair
$\tau _i$
. (Note that specifying two tangles in the pseudo-shadow diagram determines a unique ambient pair
 $(\partial X_i, \Sigma _i), \ldots , (Y, \Sigma _i)$
.)
$(\partial X_i, \Sigma _i), \ldots , (Y, \Sigma _i)$
.) -
(3) Any self-crossings, that is, crossings of
 $L_i$
or
$L_i$
or
 $\tau _i$
with themselves in
$\tau _i$
with themselves in
 $\Sigma _\circ $
, necessarily have crossing order indicated in the diagram. We say crossing orders are preserved if the over-strand lies above the under-strand and reversed otherwise. We have:
$\Sigma _\circ $
, necessarily have crossing order indicated in the diagram. We say crossing orders are preserved if the over-strand lies above the under-strand and reversed otherwise. We have:-
(a) Self-crossings of
 $L_{i}$
in
$L_{i}$
in
 $(Y, \Sigma _{i+1})$
and
$(Y, \Sigma _{i+1})$
and
 $(\partial X_{i}, \Sigma _{i+1})$
are preserved; self-crossings of
$(\partial X_{i}, \Sigma _{i+1})$
are preserved; self-crossings of
 $L_i$
in
$L_i$
in
 $(Y, \Sigma _i)$
and
$(Y, \Sigma _i)$
and
 $(\partial X_i, \Sigma _i)$
are reversed.
$(\partial X_i, \Sigma _i)$
are reversed. -
(b) Self-crossings of
 $\tau _i$
in
$\tau _i$
in
 $(\partial X_i, \Sigma _i)$
and
$(\partial X_i, \Sigma _i)$
and
 $(\partial X_{i-1}, \Sigma _C)$
are preserved; self-crossings of
$(\partial X_{i-1}, \Sigma _C)$
are preserved; self-crossings of
 $\tau _i$
in
$\tau _i$
in
 $(\partial X_i, \Sigma _C)$
and
$(\partial X_i, \Sigma _C)$
and
 $\partial X_{i-1}, \Sigma _i)$
are reversed.
$\partial X_{i-1}, \Sigma _i)$
are reversed.
-
Example 5.17 Figure 23 is a valid pseudo-shadow diagram of a neatly embedded surface
![]() $\mathcal K$
in
$\mathcal K$
in
![]() $B^4$
. The boundary link
$B^4$
. The boundary link
![]() $L_1 \cup L_2 \cup L_3 = \partial \mathcal K \subset S^3$
is easily seen to arise from a knot diagram with three crossings. However, determining whether it is an unknot, a left-handed trefoil, or right-handed trefoil requires some care.
$L_1 \cup L_2 \cup L_3 = \partial \mathcal K \subset S^3$
is easily seen to arise from a knot diagram with three crossings. However, determining whether it is an unknot, a left-handed trefoil, or right-handed trefoil requires some care.
We observe that the self-crossings are:
![]() $L_3$
in
$L_3$
in
![]() $\Sigma _1$
,
$\Sigma _1$
,
![]() $L_1$
in
$L_1$
in
![]() $\Sigma _2$
, and
$\Sigma _2$
, and
![]() $L_2$
in
$L_2$
in
![]() $\Sigma _3$
. It follows that each of the three self-crossings are preserved. Since every crossing is a negative crossing, it follows that the boundary knot is a left-handed trefoil.
$\Sigma _3$
. It follows that each of the three self-crossings are preserved. Since every crossing is a negative crossing, it follows that the boundary knot is a left-handed trefoil.

Figure 23: A pseudo-shadow diagram of a genus 1 surface in
![]() $B^4$
with boundary a trefoil knot. The boundary knot is given by
$B^4$
with boundary a trefoil knot. The boundary knot is given by
![]() $L_1, L_2,$
and
$L_1, L_2,$
and
![]() $L_3$
.
$L_3$
.
5.5 Pseudo-shadow diagram examples and calculations
In this subsection, we provide several examples of pseudo-shadow diagrams, and show how to compute some invariants such as orientability (of the embedded surface), the intrinsic topology of the surface, and the homology class represented by the surface in the ambient 4-manifold.
Proposition 5.18 A surface realizing a pseudo-shadow diagram is orientable if and only if the graph
![]() $\bigcup _i (L_i \cup \tau _i) \subset (\bigcup _i \Sigma _i) \cup \Sigma _C$
can be consistently labeled such that every vertex is either a source or a sink. (In this context the vertices are the bridge points and the intersections of the
$\bigcup _i (L_i \cup \tau _i) \subset (\bigcup _i \Sigma _i) \cup \Sigma _C$
can be consistently labeled such that every vertex is either a source or a sink. (In this context the vertices are the bridge points and the intersections of the
![]() $L_i$
and
$L_i$
and
![]() $\tau _i$
with the binding.)
$\tau _i$
with the binding.)
Proof This follows directly from the orientation convention of Section 4.3.
Example 5.19 Figure 24 is a pseudo-shadow diagram of a Möbius strip in
![]() $\mathbb {CP}^2 - B^4$
. To see that the surface represented by the diagram is non-orientable, observe that the vertices
$\mathbb {CP}^2 - B^4$
. To see that the surface represented by the diagram is non-orientable, observe that the vertices
![]() $b_1, b_2, b_3$
lie in a 3-cycle
$b_1, b_2, b_3$
lie in a 3-cycle
![]() $\gamma $
in the graph
$\gamma $
in the graph
![]() $\bigcup _i (L_i \cup \tau _i)$
, and therefore cannot be consistently labeled as sources or sinks. (For such a labeling to exist, any cycle must have even length.)
$\bigcup _i (L_i \cup \tau _i)$
, and therefore cannot be consistently labeled as sources or sinks. (For such a labeling to exist, any cycle must have even length.)

Figure 24: A pseudo-shadow diagram of a Möbius strip in pseudo-bridge position in
![]() $\mathbb {CP}^2 - B^4$
.
$\mathbb {CP}^2 - B^4$
.
Proposition 5.20 The Euler characteristic of a surface realizing a pseudo-shadow diagram
![]() $(\mathcal D, \tau _i, L_i)$
is given by
$(\mathcal D, \tau _i, L_i)$
is given by
![]() $F - |\mathcal {B}|/2$
, where F is the total number of components in each of the unlinks
$F - |\mathcal {B}|/2$
, where F is the total number of components in each of the unlinks
![]() $L_i \cup \tau _i \cup \tau _{i+1}$
in
$L_i \cup \tau _i \cup \tau _{i+1}$
in
![]() $\partial X_i$
, and
$\partial X_i$
, and
![]() $\mathcal B$
consists of all bridge points.
$\mathcal B$
consists of all bridge points.
Proof This follows from the usual formula of the Euler characteristic of a cellular complex. The number of 0-cells is
![]() $|\mathcal {B}|$
, and the number of 2-cells is F. Since bridge-points are 3-valent in a pseudo-shadow diagram, the number of 1-cells is
$|\mathcal {B}|$
, and the number of 2-cells is F. Since bridge-points are 3-valent in a pseudo-shadow diagram, the number of 1-cells is
![]() $3|\mathcal {B}|/2$
. The alternating sum of these quantities gives the desired result.
$3|\mathcal {B}|/2$
. The alternating sum of these quantities gives the desired result.
Example 5.21 Figure 25 is a valid pseudo-shadow diagram, and represents a surface in
![]() $\mathbb {CP}^2-B^4$
with boundary a left-handed trefoil in
$\mathbb {CP}^2-B^4$
with boundary a left-handed trefoil in
![]() $S^3$
. To see the trefoil, one can proceed as in Example 5.17. The links
$S^3$
. To see the trefoil, one can proceed as in Example 5.17. The links
![]() $L_i \cup \tau _i \cup \tau _{i+1}$
each have two components, so
$L_i \cup \tau _i \cup \tau _{i+1}$
each have two components, so
![]() $F=6$
in the Euler characteristic formula. On the other hand, there are 10 bridge points,
$F=6$
in the Euler characteristic formula. On the other hand, there are 10 bridge points,
![]() $\chi (\mathcal K) = 6 - 5 = 1$
. Since the surface has one boundary component, we know that it has genus
$\chi (\mathcal K) = 6 - 5 = 1$
. Since the surface has one boundary component, we know that it has genus
![]() $0$
. We conclude that the pseudo-shadow diagram represents a disk in
$0$
. We conclude that the pseudo-shadow diagram represents a disk in
![]() $\mathbb {CP}^2-B^4$
with boundary a trefoil. (Figuring out exactly which disk up to homology takes some more work.)
$\mathbb {CP}^2-B^4$
with boundary a trefoil. (Figuring out exactly which disk up to homology takes some more work.)

Figure 25: A slice disk of a left-handed trefoil in
![]() $\mathbb {CP}^2$
, representing
$\mathbb {CP}^2$
, representing
![]() $2[-\mathbb {CP}^1] \in H_2(\mathbb {CP}^2)$
.
$2[-\mathbb {CP}^1] \in H_2(\mathbb {CP}^2)$
.
Finally we describe how the homology class
![]() $[\mathcal K]$
in
$[\mathcal K]$
in
![]() $H_2(X)$
or
$H_2(X)$
or
![]() $H_2(X, \partial X)$
may be deduced from a pseudo-shadow diagram. The idea is to use Lefschetz duality to convert the problem into one of computing intersections of
$H_2(X, \partial X)$
may be deduced from a pseudo-shadow diagram. The idea is to use Lefschetz duality to convert the problem into one of computing intersections of
![]() $[\mathcal K]$
with other homology classes in
$[\mathcal K]$
with other homology classes in
![]() $H_2(X)$
or
$H_2(X)$
or
![]() $H_2(X, \partial X)$
. These intersections can then be computed diagrammatically.
$H_2(X, \partial X)$
. These intersections can then be computed diagrammatically.
The details are as follows. We first define the “intersection form”
by
![]() $(\alpha , \beta ) \mapsto \alpha ^*(\beta ))$
where
$(\alpha , \beta ) \mapsto \alpha ^*(\beta ))$
where
![]() $\alpha ^* \in H^2(X, \partial X)$
is the lift of
$\alpha ^* \in H^2(X, \partial X)$
is the lift of
![]() $\alpha $
to
$\alpha $
to
![]() $H^2(X, \partial X)$
via the cap product with the fundamental class, i.e.,
$H^2(X, \partial X)$
via the cap product with the fundamental class, i.e.,
Next we show that this intersection form is unimodular provided
![]() $H_1(X,\partial X)$
is torsion-free. By the universal coefficient theorem,
$H_1(X,\partial X)$
is torsion-free. By the universal coefficient theorem,
![]() $\operatorname {\mathrm {Hom}}(H_2(X, \partial X), \mathbb {Z})$
is isomorphic to
$\operatorname {\mathrm {Hom}}(H_2(X, \partial X), \mathbb {Z})$
is isomorphic to
![]() $H^2(X, \partial X)$
. Specifically, this is because
$H^2(X, \partial X)$
. Specifically, this is because
![]() $\text {Ext}^1(H_1(X, \partial X))$
vanishes when
$\text {Ext}^1(H_1(X, \partial X))$
vanishes when
![]() $H_1(X, \partial X)$
is torsion-free. Applying this isomorphism, the intersection form can be expressed as
$H_1(X, \partial X)$
is torsion-free. Applying this isomorphism, the intersection form can be expressed as
where the map is exactly that arising in Lefschetz duality. Therefore
![]() $Q_X'$
is invertible, and equivalently
$Q_X'$
is invertible, and equivalently
![]() $Q_X$
is unimodular.
$Q_X$
is unimodular.
When
![]() $Q_X$
is unimodular, we can use intersection data to deduce homology classes. Suppose
$Q_X$
is unimodular, we can use intersection data to deduce homology classes. Suppose
![]() $e_1,\ldots , e_n$
are generators of
$e_1,\ldots , e_n$
are generators of
![]() $H_2(X, \partial X)$
. Then knowing each of the
$H_2(X, \partial X)$
. Then knowing each of the
is enough to determine
![]() $[\mathcal K]$
. The final step is to express these intersections diagrammatically.
$[\mathcal K]$
. The final step is to express these intersections diagrammatically.
Suppose
![]() $\mathcal K, E_1, \ldots , E_n$
are surfaces in pseudo-bridge position in X. Then the intersections
$\mathcal K, E_1, \ldots , E_n$
are surfaces in pseudo-bridge position in X. Then the intersections
![]() $Q_X([\mathcal K], [E_j])$
are the sums of the intersections in each
$Q_X([\mathcal K], [E_j])$
are the sums of the intersections in each
![]() $X_i$
. In each
$X_i$
. In each
![]() $X_i$
, the intersections of disk tangles are equivalently the linking numbers of their boundaries. Therefore computing the intersections reduces to computing linking numbers of links in pseudo-shadow diagrams. This process is described in detail in the following example.
$X_i$
, the intersections of disk tangles are equivalently the linking numbers of their boundaries. Therefore computing the intersections reduces to computing linking numbers of links in pseudo-shadow diagrams. This process is described in detail in the following example.
Example 5.22 Figure 25 is a pseudo-shadow diagram of a disk
![]() $\mathcal K$
in
$\mathcal K$
in
![]() $\mathbb {CP}^2 - B^4$
with boundary a left-handed trefoil, introduced in Example 5.21. Next we determine the homology class
$\mathbb {CP}^2 - B^4$
with boundary a left-handed trefoil, introduced in Example 5.21. Next we determine the homology class
![]() $[\mathcal K] \in H_2(\mathbb {CP}^2 - B^4)$
via the procedure described above. We know that
$[\mathcal K] \in H_2(\mathbb {CP}^2 - B^4)$
via the procedure described above. We know that
![]() $H_2(\mathbb {CP}^2 - B^4) \cong H_2(\mathbb {CP}^2-B^4, S^3)$
is generated by
$H_2(\mathbb {CP}^2 - B^4) \cong H_2(\mathbb {CP}^2-B^4, S^3)$
is generated by
![]() $\mathbb {CP}^1$
, so our problem reduces to computing linking numbers of links in a pseudo-shadow diagram of
$\mathbb {CP}^1$
, so our problem reduces to computing linking numbers of links in a pseudo-shadow diagram of
![]() $\mathbb {CP}^1$
with those in Figure 25. We now describe, in detail, how to carry out this calculation in the sector
$\mathbb {CP}^1$
with those in Figure 25. We now describe, in detail, how to carry out this calculation in the sector
![]() $X_2$
. (The procedure is similar for sectors
$X_2$
. (The procedure is similar for sectors
![]() $X_1$
and
$X_1$
and
![]() $X_3$
.)
$X_3$
.)
-
(1) Figure 26 shows a pseudo-shadow diagram of
 $\mathbb {CP}^1$
. Restricting this diagram to
$\mathbb {CP}^1$
. Restricting this diagram to
 $(\Sigma _C, \Sigma _2, \Sigma _3, \alpha _2, \alpha _3, \tau _2', \tau _3')$
produces a triple Heegaard diagram of
$(\Sigma _C, \Sigma _2, \Sigma _3, \alpha _2, \alpha _3, \tau _2', \tau _3')$
produces a triple Heegaard diagram of
 $S^3$
, equipped with the data of
$S^3$
, equipped with the data of
 $\tau _2'$
and
$\tau _2'$
and
 $\tau _3'$
. Similarly, the pseudo-shadow diagram of Figure 25 can be restricted to a triple Heegaard diagram of
$\tau _3'$
. Similarly, the pseudo-shadow diagram of Figure 25 can be restricted to a triple Heegaard diagram of
 $S^3$
, equipped with the data of
$S^3$
, equipped with the data of
 $L_2, \tau _2$
, and
$L_2, \tau _2$
, and
 $\tau _3$
. The realization map lifts both
$\tau _3$
. The realization map lifts both
 $\gamma = L_2\cup \tau _2 \cup \tau _3$
and
$\gamma = L_2\cup \tau _2 \cup \tau _3$
and
 $\gamma ' = \tau _2' \cup \tau _3'$
to unlinks in
$\gamma ' = \tau _2' \cup \tau _3'$
to unlinks in
 $S^3$
. Our goal is to compute the linking number
$S^3$
. Our goal is to compute the linking number
 $lk(\gamma , \gamma ')$
. Figure 27 shows each of the aforementioned triple Heegaard diagrams overlayed as a single diagram. There is an apparent crossing, denoted x, between
$lk(\gamma , \gamma ')$
. Figure 27 shows each of the aforementioned triple Heegaard diagrams overlayed as a single diagram. There is an apparent crossing, denoted x, between
 $\gamma $
and
$\gamma $
and
 $\gamma '$
. Subsequent diagrammatic manipulations will determine how this crossing impacts
$\gamma '$
. Subsequent diagrammatic manipulations will determine how this crossing impacts
 $lk(\gamma , \gamma ')$
.
$lk(\gamma , \gamma ')$
.
Figure 26: A pseudo-shadow diagram of
 $\mathbb {CP}^1$
in
$\mathbb {CP}^1$
in
 $\mathbb {CP}^2 - B^4$
. Note that the surface has empty boundary. Referenced in Example 5.22.
$\mathbb {CP}^2 - B^4$
. Note that the surface has empty boundary. Referenced in Example 5.22.
Figure 27: Restrictions of pseudo-shadow diagrams for
 $\mathbb {CP}^1$
and a disk
$\mathbb {CP}^1$
and a disk
 $\mathcal K$
to
$\mathcal K$
to
 $X_2$
, referenced in Example 5.22. This is the first step in computing the intersection of
$X_2$
, referenced in Example 5.22. This is the first step in computing the intersection of
 $\mathbb {CP}^1$
and
$\mathbb {CP}^1$
and
 $\mathcal K$
(restricted to
$\mathcal K$
(restricted to
 $X_2$
).
$X_2$
). -
(2) To lift the curves
 $\gamma $
and
$\gamma $
and
 $\gamma '$
to
$\gamma '$
to
 $S^3$
, we must first build the underlying
$S^3$
, we must first build the underlying
 $S^3$
from the triple Heegaard diagram in Figure 27. To this end, we “cut and paste” the representation of
$S^3$
from the triple Heegaard diagram in Figure 27. To this end, we “cut and paste” the representation of
 $\Sigma _C$
so that the curves
$\Sigma _C$
so that the curves
 $\alpha _2$
and
$\alpha _2$
and
 $\alpha _3$
are standard axes on the torus. The result is depicted in Figure 28.
$\alpha _3$
are standard axes on the torus. The result is depicted in Figure 28. -
(3) Next, we glue the various pieces of the triple Heegaard diagram together. Figure 29 shows the result of identifying the “edges” of
 $\Sigma _C$
on the left, and the result of gluing each of
$\Sigma _C$
on the left, and the result of gluing each of
 $\Sigma _2, \Sigma _3$
, and
$\Sigma _2, \Sigma _3$
, and
 $\Sigma _C$
along their common boundary on the right. Note also that
$\Sigma _C$
along their common boundary on the right. Note also that
 $L_2$
has been lifted from
$L_2$
has been lifted from
 $\Sigma _2 \cup \Sigma _3$
to the sector
$\Sigma _2 \cup \Sigma _3$
to the sector
 $Y_2$
. This step is subtle: by the orientation convention,
$Y_2$
. This step is subtle: by the orientation convention,
 $\tau _2$
lies above
$\tau _2$
lies above
 $L_2$
, and
$L_2$
, and
 $L_2$
lies above
$L_2$
lies above
 $\tau _3$
. Indeed, they are depicted as such in the right hand diagram, and this is consistent with the orientations induced by the conventions of Section 4.3. Moreover, the convention requires that the self-crossing of
$\tau _3$
. Indeed, they are depicted as such in the right hand diagram, and this is consistent with the orientations induced by the conventions of Section 4.3. Moreover, the convention requires that the self-crossing of
 $L_2$
is reversed when lifting to
$L_2$
is reversed when lifting to
 $Y_2$
.
$Y_2$
.
Figure 29: Left: identifying the “edges” of
 $\Sigma _C$
. Right: the local structure of
$\Sigma _C$
. Right: the local structure of
 $\Sigma _2 \cup \Sigma _3 \cup \Sigma _C$
. Referenced in Example 5.22.
$\Sigma _2 \cup \Sigma _3 \cup \Sigma _C$
. Referenced in Example 5.22. -
(4) The arcs
 $\tau _2'$
lift to the sector of the trisection of
$\tau _2'$
lift to the sector of the trisection of
 $S^3$
lying “outside”
$S^3$
lying “outside”
 $\Sigma _C$
, and the arcs
$\Sigma _C$
, and the arcs
 $\tau _3'$
lift to the sector “inside”
$\tau _3'$
lift to the sector “inside”
 $\Sigma _C$
. The final result of lifting all arcs to the sectors
$\Sigma _C$
. The final result of lifting all arcs to the sectors
 $H_2, H_3, Y_2$
is shown in Figure 30. From here, it can be seen that
$H_2, H_3, Y_2$
is shown in Figure 30. From here, it can be seen that
 $lk(\gamma , \gamma ') = \pm 1$
, where
$lk(\gamma , \gamma ') = \pm 1$
, where
 $\gamma $
is an unlink with two components,
$\gamma $
is an unlink with two components,
 $\gamma _1$
and
$\gamma _1$
and
 $\gamma _2$
. The sign of the linking number depends on how the surface
$\gamma _2$
. The sign of the linking number depends on how the surface
 $\mathcal K$
is oriented.
$\mathcal K$
is oriented.
Figure 30: Lifting
 $\gamma $
and
$\gamma $
and
 $\gamma '$
to
$\gamma '$
to
 ${\mathbb {R}}^3 = S^3 - \{\text {pt}\}$
. Referenced in Example 5.22.
${\mathbb {R}}^3 = S^3 - \{\text {pt}\}$
. Referenced in Example 5.22.
In summary, we have established that
![]() $lk(\gamma , \gamma ') = lk(L_2\cup \tau _2\cup \tau _3, \tau _2'\cup \tau _3') = \pm 1$
. Further, this linking number is equal to the signed intersection of
$lk(\gamma , \gamma ') = lk(L_2\cup \tau _2\cup \tau _3, \tau _2'\cup \tau _3') = \pm 1$
. Further, this linking number is equal to the signed intersection of
![]() $\mathcal K \cap X_2$
with
$\mathcal K \cap X_2$
with
![]() $\mathbb {CP}^1 \cap X_2$
. Repeating this process in
$\mathbb {CP}^1 \cap X_2$
. Repeating this process in
![]() $X_1$
and
$X_1$
and
![]() $X_3$
, those linking numbers are found to be 0 and
$X_3$
, those linking numbers are found to be 0 and
![]() $\pm 1$
, respectively. Therefore
$\pm 1$
, respectively. Therefore
![]() $Q_{\mathbb {CP}^2}([\mathcal K], [\mathbb {CP}^1]) = 0 \pm 1 \pm 1 = \pm 2$
. Since
$Q_{\mathbb {CP}^2}([\mathcal K], [\mathbb {CP}^1]) = 0 \pm 1 \pm 1 = \pm 2$
. Since
![]() $Q_{\mathbb {CP}^2} = (1)$
, we deduce that
$Q_{\mathbb {CP}^2} = (1)$
, we deduce that
![]() $[\mathcal K] = 2H$
where
$[\mathcal K] = 2H$
where
![]() $H = \pm [\mathbb {CP}^1]$
is a generator of
$H = \pm [\mathbb {CP}^1]$
is a generator of
![]() $H_2(\mathbb {CP}^2)$
. This is consistent with the slice disk of a left handed trefoil in
$H_2(\mathbb {CP}^2)$
. This is consistent with the slice disk of a left handed trefoil in
![]() $\mathbb {CP}^2$
described in [Reference Manolescu, Marengon and Piccirillo16, Example 2.4]. Fixing an orientation of the left handed trefoil would fix the sign of
$\mathbb {CP}^2$
described in [Reference Manolescu, Marengon and Piccirillo16, Example 2.4]. Fixing an orientation of the left handed trefoil would fix the sign of
![]() $[\mathcal K]$
.
$[\mathcal K]$
.
Acknowledgements
The author is deeply grateful to Ciprian Manolescu for his continued support across many meetings, and Maggie Miller for many helpful conversations. The author sincerely thanks the anonymous referees for their insightful comments which improved this work. Further, the author thanks Sarah Blackwell, Cole Hugelmeyer, Gabriel Islambouli, and Peter Lambert-Cole for helpful discussions.









































































