Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-23T00:16:17.900Z Has data issue: false hasContentIssue false
  • English
  • Français

Pseudolocality for the Ricci Flow and Applications

Published online by Cambridge University Press:  20 November 2018

Albert Chau ,
Luen-Fai Tam  and
Chengjie Yu
Albert Chau
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC email: [email protected]
Luen-Fai Tam
Affiliation:
Department of Mathematics, The Chinese University of Hong Kong, Shatin, Hong Kong, China email: [email protected]
Chengjie Yu
Affiliation:
Department of Mathematics, Shantou University, Shantou Guangdong, China email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

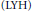Perelman established a differential Li-Yau-Hamilton $\left( \text{LHY} \right)$ type inequality for fundamental solutions of the conjugate heat equation corresponding to the Ricci flow on compact manifolds. As an application of the 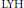$\text{LHY}$ inequality, Perelman proved a pseudolocality result for the Ricci flow on compact manifolds. In this article we provide the details for the proofs of these results in the case of a complete noncompact Riemannian manifold. Using these results we prove that under certain conditions, a finite time singularity of the Ricci flow must form within a compact set. The conditions are satisfied by asymptotically flatmanifolds. We also prove a long time existence result for the Kähler-Ricci flow on complete nonnegatively curved Kähler manifolds.

Keywords

53C4458J3735B35
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 1 , 01 February 2011 , pp. 55 - 85
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Chau, A. and Tam, L.-F., On the complex structure of Kahler manifolds with non-negative curvature. J. Differential Geom. 73(2006), no. 3, 491-530.Google Scholar
[2] Chau, A. and Tam, L.-F., Non-negatively curved Kähler manifolds with average quadratic curvature decay. Comm. Anal. Geom. 15(2007), no. 1, 121-146.Google Scholar
[3] Cheeger, J., Gromov, M., and Taylor, M., Finite propagation speed, kernel estimate for functions of the Laplace operator, and the geometry of complete Riemannian manifolds. J. Differential Geom. 17(1982), no. 1, 15-53.Google Scholar
[4] Chen, B.-L. and Zhu, X.-P., Volume growth and curvature decay of positively Curved Kähler manifolds. Q. J. Pure Appl. Math. 1(2005), no. 1, 68-108.Google Scholar
[5] Chen, B.-L. and Zhu, X.-P., Uniqueness of the Ricci flow on complete noncompact manifolds. J. Differential Geom. 74(2006), no. 1, 119-154.Google Scholar
[6] Chow, B. and Knopf, D., The Ricci flow: an introduction. Mathematical Surveys and Monographs, 110, American Mathematical Society, Providence, RI, 2004.Google Scholar
[7] Chow, B., Lu, P., and Ni, L., Hamilton's Ricci flow. Graduate Studies in Mathematics, 77, American Mathematical Society, Providence, RI; Science Press, New York, 2006.Google Scholar
[8] Davies, E. B., Heat kernels and spectral theory. Cambridge Tracts in Mathematics, 92, Cambridge University Press, Cambridge, 1989.Google Scholar
[9] Ecker, K. and Huisken, G., Interior estimates for hypersurfaces moving by mean curvature. Invent. Math. 105(1991), no. 3, 547-569. doi:10.1007/BF01232278Google Scholar
[10] Grigor'yan, A., Gaussian upper bounds for the heat kernel on arbitrary manifolds. J. Differential Geom. 45(1997), no. 1, 33-52.Google Scholar
[11] Guenther, C. M., The fundamental solution on manifolds with time-dependent metrics. J. Geom. Anal. 12(2002), no. 3, 425-436.Google Scholar
[12] Hamilton, R. S., A compactness property for solutions of the Ricci flow. Amer. J. Math. 117(1995), no. 3, 545-572. doi:10.2307/2375080Google Scholar
[13] Hamilton, R. S., The formation of singularities in the Ricci flow. In: Surveys in differential geometry, II, Int. Press, Cambridge, MA, 1995, pp. 7-136.Google Scholar
[14] Kleiner, B. and Lott, J., Notes on Perelman's papers. Geom. Topol. 12(2008), no. 5, 2587-2855. doi:10.2140/gt.2008.12.2587Google Scholar
[15] Kuang, S. and Zhang, Q. S., A gradient estimate for all positive solutions of the conjugate heat equation under Ricci flow. J. Funct. Anal. 255(2008), no. 4, 1008-1023. doi:10.1016/j.jfa.2008.05.014Google Scholar
[16] Li, P. and Schoen, R., Lp and mean value properties of subharmonic functions on Riemannian manifolds. Acta Math. 153(1984), no. 3-4, 279-301. doi:10.1007/BF02392380Google Scholar
[17] Li, P. and Yau, S.-T., On the parabolic kernel of the Schrödinger operator. Acta Math. 156(1986), no. 3-4, 153-201. doi:10.1007/BF02399203Google Scholar
[18] Ni, L., The entropy formula for linear heat equation. J. Geom. Anal. 14(2004), no. 1, 87-100.Google Scholar
[19] Ni, L., Ricci flow and nonnegativity of sectional curvature. Math. Res. Lett. 11(2004), no. 5-6, 883-904.Google Scholar
[20] Ni, L., Ancient solutions to Kähler-Ricci flow. Math. Res. Lett. 12(2005), no. 5-6, 633-653.Google Scholar
[21] Ni, L., A note on Perelman's LYH inequality. Comm. Anal. Geom. 14(2006), no. 5, 883-905.Google Scholar
[22] Ni, L. and Tam, L.-F., Plurisubharmonic functions and the structure of complete Kähler manifolds with nonnegative curvature. J. Differential Geom. 64(2003), no. 3, 457-524.Google Scholar
[23] Ni, L. and Tam, L.-F., Kähler-Ricci flow and the Poincaré-Lelong equation. Comm. Anal. Geom. 12(2004), no. 1-2, 111-141.Google Scholar
[24] Perelman, G., The entropy formula for the Ricci flow and its geometric applications. arXiv:math.DG/0211159.Google Scholar
[25] Saloff-Coste, L., Uniformly elliptic operators on Riemannian manifolds. J. Differential Geom. 36(1992), no. 2, 417-450.Google Scholar
[26] Shi, W.-X., Deformation the metric on complete Riemannian manifolds. J. Differential Geom. 30(1989), no. 1, 223-301.Google Scholar
[27] Shi, W.-X., Ricci flow and the uniformization on complete noncompact Kähler manifolds. J. Differential Geom. 45(1997), no. 1, 94-220.Google Scholar
[28] Tam, L.-F., Exhaustion function on complete manifolds. In: Recent advances in geometric analysis, Adv. Lect. Math., 11, Int. Press, Somerville, MA, 2010, pp. 211-215.Google Scholar
[29] Zhang, Q. S., Some gradient estimates for the heat equation on domains and for an equation by Perelman. Int. Math. Res. Not. 2006, Art. ID 92314, 39 pp.Google Scholar