Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T17:43:20.424Z Has data issue: false hasContentIssue false
  • English
  • Français

p–adic Families of Cohomological Modular Forms for Indefinite Quaternion Algebras and the Jacquet–LanglandsCorrespondence

Published online by Cambridge University Press:  20 November 2018

Matthew Greenberg  and
Marco Seveso
Matthew Greenberg
Affiliation:
Department of Mathematics and Statistics, University of Calgary, Calgary, AB T2N 1N4 e-mail: [email protected]
Marco Seveso
Affiliation:
Dipartimento di Matematica, Universitá di Milano, 20133 Milano, Italia e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We use the method of Ash and Stevens to prove the existence of small slope 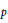$p$-adic families of cohomological modular forms for an indefinite quaternion algebra 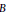$B$. We prove that the Jacquet–Langlands correspondence relating modular forms on 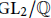$\text{G}{{\text{L}}_{\text{2}}}/\mathbb{Q}$ and cohomomological modular forms for 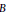$B$ is compatible with the formation of 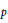$p$-adic families. This result is an analogue of a theorem of Chenevier concerning definite quaternion algebras.

Keywords

11F1111F6711F85modular formsp–adic familiesJacquet–Langlands correspondenceShimura curveseigencurves
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 5 , 01 October 2016 , pp. 961 - 998
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Andreatta, F., Iovita, A., and Pilloni, V., p-adic families of Siegel modular cuspforms. Ann. of Math. 181(2015), no. 2, 623–697. http://dx.doi.Org/10.4007/annals.2015.181.2.5 Google Scholar
[2] Andreatta, F., Iovita, A., and Stevens, G., Overconvergent modular sheaves and modular forms. Israel J. Math. 201(2014), no. 1, 299–359. http://dx.doi.org/10.1007/s11856-014-1045-8 Google Scholar
[3] Ash, A. and Stevens, G., sdecompositions.Preprint, available at http://math.bu.edu/people/ghs/research.html Google Scholar
[4] Ash, A., p-adic deformation of arithmetic cohomology.Preprint, available at http://math.bu.edu/people/ghs/research.html Google Scholar
[5] S.|Bosch, U.|Guntzer, and R. |Remmert, Non-archimedean analysis. Grundlehren der Mathematischen Wissenschaften, 261, Springer-Verlag, Berlin, 1984. http://dx.doi.org/10.1007/978-3-642-52229-1 Google Scholar
[6] Chenevier, G., Une correspondance de Jaquet-Langlands p-adique. Duke Math. Journal 126(2005),161–194. http://dx.doi.org/10.1215/S0012-7094-04-12615-6 Google Scholar
[7] Coleman, R., p-adic Banach spaces and families of modular forms. Invent. Math. 127(1997), no. 3, 417–479. http://dx.doi.org/10.1OO7/sOO222OO5O127 Google Scholar
[8] Darmon, H., Integration of Jp x J and arithmetic applications. Ann. of Math. 154(2001), no. 3, 589–639. http://dx.doi.org/10.2307/3062142 Google Scholar
[9] Dasgupta, S. and Greenberg, M., L-invariants and Shimura curves. Algebra and Number Theory 6(2012), no. 3, 455–485. http://dx.doi.Org/10.2140/ant.2012.6.455 Google Scholar
[10] Emerton, M., p-adic L-functions and unitary completions of representations of p-adic reductive groups. Duke Math. J. 130(2005), no. 2, 353–392.Google Scholar
[11] Emerton, M., On the interpolation of systems of eigenvalues attached to automorphic Hecke eigenforms. Invent. Math. 164(2006), no. 1, 1–84. http://dx.doi.org/10.1007/s00222-005-0448-x Google Scholar
[12] M.|Greenberg, Stark-Heegner points and the cohomology of quaternionic Shimura varieties. Duke Math. J. 147(2009), no. 3, 541–575.http://dx.doi.org/10.1215/00127094-2009-017 Google Scholar
[13] Greenberg, M., Seveso, M. A., and Shahabi, S., Modular p-adic L-functions attached to real quadratic fields and arithmetic applications. J. Reine Angew. Math., to appear. http://dx.doi.Org/10.1 515/crelle-2O1 4-0088 Google Scholar
[14] Newton, J. Completed cohomology of Shimura curves and a p-adic Jacquet-Langlands correspondence. Math. Ann. 355(2013), no. 2, 729–763. http://dx.doi.Org/10.1007/s00208-012-0796-y Google Scholar
[15] Rotger, V. and Seveso, M. A., L-invariants and Darmon cycles attached to modular forms. J. Eur.Math. Soc. 14(2012), no. 6, 1955–1999. http://dx.doi.org/10.41 71/JEMS/352 Google Scholar
[16] Schneider, P., Nonarchimedean functional analysis. Springer Monographs in Mathematics,Springer-Verlag, Berlin, 2002. http://dx.doi.org/10.1007/978-3-662-04728-6 Google Scholar
[17] Schneider, P. and Teitelbaum, J., Locally analytic distributions and p-adic representation theory,with applications to GL2. J. Amer. Math. Soc. 15(2002), no. 2, 443–468. http://dx.doi.Org/10.1090/S0894-0347-01-00377-0 Google Scholar
[18] Serre, J.-P., Endomorphismes complètement continus des espace de Banach p-adiques. Inst. Hautes Études Sci. Publ. Math. 12(1962), 69–85.Google Scholar
[19] Seveso, M. A., p-adic L-functions and the rationality of Darmon cycles. Canad. J. Math. 64(2012), no. 5, 1122–1181. http://dx.doi.org/10.4153/CJM-2011-076-8 Google Scholar
[20] Seveso, M. A., The Teitelbaum conjecture in the indefinite setting. Amer. J. Math. 135(2013), no. 6, 1525–1557. http://dx.doi.org/10.1353/ajm.2013.0055M Google Scholar
[21] Shimura, G., Introduction to the arithmetic theory of automorphic functions. Publications of the Mathematical Society of Japan, 11, Iwanami Shoten, Publishers, Tokyo; Princeton University Press, Princeton, NJ, 1971.Google Scholar
[22] Stevens, G., Rigid analytic modular symbols. Preprint, available at http://math.bu.edu/people/ghs/research.html Google Scholar