Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-06T10:42:54.177Z Has data issue: false hasContentIssue false
  • English
  • Français

A Packing Problem for Measurable Sets

Published online by Cambridge University Press:  20 November 2018

D. Sankoff  and
D. A. Dawson
D. Sankoff
Affiliation:
Department of Mathematics, McGill University, Montreal, Quebec
D. A. Dawson
Affiliation:
Department of Mathematics, McGill University, Montreal, Quebec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a probability measure space (Ω, 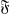, P) consider the following packing problem. What is the maximum number, b(K, Λ), of sets which may be chosen from 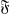so that each set has measure K and no two sets have intersection of measure larger than Λ < K?

In this paper the packing problem is solved for any non-atomic probability measure space. Rather than obtaining the solution explicitly, however, it is convenient to solve the following minimal paving problem. In a non-atomic a-finite measure space (Ω, 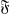, μ) what is the measure, V(b, K, Λ), of the smallest set which is the union of exactly b subsets of measure K such that no subsets have intersection of measure larger than Λ?

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 19 , 1967 , pp. 749 - 756
Copyright
Copyright © Canadian Mathematical Society 1967

References

1. Dantzig, G. B., “Formulating and solving linear programs,” Modern mathematics for the engineer, vol. 2 (New York, 1961).Google Scholar
2. Lorentz, G. G., Metric entropy and approximation, Bull. Amer. Math. Soc., 72 (1966), 903–937.Google Scholar
3. Ryser, H. J., Combinatorial mathematics, Carus Mathematical Monograph No. 14 (1963).Google Scholar
4. Spitzer, F., Principles of random walk (Princeton, 1964).Google Scholar