Article contents
On the Steinberg Map and Steinberg Cross-Section for a Symmetrizable Indefinite Kac-Moody Group
Published online by Cambridge University Press: 20 November 2018
Abstract
Let  $G$ be a symmetrizable indefinite Kac-Moody group over
$G$ be a symmetrizable indefinite Kac-Moody group over 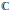 $\mathbb{C}$. Let
$\mathbb{C}$. Let 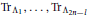 $\text{T}{{\text{r}}_{{{\Lambda }_{1}}\,,\ldots ,\,}}\text{T}{{\text{r}}_{{{\Lambda }_{2n-l}}}}$ be the characters of the fundamental irreducible representations of
$\text{T}{{\text{r}}_{{{\Lambda }_{1}}\,,\ldots ,\,}}\text{T}{{\text{r}}_{{{\Lambda }_{2n-l}}}}$ be the characters of the fundamental irreducible representations of  $G$, defined as convergent series on a certain part
$G$, defined as convergent series on a certain part 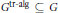 ${{G}^{\text{tr}-\text{alg}}}\,\subseteq \,G$. Following Steinberg in the classical case and Brüchert in the affine case, we define the Steinberg map
${{G}^{\text{tr}-\text{alg}}}\,\subseteq \,G$. Following Steinberg in the classical case and Brüchert in the affine case, we define the Steinberg map 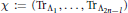 $\chi \,:=\,\left( \text{T}{{\text{r}}_{{{\Lambda }_{1}},\ldots ,}}\text{T}{{\text{r}}_{{{\Lambda }_{2n-l}}}} \right)$ as well as the Steinberg cross section
$\chi \,:=\,\left( \text{T}{{\text{r}}_{{{\Lambda }_{1}},\ldots ,}}\text{T}{{\text{r}}_{{{\Lambda }_{2n-l}}}} \right)$ as well as the Steinberg cross section 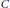 $C$, together with a natural parametrisation
$C$, together with a natural parametrisation 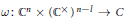 $\omega :{{\mathbb{C}}^{n}}\times {{\left( {{\mathbb{C}}^{\times }} \right)}^{n-l}}\to C$. We investigate the local behaviour of
$\omega :{{\mathbb{C}}^{n}}\times {{\left( {{\mathbb{C}}^{\times }} \right)}^{n-l}}\to C$. We investigate the local behaviour of  $\text{ }\!\!\chi\!\!\text{ }$ on
$\text{ }\!\!\chi\!\!\text{ }$ on 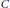 $C$ near
$C$ near 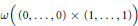 $\omega \left( \,\left( 0,\ldots 0 \right)\,\times \,\left( 1,\ldots ,1 \right)\, \right)$, and we show that there exists a neighborhood of
$\omega \left( \,\left( 0,\ldots 0 \right)\,\times \,\left( 1,\ldots ,1 \right)\, \right)$, and we show that there exists a neighborhood of 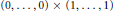 $\left( 0,...,0 \right)\,\,\times \,\,\left( 1,...,1 \right)$, on which
$\left( 0,...,0 \right)\,\,\times \,\,\left( 1,...,1 \right)$, on which 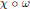 $\text{ }\!\!\chi\!\!\text{ }\,\circ \,\omega $ is a regular analytical map, satisfying a certain functional identity. This identity has its origin in an action of the center of
$\text{ }\!\!\chi\!\!\text{ }\,\circ \,\omega $ is a regular analytical map, satisfying a certain functional identity. This identity has its origin in an action of the center of  $G$ on
$G$ on 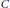 $C$.
$C$.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2001
References
- 1
- Cited by


