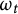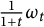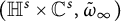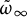1 Introduction
Oeljeklaus–Toma manifolds are a very interesting class of complex manifolds introduced and first studied in [Reference Oeljeklaus and Toma17]. These manifolds are defined as compact quotients of the type
where
![]() $\mathbb {H}\subseteq {\mathbb C}$
is the upper half-plane,
$\mathbb {H}\subseteq {\mathbb C}$
is the upper half-plane,
![]() $\mathcal O_{\mathbb {K}}$
is the ring of algebraic integers of an algebraic extension
$\mathcal O_{\mathbb {K}}$
is the ring of algebraic integers of an algebraic extension
![]() $\mathbb K$
of
$\mathbb K$
of
![]() $\mathbb Q$
satisfying
$\mathbb Q$
satisfying
![]() $[\mathbb K : \mathbb Q]=r+2s$
, and U is a free subgroup of rank r of
$[\mathbb K : \mathbb Q]=r+2s$
, and U is a free subgroup of rank r of
![]() $\mathcal O^{*,+}_{\mathbb {K}}$
satisfying some compatible conditions. The action of
$\mathcal O^{*,+}_{\mathbb {K}}$
satisfying some compatible conditions. The action of
![]() $U \ltimes \mathcal O_{\mathbb {K}}$
on
$U \ltimes \mathcal O_{\mathbb {K}}$
on
![]() $\mathbb H^r\times \mathbb C^s$
is defined via some embeddings of
$\mathbb H^r\times \mathbb C^s$
is defined via some embeddings of
![]() $\mathbb K$
in
$\mathbb K$
in
![]() $\mathbb R$
and
$\mathbb R$
and
![]() $\mathbb C$
. Oeljeklaus–Toma manifolds have a rich geometric structure. For instance, they have a natural structure of
$\mathbb C$
. Oeljeklaus–Toma manifolds have a rich geometric structure. For instance, they have a natural structure of
![]() $\mathbb T^{r+2s}$
-torus bundle over a
$\mathbb T^{r+2s}$
-torus bundle over a
![]() $\mathbb T^r$
and a structure of solvmanifold [Reference Kasuya13], i.e., they are always compact quotients of a solvable Lie group by a lattice. The Poincaré metricFootnote
1
$\mathbb T^r$
and a structure of solvmanifold [Reference Kasuya13], i.e., they are always compact quotients of a solvable Lie group by a lattice. The Poincaré metricFootnote
1
![]() $\omega _{\mathbb H^r}=\sqrt {-1}\sum _{a=1}^r\frac {dz_a\wedge d\bar z_a}{4(\Im \mathfrak m z_a)^2}$
induces a degenerate metric
$\omega _{\mathbb H^r}=\sqrt {-1}\sum _{a=1}^r\frac {dz_a\wedge d\bar z_a}{4(\Im \mathfrak m z_a)^2}$
induces a degenerate metric
![]() $\omega _\infty $
on M which has a central role in the study of geometric flows on these manifolds. The pair
$\omega _\infty $
on M which has a central role in the study of geometric flows on these manifolds. The pair
![]() $(r,s)$
is called the type of the manifold. The case of type
$(r,s)$
is called the type of the manifold. The case of type
![]() $(r,s)=(1,1)$
corresponds to the Inoue–Bombieri surfaces [Reference Inoue11].
$(r,s)=(1,1)$
corresponds to the Inoue–Bombieri surfaces [Reference Inoue11].
In [Reference Angella and Tosatti2, Reference Fang, Tosatti, Weinkove and Zheng7, Reference Tosatti and Weinkove28, Reference Zheng32], the Chern–Ricci flow [Reference Gill10, Reference Tosatti and Weinkove29] on Oeljeklaus–Toma manifolds M of type
![]() $(r,1)$
is studied. According to the results in [Reference Angella and Tosatti2, Reference Fang, Tosatti, Weinkove and Zheng7, Reference Tosatti and Weinkove28, Reference Zheng32], under some assumptions on the initial Hermitian metric, the flow has a long-time solution
$(r,1)$
is studied. According to the results in [Reference Angella and Tosatti2, Reference Fang, Tosatti, Weinkove and Zheng7, Reference Tosatti and Weinkove28, Reference Zheng32], under some assumptions on the initial Hermitian metric, the flow has a long-time solution
![]() $\omega _t$
such that
$\omega _t$
such that
![]() $(M,\frac {\omega _t}{1+t})$
converges in the Gromov–Hausdorff sense to an r-dimensional torus
$(M,\frac {\omega _t}{1+t})$
converges in the Gromov–Hausdorff sense to an r-dimensional torus
![]() $\mathbb T^r$
as
$\mathbb T^r$
as
![]() $t\to \infty $
. The result can be adapted to Oeljeklaus–Toma manifolds of arbitrary type by assuming the initial metric to be left-invariant with respect to the structure of solvmanifold. Moreover, a result of Lauret in [Reference Lauret15, Reference Lauret and Rodríguez Valencia16] allows us to give a characterization of left-invariant Hermitian metrics on an Oeljeklaus–Toma manifold which lift to an algebraic soliton of the Chern–Ricci flow on the universal covering of the manifold (see Proposition 4.1).
$t\to \infty $
. The result can be adapted to Oeljeklaus–Toma manifolds of arbitrary type by assuming the initial metric to be left-invariant with respect to the structure of solvmanifold. Moreover, a result of Lauret in [Reference Lauret15, Reference Lauret and Rodríguez Valencia16] allows us to give a characterization of left-invariant Hermitian metrics on an Oeljeklaus–Toma manifold which lift to an algebraic soliton of the Chern–Ricci flow on the universal covering of the manifold (see Proposition 4.1).
Following the same approach, we focus on the pluriclosed flow on Oeljeklaus–Toma manifolds when the initial pluriclosed Hermitian metric is left-invariant. The pluriclosed flow is a geometric flow of pluriclosed metrics, i.e. of Hermitian metrics having the fundamental form
![]() $\partial \bar \partial $
-closed, introduced by Streets and Tian in [Reference Streets and Tian25]. The flow belongs to the family of the Hermitian curvature flows [Reference Streets and Tian26] and evolves an initial pluriclosed metric along the
$\partial \bar \partial $
-closed, introduced by Streets and Tian in [Reference Streets and Tian25]. The flow belongs to the family of the Hermitian curvature flows [Reference Streets and Tian26] and evolves an initial pluriclosed metric along the
![]() $(1,1)$
-component of the Bismut–Ricci form. Namely, on a Hermitian manifold
$(1,1)$
-component of the Bismut–Ricci form. Namely, on a Hermitian manifold
![]() $(M,\omega )$
, there always exists a unique metric connection
$(M,\omega )$
, there always exists a unique metric connection
![]() $\nabla ^B$
, called the Bismut connection [Reference Bismut4], preserving the complex structure and such that
$\nabla ^B$
, called the Bismut connection [Reference Bismut4], preserving the complex structure and such that
where
![]() $T^B$
is the torsion of
$T^B$
is the torsion of
![]() $\nabla ^B$
. The Bismut–Ricci form of
$\nabla ^B$
. The Bismut–Ricci form of
![]() $\omega $
is then defined as
$\omega $
is then defined as
 $$ \begin{align*}\rho_B(X,Y):=\sqrt{-1}\sum_{i=1}^n R_B(X,Y,X_i,\bar X_i), \end{align*} $$
$$ \begin{align*}\rho_B(X,Y):=\sqrt{-1}\sum_{i=1}^n R_B(X,Y,X_i,\bar X_i), \end{align*} $$
where
![]() $R_B$
is the curvature tensor of
$R_B$
is the curvature tensor of
![]() $\nabla ^B$
and
$\nabla ^B$
and
![]() $\{X_i\}$
is a unitary frame with respect to
$\{X_i\}$
is a unitary frame with respect to
![]() $\omega $
.
$\omega $
.
![]() $\rho _B$
is always a closed real form. Given a pluriclosed Hermitian metric
$\rho _B$
is always a closed real form. Given a pluriclosed Hermitian metric
![]() $\omega $
on M, the pluriclosed flow is then defined as the geometric flow of pluriclosed metrics governed by the equation
$\omega $
on M, the pluriclosed flow is then defined as the geometric flow of pluriclosed metrics governed by the equation
The pluriclosed flow was deeply studied in literature (see, for instance, [Reference Arroyo and Lafuente3, Reference Boling5, Reference Enrietti, Fino and Vezzoni6, Reference Garcia-Fernandez, Jordan and Streets9, Reference Jordan and Streets12, Reference Pujia and Vezzoni19–Reference Streets24, Reference Streets and Tian27] and the references therein).
Our main result is the following theorem.
Theorem 1.1 Let
![]() $\omega $
be a left-invariant pluriclosed Hermitian metric on an Oeljeklaus–Toma manifold M. Then the pluriclosed flow starting from
$\omega $
be a left-invariant pluriclosed Hermitian metric on an Oeljeklaus–Toma manifold M. Then the pluriclosed flow starting from
![]() $\omega $
has a long-time solution
$\omega $
has a long-time solution
![]() $\omega _t$
such that
$\omega _t$
such that
![]() $(M, \frac {\omega _t}{1+t})$
converges in the Gromov–Hausdorff sense to
$(M, \frac {\omega _t}{1+t})$
converges in the Gromov–Hausdorff sense to
![]() $(\mathbb T^s,d)$
. Moreover,
$(\mathbb T^s,d)$
. Moreover,
![]() $\omega $
lifts to an expanding algebraic soliton on the universal covering of M if and only if it is diagonal and the first s diagonal components coincide. Finally,
$\omega $
lifts to an expanding algebraic soliton on the universal covering of M if and only if it is diagonal and the first s diagonal components coincide. Finally,
![]() $(\mathbb H^s\times \mathbb C^s, \frac {\omega _t}{1+t})$
converges in the Cheeger–Gromov sense to
$(\mathbb H^s\times \mathbb C^s, \frac {\omega _t}{1+t})$
converges in the Cheeger–Gromov sense to
![]() $(\mathbb H^s\times \mathbb C^s, \tilde {\omega }_{\infty })$
, where
$(\mathbb H^s\times \mathbb C^s, \tilde {\omega }_{\infty })$
, where
![]() $\tilde {\omega }_{\infty }$
is an algebraic soliton.
$\tilde {\omega }_{\infty }$
is an algebraic soliton.
Here, we recall that a left-invariant Hermitian metric
![]() $\omega $
on a Lie group G with a left-invariant complex structure is an algebraic soliton for a geometric flow of left-invariant Hermitian metrics if
$\omega $
on a Lie group G with a left-invariant complex structure is an algebraic soliton for a geometric flow of left-invariant Hermitian metrics if
![]() $\omega _t=c_t\varphi _t^*(\omega )$
solves the flow, where
$\omega _t=c_t\varphi _t^*(\omega )$
solves the flow, where
![]() $\{c_t\}$
is a positive scaling and
$\{c_t\}$
is a positive scaling and
![]() $\{\varphi _t\}$
is a family of automorphims of G preserving the complex structure. Moreover, the distance d in the statement is the distance induced by
$\{\varphi _t\}$
is a family of automorphims of G preserving the complex structure. Moreover, the distance d in the statement is the distance induced by
![]() $3\omega _{\infty }$
on the torus base of M. Now, we describe the condition diagonal appearing in the statement of Theorem 1.1. The existence of a pluriclosed metric on an Oeljeklaus–Toma manifold imposes some restrictions (see [Reference Angella, Dubickas, Otiman and Stelzig1, Corollary 3]). In particular, the manifold has type
$3\omega _{\infty }$
on the torus base of M. Now, we describe the condition diagonal appearing in the statement of Theorem 1.1. The existence of a pluriclosed metric on an Oeljeklaus–Toma manifold imposes some restrictions (see [Reference Angella, Dubickas, Otiman and Stelzig1, Corollary 3]). In particular, the manifold has type
![]() $(s,s)$
and admits a left-invariant
$(s,s)$
and admits a left-invariant
![]() $(1,0)$
-coframe
$(1,0)$
-coframe
![]() $\{\omega ^1,\dots ,\omega ^s,\gamma ^1,\dots ,\gamma ^s\}$
satisfying
$\{\omega ^1,\dots ,\omega ^s,\gamma ^1,\dots ,\gamma ^s\}$
satisfying
 $$ \begin{align*} \begin{cases} d\omega^k=\frac{\sqrt{-1}}{2}\omega^k\wedge\bar \omega^k,\quad & k=1,\dots,s,\\ d\gamma^i=\sum_{k=1}^s\lambda_{ki}\,\omega^k\wedge \gamma^{i}-\sum_{k=1}^s\,\lambda_{ki}\bar{\omega}^{k}\wedge\gamma^i,\quad& i=1,\dots, s, \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} d\omega^k=\frac{\sqrt{-1}}{2}\omega^k\wedge\bar \omega^k,\quad & k=1,\dots,s,\\ d\gamma^i=\sum_{k=1}^s\lambda_{ki}\,\omega^k\wedge \gamma^{i}-\sum_{k=1}^s\,\lambda_{ki}\bar{\omega}^{k}\wedge\gamma^i,\quad& i=1,\dots, s, \end{cases} \end{align*} $$
with
By
![]() $\omega $
diagonal, we mean that it takes a diagonal form with respect to such a coframe. The first part of Theorem 1.1 in the case of the Inoue–Bombieri surfaces is proved in [Reference Boling5, Corollary 3.18].
$\omega $
diagonal, we mean that it takes a diagonal form with respect to such a coframe. The first part of Theorem 1.1 in the case of the Inoue–Bombieri surfaces is proved in [Reference Boling5, Corollary 3.18].
Theorem 1.1 provides a description of the long-time behavior of the solution
![]() $\omega _t$
to the pluriclosed flow as
$\omega _t$
to the pluriclosed flow as
![]() $t\to \infty $
. For the definition of the convergence in the Gromov–Hausdorff sense, we refer to Section 3, whereas here we briefly recall the definition of convergence in the Cheeger–Gromov sense: a sequence of pointed Riemannian manifolds
$t\to \infty $
. For the definition of the convergence in the Gromov–Hausdorff sense, we refer to Section 3, whereas here we briefly recall the definition of convergence in the Cheeger–Gromov sense: a sequence of pointed Riemannian manifolds
![]() $(M_k, g_k, p_k)$
converges in the Cheeger–Gromov sense to a pointed Riemannian manifold
$(M_k, g_k, p_k)$
converges in the Cheeger–Gromov sense to a pointed Riemannian manifold
![]() $(M,g,p)$
if there exists a sequence of open subsets
$(M,g,p)$
if there exists a sequence of open subsets
![]() $A_k$
of M so that every compact subset of M eventually lies in some
$A_k$
of M so that every compact subset of M eventually lies in some
![]() $A_k$
, and a sequence of smooth maps
$A_k$
, and a sequence of smooth maps
![]() $\phi _k\colon A_k\to M_k $
which are diffeomorphisms onto some open set of
$\phi _k\colon A_k\to M_k $
which are diffeomorphisms onto some open set of
![]() $M_k$
which satisfy
$M_k$
which satisfy
![]() $\phi _k(p_k)=p$
, such that
$\phi _k(p_k)=p$
, such that
See [Reference Lauret14, Section 6] for a deep analysis of Cheeger–Gromov convergence both in the general case and in the homogeneous one and [Reference Lauret15, Section 5.1] for the case of Hermitian Lie groups.
2 Definition of Oeljeklaus–Toma manifolds
We briefly recall the construction of Oeljeklaus–Toma manifolds [Reference Oeljeklaus and Toma17].
Let
![]() $\mathbb {Q}\subseteq \mathbb {K}$
be an algebraic number field with
$\mathbb {Q}\subseteq \mathbb {K}$
be an algebraic number field with
![]() $[\mathbb {K}:\mathbb {Q}]=r+2s$
and
$[\mathbb {K}:\mathbb {Q}]=r+2s$
and
![]() $r,s\ge 1$
. Let
$r,s\ge 1$
. Let
![]() $\sigma _1,\ldots , \sigma _r\colon \mathbb {K}\to \mathbb {R}$
be the real embeddings of
$\sigma _1,\ldots , \sigma _r\colon \mathbb {K}\to \mathbb {R}$
be the real embeddings of
![]() $\mathbb {K}$
and
$\mathbb {K}$
and
![]() $\sigma _{r+1},\ldots ,\sigma _{r+2s}\colon \mathbb {K}\to \mathbb {C}$
be the complex embeddings of
$\sigma _{r+1},\ldots ,\sigma _{r+2s}\colon \mathbb {K}\to \mathbb {C}$
be the complex embeddings of
![]() $\mathbb {K}$
satisfying
$\mathbb {K}$
satisfying
![]() $\sigma _{r+s+i}=\bar \sigma _{r+i},$
for every
$\sigma _{r+s+i}=\bar \sigma _{r+i},$
for every
![]() $ i=1,\ldots , s.$
We denote by
$ i=1,\ldots , s.$
We denote by
![]() $\mathcal {O}_{\mathbb {K}}$
the ring of algebraic integers of
$\mathcal {O}_{\mathbb {K}}$
the ring of algebraic integers of
![]() $\mathbb {K}$
and by
$\mathbb {K}$
and by
![]() $\mathcal {O}_{\mathbb {K}}^*$
the group of units of
$\mathcal {O}_{\mathbb {K}}^*$
the group of units of
![]() $\mathcal {O}_{\mathbb {K}}$
. Let
$\mathcal {O}_{\mathbb {K}}$
. Let
be the group of totally positive units of
![]() $\mathcal {O}_{\mathbb {K}}$
. The groups
$\mathcal {O}_{\mathbb {K}}$
. The groups
![]() $\mathcal {O}_{\mathbb {K}}$
and
$\mathcal {O}_{\mathbb {K}}$
and
![]() $\mathcal {O}_{\mathbb {K}}^{*,+}$
act on
$\mathcal {O}_{\mathbb {K}}^{*,+}$
act on
![]() $\mathbb H^r\times \mathbb C^s$
as
$\mathbb H^r\times \mathbb C^s$
as
 $$ \begin{align*}&a\cdot(z_1,\ldots, z_r,w_1,\ldots, w_s)\\\quad&=(z_1+\sigma_1(a),\ldots, z_r+\sigma_r(a), w_1+\sigma_{r+1}(a),\ldots, w_s+\sigma_{r+s}(a)), \quad \mbox{for all } a\in \mathcal{O}_{\mathbb{K}} \end{align*} $$
$$ \begin{align*}&a\cdot(z_1,\ldots, z_r,w_1,\ldots, w_s)\\\quad&=(z_1+\sigma_1(a),\ldots, z_r+\sigma_r(a), w_1+\sigma_{r+1}(a),\ldots, w_s+\sigma_{r+s}(a)), \quad \mbox{for all } a\in \mathcal{O}_{\mathbb{K}} \end{align*} $$
and
 $$ \begin{align*}&u\cdot(z_1,\ldots, z_r,w_1,\ldots, w_s)\\\quad&=(\sigma_1(u)z_1,\ldots, \sigma_r(u)z_r, \sigma_{r+1}(u)w_1,\ldots, \sigma_{r+s}(u) w_s)\, , \quad \mbox{for every } u\in \mathcal{O}_{\mathbb{K}}^{*,+}. \end{align*} $$
$$ \begin{align*}&u\cdot(z_1,\ldots, z_r,w_1,\ldots, w_s)\\\quad&=(\sigma_1(u)z_1,\ldots, \sigma_r(u)z_r, \sigma_{r+1}(u)w_1,\ldots, \sigma_{r+s}(u) w_s)\, , \quad \mbox{for every } u\in \mathcal{O}_{\mathbb{K}}^{*,+}. \end{align*} $$
There always exists a free subgroup U of rank r of
![]() $\mathcal {O}_{\mathbb {K}}^{*,+}$
such that
$\mathcal {O}_{\mathbb {K}}^{*,+}$
such that
![]() $\mathrm { pr}_{\mathbb {R}^r}\circ l(U)$
is a lattice of rank r in
$\mathrm { pr}_{\mathbb {R}^r}\circ l(U)$
is a lattice of rank r in
![]() $\mathbb {R}^r$
, where
$\mathbb {R}^r$
, where
![]() $l\colon \mathcal {O}_{\mathbb {K}}^{*,+}\to \mathbb {R}^{r+s}$
is the logarithmic representation of units
$l\colon \mathcal {O}_{\mathbb {K}}^{*,+}\to \mathbb {R}^{r+s}$
is the logarithmic representation of units
and
![]() $\mathrm {pr}_{\mathbb {R}^r}\colon \mathbb {R}^{r+s}\to \mathbb {R}^r$
is the projection on the first r coordinates. The action of
$\mathrm {pr}_{\mathbb {R}^r}\colon \mathbb {R}^{r+s}\to \mathbb {R}^r$
is the projection on the first r coordinates. The action of
![]() $U\ltimes \mathcal {O}_{\mathbb {K}}$
on
$U\ltimes \mathcal {O}_{\mathbb {K}}$
on
![]() $\mathbb H^r\times \mathbb C^s$
is free, properly discontinuous, and co-compact. An Oeljeklaus–Toma manifold is then defined as the quotient
$\mathbb H^r\times \mathbb C^s$
is free, properly discontinuous, and co-compact. An Oeljeklaus–Toma manifold is then defined as the quotient
and it is a compact complex manifold having complex dimension
![]() $r+s$
.
$r+s$
.
The structure of torus bundle of an Oeljeklaus–Toma manifold can be seen as follows: we have
and that the action of U on
![]() $\mathbb H^r\times \mathbb C^s$
induces an action on
$\mathbb H^r\times \mathbb C^s$
induces an action on
![]() $\mathbb R_+^{r}\times \mathbb T^{r+2s}$
such that, for every
$\mathbb R_+^{r}\times \mathbb T^{r+2s}$
such that, for every
![]() $x\in \mathbb {\mathbb R}^r_+$
and
$x\in \mathbb {\mathbb R}^r_+$
and
![]() $u\in U$
, the induced map
$u\in U$
, the induced map
is a diffeomorphism. Hence,
inherits the structure of a
![]() $\mathbb T^{r+2s}$
-bundle over
$\mathbb T^{r+2s}$
-bundle over
![]() $\mathbb T^r$
. We denote by
$\mathbb T^r$
. We denote by
![]() $\pi $
and F the projections
$\pi $
and F the projections
From the viewpoint of Lie groups, the universal covering of an Oeljeklaus–Toma manifold M has a natural structure of solvable Lie group G and the complex structure on M lifts to a left-invariant complex structure [Reference Kasuya13]. Therefore, Oeljeklaus–Toma manifolds can be seen as compact solvmanifolds with a left-invariant complex structure. The solvable structure on the universal covering of M can be described in terms of the existence of a left-invariant
![]() $(1,0)$
-coframe
$(1,0)$
-coframe
![]() $\{\omega ^1,\dots ,\omega ^r,\gamma ^1,\dots ,\gamma ^s\}$
such that
$\{\omega ^1,\dots ,\omega ^r,\gamma ^1,\dots ,\gamma ^s\}$
such that
 $$ \begin{align} \begin{cases} d\omega^k=\frac{\sqrt{-1}}{2}\omega^k\wedge\bar \omega^k,\quad & k=1,\dots,r,\\ d\gamma^i=\sum_{k=1}^r\lambda_{ki}\,\omega^k\wedge \gamma^{i}-\sum_{k=1}^r\,\lambda_{ki}\bar{\omega}^{k}\wedge\gamma^i,\quad & i=1,\dots, s, \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} d\omega^k=\frac{\sqrt{-1}}{2}\omega^k\wedge\bar \omega^k,\quad & k=1,\dots,r,\\ d\gamma^i=\sum_{k=1}^r\lambda_{ki}\,\omega^k\wedge \gamma^{i}-\sum_{k=1}^r\,\lambda_{ki}\bar{\omega}^{k}\wedge\gamma^i,\quad & i=1,\dots, s, \end{cases} \end{align} $$
where
and
![]() $b_{ki},c_{ki}\in {\mathbb R}$
depend on the embeddings
$b_{ki},c_{ki}\in {\mathbb R}$
depend on the embeddings
![]() $\sigma _j$
as
$\sigma _j$
as
 $$ \begin{align} \sigma_{r+i}(u)=\left(\prod_{k=1}^r(\sigma_k(u))^{\frac{b_{ki}}{2}}\right)e^{\sqrt{-1}\sum_{k=1}^r c_{ki} \log\sigma_k(u) }, \end{align} $$
$$ \begin{align} \sigma_{r+i}(u)=\left(\prod_{k=1}^r(\sigma_k(u))^{\frac{b_{ki}}{2}}\right)e^{\sqrt{-1}\sum_{k=1}^r c_{ki} \log\sigma_k(u) }, \end{align} $$
for any
![]() $u\in U$
,
$u\in U$
,
![]() $k=1,\dots , r$
and
$k=1,\dots , r$
and
![]() $i=1,\dots , s$
. Since
$i=1,\dots , s$
. Since
![]() $U\subseteq \mathcal {O}_{\mathbb {K}}^*$
, it is easy to see that
$U\subseteq \mathcal {O}_{\mathbb {K}}^*$
, it is easy to see that
 $$ \begin{align*}l(U)\subseteq\left\{x\in {\mathbb R}^{r+s}\quad \middle|\quad \sum_{i=1}^{r+s}x_i=0\right\}. \end{align*} $$
$$ \begin{align*}l(U)\subseteq\left\{x\in {\mathbb R}^{r+s}\quad \middle|\quad \sum_{i=1}^{r+s}x_i=0\right\}. \end{align*} $$
This fact together with (2) implies that, for every
![]() $u\in U$
,
$u\in U$
,
 $$ \begin{align*}\sum_{i=1}^r\log\sigma_i(u)\left(1+\sum_{k=1}^sb_{ik}\right)=0\, , \end{align*} $$
$$ \begin{align*}\sum_{i=1}^r\log\sigma_i(u)\left(1+\sum_{k=1}^sb_{ik}\right)=0\, , \end{align*} $$
which, since
![]() $\mathrm {pr}_{\mathbb {R}^r}\circ l(U)$
is a lattice of rank r in
$\mathrm {pr}_{\mathbb {R}^r}\circ l(U)$
is a lattice of rank r in
![]() $\mathbb {R}^r$
, is equivalent to
$\mathbb {R}^r$
, is equivalent to
 $$ \begin{align} \sum_{k=1}^sb_{ik}=-1,\quad \mbox{for all } i=1,\ldots, r. \end{align} $$
$$ \begin{align} \sum_{k=1}^sb_{ik}=-1,\quad \mbox{for all } i=1,\ldots, r. \end{align} $$
The dual frame
![]() $\{Z_1,\dots , Z_r,W_1,\dots ,W_s\}$
to
$\{Z_1,\dots , Z_r,W_1,\dots ,W_s\}$
to
![]() $\{\omega ^1,\dots ,\omega ^r,\gamma ^1,\dots ,\gamma ^s\}$
satisfies the following structure equations:
$\{\omega ^1,\dots ,\omega ^r,\gamma ^1,\dots ,\gamma ^s\}$
satisfies the following structure equations:
for
![]() $k=1,\dots , r$
and
$k=1,\dots , r$
and
![]() $i=1,\dots , s$
. Consequently, the Lie algebra
$i=1,\dots , s$
. Consequently, the Lie algebra
![]() $\mathfrak {g}$
of the universal covering of M splits as vector space as
$\mathfrak {g}$
of the universal covering of M splits as vector space as
where
![]() $\mathfrak {I}$
is an abelian ideal and
$\mathfrak {I}$
is an abelian ideal and
![]() $\mathfrak {h}$
is a subalgebra isomorphic to
$\mathfrak {h}$
is a subalgebra isomorphic to
 $\underbrace {\mathfrak {f}\oplus \dots \oplus \mathfrak {f}}_{r\mbox {-times}}$
, where
$\underbrace {\mathfrak {f}\oplus \dots \oplus \mathfrak {f}}_{r\mbox {-times}}$
, where
![]() $\mathfrak f$
is the filiform Lie algebra
$\mathfrak f$
is the filiform Lie algebra
![]() $\mathfrak {f}=\langle e_1,e_2\rangle $
,
$\mathfrak {f}=\langle e_1,e_2\rangle $
,
![]() $[e_1,e_2]=-\tfrac 12 e_1$
. The complex structure J induced on
$[e_1,e_2]=-\tfrac 12 e_1$
. The complex structure J induced on
![]() $\mathfrak g$
preserves both
$\mathfrak g$
preserves both
![]() $\mathfrak h$
and
$\mathfrak h$
and
![]() $\mathfrak I$
, and its restriction
$\mathfrak I$
, and its restriction
![]() $J_{\mathfrak h}$
on
$J_{\mathfrak h}$
on
![]() $\mathfrak h$
satisfies
$\mathfrak h$
satisfies
 $$ \begin{align*}J_{\mathfrak{h}}=\underbrace{J_{\mathfrak f}\oplus \dots \oplus J_{\mathfrak f}}_{r\mbox{-times}}\, , \end{align*} $$
$$ \begin{align*}J_{\mathfrak{h}}=\underbrace{J_{\mathfrak f}\oplus \dots \oplus J_{\mathfrak f}}_{r\mbox{-times}}\, , \end{align*} $$
where
![]() $J_{\mathfrak f}$
is the complex structure on
$J_{\mathfrak f}$
is the complex structure on
![]() $\mathfrak f$
defined by
$\mathfrak f$
defined by
![]() $J_{\mathfrak f}(e_1)= e_2$
. Moreover,
$J_{\mathfrak f}(e_1)= e_2$
. Moreover,
3 Convergence in the Gromov–Hausdorff sense
We briefly recall Gromov–Hausdorff convergence of metric spaces. The Gromov–Hausdorff distance between two metric spaces
![]() $(X,d_X)$
,
$(X,d_X)$
,
![]() $(Y,d_Y)$
is the infimum of all positive
$(Y,d_Y)$
is the infimum of all positive
![]() $\epsilon $
for which there exist two functions
$\epsilon $
for which there exist two functions
![]() $F\colon X\to Y$
,
$F\colon X\to Y$
,
![]() $G\colon Y\to X$
, not necessarily continuous, satisfying the following four properties:
$G\colon Y\to X$
, not necessarily continuous, satisfying the following four properties:
for all
![]() $x,x_1,x_2\in X$
and
$x,x_1,x_2\in X$
and
![]() $y,y_1,y_2\in Y$
. If
$y,y_1,y_2\in Y$
. If
![]() $\{d_t\}_{t\in [0,\infty )}$
is a one-parameter family of distances on X,
$\{d_t\}_{t\in [0,\infty )}$
is a one-parameter family of distances on X,
![]() $(X,d_t)$
converges to
$(X,d_t)$
converges to
![]() $(Y,d_Y)$
in the Gromov–Hausdorff sense if the Gromov–Hausdorff distance between
$(Y,d_Y)$
in the Gromov–Hausdorff sense if the Gromov–Hausdorff distance between
![]() $(X,d_t)$
and
$(X,d_t)$
and
![]() $(Y,d)$
tends to
$(Y,d)$
tends to
![]() $0$
as
$0$
as
![]() $t\to \infty $
.
$t\to \infty $
.
Let
![]() $\{\omega _t\}_{t\in [0,\infty )}$
be a smooth curve of Hermitian metrics on an Oeljeklaus–Toma manifold, and let
$\{\omega _t\}_{t\in [0,\infty )}$
be a smooth curve of Hermitian metrics on an Oeljeklaus–Toma manifold, and let
![]() $d_t$
be the induced distance on M. For a smooth curve
$d_t$
be the induced distance on M. For a smooth curve
![]() $\gamma $
on M, let
$\gamma $
on M, let
![]() $L_t(\gamma )$
be the length of
$L_t(\gamma )$
be the length of
![]() $\gamma $
with respect to
$\gamma $
with respect to
![]() $\omega _t$
. We further denote by
$\omega _t$
. We further denote by
![]() $\mathcal H$
the foliation induced by
$\mathcal H$
the foliation induced by
![]() $\mathfrak h$
on M.
$\mathfrak h$
on M.
Proposition 3.1 Let
![]() $\{\omega _t\}_{t\in [0,\infty )}$
be a smooth curve of Hermitian metrics on an Oeljeklaus–Toma manifold such that
$\{\omega _t\}_{t\in [0,\infty )}$
be a smooth curve of Hermitian metrics on an Oeljeklaus–Toma manifold such that
pointwise. Assume that there exist
![]() $T\in (0,\infty )$
and
$T\in (0,\infty )$
and
![]() $C>0$
such that:
$C>0$
such that:
-
1.
 $L_t(\gamma )\leq C L_0(\gamma ),$
for every smooth curve
$L_t(\gamma )\leq C L_0(\gamma ),$
for every smooth curve
 $\gamma $
in M.
$\gamma $
in M. -
2.
 $L_t(\gamma )\leq (C/\sqrt {t})L_0(\gamma )$
, for every smooth curve
$L_t(\gamma )\leq (C/\sqrt {t})L_0(\gamma )$
, for every smooth curve
 $\gamma $
in M such that
$\gamma $
in M such that
 $\dot \gamma \in \ker \omega _\infty $
.
$\dot \gamma \in \ker \omega _\infty $
.
Assume further that:
-
3. For every
 $\epsilon ,\ell>0$
, there exists
$\epsilon ,\ell>0$
, there exists
 $T>0$
such that
$T>0$
such that
 $|L_t(\gamma )-L_{\infty }(\gamma )|<\epsilon $
, for every
$|L_t(\gamma )-L_{\infty }(\gamma )|<\epsilon $
, for every
 $t>T$
and every curve
$t>T$
and every curve
 $\gamma $
in M tangent to
$\gamma $
in M tangent to
 $\mathcal H$
and such that
$\mathcal H$
and such that
 $L_\infty (\gamma )<\ell $
.
$L_\infty (\gamma )<\ell $
.
Then
![]() $(M,d_t)$
converges in the Gromov–Hausdorff sense to
$(M,d_t)$
converges in the Gromov–Hausdorff sense to
![]() $(\mathbb T^{r},d)$
, where d is the distance induced by
$(\mathbb T^{r},d)$
, where d is the distance induced by
![]() $\omega _{\infty }$
onto
$\omega _{\infty }$
onto
![]() $\mathbb T^{r}$
.
$\mathbb T^{r}$
.
Proof We follow the approach in [Reference Tosatti and Weinkove28, Section 5] and in [Reference Zheng32, Proof of Theorem 1.1]. Let M be an Oeljeklaus–Toma manifold. Consider the structure of M as
![]() $\mathbb T^{r+2s}$
-bundle over a
$\mathbb T^{r+2s}$
-bundle over a
![]() $\mathbb T^{r}$
. Let
$\mathbb T^{r}$
. Let
![]() $F\colon M\to \mathbb T^{r}$
be the projection onto the base, and let
$F\colon M\to \mathbb T^{r}$
be the projection onto the base, and let
![]() $G\colon \mathbb T^{r}\to M$
be an arbitrary map such that
$G\colon \mathbb T^{r}\to M$
be an arbitrary map such that
![]() $F\circ G=\mathrm {Id}_{\mathbb T^{r}}$
. We show that, for every
$F\circ G=\mathrm {Id}_{\mathbb T^{r}}$
. We show that, for every
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $T>0$
such that
$T>0$
such that
for every
![]() $t\geq T$
,
$t\geq T$
,
![]() $p,q\in M$
,
$p,q\in M$
,
![]() $a,b\in \mathbb T^r$
, which implies the statement.
$a,b\in \mathbb T^r$
, which implies the statement.
Note that (7) is trivial since
for every
![]() $a\in \mathbb T^r$
.
$a\in \mathbb T^r$
.
Then we show that (6) is satisfied. Let
![]() $p,q\in M$
be two points in the same fiber over
$p,q\in M$
be two points in the same fiber over
![]() $\mathbb T^r$
. Assume that
$\mathbb T^r$
. Assume that
![]() $p=\pi (z,w)$
. We denote with
$p=\pi (z,w)$
. We denote with
![]() $\mathcal {L}_{(z,w)}$
the leaf of the foliation
$\mathcal {L}_{(z,w)}$
the leaf of the foliation
![]() $\ker \omega _{\infty }$
on the universal covering of M passing through
$\ker \omega _{\infty }$
on the universal covering of M passing through
![]() $(z,w)$
. We easily see that, for all
$(z,w)$
. We easily see that, for all
![]() $(z,w)\in \mathbb H^r\times \mathbb C^s$
,
$(z,w)\in \mathbb H^r\times \mathbb C^s$
,
![]() $\mathcal {L}_{(z,w)}=\{z\}\times \mathbb C^s$
. In view of [Reference Verbitsky30, Section 2], for every
$\mathcal {L}_{(z,w)}=\{z\}\times \mathbb C^s$
. In view of [Reference Verbitsky30, Section 2], for every
![]() $z\in \mathbb H^r$
,
$z\in \mathbb H^r$
,
![]() $\pi (\{z\}\times \mathbb C^s)$
is the leaf of the foliation
$\pi (\{z\}\times \mathbb C^s)$
is the leaf of the foliation
![]() $\ker \omega _{\infty }$
on M passing through p and it is dense in the fiber
$\ker \omega _{\infty }$
on M passing through p and it is dense in the fiber
![]() $F^{-1}(F(p))$
. Let
$F^{-1}(F(p))$
. Let
![]() $B_{R}$
be the standard ball in
$B_{R}$
be the standard ball in
![]() $\mathbb C^s$
about the origin having radius R. We can choose R so that every point in
$\mathbb C^s$
about the origin having radius R. We can choose R so that every point in
![]() $F^{-1}(F(p))$
has distance with respect to
$F^{-1}(F(p))$
has distance with respect to
![]() $d_0$
less than
$d_0$
less than
![]() $\epsilon /2C$
to
$\epsilon /2C$
to
![]() $\pi (\{z\}\times \bar B_{R})$
. On the other hand, given two points in
$\pi (\{z\}\times \bar B_{R})$
. On the other hand, given two points in
![]() $\pi (\{z\}\times \bar B_{R})$
, they can be joined with a curve
$\pi (\{z\}\times \bar B_{R})$
, they can be joined with a curve
![]() $\gamma $
in
$\gamma $
in
![]() $F^{-1}(F(p))$
which is tangent to
$F^{-1}(F(p))$
which is tangent to
![]() $\ker \omega _\infty $
. Hence, for any such curve, condition 2 implies
$\ker \omega _\infty $
. Hence, for any such curve, condition 2 implies
 $$ \begin{align*}L_t(\gamma)\leq \frac{C'}{\sqrt t}, \end{align*} $$
$$ \begin{align*}L_t(\gamma)\leq \frac{C'}{\sqrt t}, \end{align*} $$
for a uniform constant
![]() $C'$
depending only on R. Let
$C'$
depending only on R. Let
![]() $p_0=\pi (z,0)$
, let
$p_0=\pi (z,0)$
, let
![]() $\gamma _1$
be a curve in
$\gamma _1$
be a curve in
![]() $F^{-1}(F(p))$
connecting p with
$F^{-1}(F(p))$
connecting p with
![]() $p_0$
tangent to
$p_0$
tangent to
![]() $\ker \omega _\infty $
, and let
$\ker \omega _\infty $
, and let
![]() $\gamma _2$
be a curve connecting
$\gamma _2$
be a curve connecting
![]() $p_0$
with q having minimal length with respect to
$p_0$
with q having minimal length with respect to
![]() $d_0$
. Hence, by using condition 1, for t sufficiently large, we have
$d_0$
. Hence, by using condition 1, for t sufficiently large, we have
 $$ \begin{align*}d_t(p,q)\leq L_{t}(\gamma_1)+L_t(\gamma_2)\leq \frac{C'}{\sqrt{t}}+CL_{0}(\gamma_2)\leq \frac{C'}{\sqrt{t}}+\frac{\epsilon}{2}\leq \epsilon, \end{align*} $$
$$ \begin{align*}d_t(p,q)\leq L_{t}(\gamma_1)+L_t(\gamma_2)\leq \frac{C'}{\sqrt{t}}+CL_{0}(\gamma_2)\leq \frac{C'}{\sqrt{t}}+\frac{\epsilon}{2}\leq \epsilon, \end{align*} $$
i.e.,
and (6) follows.
Next, we show (4) and (5). First of all, we denote with g the Riemannian metric on
![]() $\mathbb {T}^r$
induced by
$\mathbb {T}^r$
induced by
![]() $\omega _{\infty }$
, for an explicit expression of g (see [Reference Zheng32, Section 2]), and we observe that
$\omega _{\infty }$
, for an explicit expression of g (see [Reference Zheng32, Section 2]), and we observe that
and the equality holds if and only if
 $$ \begin{align*}\dot \gamma\in\mathcal{Y}=\mathrm{span}_{{\mathbb C}}\left\{ \frac{1}{2\sqrt{-1}}\left(Z_i-\bar Z_i\right)\quad \middle | \quad i=1,\ldots, r \right\}. \end{align*} $$
$$ \begin{align*}\dot \gamma\in\mathcal{Y}=\mathrm{span}_{{\mathbb C}}\left\{ \frac{1}{2\sqrt{-1}}\left(Z_i-\bar Z_i\right)\quad \middle | \quad i=1,\ldots, r \right\}. \end{align*} $$
Let
![]() $p,q\in M$
. We can find a curve
$p,q\in M$
. We can find a curve
![]() $\gamma $
in M connecting p with a point
$\gamma $
in M connecting p with a point
![]() $\tilde {q}$
in the
$\tilde {q}$
in the
![]() $\mathbb T^{r+2s}$
-fiber containing q which is tangent to
$\mathbb T^{r+2s}$
-fiber containing q which is tangent to
![]() $\mathcal Y$
and such that
$\mathcal Y$
and such that
![]() $F(\gamma )$
is a minimal geodesic on
$F(\gamma )$
is a minimal geodesic on
![]() $(\mathbb T^r,g)$
(see, for instance, [Reference Tosatti and Weinkove28, Proof of Theorem 5.1] or [Reference Zheng32, Proof of Theorem 1.1]). By applying condition 3, we have
$(\mathbb T^r,g)$
(see, for instance, [Reference Tosatti and Weinkove28, Proof of Theorem 5.1] or [Reference Zheng32, Proof of Theorem 1.1]). By applying condition 3, we have
 $$ \begin{align*}&d_t(p,q)\leq d_t(p,\tilde q)+d_t(\tilde q,q)\leq d_t(p,\tilde q)+\epsilon\leq L_{t}( \gamma)+\epsilon\leq L_{\infty}(\gamma) +2\epsilon\\&\quad= L_g(F(\gamma))+ 2\epsilon=d(F(p),F(q))+2\epsilon, \end{align*} $$
$$ \begin{align*}&d_t(p,q)\leq d_t(p,\tilde q)+d_t(\tilde q,q)\leq d_t(p,\tilde q)+\epsilon\leq L_{t}( \gamma)+\epsilon\leq L_{\infty}(\gamma) +2\epsilon\\&\quad= L_g(F(\gamma))+ 2\epsilon=d(F(p),F(q))+2\epsilon, \end{align*} $$
for t big enough, i.e.,
for t sufficiently large.
Next, using again (8), we obtain, for
![]() $p,q\in M$
,
$p,q\in M$
,
for t big enough, where
![]() $\gamma $
is a curve which realizes the distance
$\gamma $
is a curve which realizes the distance
![]() $d_t(p, q)$
. Hence, we obtain
$d_t(p, q)$
. Hence, we obtain
By substituting
![]() $p=G(a)$
and
$p=G(a)$
and
![]() $q=G(b)$
in (9) and (10), we infer
$q=G(b)$
in (9) and (10), we infer
4 The left-invariant Chern–Ricci flow on Oeljeklaus–Toma manifolds
Given a Hermitian manifold
![]() $(M,\omega )$
, the Chern connection of
$(M,\omega )$
, the Chern connection of
![]() $\omega $
is the unique connection
$\omega $
is the unique connection
![]() $\nabla $
on
$\nabla $
on
![]() $(M,\omega )$
preserving both
$(M,\omega )$
preserving both
![]() $\omega $
and the complex structure such that the
$\omega $
and the complex structure such that the
![]() $(1,1)$
-component of its torsion tensor is vanishing. The Chern–Ricci form of
$(1,1)$
-component of its torsion tensor is vanishing. The Chern–Ricci form of
![]() $\omega $
is the real closed
$\omega $
is the real closed
![]() $(1,1)$
-form
$(1,1)$
-form
 $$ \begin{align*}\rho_C(X,Y):=\sqrt{-1}\sum_{i=1}^n R_C(X,Y,X_i,\bar X_i), \end{align*} $$
$$ \begin{align*}\rho_C(X,Y):=\sqrt{-1}\sum_{i=1}^n R_C(X,Y,X_i,\bar X_i), \end{align*} $$
where
![]() $R_C$
is the curvature tensor of
$R_C$
is the curvature tensor of
![]() $\nabla $
and
$\nabla $
and
![]() $\{X_i\}$
is a unitary frame with respect to
$\{X_i\}$
is a unitary frame with respect to
![]() $\omega $
. The Chern–Ricci flow is then defined as the geometric flow
$\omega $
. The Chern–Ricci flow is then defined as the geometric flow
In this section, we prove the following Proposition.
Proposition 4.1 Let
![]() $\omega $
be a left-invariant Hermitian metric on an Oeljeklaus–Toma manifold M. Then
$\omega $
be a left-invariant Hermitian metric on an Oeljeklaus–Toma manifold M. Then
![]() $\omega $
lifts to an expanding algebraic soliton for the Chern–Ricci flow on the universal covering of M if and only if it takes the following expression with respect to the coframe
$\omega $
lifts to an expanding algebraic soliton for the Chern–Ricci flow on the universal covering of M if and only if it takes the following expression with respect to the coframe
![]() $\{\omega ^1,\dots ,\omega ^r,\gamma ^1,\dots ,\gamma ^s\}$
satisfying (
1
):
$\{\omega ^1,\dots ,\omega ^r,\gamma ^1,\dots ,\gamma ^s\}$
satisfying (
1
):
 $$ \begin{align} \omega=\sqrt{-1}\left(A\sum_{i=1}^r\omega^i\wedge\bar \omega^i+\sum_{i,j=1}^sg_{r+i\overline{r+j}}\gamma^i\wedge\bar\gamma^j\right). \end{align} $$
$$ \begin{align} \omega=\sqrt{-1}\left(A\sum_{i=1}^r\omega^i\wedge\bar \omega^i+\sum_{i,j=1}^sg_{r+i\overline{r+j}}\gamma^i\wedge\bar\gamma^j\right). \end{align} $$
Moreover, the Chern–Ricci flow starting from
![]() $\omega $
has a long-time solution
$\omega $
has a long-time solution
![]() $\{\omega _t\}$
such that
$\{\omega _t\}$
such that
![]() $(M, \frac {\omega _t}{1+t})$
converges as
$(M, \frac {\omega _t}{1+t})$
converges as
![]() $t\to \infty $
in the Gromov–Hausdorff sense to
$t\to \infty $
in the Gromov–Hausdorff sense to
![]() $(\mathbb T^r,d)$
, where d is the distance induced by
$(\mathbb T^r,d)$
, where d is the distance induced by
![]() $\omega _{\infty }$
onto
$\omega _{\infty }$
onto
![]() $\mathbb T^{r}$
. Finally,
$\mathbb T^{r}$
. Finally,
![]() $(\mathbb H^r\times {\mathbb C}^s, \frac {\omega _t}{1+t})$
converges in the Cheeger–Gromov sense to
$(\mathbb H^r\times {\mathbb C}^s, \frac {\omega _t}{1+t})$
converges in the Cheeger–Gromov sense to
![]() $(\mathbb H^r\times {\mathbb C}^s, \tilde {\omega }_{\infty })$
, where
$(\mathbb H^r\times {\mathbb C}^s, \tilde {\omega }_{\infty })$
, where
![]() $\tilde {\omega }_{\infty }$
is an algebraic soliton.
$\tilde {\omega }_{\infty }$
is an algebraic soliton.
The proof of Proposition 4.1 is based on the following theorem of Lauret.
Theorem 4.2 (Lauret [Reference Lauret15])
Let
![]() $(G,J)$
be a Lie group with a left-invariant complex structure. Then the Chern–Ricci form of a left-invariant Hermitian metric
$(G,J)$
be a Lie group with a left-invariant complex structure. Then the Chern–Ricci form of a left-invariant Hermitian metric
![]() $\omega $
on
$\omega $
on
![]() $(G,J)$
does not depend on the Hermitian metric. Moreover, if
$(G,J)$
does not depend on the Hermitian metric. Moreover, if
![]() $P\ne 0 $
is the endomorphism associated with
$P\ne 0 $
is the endomorphism associated with
![]() $\rho _C$
with respect to
$\rho _C$
with respect to
![]() $\omega $
, then the following are equivalent:
$\omega $
, then the following are equivalent:
-
(1)
 $\omega $
is an algebraic soliton of the Chern–Ricci flow.
$\omega $
is an algebraic soliton of the Chern–Ricci flow. -
(2)
 $P=cI + D$
, for some
$P=cI + D$
, for some
 $D\in \mathrm {Der}(\mathfrak {g}).$
$D\in \mathrm {Der}(\mathfrak {g}).$
-
(3) The eigenvalues of P are either
 $0$
or c, for some
$0$
or c, for some
 $c\in {\mathbb R}$
with
$c\in {\mathbb R}$
with
 $c\neq 0$
,
$c\neq 0$
,
 $\ker P$
is an abelian ideal of the Lie algebra of G, and
$\ker P$
is an abelian ideal of the Lie algebra of G, and
 $(\ker P)^\perp $
is a subalgebra.
$(\ker P)^\perp $
is a subalgebra.
Proof of Proposition 4.1
Let M be an Oeljeklaus–Toma manifold. Since the Chern–Ricci form does not depend on the choice of the left-invariant Hermitian metric, it is enough to compute
![]() $\rho _C$
for the “canonical metric”
$\rho _C$
for the “canonical metric”
 $$ \begin{align} \omega=\sqrt{-1}\left(\sum_{i=1}^r\omega^i\wedge\bar\omega^i+\sum_{j=1}^s\gamma^j\wedge\bar \gamma^j\right). \end{align} $$
$$ \begin{align} \omega=\sqrt{-1}\left(\sum_{i=1}^r\omega^i\wedge\bar\omega^i+\sum_{j=1}^s\gamma^j\wedge\bar \gamma^j\right). \end{align} $$
We recall that the Chern–Ricci form of a left-invariant Hermitian metric
![]() $\omega =\sqrt {-1}\sum _{a=1}^n \alpha ^a\wedge \bar \alpha ^a $
on a Lie group
$\omega =\sqrt {-1}\sum _{a=1}^n \alpha ^a\wedge \bar \alpha ^a $
on a Lie group
![]() $G^{2n}$
with a left-invariant complex structure takes the following algebraic expression:
$G^{2n}$
with a left-invariant complex structure takes the following algebraic expression:
 $$ \begin{align} \rho_C(X,Y) = -\sum_{a=1}^n (\omega([[X,Y]^{0,1},X_a],\bar X_a) + \omega ([[X,Y]^{1,0},\bar X_a],X_a ) ) \, , \end{align} $$
$$ \begin{align} \rho_C(X,Y) = -\sum_{a=1}^n (\omega([[X,Y]^{0,1},X_a],\bar X_a) + \omega ([[X,Y]^{1,0},\bar X_a],X_a ) ) \, , \end{align} $$
for every left-invariant vector fields
![]() $X,Y$
on G, where
$X,Y$
on G, where
![]() $\{\alpha ^i\}$
is a left-invariant unitary
$\{\alpha ^i\}$
is a left-invariant unitary
![]() $(1,0)$
-coframe with dual frame
$(1,0)$
-coframe with dual frame
![]() $\{X_a\}$
(see, e.g., [Reference Vezzoni31]). By applying (13) to the canonical metric (12), we have
$\{X_a\}$
(see, e.g., [Reference Vezzoni31]). By applying (13) to the canonical metric (12), we have
 $$ \begin{align*} \rho_C(X,Y) &=- \sum_{a=1}^r \{ \omega([[X,Y]^{0,1},Z_a],\bar Z_a) + \omega([[X,Y]^{1,0},\bar Z_a],Z_a ) \}\\ &\quad- \sum_{b=1}^s \{ \omega([[X,Y]^{0,1},W_b],\bar W_b) +\omega([[X,Y]^{1,0},\bar W_b],W_b ) \}. \end{align*} $$
$$ \begin{align*} \rho_C(X,Y) &=- \sum_{a=1}^r \{ \omega([[X,Y]^{0,1},Z_a],\bar Z_a) + \omega([[X,Y]^{1,0},\bar Z_a],Z_a ) \}\\ &\quad- \sum_{b=1}^s \{ \omega([[X,Y]^{0,1},W_b],\bar W_b) +\omega([[X,Y]^{1,0},\bar W_b],W_b ) \}. \end{align*} $$
Clearly,
Moreover, since
![]() $\mathfrak {J}$
is an abelian ideal and
$\mathfrak {J}$
is an abelian ideal and
![]() $\omega $
makes
$\omega $
makes
![]() $\mathfrak {J}$
and
$\mathfrak {J}$
and
![]() $\mathfrak {h}$
orthogonal, we have
$\mathfrak {h}$
orthogonal, we have
Moreover, we have
and
which imply
 $$ \begin{align*}\rho_C(Z_i,\bar Z_i)=-\sqrt{-1}\left(\frac12+\sum_{b=1}^s\Im\mathfrak{m}(\lambda_{ib})\right)=-\frac{\sqrt{-1}}{4}, \end{align*} $$
$$ \begin{align*}\rho_C(Z_i,\bar Z_i)=-\sqrt{-1}\left(\frac12+\sum_{b=1}^s\Im\mathfrak{m}(\lambda_{ib})\right)=-\frac{\sqrt{-1}}{4}, \end{align*} $$
and, consequently,
where
![]() $\omega _{\infty }$
is the degenerate metric induced on M by the Poincaré metric on
$\omega _{\infty }$
is the degenerate metric induced on M by the Poincaré metric on
![]() $\mathbb {H}^r$
, namely,
$\mathbb {H}^r$
, namely,
 $$ \begin{align*}\omega_{\infty}=\frac{\sqrt{-1}}{4}\sum_{i=1}^r\omega^i\wedge\bar\omega^i. \end{align*} $$
$$ \begin{align*}\omega_{\infty}=\frac{\sqrt{-1}}{4}\sum_{i=1}^r\omega^i\wedge\bar\omega^i. \end{align*} $$
In general, we have that
 $$ \begin{align*}P_i^j=(\rho_C)_{i\bar k }g^{\bar k j }=\begin{cases}-\frac14g^{\bar i j }, &\quad \mbox{if }i\in\{1,\ldots, r\},\\ 0, &\quad \mbox{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*}P_i^j=(\rho_C)_{i\bar k }g^{\bar k j }=\begin{cases}-\frac14g^{\bar i j }, &\quad \mbox{if }i\in\{1,\ldots, r\},\\ 0, &\quad \mbox{otherwise}. \end{cases} \end{align*} $$
Then part (3) of Theorem 4.2 readily implies that any left-invariant Hermitian metrics of the form (11) lifts to an expanding algebraic soliton on the universal covering of M with cosmological constant
![]() $c=\frac {1}{4A}$
. Conversely, let
$c=\frac {1}{4A}$
. Conversely, let
![]() $\omega $
be an algebraic soliton for the Chern–Ricci flow. Then, thanks to part (2) of Theorem 4.2, we have that
$\omega $
be an algebraic soliton for the Chern–Ricci flow. Then, thanks to part (2) of Theorem 4.2, we have that
On the other hand, we can easily see that, if
![]() $ D\in \mathrm {Der}(\mathfrak {g})$
, then
$ D\in \mathrm {Der}(\mathfrak {g})$
, then
![]() $\mathfrak h \subseteq \ker D$
(see the proof of Corollary 5.4 for the details). This readily implies that
$\mathfrak h \subseteq \ker D$
(see the proof of Corollary 5.4 for the details). This readily implies that
from which the claim follows.
Moreover, the Chern–Ricci flow evolves an arbitrary left-invariant Hermitian metric
![]() $\omega $
as
$\omega $
as
![]() $\omega _t=\omega +t\omega _\infty $
and
$\omega _t=\omega +t\omega _\infty $
and
![]() $\frac {\omega _t}{1+t}\to \omega _\infty $
as
$\frac {\omega _t}{1+t}\to \omega _\infty $
as
![]() $t\to \infty $
. In order to obtain the claim regarding the Gromov–Hausdorff convergence, we show that
$t\to \infty $
. In order to obtain the claim regarding the Gromov–Hausdorff convergence, we show that
![]() $\frac {\omega _t}{1+t}$
satisfies conditions 1–3 in Proposition 3.1. Here, we denote by
$\frac {\omega _t}{1+t}$
satisfies conditions 1–3 in Proposition 3.1. Here, we denote by
![]() $|\cdot |_t$
the norm induced by
$|\cdot |_t$
the norm induced by
![]() $\omega _t$
.
$\omega _t$
.
Condition 2 is trivially satisfied since
![]() $\omega _{t|\mathfrak I\oplus \mathfrak I}=\omega _0$
, for every
$\omega _{t|\mathfrak I\oplus \mathfrak I}=\omega _0$
, for every
![]() $t\geq 0$
, and
$t\geq 0$
, and
for every curve
![]() $\gamma $
in M tangent to
$\gamma $
in M tangent to
![]() $\ker \omega _\infty $
.
$\ker \omega _\infty $
.
On the other hand, for a vector
![]() $v\in \mathfrak h$
, we have
$v\in \mathfrak h$
, we have
for a constant
![]() $C>0$
independent on v. This, together with condition 2, guarantees condition 1.
$C>0$
independent on v. This, together with condition 2, guarantees condition 1.
In order to prove condition 3, let
![]() $\epsilon , \ell>0$
and
$\epsilon , \ell>0$
and
![]() $T>0$
be such that
$T>0$
be such that
 $$ \begin{align*}\left\vert \frac{|v|_t}{\sqrt{1+t}}-|v|_\infty\right\vert\leq \frac{\epsilon}{\ell}, \end{align*} $$
$$ \begin{align*}\left\vert \frac{|v|_t}{\sqrt{1+t}}-|v|_\infty\right\vert\leq \frac{\epsilon}{\ell}, \end{align*} $$
for every
![]() $v\in \mathfrak h$
and
$v\in \mathfrak h$
and
![]() $t\geq T$
. Let
$t\geq T$
. Let
![]() $\gamma $
be a curve in M tangent to
$\gamma $
be a curve in M tangent to
![]() $\mathcal H$
which is parametrized by arclength with respect to
$\mathcal H$
which is parametrized by arclength with respect to
![]() $\omega _\infty $
and such that
$\omega _\infty $
and such that
![]() $L_{\infty }(\gamma )<\ell $
. Then
$L_{\infty }(\gamma )<\ell $
. Then
 $$ \begin{align*}|L_{t}(\gamma)-L_{\infty}(\gamma)|\leq \int_{0}^{b}\left\vert\frac{1}{\sqrt{1+t}}|\dot \gamma |_t-|\dot \gamma|_\infty\right\vert da\leq \frac{\epsilon}{\ell}b\leq \epsilon, \end{align*} $$
$$ \begin{align*}|L_{t}(\gamma)-L_{\infty}(\gamma)|\leq \int_{0}^{b}\left\vert\frac{1}{\sqrt{1+t}}|\dot \gamma |_t-|\dot \gamma|_\infty\right\vert da\leq \frac{\epsilon}{\ell}b\leq \epsilon, \end{align*} $$
since
![]() $b\leq \ell $
.
$b\leq \ell $
.
For the last statement, we identify
![]() $\omega _t$
with its pullback onto
$\omega _t$
with its pullback onto
![]() $\mathbb H^r\times \mathbb C^s$
and we fix as base point the identity element of
$\mathbb H^r\times \mathbb C^s$
and we fix as base point the identity element of
![]() $\mathbb H^r\times \mathbb C^s$
. First, we observe that the endomorphism D represented with respect to the frame
$\mathbb H^r\times \mathbb C^s$
. First, we observe that the endomorphism D represented with respect to the frame
![]() $\{Z_1,\ldots , Z_r, W_1,\ldots , W_s\}$
by the following matrix
$\{Z_1,\ldots , Z_r, W_1,\ldots , W_s\}$
by the following matrix
 $$ \begin{align*}\begin{pmatrix} 0&0\\0& \mathrm{I}_{\mathfrak J} \end{pmatrix} \end{align*} $$
$$ \begin{align*}\begin{pmatrix} 0&0\\0& \mathrm{I}_{\mathfrak J} \end{pmatrix} \end{align*} $$
is a derivation of
![]() $\mathfrak {g}$
. Moreover, we can construct
$\mathfrak {g}$
. Moreover, we can construct
 $$ \begin{align*}\exp(s(t)D)=\begin{pmatrix}\mathrm{I}_{\mathfrak{h}}& 0 \\ 0 & e^{s(t)}\mathrm{ I}_{\mathfrak{J}}\end{pmatrix}\in \mathrm{Aut}(\mathfrak{g}, J), \quad \mbox{for every } t\ge 0, \end{align*} $$
$$ \begin{align*}\exp(s(t)D)=\begin{pmatrix}\mathrm{I}_{\mathfrak{h}}& 0 \\ 0 & e^{s(t)}\mathrm{ I}_{\mathfrak{J}}\end{pmatrix}\in \mathrm{Aut}(\mathfrak{g}, J), \quad \mbox{for every } t\ge 0, \end{align*} $$
where
![]() $s(t)=\log (\sqrt {1+t})$
and define the one-parameter family
$s(t)=\log (\sqrt {1+t})$
and define the one-parameter family
![]() $\{\varphi _t\}\subseteq \mathrm {Aut}(\mathbb H^r\times {\mathbb C} ^s, J )$
such that
$\{\varphi _t\}\subseteq \mathrm {Aut}(\mathbb H^r\times {\mathbb C} ^s, J )$
such that
Trivially, we see that
 $$ \begin{align*}\begin{aligned} \varphi_t^*\frac{\omega_t}{1+t}(Z_i,\bar Z_j)=&\, \sqrt{-1}\frac{1}{1+t}\left(g_{i\bar j }+\frac t4\delta_{ij}\right )\to \frac{\sqrt{-1}}{4}\delta_{ij} \quad \mbox{as }t\to\infty,\\ \varphi_t^*\frac{\omega_t}{1+t}(Z_i,\bar W_j)=&\,\sqrt{-1}\frac{e^{s(t)}}{1+t}g_{i\overline{r+j}}\to 0 \quad \mbox{as }t\to\infty,\\ \varphi_t^*\frac{\omega_t}{1+t}(W_i,\bar W_j)=&\,\sqrt{-1}\frac{e^{2s(t)}}{1+t}g_{r+i\overline{r+j}} \to \sqrt{-1}g_{r+i\overline{r+j}} \quad \mbox{as }t\to\infty.\\ \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \varphi_t^*\frac{\omega_t}{1+t}(Z_i,\bar Z_j)=&\, \sqrt{-1}\frac{1}{1+t}\left(g_{i\bar j }+\frac t4\delta_{ij}\right )\to \frac{\sqrt{-1}}{4}\delta_{ij} \quad \mbox{as }t\to\infty,\\ \varphi_t^*\frac{\omega_t}{1+t}(Z_i,\bar W_j)=&\,\sqrt{-1}\frac{e^{s(t)}}{1+t}g_{i\overline{r+j}}\to 0 \quad \mbox{as }t\to\infty,\\ \varphi_t^*\frac{\omega_t}{1+t}(W_i,\bar W_j)=&\,\sqrt{-1}\frac{e^{2s(t)}}{1+t}g_{r+i\overline{r+j}} \to \sqrt{-1}g_{r+i\overline{r+j}} \quad \mbox{as }t\to\infty.\\ \end{aligned} \end{align*} $$
These facts guarantee that
hence, the assertion follows.
5 Proof of the main result
In this section, we prove Theorem 1.1.
The existence of pluriclosed metrics on Oeljeklaus–Toma manifolds was studied in [Reference Angella, Dubickas, Otiman and Stelzig1, Reference Fino, Kasuya and Vezzoni8, Reference Otiman18]. In particular, from [Reference Angella, Dubickas, Otiman and Stelzig1] it follows the following result.
Theorem 5.1 ([Reference Angella, Dubickas, Otiman and Stelzig1, Corollary 3])
An Oeljeklaus–Toma manifold of type
![]() $(r,s)$
admits a pluriclosed metric if and only if
$(r,s)$
admits a pluriclosed metric if and only if
![]() $r=s$
and
$r=s$
and
Condition (14) in the previous theorem can be rewritten in terms of the structure constants appearing in (1). Indeed, (1) together with (14) forces
![]() $b_{ki}\in \{0,-1\}$
and
$b_{ki}\in \{0,-1\}$
and
![]() $b_{ki}b_{li}=0$
, for every
$b_{ki}b_{li}=0$
, for every
![]() $i,k,l=1,\dots , s$
with
$i,k,l=1,\dots , s$
with
![]() $k\neq l$
. In particular, using (3), for every fixed index
$k\neq l$
. In particular, using (3), for every fixed index
![]() $k\in \{1,\ldots , s\}$
, there exists a unique
$k\in \{1,\ldots , s\}$
, there exists a unique
![]() $i_k\in \{1,\ldots , s\}$
such that
$i_k\in \{1,\ldots , s\}$
such that
for all
![]() $i\ne i_k$
and, if
$i\ne i_k$
and, if
![]() $k\ne l ,$
then
$k\ne l ,$
then
![]() $i_k\ne i_l$
. Hence, up to a reorder of the
$i_k\ne i_l$
. Hence, up to a reorder of the
![]() $\gamma _j$
’s, we may and do assume, without loss of generality,
$\gamma _j$
’s, we may and do assume, without loss of generality,
![]() $i_k=k$
, for every
$i_k=k$
, for every
![]() $k\in \{1,\dots ,s\}$
, i.e.
$k\in \{1,\dots ,s\}$
, i.e.
 $$ \begin{align} \lambda_{ki}=\begin{cases}-\frac12 c_{ki}, \quad &\mbox {if } i\ne k, \\ -\frac12 c_{kk}-\frac{\sqrt{-1}}{4},\quad & \mbox{if } i=k.\end{cases} \end{align} $$
$$ \begin{align} \lambda_{ki}=\begin{cases}-\frac12 c_{ki}, \quad &\mbox {if } i\ne k, \\ -\frac12 c_{kk}-\frac{\sqrt{-1}}{4},\quad & \mbox{if } i=k.\end{cases} \end{align} $$
Proposition 5.2 (Characterization of left-invariant pluriclosed metrics on Oeljeklaus–Toma manifolds).
A left-invariant metric
![]() $\omega $
on an Oeljeklaus–Toma manifold admitting pluriclosed metrics is pluriclosed if and only if it takes the following expression with respect to a coframe
$\omega $
on an Oeljeklaus–Toma manifold admitting pluriclosed metrics is pluriclosed if and only if it takes the following expression with respect to a coframe
![]() $\{\omega ^1,\dots ,\omega ^s,\gamma ^1,\dots ,\gamma ^s\}$
satisfying (
1
) and (
15
):
$\{\omega ^1,\dots ,\omega ^s,\gamma ^1,\dots ,\gamma ^s\}$
satisfying (
1
) and (
15
):
 $$ \begin{align} \omega=\sqrt{-1}\sum_{i=1}^sA_i\omega^i\wedge \bar \omega^i+ B_i\gamma^i\wedge \bar \gamma^i+ \sqrt{-1}\sum_{r=1}^{k}\left( C_{r}\omega^{p_r}\wedge \bar \gamma^{p_r}+\bar C_{r}\gamma^{p_r}\wedge\bar \omega^{p_r} \right) \end{align} $$
$$ \begin{align} \omega=\sqrt{-1}\sum_{i=1}^sA_i\omega^i\wedge \bar \omega^i+ B_i\gamma^i\wedge \bar \gamma^i+ \sqrt{-1}\sum_{r=1}^{k}\left( C_{r}\omega^{p_r}\wedge \bar \gamma^{p_r}+\bar C_{r}\gamma^{p_r}\wedge\bar \omega^{p_r} \right) \end{align} $$
for some
![]() $A_1,\dots ,A_s,B_1,\dots ,B_s\in \mathbb R_+$
,
$A_1,\dots ,A_s,B_1,\dots ,B_s\in \mathbb R_+$
,
![]() $C_1,\dots ,C_k\in \mathbb C$
, where
$C_1,\dots ,C_k\in \mathbb C$
, where
![]() $\{p_1,\dots ,p_k\}\subseteq \{1,\dots ,s\}$
are such that
$\{p_1,\dots ,p_k\}\subseteq \{1,\dots ,s\}$
are such that
Proof We assume
![]() $s>1$
since the case
$s>1$
since the case
![]() $s=1$
is trivial. Let
$s=1$
is trivial. Let
 $$\begin{align*}\omega=\sqrt{-1}\sum_{p,q=1}^sA_{p\bar q}\omega^p\wedge\bar{\omega}^q+B_{p\bar q}\gamma^p\wedge\bar{\gamma}^q+C_{p\bar q}\omega^p\wedge\bar{\gamma}^q+\bar C_{ p\bar q} \gamma^q\wedge \bar{\omega}^p\end{align*}$$
$$\begin{align*}\omega=\sqrt{-1}\sum_{p,q=1}^sA_{p\bar q}\omega^p\wedge\bar{\omega}^q+B_{p\bar q}\gamma^p\wedge\bar{\gamma}^q+C_{p\bar q}\omega^p\wedge\bar{\gamma}^q+\bar C_{ p\bar q} \gamma^q\wedge \bar{\omega}^p\end{align*}$$
be an arbitrary real left-invariant
![]() $(1,1)$
-form on M, with
$(1,1)$
-form on M, with
![]() $A_{p\bar p}, B_{p\bar p}\in {\mathbb R}$
, for every
$A_{p\bar p}, B_{p\bar p}\in {\mathbb R}$
, for every
![]() ${p=1,\ldots , s}$
,
${p=1,\ldots , s}$
,
![]() $A_{p\bar q}, B_{p\bar q}\in {\mathbb C}$
, for all
$A_{p\bar q}, B_{p\bar q}\in {\mathbb C}$
, for all
![]() $p,q=1,\ldots , s$
with
$p,q=1,\ldots , s$
with
![]() $ p\ne q$
, and
$ p\ne q$
, and
![]() $ C_{p\bar q}\in {\mathbb C}$
, for every
$ C_{p\bar q}\in {\mathbb C}$
, for every
![]() ${p,q=1,\ldots , s}$
.
${p,q=1,\ldots , s}$
.
From the structure equations (1), it easily follows
 $$ \begin{align} \begin{cases} & \partial\bar\partial(\omega^p\wedge\bar\omega^q)\in \langle \omega^{p}\wedge \omega^q\wedge \bar \omega^p\wedge \bar\omega ^q \rangle, \\ & \partial\bar\partial(\omega^p\wedge\bar\gamma^q)\in \langle \omega^{i}\wedge \omega^j\wedge \bar \omega^l\wedge \bar\gamma^m\rangle, \\ & \partial\bar\partial(\gamma^p\wedge\bar\gamma^q)\in \langle \omega^{i}\wedge\bar \omega^j\wedge\gamma^l\wedge \bar\gamma^m\rangle, \\ \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} & \partial\bar\partial(\omega^p\wedge\bar\omega^q)\in \langle \omega^{p}\wedge \omega^q\wedge \bar \omega^p\wedge \bar\omega ^q \rangle, \\ & \partial\bar\partial(\omega^p\wedge\bar\gamma^q)\in \langle \omega^{i}\wedge \omega^j\wedge \bar \omega^l\wedge \bar\gamma^m\rangle, \\ & \partial\bar\partial(\gamma^p\wedge\bar\gamma^q)\in \langle \omega^{i}\wedge\bar \omega^j\wedge\gamma^l\wedge \bar\gamma^m\rangle, \\ \end{cases} \end{align} $$
and that
![]() $\omega $
is pluriclosed if and only if the following three conditions are satisfied:
$\omega $
is pluriclosed if and only if the following three conditions are satisfied:
 $$ \begin{align} && \sum_{p,q=1}^sA_{p\bar q}\partial\bar{\partial}(\omega^p\wedge\bar{\omega}^q)=0 , \end{align} $$
$$ \begin{align} && \sum_{p,q=1}^sA_{p\bar q}\partial\bar{\partial}(\omega^p\wedge\bar{\omega}^q)=0 , \end{align} $$
 $$ \begin{align} && \sum_{p,q=1}^sB_{p\bar q}\partial\bar{\partial}(\gamma^p\wedge\bar{\gamma}^q)=0 , \end{align} $$
$$ \begin{align} && \sum_{p,q=1}^sB_{p\bar q}\partial\bar{\partial}(\gamma^p\wedge\bar{\gamma}^q)=0 , \end{align} $$
 $$ \begin{align} && \sum_{p,q=1}^sC_{p\bar q}\partial\bar{\partial}(\omega^p\wedge\bar{\gamma}^q)=0 . \end{align} $$
$$ \begin{align} && \sum_{p,q=1}^sC_{p\bar q}\partial\bar{\partial}(\omega^p\wedge\bar{\gamma}^q)=0 . \end{align} $$
The first relation in (17) yields that (18) is satisfied if and only if
Next, we focus on (19). We have
 $$ \begin{align*}\begin{aligned} \partial\bar\partial(\gamma^p\wedge\bar{\gamma}^q)=& \partial\left(-\sum_{\delta=1}^s\lambda_{\delta p}\bar{\omega}^{\delta}\wedge\gamma^p\wedge\bar{\gamma}^q-\gamma^p\wedge\sum_{\delta=1}^s\bar\lambda_{\delta q}\bar{\omega}^{\delta}\wedge\bar{\gamma}^q\right)\, \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \partial\bar\partial(\gamma^p\wedge\bar{\gamma}^q)=& \partial\left(-\sum_{\delta=1}^s\lambda_{\delta p}\bar{\omega}^{\delta}\wedge\gamma^p\wedge\bar{\gamma}^q-\gamma^p\wedge\sum_{\delta=1}^s\bar\lambda_{\delta q}\bar{\omega}^{\delta}\wedge\bar{\gamma}^q\right)\, \end{aligned} \end{align*} $$
and
 $$ \begin{align*}\begin{aligned} \partial\bar\partial(\gamma^p\wedge\bar{\gamma}^q)=&\, \sum_{\delta=1}^s(\bar\lambda_{\delta q}-\lambda_{\delta p})\left(\partial\bar{\omega}^{\delta}\wedge\gamma^p\wedge\bar{\gamma}^q-\bar{\omega}^{\delta}\wedge\partial\gamma^p\wedge\bar{\gamma}^q+\bar{\omega}^{\delta}\wedge \gamma^p\wedge \partial\bar{\gamma}^q\right), \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \partial\bar\partial(\gamma^p\wedge\bar{\gamma}^q)=&\, \sum_{\delta=1}^s(\bar\lambda_{\delta q}-\lambda_{\delta p})\left(\partial\bar{\omega}^{\delta}\wedge\gamma^p\wedge\bar{\gamma}^q-\bar{\omega}^{\delta}\wedge\partial\gamma^p\wedge\bar{\gamma}^q+\bar{\omega}^{\delta}\wedge \gamma^p\wedge \partial\bar{\gamma}^q\right), \end{aligned} \end{align*} $$
which implies that
 $$ \begin{align*}\begin{aligned} \partial\bar\partial(\gamma^p\wedge\bar{\gamma}^q)=&\, \sum_{\delta=1}^s\frac{\sqrt{-1}}{2}(\bar\lambda_{\delta q}-\lambda_{\delta p})\omega^{\delta}\wedge\bar{\omega}^{\delta}\wedge\gamma^p\wedge\bar{\gamma}^q-\sum_{\delta=1}^s(\bar\lambda_{\delta q}-\lambda_{\delta p})\bar{\omega}^{\delta}\wedge\left(\sum_{a=1}^s\lambda_{ap}\omega^a\wedge\gamma^p\right)\wedge\bar{\gamma}^q\\ &\,+\sum_{\delta=1}^s(\bar\lambda_{\delta q}-\lambda_{\delta p})\bar{\omega}^{\delta}\wedge\gamma^{p}\wedge\left(-\sum_{a=1}^s\bar\lambda_{aq}\omega^a\wedge\bar{\gamma}^q\right)\\ =&\sum_{\delta=1}^s\frac{\sqrt{-1}}{2}(\bar\lambda_{\delta q}-\lambda_{\delta p})\omega^{\delta}\wedge\bar{\omega}^{\delta}\wedge{\gamma^p}\wedge\bar{\gamma}^q+\sum_{\delta, a}(\lambda_{ap}-\bar\lambda_{aq})(\bar\lambda_{\delta q}-\lambda_{\delta p})\omega^a\wedge\bar{\omega}^{\delta}\kern1.2pt{\wedge}\kern1.2pt\gamma^p\wedge\bar{\gamma}^q. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \partial\bar\partial(\gamma^p\wedge\bar{\gamma}^q)=&\, \sum_{\delta=1}^s\frac{\sqrt{-1}}{2}(\bar\lambda_{\delta q}-\lambda_{\delta p})\omega^{\delta}\wedge\bar{\omega}^{\delta}\wedge\gamma^p\wedge\bar{\gamma}^q-\sum_{\delta=1}^s(\bar\lambda_{\delta q}-\lambda_{\delta p})\bar{\omega}^{\delta}\wedge\left(\sum_{a=1}^s\lambda_{ap}\omega^a\wedge\gamma^p\right)\wedge\bar{\gamma}^q\\ &\,+\sum_{\delta=1}^s(\bar\lambda_{\delta q}-\lambda_{\delta p})\bar{\omega}^{\delta}\wedge\gamma^{p}\wedge\left(-\sum_{a=1}^s\bar\lambda_{aq}\omega^a\wedge\bar{\gamma}^q\right)\\ =&\sum_{\delta=1}^s\frac{\sqrt{-1}}{2}(\bar\lambda_{\delta q}-\lambda_{\delta p})\omega^{\delta}\wedge\bar{\omega}^{\delta}\wedge{\gamma^p}\wedge\bar{\gamma}^q+\sum_{\delta, a}(\lambda_{ap}-\bar\lambda_{aq})(\bar\lambda_{\delta q}-\lambda_{\delta p})\omega^a\wedge\bar{\omega}^{\delta}\kern1.2pt{\wedge}\kern1.2pt\gamma^p\wedge\bar{\gamma}^q. \end{aligned} \end{align*} $$
Finally, we get
 $$ \begin{align*} \partial\bar\partial(\gamma^p\wedge\bar{\gamma}^q)=\sum_{\delta=1}^s(\bar\lambda_{\delta q}-\lambda_{\delta p})\left(\frac{\sqrt{-1}}{2}+\lambda_{\delta p}-\bar\lambda_{\delta q}\right)\omega^{\delta}\wedge\bar{\omega}^{\delta}\wedge{\gamma^p}\wedge\bar{\gamma}^q\\+\sum_{\delta\ne a}(\lambda_{ap} -\bar\lambda_{aq})(\bar\lambda_{\delta q}-\lambda_{\delta p})\omega^a\wedge\bar{\omega}^{\delta}\wedge\gamma^p\wedge\bar{\gamma}^q \end{align*} $$
$$ \begin{align*} \partial\bar\partial(\gamma^p\wedge\bar{\gamma}^q)=\sum_{\delta=1}^s(\bar\lambda_{\delta q}-\lambda_{\delta p})\left(\frac{\sqrt{-1}}{2}+\lambda_{\delta p}-\bar\lambda_{\delta q}\right)\omega^{\delta}\wedge\bar{\omega}^{\delta}\wedge{\gamma^p}\wedge\bar{\gamma}^q\\+\sum_{\delta\ne a}(\lambda_{ap} -\bar\lambda_{aq})(\bar\lambda_{\delta q}-\lambda_{\delta p})\omega^a\wedge\bar{\omega}^{\delta}\wedge\gamma^p\wedge\bar{\gamma}^q \end{align*} $$
and that condition (19) is equivalent to
 $$ \begin{align*} B_{p\bar q}\left(\sum_{\delta=1}^s(\bar\lambda_{\delta q}-\lambda_{\delta p})\left(\frac{\sqrt{-1}}{2} +\lambda_{\delta p}-\bar\lambda_{\delta q}\right)\omega^{\delta}\wedge\bar{\omega}^{\delta} +\sum_{\delta\ne a}(\lambda_{ap}-\bar\lambda_{aq})(\bar\lambda_{\delta q}-\lambda_{\delta p})\omega^a\wedge\bar{\omega}^{\delta}\right)=0, \end{align*} $$
$$ \begin{align*} B_{p\bar q}\left(\sum_{\delta=1}^s(\bar\lambda_{\delta q}-\lambda_{\delta p})\left(\frac{\sqrt{-1}}{2} +\lambda_{\delta p}-\bar\lambda_{\delta q}\right)\omega^{\delta}\wedge\bar{\omega}^{\delta} +\sum_{\delta\ne a}(\lambda_{ap}-\bar\lambda_{aq})(\bar\lambda_{\delta q}-\lambda_{\delta p})\omega^a\wedge\bar{\omega}^{\delta}\right)=0, \end{align*} $$
for every
![]() $p,q=1,\dots , s.$
$p,q=1,\dots , s.$
By using our conditions on the
![]() $b_{ki}$
’s, it is easy to show that the quantity
$b_{ki}$
’s, it is easy to show that the quantity
 $$ \begin{align*}\sum_{\delta=1}^s(\bar\lambda_{\delta q}-\lambda_{\delta p})\left(\frac{\sqrt{-1}}{2} +\lambda_{\delta p}-\bar\lambda_{\delta q}\right)\omega^{\delta}\wedge\bar{\omega}^{\delta} +\sum_{\delta\ne a}(\lambda_{ap}-\bar\lambda_{aq})(\bar\lambda_{\delta q}-\lambda_{\delta p})\omega^a\wedge\bar{\omega}^{\delta} \end{align*} $$
$$ \begin{align*}\sum_{\delta=1}^s(\bar\lambda_{\delta q}-\lambda_{\delta p})\left(\frac{\sqrt{-1}}{2} +\lambda_{\delta p}-\bar\lambda_{\delta q}\right)\omega^{\delta}\wedge\bar{\omega}^{\delta} +\sum_{\delta\ne a}(\lambda_{ap}-\bar\lambda_{aq})(\bar\lambda_{\delta q}-\lambda_{\delta p})\omega^a\wedge\bar{\omega}^{\delta} \end{align*} $$
is vanishing for
![]() $p=q$
and, consequently, there are no restrictions on the
$p=q$
and, consequently, there are no restrictions on the
![]() $B_{q\bar q}$
’s. Now, we observe that the real part of
$B_{q\bar q}$
’s. Now, we observe that the real part of
 $$ \begin{align*}(\bar\lambda_{p q}-\lambda_{p p})\left(\frac{\sqrt{-1}}{2} +\lambda_{p p}-\bar\lambda_{p q}\right) \end{align*} $$
$$ \begin{align*}(\bar\lambda_{p q}-\lambda_{p p})\left(\frac{\sqrt{-1}}{2} +\lambda_{p p}-\bar\lambda_{p q}\right) \end{align*} $$
is different from
![]() $0$
, for every
$0$
, for every
![]() $p,q$
with
$p,q$
with
![]() $p\neq q$
, which forces
$p\neq q$
, which forces
![]() $B_{p\bar q}=0$
, for
$B_{p\bar q}=0$
, for
![]() $p\neq q$
. Indeed, we have
$p\neq q$
. Indeed, we have
 $$ \begin{align*} &\bar \lambda_{\delta q}-\lambda_{\delta p}=\frac12 (c_{\delta p}-c_{\delta q})-\frac{\sqrt{-1}}{4}(b_{\delta p}+b_{\delta q}), \\ & \frac{\sqrt{-1}}{2}+\lambda_{\delta p}-\bar\lambda_{\delta q}=-\frac12(c_{\delta p}-c_{\delta q})+\frac{\sqrt{-1}}{2}\left(1+\frac{b_{\delta p}+b_{\delta q}}{2}\right), \end{align*} $$
$$ \begin{align*} &\bar \lambda_{\delta q}-\lambda_{\delta p}=\frac12 (c_{\delta p}-c_{\delta q})-\frac{\sqrt{-1}}{4}(b_{\delta p}+b_{\delta q}), \\ & \frac{\sqrt{-1}}{2}+\lambda_{\delta p}-\bar\lambda_{\delta q}=-\frac12(c_{\delta p}-c_{\delta q})+\frac{\sqrt{-1}}{2}\left(1+\frac{b_{\delta p}+b_{\delta q}}{2}\right), \end{align*} $$
which implies that
 $$ \begin{align} &\Re\mathfrak e\,\left((\bar \lambda_{\delta q}-\lambda_{\delta p})\left(\frac{\sqrt{-1}}{2}+\lambda_{\delta q}-\bar \lambda_{\delta p}\right)\right)\\&\quad=-\frac{(c_{\delta p}-c_{\delta q})^2}{4}+\frac14\left(\frac{b_{\delta p}+b_{\delta q}}{2}\right)\left(1+\frac{b_{\delta p}+b_{\delta q}}{2}\right).\nonumber \end{align} $$
$$ \begin{align} &\Re\mathfrak e\,\left((\bar \lambda_{\delta q}-\lambda_{\delta p})\left(\frac{\sqrt{-1}}{2}+\lambda_{\delta q}-\bar \lambda_{\delta p}\right)\right)\\&\quad=-\frac{(c_{\delta p}-c_{\delta q})^2}{4}+\frac14\left(\frac{b_{\delta p}+b_{\delta q}}{2}\right)\left(1+\frac{b_{\delta p}+b_{\delta q}}{2}\right).\nonumber \end{align} $$
Since
![]() $p\ne q$
, we have
$p\ne q$
, we have
and so (21) computed for
![]() $\delta =q$
gives
$\delta =q$
gives
 $$ \begin{align*}\Re\mathfrak e\left(\left(\bar \lambda_{p q}-\lambda_{p p}\right)\left(\frac{\sqrt{-1}}{2}+\lambda_{p q}-\bar \lambda_{p p})\right)\right)=\frac14\left( -(c_{p p}-c_{p q})^2-\frac14\right)\ne 0, \end{align*} $$
$$ \begin{align*}\Re\mathfrak e\left(\left(\bar \lambda_{p q}-\lambda_{p p}\right)\left(\frac{\sqrt{-1}}{2}+\lambda_{p q}-\bar \lambda_{p p})\right)\right)=\frac14\left( -(c_{p p}-c_{p q})^2-\frac14\right)\ne 0, \end{align*} $$
as required. Therefore, equation (19) is satisfied if and only if
Next, we focus on (20). We have
 $$ \begin{align*}\begin{aligned} \partial\bar{\partial}(\omega^p\wedge\bar{\gamma}^q)=&\, \partial\left(\frac{\sqrt{-1}}{2}\omega^p\wedge\bar{\omega}^p\wedge\bar{\gamma}^q-\omega^p\wedge\left(\sum_{\delta=1}^s\bar \lambda_{\delta q}\bar{\omega}^{\delta}\wedge \bar{\gamma}^q\right)\right)\\ \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \partial\bar{\partial}(\omega^p\wedge\bar{\gamma}^q)=&\, \partial\left(\frac{\sqrt{-1}}{2}\omega^p\wedge\bar{\omega}^p\wedge\bar{\gamma}^q-\omega^p\wedge\left(\sum_{\delta=1}^s\bar \lambda_{\delta q}\bar{\omega}^{\delta}\wedge \bar{\gamma}^q\right)\right)\\ \end{aligned} \end{align*} $$
and
 $$ \begin{align*}\begin{aligned} \partial\bar{\partial}(\omega^p\wedge\bar{\gamma}^q)=&\, \frac{\sqrt{-1}}{2}\left(-\frac{\sqrt{-1}}{2}\omega^p\wedge\omega^p\wedge\bar{\omega}^p\wedge\bar{\gamma}^q+\omega^p\wedge\bar{\omega}^p\wedge\left(-\sum_{\delta=1}^s\bar {\lambda}_{\delta q}\omega^{\delta}\wedge\bar{\gamma}^q\right)\right)\\ &\,+\sum_{\delta=1}^s\frac{\sqrt{-1}}{2}\bar \lambda_{\delta q}\omega^p\wedge\omega^{\delta}\wedge\bar{\omega}^{\delta}\wedge\bar{\gamma}^q+\sum_{\delta=1}^s\bar \lambda_{\delta q}\omega^p\wedge\bar{\omega}^{\delta}\kern1pt{\wedge}\kern1pt\left(\sum_{a=1}^s\bar \lambda_{aq}\omega^a\kern1pt{\wedge}\kern1pt\bar{\gamma}^q\right). \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \partial\bar{\partial}(\omega^p\wedge\bar{\gamma}^q)=&\, \frac{\sqrt{-1}}{2}\left(-\frac{\sqrt{-1}}{2}\omega^p\wedge\omega^p\wedge\bar{\omega}^p\wedge\bar{\gamma}^q+\omega^p\wedge\bar{\omega}^p\wedge\left(-\sum_{\delta=1}^s\bar {\lambda}_{\delta q}\omega^{\delta}\wedge\bar{\gamma}^q\right)\right)\\ &\,+\sum_{\delta=1}^s\frac{\sqrt{-1}}{2}\bar \lambda_{\delta q}\omega^p\wedge\omega^{\delta}\wedge\bar{\omega}^{\delta}\wedge\bar{\gamma}^q+\sum_{\delta=1}^s\bar \lambda_{\delta q}\omega^p\wedge\bar{\omega}^{\delta}\kern1pt{\wedge}\kern1pt\left(\sum_{a=1}^s\bar \lambda_{aq}\omega^a\kern1pt{\wedge}\kern1pt\bar{\gamma}^q\right). \end{aligned} \end{align*} $$
Hence, we get
 $$ \begin{align*} \partial\bar{\partial}(\omega^p\wedge\bar{\gamma}^q)&= \sum_{\substack{\delta=1\\ \delta\ne p}}^s\frac{\sqrt{-1}}{2}\bar\lambda_{\delta q}\omega^p\wedge\bar{\omega}^p\wedge\omega^{\delta}\wedge\bar\gamma^q+\sum_{\substack{\delta=1\\ \delta\ne p}}^s\frac{\sqrt{-1}}{2}\bar \lambda_{\delta q}\omega^p\wedge\omega^{\delta}\wedge\bar{\omega}^{\delta}\wedge\bar{\gamma}^q\\ &\quad+\sum_{\substack{\delta, a \\ a\ne p}}\bar \lambda_{\delta q}\bar \lambda_{aq}\omega^p\wedge\bar{\omega}^{\delta}\wedge\omega^a\wedge\bar{\gamma}^q \end{align*} $$
$$ \begin{align*} \partial\bar{\partial}(\omega^p\wedge\bar{\gamma}^q)&= \sum_{\substack{\delta=1\\ \delta\ne p}}^s\frac{\sqrt{-1}}{2}\bar\lambda_{\delta q}\omega^p\wedge\bar{\omega}^p\wedge\omega^{\delta}\wedge\bar\gamma^q+\sum_{\substack{\delta=1\\ \delta\ne p}}^s\frac{\sqrt{-1}}{2}\bar \lambda_{\delta q}\omega^p\wedge\omega^{\delta}\wedge\bar{\omega}^{\delta}\wedge\bar{\gamma}^q\\ &\quad+\sum_{\substack{\delta, a \\ a\ne p}}\bar \lambda_{\delta q}\bar \lambda_{aq}\omega^p\wedge\bar{\omega}^{\delta}\wedge\omega^a\wedge\bar{\gamma}^q \end{align*} $$
and
 $$ \begin{align*} \partial\bar{\partial}(\omega^p\wedge\bar{\gamma}^q)&=\sum_{\substack{\delta=1\\ \delta\ne p}}^s\frac{\sqrt{-1}}{2}\bar\lambda_{\delta q}\omega^p\wedge\bar{\omega}^p\wedge\omega^{\delta}\wedge\bar\gamma^q+\sum_{\substack{a=1\\ a\ne p }}^s\bar\lambda_{pq}\bar\lambda_{aq}\omega^p\wedge\bar{\omega}^{p}\wedge\omega^a\wedge\bar{\gamma}^q\\&\quad+\sum_{\substack{\delta=1\\ \delta\ne p}}^s\frac{\sqrt{-1}}{2}\bar\lambda_{\delta q}\omega^p\wedge\omega^{\delta}\wedge\bar{\omega}^{\delta}\wedge\bar{\gamma}^q+\sum_{\substack{\delta, a \\ \delta\ne p \\ a\ne p}}\bar\lambda_{\delta q}\bar\lambda_{aq}\omega^p\wedge\bar{\omega}^{\delta}\wedge\omega^a\wedge\bar{\gamma}^q. \end{align*} $$
$$ \begin{align*} \partial\bar{\partial}(\omega^p\wedge\bar{\gamma}^q)&=\sum_{\substack{\delta=1\\ \delta\ne p}}^s\frac{\sqrt{-1}}{2}\bar\lambda_{\delta q}\omega^p\wedge\bar{\omega}^p\wedge\omega^{\delta}\wedge\bar\gamma^q+\sum_{\substack{a=1\\ a\ne p }}^s\bar\lambda_{pq}\bar\lambda_{aq}\omega^p\wedge\bar{\omega}^{p}\wedge\omega^a\wedge\bar{\gamma}^q\\&\quad+\sum_{\substack{\delta=1\\ \delta\ne p}}^s\frac{\sqrt{-1}}{2}\bar\lambda_{\delta q}\omega^p\wedge\omega^{\delta}\wedge\bar{\omega}^{\delta}\wedge\bar{\gamma}^q+\sum_{\substack{\delta, a \\ \delta\ne p \\ a\ne p}}\bar\lambda_{\delta q}\bar\lambda_{aq}\omega^p\wedge\bar{\omega}^{\delta}\wedge\omega^a\wedge\bar{\gamma}^q. \end{align*} $$
Therefore,
 $$ \begin{align*} &\partial\bar{\partial}(\omega^p\wedge\bar{\gamma}^q)=\sum_{\substack{\delta=1\\ \delta\ne p}}^s\bar\lambda_{\delta q}\left(\frac{\sqrt{-1}}{2}+\bar\lambda_{pq}\right)\omega^p\wedge\bar{\omega}^p\wedge\omega^{\delta}\wedge\bar\gamma^q\\ &\quad+\sum_{\substack{\delta=1\\ \delta\ne p}}^s\bar\lambda_{\delta q}\left(\frac{\sqrt{-1}}{2}-\bar\lambda_{\delta q}\right)\omega^p\wedge\omega^{\delta}\wedge\bar{\omega}^{\delta}\wedge\bar{\gamma}^q+\sum_{\substack{\delta\ne a \\ \delta\ne p \\ a\ne p}}\bar\lambda_{\delta q}\bar\lambda_{aq}\omega^p\wedge\bar{\omega}^{\delta}\wedge\omega^a\wedge\bar{\gamma}^q \end{align*} $$
$$ \begin{align*} &\partial\bar{\partial}(\omega^p\wedge\bar{\gamma}^q)=\sum_{\substack{\delta=1\\ \delta\ne p}}^s\bar\lambda_{\delta q}\left(\frac{\sqrt{-1}}{2}+\bar\lambda_{pq}\right)\omega^p\wedge\bar{\omega}^p\wedge\omega^{\delta}\wedge\bar\gamma^q\\ &\quad+\sum_{\substack{\delta=1\\ \delta\ne p}}^s\bar\lambda_{\delta q}\left(\frac{\sqrt{-1}}{2}-\bar\lambda_{\delta q}\right)\omega^p\wedge\omega^{\delta}\wedge\bar{\omega}^{\delta}\wedge\bar{\gamma}^q+\sum_{\substack{\delta\ne a \\ \delta\ne p \\ a\ne p}}\bar\lambda_{\delta q}\bar\lambda_{aq}\omega^p\wedge\bar{\omega}^{\delta}\wedge\omega^a\wedge\bar{\gamma}^q \end{align*} $$
and (20) is equivalent to
 $$ \begin{align*}C_{p\bar{q}}\left(\sum_{\substack{\delta=1\\ \delta\ne p}}^s\bar\lambda_{\delta q}\left(\frac{\sqrt{-1}}{2}+\bar\lambda_{pq}\right)\bar{\omega}^p\wedge\omega^{\delta} +\sum_{\substack{\delta=1\\ \delta\ne p}}^s\bar\lambda_{\delta q}\left(\frac{\sqrt{-1}}{2}-\bar\lambda_{\delta q}\right)\omega^{\delta}\wedge\bar{\omega}^{\delta} +\sum_{\substack{\delta\ne a \\ \delta\ne p \\ a\ne p}}\bar\lambda_{\delta q}\bar\lambda_{aq}\bar{\omega}^{\delta}\wedge\omega^a\right)=0, \end{align*} $$
$$ \begin{align*}C_{p\bar{q}}\left(\sum_{\substack{\delta=1\\ \delta\ne p}}^s\bar\lambda_{\delta q}\left(\frac{\sqrt{-1}}{2}+\bar\lambda_{pq}\right)\bar{\omega}^p\wedge\omega^{\delta} +\sum_{\substack{\delta=1\\ \delta\ne p}}^s\bar\lambda_{\delta q}\left(\frac{\sqrt{-1}}{2}-\bar\lambda_{\delta q}\right)\omega^{\delta}\wedge\bar{\omega}^{\delta} +\sum_{\substack{\delta\ne a \\ \delta\ne p \\ a\ne p}}\bar\lambda_{\delta q}\bar\lambda_{aq}\bar{\omega}^{\delta}\wedge\omega^a\right)=0, \end{align*} $$
for every
![]() $p,q=1,\dots ,s$
. Since
$p,q=1,\dots ,s$
. Since
the quantity
 $$ \begin{align*}E_{p\bar q}:=\sum_{\substack{\delta=1\\ \delta\ne p}}^s\bar\lambda_{\delta q}\left(\frac{\sqrt{-1}}{2}+\bar\lambda_{pq}\right)\bar{\omega}^p\wedge\omega^{\delta} +\sum_{\substack{\delta=1\\ \delta\ne p}}^s\bar\lambda_{\delta q}\left(\frac{\sqrt{-1}}{2}-\bar\lambda_{\delta q}\right)\omega^{\delta}\wedge\bar{\omega}^{\delta} +\sum_{\substack{\delta\ne a \\ \delta\ne p \\ a\ne p}}\bar\lambda_{\delta q}\bar\lambda_{aq}\bar{\omega}^{\delta}\wedge\omega^a \end{align*} $$
$$ \begin{align*}E_{p\bar q}:=\sum_{\substack{\delta=1\\ \delta\ne p}}^s\bar\lambda_{\delta q}\left(\frac{\sqrt{-1}}{2}+\bar\lambda_{pq}\right)\bar{\omega}^p\wedge\omega^{\delta} +\sum_{\substack{\delta=1\\ \delta\ne p}}^s\bar\lambda_{\delta q}\left(\frac{\sqrt{-1}}{2}-\bar\lambda_{\delta q}\right)\omega^{\delta}\wedge\bar{\omega}^{\delta} +\sum_{\substack{\delta\ne a \\ \delta\ne p \\ a\ne p}}\bar\lambda_{\delta q}\bar\lambda_{aq}\bar{\omega}^{\delta}\wedge\omega^a \end{align*} $$
is vanishing if and only if
Since
![]() $\lambda _{qq}\neq 0$
, it follows
$\lambda _{qq}\neq 0$
, it follows
and
Hence, the claim follows.
Proposition 5.3 Let
 $$ \begin{align} \omega=\sqrt{-1}\sum_{i=1}^sA_i\omega^i\wedge \bar \omega^i+ B_i\gamma^i\wedge \bar \gamma^i+ \sqrt{-1}\sum_{r=1}^{k}\left( C_{r}\omega^{p_r}\wedge \bar \gamma^{p_r}+\bar C_{r}\gamma^{p_r}\wedge \bar \omega^{p_r} \right) \end{align} $$
$$ \begin{align} \omega=\sqrt{-1}\sum_{i=1}^sA_i\omega^i\wedge \bar \omega^i+ B_i\gamma^i\wedge \bar \gamma^i+ \sqrt{-1}\sum_{r=1}^{k}\left( C_{r}\omega^{p_r}\wedge \bar \gamma^{p_r}+\bar C_{r}\gamma^{p_r}\wedge \bar \omega^{p_r} \right) \end{align} $$
be a left-invariant pluriclosed Hermitian metric on an Oeljeklaus–Toma manifold, where the components are with respect to a coframe
![]() $\{\omega ^1,\dots ,\omega ^s,\gamma ^1,\dots ,\gamma ^s\}$
satisfying (1) and (15) and
$\{\omega ^1,\dots ,\omega ^s,\gamma ^1,\dots ,\gamma ^s\}$
satisfying (1) and (15) and
![]() $\{p_1,\dots ,p_k\}\subseteq \{1,\dots ,s\}$
are such that
$\{p_1,\dots ,p_k\}\subseteq \{1,\dots ,s\}$
are such that
Then the
![]() $(1,1)$
-part of the Bismut–Ricci form of
$(1,1)$
-part of the Bismut–Ricci form of
![]() $\omega $
takes the following expression:
$\omega $
takes the following expression:
 $$ \begin{align*}\rho^{1,1}_B=-\sqrt{-1}\sum_{r=1}^k\frac{3}{4}\left(1+\frac{\lvert C_{r}\rvert^2}{A_{p_r}B_{p_r}-\lvert C_{r}\rvert^2}\right)\omega^{p_r}\wedge \bar \omega^{p_r}-\sqrt{-1}\sum_{i\not\in\{p_1,\ldots, p_k\}} \frac{3}{4}\omega^i\wedge\bar{\omega}^i \end{align*} $$
$$ \begin{align*}\rho^{1,1}_B=-\sqrt{-1}\sum_{r=1}^k\frac{3}{4}\left(1+\frac{\lvert C_{r}\rvert^2}{A_{p_r}B_{p_r}-\lvert C_{r}\rvert^2}\right)\omega^{p_r}\wedge \bar \omega^{p_r}-\sqrt{-1}\sum_{i\not\in\{p_1,\ldots, p_k\}} \frac{3}{4}\omega^i\wedge\bar{\omega}^i \end{align*} $$
 $$ \begin{align*}-\sqrt{-1}\sum_{r=1}^k\left(-\frac{3}{16}-\frac{c_{p_rp_r}^2}{4}-\frac{\sqrt{-1}c_{p_rp_r}}{4}\right)\frac{B_{p_r}C_r}{A_{p_r}B_{p_r}-|C_r|^2}\omega^{p_r}\wedge \bar \gamma^{p_r} + \quad {\textit{conjugates}}. \end{align*} $$
$$ \begin{align*}-\sqrt{-1}\sum_{r=1}^k\left(-\frac{3}{16}-\frac{c_{p_rp_r}^2}{4}-\frac{\sqrt{-1}c_{p_rp_r}}{4}\right)\frac{B_{p_r}C_r}{A_{p_r}B_{p_r}-|C_r|^2}\omega^{p_r}\wedge \bar \gamma^{p_r} + \quad {\textit{conjugates}}. \end{align*} $$
Proof We recall that the Bismut–Ricci form of a left-invariant Hermitian metric
![]() $\omega =\sqrt {-1}\sum _{a,b=1}^n g_{a\bar b}\alpha ^a\wedge \bar \alpha ^b $
on a Lie group
$\omega =\sqrt {-1}\sum _{a,b=1}^n g_{a\bar b}\alpha ^a\wedge \bar \alpha ^b $
on a Lie group
![]() $G^{2n}$
with a left-invariant complex structure takes the following algebraic expression:
$G^{2n}$
with a left-invariant complex structure takes the following algebraic expression:
 $$ \begin{align} \rho_B(X, Y)=&-\sum_{a,b=1}^{n}g^{a\bar b}\omega([[X,Y]^{1,0}, X_a], \bar{X_b})+ g^{\bar a b }\omega([[X,Y]^{0,1},\bar{X_a}], X_b)\\&+\sqrt{-1} \sum_{a,b=1}^ng^{a\bar b}\omega([X,Y],J[X_a,\bar{X_b}])\, , \nonumber\end{align} $$
$$ \begin{align} \rho_B(X, Y)=&-\sum_{a,b=1}^{n}g^{a\bar b}\omega([[X,Y]^{1,0}, X_a], \bar{X_b})+ g^{\bar a b }\omega([[X,Y]^{0,1},\bar{X_a}], X_b)\\&+\sqrt{-1} \sum_{a,b=1}^ng^{a\bar b}\omega([X,Y],J[X_a,\bar{X_b}])\, , \nonumber\end{align} $$
for every left-invariant vector fields
![]() $X,Y$
on G, where
$X,Y$
on G, where
![]() $\{\alpha ^i\}$
is a left-invariant
$\{\alpha ^i\}$
is a left-invariant
![]() $(1,0)$
-coframe with dual frame
$(1,0)$
-coframe with dual frame
![]() $\{X_a\}$
and
$\{X_a\}$
and
![]() $(g^{\bar ba})$
is the inverse matrix of
$(g^{\bar ba})$
is the inverse matrix of
![]() $(g_{i\bar j})$
(see, e.g., [Reference Vezzoni31]). We apply (23) to a left-invariant Hermitian metric on an Oeljeklaus–Toma manifold of the form (22).
$(g_{i\bar j})$
(see, e.g., [Reference Vezzoni31]). We apply (23) to a left-invariant Hermitian metric on an Oeljeklaus–Toma manifold of the form (22).
We have
 $$ \begin{align*} g^{\bar i s+i}=\begin{cases} 0, \quad & \mbox{if }i\not\in\{p_1,\ldots, p_k\}\, , \\ -\frac{C_i}{A_iB_i-\lvert C_i\rvert^2},\quad & \mbox{otherwise}\, , \end{cases}\quad g^{\bar i i}=\frac{B_i}{A_iB_i-\lvert C_i\rvert^2}, \quad g^{\overline{ s+i}s+i }=\frac{A_i}{A_iB_i-\lvert C_i\rvert^2}, \end{align*} $$
$$ \begin{align*} g^{\bar i s+i}=\begin{cases} 0, \quad & \mbox{if }i\not\in\{p_1,\ldots, p_k\}\, , \\ -\frac{C_i}{A_iB_i-\lvert C_i\rvert^2},\quad & \mbox{otherwise}\, , \end{cases}\quad g^{\bar i i}=\frac{B_i}{A_iB_i-\lvert C_i\rvert^2}, \quad g^{\overline{ s+i}s+i }=\frac{A_i}{A_iB_i-\lvert C_i\rvert^2}, \end{align*} $$
and taking into account that the ideal
![]() $\mathfrak {I}$
is abelian, we have
$\mathfrak {I}$
is abelian, we have
 $$ \begin{align*}\rho_B(X,Y)=-\sum_{i=1}^4\rho_i(X,Y), \end{align*} $$
$$ \begin{align*}\rho_B(X,Y)=-\sum_{i=1}^4\rho_i(X,Y), \end{align*} $$
where
 $$ \begin{align*} \rho_1(X,Y)&=\sum_{a=1}^sg^{a\bar a}(\omega([[X,Y]^{1,0}, Z_a], \bar Z_a)-\frac{ \sqrt{-1}}{2}\omega([X,Y],Z_a-\bar Z_a)\\&\quad+\omega([[X,Y]^{0,1},\bar Z_a],Z_a)),\\ \rho_2(X,Y)&=\sum_{a=1}^sg^{s+a\overline {s+a}}(\omega([[X,Y]^{1,0}, W_a], \bar W_a)+\omega([[X,Y]^{0,1},\bar W_a], W_a)),\\ \rho_3(X,Y)&=\sum_{r=1}^kg^{p_r\overline{s+p_r}}\left(\omega([[X,Y]^{1,0}, Z_{p_r}], \bar W_{p_r})-\omega([X,Y],[Z_{p_r},\bar W_{p_r}])\right)\\&\quad+g^{\overline {p_r} s+p_r }\omega([[X,Y]^{0,1},\bar Z_{p_r}], W_{p_r})\, ,\\ \rho_4(X,Y)&=\sum_{r=1}^kg^{s+p_r\bar p_r}\left(\omega([[X,Y]^{1,0}, W_{p_r}], \bar Z_{p_r})+\omega([X,Y],[W_{p_r},\bar Z_{p_r}]))\right)\\&\quad+ g^{\overline{s+p_r} p_r }\omega([[X,Y]^{0,1},\bar W_{p_r}], Z_{p_r}). \end{align*} $$
$$ \begin{align*} \rho_1(X,Y)&=\sum_{a=1}^sg^{a\bar a}(\omega([[X,Y]^{1,0}, Z_a], \bar Z_a)-\frac{ \sqrt{-1}}{2}\omega([X,Y],Z_a-\bar Z_a)\\&\quad+\omega([[X,Y]^{0,1},\bar Z_a],Z_a)),\\ \rho_2(X,Y)&=\sum_{a=1}^sg^{s+a\overline {s+a}}(\omega([[X,Y]^{1,0}, W_a], \bar W_a)+\omega([[X,Y]^{0,1},\bar W_a], W_a)),\\ \rho_3(X,Y)&=\sum_{r=1}^kg^{p_r\overline{s+p_r}}\left(\omega([[X,Y]^{1,0}, Z_{p_r}], \bar W_{p_r})-\omega([X,Y],[Z_{p_r},\bar W_{p_r}])\right)\\&\quad+g^{\overline {p_r} s+p_r }\omega([[X,Y]^{0,1},\bar Z_{p_r}], W_{p_r})\, ,\\ \rho_4(X,Y)&=\sum_{r=1}^kg^{s+p_r\bar p_r}\left(\omega([[X,Y]^{1,0}, W_{p_r}], \bar Z_{p_r})+\omega([X,Y],[W_{p_r},\bar Z_{p_r}]))\right)\\&\quad+ g^{\overline{s+p_r} p_r }\omega([[X,Y]^{0,1},\bar W_{p_r}], Z_{p_r}). \end{align*} $$
Next, we focus on the computation of
![]() $\rho _B(Z_i,\bar Z_j).$
Thanks to (1), we easily obtain that
$\rho _B(Z_i,\bar Z_j).$
Thanks to (1), we easily obtain that
On the other hand,
 $$ \begin{align*} \rho_1(Z_i,\bar Z_i)&= -\frac{\sqrt{-1}}{2}\sum_{a=1}^sg^{a\bar a}\left(-\frac{\sqrt{-1}}{2}\omega(Z_i+\bar Z_i, Z_a-\bar Z_a)\right) &\\&= \,\frac{\sqrt{-1}}{2}g^{i\bar i}A_i=\frac{\sqrt{-1}}{2}\left(\frac{A_iB_i}{A_iB_i-\lvert C_i\rvert^2}\right). \end{align*} $$
$$ \begin{align*} \rho_1(Z_i,\bar Z_i)&= -\frac{\sqrt{-1}}{2}\sum_{a=1}^sg^{a\bar a}\left(-\frac{\sqrt{-1}}{2}\omega(Z_i+\bar Z_i, Z_a-\bar Z_a)\right) &\\&= \,\frac{\sqrt{-1}}{2}g^{i\bar i}A_i=\frac{\sqrt{-1}}{2}\left(\frac{A_iB_i}{A_iB_i-\lvert C_i\rvert^2}\right). \end{align*} $$
Moreover, we have
 $$ \begin{align*}\begin{aligned} \rho_2(Z_i,\bar Z_i)=& -\frac{\sqrt{-1}}{2}\sum_{a=1}^sg^{s+a\overline {s+a}} (\omega([Z_i, W_a], \bar W_a)+\omega([\bar Z_i,\bar W_a],W_a)\\ =&-\sqrt{-1}\sum_{a=1}^sg^{s+a\overline {s+a}}\Re\mathfrak e\, \omega([Z_i,W_a], \bar W_a). \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \rho_2(Z_i,\bar Z_i)=& -\frac{\sqrt{-1}}{2}\sum_{a=1}^sg^{s+a\overline {s+a}} (\omega([Z_i, W_a], \bar W_a)+\omega([\bar Z_i,\bar W_a],W_a)\\ =&-\sqrt{-1}\sum_{a=1}^sg^{s+a\overline {s+a}}\Re\mathfrak e\, \omega([Z_i,W_a], \bar W_a). \end{aligned} \end{align*} $$
Using (1), we have
Then
 $$ \begin{align*}\rho_2(Z_i,\bar Z_i)=\sqrt{-1}\frac{g^{s+i\overline{s+i}}B_i}{4}=\frac{\sqrt{-1}}{4}\frac{A_iB_i}{A_i B_i-\lvert C_i\rvert^2}. \end{align*} $$
$$ \begin{align*}\rho_2(Z_i,\bar Z_i)=\sqrt{-1}\frac{g^{s+i\overline{s+i}}B_i}{4}=\frac{\sqrt{-1}}{4}\frac{A_iB_i}{A_i B_i-\lvert C_i\rvert^2}. \end{align*} $$
Next, we observe that
which implies that
 $$ \begin{align} \rho_B(Z_i,\bar Z_i)=\!\begin{cases}-\sqrt{-1}\frac{3}{4}\left(1+\frac{\lvert C_{r}\rvert^2}{A_{p_r}B_{p_r}-\lvert C_{r}\rvert^2}\right),\quad & \!\!\!\!\!\mbox{if there exists } r=1,\ldots, k \,\, \mbox{such that } i=p_r, \\ -\sqrt{-1}\frac34, \quad & \!\!\!\!\!\mbox{if } i\not\in \{p_1,\ldots, p_k\}. \end{cases} \end{align} $$
$$ \begin{align} \rho_B(Z_i,\bar Z_i)=\!\begin{cases}-\sqrt{-1}\frac{3}{4}\left(1+\frac{\lvert C_{r}\rvert^2}{A_{p_r}B_{p_r}-\lvert C_{r}\rvert^2}\right),\quad & \!\!\!\!\!\mbox{if there exists } r=1,\ldots, k \,\, \mbox{such that } i=p_r, \\ -\sqrt{-1}\frac34, \quad & \!\!\!\!\!\mbox{if } i\not\in \{p_1,\ldots, p_k\}. \end{cases} \end{align} $$
We have
 $$ \begin{align*}\begin{aligned} \rho_3(Z_i,\bar Z_i)=&\sum_{j=1}^kg^{p_j\overline{s+p_j}}\omega([Z_i,\bar Z_i],[Z_{p_j},\bar W_{p_j}]) =-\frac{\sqrt{-1}}{2}\sum_{j=1}^kg^{p_j\overline{s+p_j}}\bar \lambda_{p_jp_j}\omega(Z_i+\bar Z_i, \bar W_{p_j}) \\ =& \begin{cases} 0,\quad & \mbox{if } i\not\in\{p_1,\ldots, p_k \}, \\ \frac{1}{2} g^{i\overline{s+i}}\bar \lambda_{ii}C_{i}, \quad &\mbox{otherwise}. \end{cases} \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \rho_3(Z_i,\bar Z_i)=&\sum_{j=1}^kg^{p_j\overline{s+p_j}}\omega([Z_i,\bar Z_i],[Z_{p_j},\bar W_{p_j}]) =-\frac{\sqrt{-1}}{2}\sum_{j=1}^kg^{p_j\overline{s+p_j}}\bar \lambda_{p_jp_j}\omega(Z_i+\bar Z_i, \bar W_{p_j}) \\ =& \begin{cases} 0,\quad & \mbox{if } i\not\in\{p_1,\ldots, p_k \}, \\ \frac{1}{2} g^{i\overline{s+i}}\bar \lambda_{ii}C_{i}, \quad &\mbox{otherwise}. \end{cases} \end{aligned} \end{align*} $$
We compute the three addends in the expression of
![]() $\rho _4$
separately:
$\rho _4$
separately:
 $$ \begin{align*} &\begin{aligned} \omega([[Z_i,\bar Z_i]^{1,0}, W_{p_j}], \bar Z_{p_j})=& -\frac{1}{2}\lambda_{ip_j}\bar C_{p_j} =&\!\!\!\!\begin{cases} 0, \quad & \mbox{if } i\not\in\{p_1,\ldots, p_k\}\quad\!\!\! \mbox{or } i\ne p_j, \\ -\frac{1}{2}\lambda_{ii} \bar C_i,\quad & \mbox{otherwise}, \end{cases} \end{aligned}\\ &\begin{aligned} \omega([Z_i,\bar Z_i],[W_{p_j},\bar Z_{p_j}])=& \frac{1}{2}\lambda_{p_jp_j}g_{\overline{i}s+p_j} =&\!\!\!\!\begin{cases}0, \quad& \mbox{if } i\not\in\{p_1,\ldots, p_k\}\quad\!\!\! \mbox{or } \,\, i\ne p_j, \\ \frac{1}{2}\lambda_{ii}\bar C_i,\quad & \mbox{otherwise}, \end{cases} \end{aligned}\\ &\begin{aligned} \omega([[Z_i,\bar Z_i]^{0,1},\bar W_{p_j}], Z_{p_j})=& \frac{1}{2}\bar \lambda_{ip_j}g_{\overline{s+p_j}p_j} =&\!\!\!\!\begin{cases}0, \quad & \mbox{if } i\ne p_j, \\ \frac{1}{2}\bar \lambda_{ii}C_{i}, \quad & \mbox{otherwise}. \end{cases} \end{aligned} \end{align*} $$
$$ \begin{align*} &\begin{aligned} \omega([[Z_i,\bar Z_i]^{1,0}, W_{p_j}], \bar Z_{p_j})=& -\frac{1}{2}\lambda_{ip_j}\bar C_{p_j} =&\!\!\!\!\begin{cases} 0, \quad & \mbox{if } i\not\in\{p_1,\ldots, p_k\}\quad\!\!\! \mbox{or } i\ne p_j, \\ -\frac{1}{2}\lambda_{ii} \bar C_i,\quad & \mbox{otherwise}, \end{cases} \end{aligned}\\ &\begin{aligned} \omega([Z_i,\bar Z_i],[W_{p_j},\bar Z_{p_j}])=& \frac{1}{2}\lambda_{p_jp_j}g_{\overline{i}s+p_j} =&\!\!\!\!\begin{cases}0, \quad& \mbox{if } i\not\in\{p_1,\ldots, p_k\}\quad\!\!\! \mbox{or } \,\, i\ne p_j, \\ \frac{1}{2}\lambda_{ii}\bar C_i,\quad & \mbox{otherwise}, \end{cases} \end{aligned}\\ &\begin{aligned} \omega([[Z_i,\bar Z_i]^{0,1},\bar W_{p_j}], Z_{p_j})=& \frac{1}{2}\bar \lambda_{ip_j}g_{\overline{s+p_j}p_j} =&\!\!\!\!\begin{cases}0, \quad & \mbox{if } i\ne p_j, \\ \frac{1}{2}\bar \lambda_{ii}C_{i}, \quad & \mbox{otherwise}. \end{cases} \end{aligned} \end{align*} $$
It follows
and, for
![]() $i\in \{p_1,\ldots , p_k\}$
,
$i\in \{p_1,\ldots , p_k\}$
,
 $$ \begin{align*}&\rho_3(Z_{i},\bar Z_{i})+\rho_4(Z_{i},\bar Z_{i})\\&\quad=-\frac{1}{2} g^{i\overline{s+i}}\bar \lambda_{ii} C_i -g^{s+i\overline{i}}\frac{1}{2}\lambda_{ii}\bar C_i +g^{s+i\overline{i}}\frac{1}{2}\lambda_{ii}\bar C_i+g^{\overline{s+i}i}\frac{1}{2}\bar \lambda_{ii}C_i=0. \end{align*} $$
$$ \begin{align*}&\rho_3(Z_{i},\bar Z_{i})+\rho_4(Z_{i},\bar Z_{i})\\&\quad=-\frac{1}{2} g^{i\overline{s+i}}\bar \lambda_{ii} C_i -g^{s+i\overline{i}}\frac{1}{2}\lambda_{ii}\bar C_i +g^{s+i\overline{i}}\frac{1}{2}\lambda_{ii}\bar C_i+g^{\overline{s+i}i}\frac{1}{2}\bar \lambda_{ii}C_i=0. \end{align*} $$
Now, we focus on the calculation of
![]() $\rho _B(Z_i,\bar W_j)$
. We have
$\rho _B(Z_i,\bar W_j)$
. We have
 $$ \begin{align*}\begin{aligned} \rho_1(Z_i,\bar W_j)=&\, \sum_{a=1}^sg^{a\bar a}\bar \lambda_{ij}\left(-\frac{\sqrt{-1}}{2}\omega(\bar W_j, Z_a-\bar Z_a)+\omega([\bar W_j, \bar Z_a], Z_a)\right)\\ =&\, \begin{cases}0, \quad &\mbox{if } i=j\in\{p_1,\ldots, p_k\}\,, \\ \sqrt{-1}g^{i\bar i}C_i\bar \lambda_{ii}\left(\frac{\sqrt{-1}}{2}-\bar \lambda_{ii}\right), \quad & \mbox{otherwise} , \end{cases} \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \rho_1(Z_i,\bar W_j)=&\, \sum_{a=1}^sg^{a\bar a}\bar \lambda_{ij}\left(-\frac{\sqrt{-1}}{2}\omega(\bar W_j, Z_a-\bar Z_a)+\omega([\bar W_j, \bar Z_a], Z_a)\right)\\ =&\, \begin{cases}0, \quad &\mbox{if } i=j\in\{p_1,\ldots, p_k\}\,, \\ \sqrt{-1}g^{i\bar i}C_i\bar \lambda_{ii}\left(\frac{\sqrt{-1}}{2}-\bar \lambda_{ii}\right), \quad & \mbox{otherwise} , \end{cases} \end{aligned} \end{align*} $$
and since
![]() $\mathfrak {I}$
is abelian
$\mathfrak {I}$
is abelian
Furthermore,
 $$ \begin{align*}\begin{aligned} \rho_3(Z_i,\bar W_j)=&\, \sum_{j=1}^kg^{\overline {p_j} s+p_j }\omega([[Z_i,\bar W_j]^{0,1},\bar Z_{p_j}], W_{p_j})=-\sqrt{-1}\sum_{j=1}^kg^{\overline {p_j} s+p_j }\bar \lambda_{ij}\bar \lambda_{p_j p_j}g_{\overline{s+j}s+p_j}\\ =&\, \begin{cases}0, \quad & \mbox{if } i=j\in \{p_1,\ldots, p_k\}, \\ -\sqrt{-1}\bar \lambda_{jj}^2g^{\overline{j}s+j}B_j,\quad & \mbox{otherwise},\end{cases} \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \rho_3(Z_i,\bar W_j)=&\, \sum_{j=1}^kg^{\overline {p_j} s+p_j }\omega([[Z_i,\bar W_j]^{0,1},\bar Z_{p_j}], W_{p_j})=-\sqrt{-1}\sum_{j=1}^kg^{\overline {p_j} s+p_j }\bar \lambda_{ij}\bar \lambda_{p_j p_j}g_{\overline{s+j}s+p_j}\\ =&\, \begin{cases}0, \quad & \mbox{if } i=j\in \{p_1,\ldots, p_k\}, \\ -\sqrt{-1}\bar \lambda_{jj}^2g^{\overline{j}s+j}B_j,\quad & \mbox{otherwise},\end{cases} \end{aligned} \end{align*} $$
and
 $$ \begin{align*}\begin{aligned} \rho_4(Z_i,\bar W_j)=&\sum_{j=1}^kg^{s+p_j\bar p_j}\omega([Z_i,\bar W_j],[W_{p_j},\bar Z_{p_j}])=\sqrt{-1}\sum_{j=1}^kg^{s+p_j\bar p_j}\bar \lambda_{ij}\lambda_{p_jp_j}g_{\overline{s+j}s+p_j} \\ =&\, \begin{cases}0, \quad &\mbox{if } i=j\in \{p_1,\ldots, p_k\},\\ \sqrt{-1}g^{s+j\bar j}\bar \lambda_{jj}\lambda_{jj}B_j,\quad & \mbox{otherwise}. \end{cases} \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \rho_4(Z_i,\bar W_j)=&\sum_{j=1}^kg^{s+p_j\bar p_j}\omega([Z_i,\bar W_j],[W_{p_j},\bar Z_{p_j}])=\sqrt{-1}\sum_{j=1}^kg^{s+p_j\bar p_j}\bar \lambda_{ij}\lambda_{p_jp_j}g_{\overline{s+j}s+p_j} \\ =&\, \begin{cases}0, \quad &\mbox{if } i=j\in \{p_1,\ldots, p_k\},\\ \sqrt{-1}g^{s+j\bar j}\bar \lambda_{jj}\lambda_{jj}B_j,\quad & \mbox{otherwise}. \end{cases} \end{aligned} \end{align*} $$
It follows that
![]() $\rho _B(Z_i,\bar W_j)\ne 0 $
if and only if
$\rho _B(Z_i,\bar W_j)\ne 0 $
if and only if
![]() $i=j\in \{p_1,\ldots , p_k\}.$
In such a case, we have
$i=j\in \{p_1,\ldots , p_k\}.$
In such a case, we have
 $$ \begin{align*}\begin{aligned} \rho_B(Z_j,\bar W_j)=& -\sqrt{-1}\left(g^{s+j\overline{j}}B_j\left(\lvert\lambda_{jj}\rvert^2-\bar \lambda_{jj}^2\right)+g^{j\bar j}C_j\bar \lambda_{jj}\left(\frac{\sqrt{-1}}{2}-\bar \lambda_{jj}\right)\right). \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \rho_B(Z_j,\bar W_j)=& -\sqrt{-1}\left(g^{s+j\overline{j}}B_j\left(\lvert\lambda_{jj}\rvert^2-\bar \lambda_{jj}^2\right)+g^{j\bar j}C_j\bar \lambda_{jj}\left(\frac{\sqrt{-1}}{2}-\bar \lambda_{jj}\right)\right). \end{aligned} \end{align*} $$
Since
 $$ \begin{align*}g^{s+j\bar j }B_j=-\frac{B_jC_j}{A_jB_j-\lvert C_j\rvert^2}\quad \mbox{and }\quad g^{j\bar j}C_j=\frac{B_jC_j}{A_jB_j-\lvert C_j\rvert^2}, \end{align*} $$
$$ \begin{align*}g^{s+j\bar j }B_j=-\frac{B_jC_j}{A_jB_j-\lvert C_j\rvert^2}\quad \mbox{and }\quad g^{j\bar j}C_j=\frac{B_jC_j}{A_jB_j-\lvert C_j\rvert^2}, \end{align*} $$
we infer
 $$ \begin{align*}\rho_B(Z_j,\bar W_j)=-\sqrt{-1}\left(\bar\lambda_{jj}\left(\frac{\sqrt{-1}}{2}-\bar\lambda_{jj}\right)-\left(\lvert\lambda_{jj}\rvert^2-\bar\lambda_{jj}^2\right)\right)\frac{B_jC_j}{A_jB_j-\lvert C_j\rvert^2}. \end{align*} $$
$$ \begin{align*}\rho_B(Z_j,\bar W_j)=-\sqrt{-1}\left(\bar\lambda_{jj}\left(\frac{\sqrt{-1}}{2}-\bar\lambda_{jj}\right)-\left(\lvert\lambda_{jj}\rvert^2-\bar\lambda_{jj}^2\right)\right)\frac{B_jC_j}{A_jB_j-\lvert C_j\rvert^2}. \end{align*} $$
Taking into account that
![]() $\lambda _{jj}=-\frac {\sqrt {-1}}{4}-\frac {c_{jj}}{2}$
, we obtain
$\lambda _{jj}=-\frac {\sqrt {-1}}{4}-\frac {c_{jj}}{2}$
, we obtain
 $$ \begin{align*}\rho_B(Z_j,\bar W_j)=-\sqrt{-1}\left(-\frac{3}{16}-\frac{c_{jj}^2}{4}-\frac{\sqrt{-1}c_{jj}}{4}\right)\frac{B_jC_j}{A_jB_j-\lvert C_j\rvert^2}, \end{align*} $$
$$ \begin{align*}\rho_B(Z_j,\bar W_j)=-\sqrt{-1}\left(-\frac{3}{16}-\frac{c_{jj}^2}{4}-\frac{\sqrt{-1}c_{jj}}{4}\right)\frac{B_jC_j}{A_jB_j-\lvert C_j\rvert^2}, \end{align*} $$
and the claim follows.
Corollary 5.4 Let
![]() $\omega $
be a left-invariant pluriclosed Hermitian metric on an Oeljeklaus–Toma manifold M. Then
$\omega $
be a left-invariant pluriclosed Hermitian metric on an Oeljeklaus–Toma manifold M. Then
![]() $\omega $
lifts to an algebraic expanding soliton of the pluriclosed flow on the universal covering of M if and only if it takes the following diagonal expression with respect to a coframe
$\omega $
lifts to an algebraic expanding soliton of the pluriclosed flow on the universal covering of M if and only if it takes the following diagonal expression with respect to a coframe
![]() $\{\omega ^1,\dots ,\omega ^s,\gamma ^1,\dots ,\gamma ^s\}$
satisfying (
1
) and (
15
):
$\{\omega ^1,\dots ,\omega ^s,\gamma ^1,\dots ,\gamma ^s\}$
satisfying (
1
) and (
15
):
 $$ \begin{align} \omega=\sqrt{-1}\sum_{i=1}^sA\omega^i\wedge \bar \omega^i+ B_i\gamma^i\wedge \bar \gamma^i. \end{align} $$
$$ \begin{align} \omega=\sqrt{-1}\sum_{i=1}^sA\omega^i\wedge \bar \omega^i+ B_i\gamma^i\wedge \bar \gamma^i. \end{align} $$
Proof Let
![]() $\omega $
be a pluriclosed left-invariant metric on an Oeljeklaus–Toma manifold M. In view of [Reference Lauret15, Section 7],
$\omega $
be a pluriclosed left-invariant metric on an Oeljeklaus–Toma manifold M. In view of [Reference Lauret15, Section 7],
![]() $\omega $
lifts to an algebraic expanding soliton of the pluriclosed flow on the universal covering of M if and only if
$\omega $
lifts to an algebraic expanding soliton of the pluriclosed flow on the universal covering of M if and only if
for some
![]() $c\in {\mathbb R}_{-}$
and some derivation D of
$c\in {\mathbb R}_{-}$
and some derivation D of
![]() $\mathfrak {g}$
such that
$\mathfrak {g}$
such that
![]() $DJ=JD$
.
$DJ=JD$
.
Assume that
![]() $\omega $
takes the expression in formula (25). Proposition 5.3 implies that
$\omega $
takes the expression in formula (25). Proposition 5.3 implies that
![]() $\rho _B$
is represented with respect to the basis
$\rho _B$
is represented with respect to the basis
![]() $\{Z_1,\ldots , Z_s,W_1,\ldots , W_s\}$
by the matrix
$\{Z_1,\ldots , Z_s,W_1,\ldots , W_s\}$
by the matrix
 $$ \begin{align*} P=-\frac{3}{4A} \begin{pmatrix} \mathrm{I}_{\mathfrak{h}} & 0\\ 0 & 0 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} P=-\frac{3}{4A} \begin{pmatrix} \mathrm{I}_{\mathfrak{h}} & 0\\ 0 & 0 \end{pmatrix}. \end{align*} $$
Since
 $$ \begin{align*} \frac{3}{4A} \begin{pmatrix} 0 & 0\\ 0 & \mathrm{I}_{\mathfrak{I}} \end{pmatrix} \end{align*} $$
$$ \begin{align*} \frac{3}{4A} \begin{pmatrix} 0 & 0\\ 0 & \mathrm{I}_{\mathfrak{I}} \end{pmatrix} \end{align*} $$
induces a symmetric derivation on
![]() $\mathfrak {g}$
,
$\mathfrak {g}$
,
![]() $\omega $
lifts to an algebraic expanding soliton of the pluriclosed flow on the universal covering of M and the first part of the claim follows.
$\omega $
lifts to an algebraic expanding soliton of the pluriclosed flow on the universal covering of M and the first part of the claim follows.
In order to prove the second part of the statement, we need some preliminary observations on derivations D of
![]() $\mathfrak {g}$
that commute with J, i.e., such that
$\mathfrak {g}$
that commute with J, i.e., such that
We can write
 $$ \begin{align*}DZ_i= \sum_{j=1}^s k^i_jZ_j+m^i_jW_j\quad \mbox{ and }\quad D\bar Z_i= \sum_{j=1}^sl^i_j\bar Z_j+ r^i_j\bar W_j. \end{align*} $$
$$ \begin{align*}DZ_i= \sum_{j=1}^s k^i_jZ_j+m^i_jW_j\quad \mbox{ and }\quad D\bar Z_i= \sum_{j=1}^sl^i_j\bar Z_j+ r^i_j\bar W_j. \end{align*} $$
Since D is a derivation, we have, for all
![]() $i=1,\ldots , s$
,
$i=1,\ldots , s$
,
On the other hand,
 $$ \begin{align*}\begin{aligned} D[Z_i,\bar Z_i]=&\, -\frac{\sqrt{-1}}{2}\left(\sum_{j=1}^sk^i_jZ_j+l^i_j\bar Z_j+m^i_jW_j+r^i_j\bar W_j \right)\, ,\\ [DZ_i,\bar Z_i]=&\, -\frac{\sqrt{-1}}{2}k^i_i(Z_i+\bar Z_i)-\sum_{j=1}^sm^i_j\lambda_{ij}W_j,\\ [Z_i,D\bar Z_i]=&\, -\frac{\sqrt{-1}}{2}l^i_j(Z_i+\bar Z_i)+\sum_{j=1}^sr^i_j\bar \lambda_{ij}\bar W_j \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} D[Z_i,\bar Z_i]=&\, -\frac{\sqrt{-1}}{2}\left(\sum_{j=1}^sk^i_jZ_j+l^i_j\bar Z_j+m^i_jW_j+r^i_j\bar W_j \right)\, ,\\ [DZ_i,\bar Z_i]=&\, -\frac{\sqrt{-1}}{2}k^i_i(Z_i+\bar Z_i)-\sum_{j=1}^sm^i_j\lambda_{ij}W_j,\\ [Z_i,D\bar Z_i]=&\, -\frac{\sqrt{-1}}{2}l^i_j(Z_i+\bar Z_i)+\sum_{j=1}^sr^i_j\bar \lambda_{ij}\bar W_j \end{aligned} \end{align*} $$
and
 $$ \begin{align*}\begin{aligned} 0=&\, D[Z_i,\bar Z_i]-[DZ_i,\bar Z_i]-[Z_i,D\bar Z_i]\\ =&\, -\frac{\sqrt{-1}}{2}\sum_{j\ne i}k^i_jZ_j+l^i_j\bar Z_j+\frac{\sqrt{-1}}{2}l^i_iZ_i+\frac{\sqrt{-1}}{2}k^i_i\bar Z_i\\&\,+\sum_{j=1}^sm^i_j\left(\lambda_{ij}-\frac{\sqrt{-1}}{2}\right)W_j-r^i_j\left(\frac{\sqrt{-1}}{2}+\bar \lambda_{ij}\right)\bar W_j, \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} 0=&\, D[Z_i,\bar Z_i]-[DZ_i,\bar Z_i]-[Z_i,D\bar Z_i]\\ =&\, -\frac{\sqrt{-1}}{2}\sum_{j\ne i}k^i_jZ_j+l^i_j\bar Z_j+\frac{\sqrt{-1}}{2}l^i_iZ_i+\frac{\sqrt{-1}}{2}k^i_i\bar Z_i\\&\,+\sum_{j=1}^sm^i_j\left(\lambda_{ij}-\frac{\sqrt{-1}}{2}\right)W_j-r^i_j\left(\frac{\sqrt{-1}}{2}+\bar \lambda_{ij}\right)\bar W_j, \end{aligned} \end{align*} $$
which forces
![]() $DZ_i, D\bar Z_i=0$
, for all
$DZ_i, D\bar Z_i=0$
, for all
![]() $i=1,\ldots , s$
. It follows that
$i=1,\ldots , s$
. It follows that
![]() $D_{|\mathfrak {h}}=0$
.
$D_{|\mathfrak {h}}=0$
.
Moreover, for all
![]() $I,I'\in \mathfrak {J}$
, we have
$I,I'\in \mathfrak {J}$
, we have
which implies that
Assume that
 $$ \begin{align*}DW_i= \sum_{j=1}^s k^{s+i}_jZ_j+m^{s+i}_jW_j \quad \mbox{ and }\quad D\bar W_i= \sum_{j=1}^sl^{s+i}_j\bar Z_j+ r^{s+i}_j\bar W_j, \end{align*} $$
$$ \begin{align*}DW_i= \sum_{j=1}^s k^{s+i}_jZ_j+m^{s+i}_jW_j \quad \mbox{ and }\quad D\bar W_i= \sum_{j=1}^sl^{s+i}_j\bar Z_j+ r^{s+i}_j\bar W_j, \end{align*} $$
then
 $$ \begin{align*}[DW_i,\bar W_i]=\sum_{j=1}^sk^{s+i}_j[Z_j,\bar W_i]\in\mathfrak{J}^{0,1} \quad \mbox{ and }\quad [W_i,D\bar W_i]=\sum_{j=1}^sl^{s+i}_j[W_i,\bar Z_j]\in \mathfrak{J}^{1,0}. \end{align*} $$
$$ \begin{align*}[DW_i,\bar W_i]=\sum_{j=1}^sk^{s+i}_j[Z_j,\bar W_i]\in\mathfrak{J}^{0,1} \quad \mbox{ and }\quad [W_i,D\bar W_i]=\sum_{j=1}^sl^{s+i}_j[W_i,\bar Z_j]\in \mathfrak{J}^{1,0}. \end{align*} $$
This implies that
 $$ \begin{align*}DW_i= \sum_{j=1}^sm^{s+i}_jW_j\, ,\quad D\bar W_i= \sum_{j=1}^s r^{s+i}_j\bar W_j, \end{align*} $$
$$ \begin{align*}DW_i= \sum_{j=1}^sm^{s+i}_jW_j\, ,\quad D\bar W_i= \sum_{j=1}^s r^{s+i}_j\bar W_j, \end{align*} $$
i.e.,
![]() $D(\mathfrak {J})\subseteq \mathfrak {J}$
. Moreover, for all
$D(\mathfrak {J})\subseteq \mathfrak {J}$
. Moreover, for all
![]() $i=1,\ldots , s$
, we have that
$i=1,\ldots , s$
, we have that
 $$ \begin{align*}D[Z_i, W_i]=-\lambda_{ii}DW_i=-\sum_{j=1}^s\lambda_{ii}m^{s+i}_jW_j, \end{align*} $$
$$ \begin{align*}D[Z_i, W_i]=-\lambda_{ii}DW_i=-\sum_{j=1}^s\lambda_{ii}m^{s+i}_jW_j, \end{align*} $$
whereas
![]() $[DZ_i,W_i]=0$
and
$[DZ_i,W_i]=0$
and
 $$ \begin{align*}[Z_i, DW_i]=-\sum_{j=1}^sm^{s+i}_j\lambda_{ij}W_j. \end{align*} $$
$$ \begin{align*}[Z_i, DW_i]=-\sum_{j=1}^sm^{s+i}_j\lambda_{ij}W_j. \end{align*} $$
Using again the fact that D is a derivation, we have
where
With analogous computations, we infer
Clearly,
![]() $i\in J_i$
. On the other hand, for all
$i\in J_i$
. On the other hand, for all
![]() $i=1,\ldots , s$
, we know that
$i=1,\ldots , s$
, we know that
![]() $\Im \mathfrak {m}(\lambda _{ii})\ne 0 $
, whereas, for all
$\Im \mathfrak {m}(\lambda _{ii})\ne 0 $
, whereas, for all
![]() $i\ne j$
,
$i\ne j$
,
![]() $\lambda _{ij}\in {\mathbb R}.$
This guarantees that, for all
$\lambda _{ij}\in {\mathbb R}.$
This guarantees that, for all
![]() $i=1,\ldots , s$
,
$i=1,\ldots , s$
,
This allows us to write
From the relations above, we obtain that
First of all, we suppose that
![]() $\omega $
is a pluriclosed Hermitian metric which takes the following diagonal expression with respect to a coframe
$\omega $
is a pluriclosed Hermitian metric which takes the following diagonal expression with respect to a coframe
![]() $\{\omega ^1,\dots ,\omega ^s,\gamma ^1,\dots ,\gamma ^s\}$
satisfying (1) and (15):
$\{\omega ^1,\dots ,\omega ^s,\gamma ^1,\dots ,\gamma ^s\}$
satisfying (1) and (15):
 $$ \begin{align*}\omega=\sqrt{-1}\sum_{i=1}^sA_i\omega^i\wedge \bar \omega^i+ B_i\gamma^i\wedge \bar \gamma^i, \end{align*} $$
$$ \begin{align*}\omega=\sqrt{-1}\sum_{i=1}^sA_i\omega^i\wedge \bar \omega^i+ B_i\gamma^i\wedge \bar \gamma^i, \end{align*} $$
such that there exist
![]() $i, j\in \{1,\ldots , s\}$
such that
$i, j\in \{1,\ldots , s\}$
such that
![]() $A_i\ne A_j$
and we suppose that
$A_i\ne A_j$
and we suppose that
![]() $\omega $
is an algebraic soliton. Thanks to the facts regarding derivations proved before, we have that
$\omega $
is an algebraic soliton. Thanks to the facts regarding derivations proved before, we have that
 $$ \begin{align*}\begin{aligned} -\sqrt{-1}\frac34=\rho_B(Z_i,\bar Z_i)=&\, c\omega(Z_i,\bar Z_i)+ \frac12\left(\omega(DZ_i,\bar Z_i)+\omega(Z_i, D\bar Z_i)\right)=\sqrt{-1}cA_i,\\ -\sqrt{-1}\frac34=\rho_B(Z_j,\bar Z_j)=&\, c\omega(Z_j,\bar Z_j)+ \frac12\left(\omega(DZ_j,\bar Z_j)+\omega(Z_j, D\bar Z_j)\right)=\sqrt{-1}cA_j, \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} -\sqrt{-1}\frac34=\rho_B(Z_i,\bar Z_i)=&\, c\omega(Z_i,\bar Z_i)+ \frac12\left(\omega(DZ_i,\bar Z_i)+\omega(Z_i, D\bar Z_i)\right)=\sqrt{-1}cA_i,\\ -\sqrt{-1}\frac34=\rho_B(Z_j,\bar Z_j)=&\, c\omega(Z_j,\bar Z_j)+ \frac12\left(\omega(DZ_j,\bar Z_j)+\omega(Z_j, D\bar Z_j)\right)=\sqrt{-1}cA_j, \end{aligned} \end{align*} $$
which is impossible, since
![]() $A_i\ne A_j$
.
$A_i\ne A_j$
.
Now, suppose that
![]() $\omega $
is a pluriclosed metric on M which is not diagonal. So, we suppose that there exists
$\omega $
is a pluriclosed metric on M which is not diagonal. So, we suppose that there exists
![]() $\tilde {j}=1,\ldots , s$
such that
$\tilde {j}=1,\ldots , s$
such that
![]() $C_{\tilde {j}}\ne 0.$
Then assume that there exist a constant
$C_{\tilde {j}}\ne 0.$
Then assume that there exist a constant
![]() $c\in \mathbb {R}$
and
$c\in \mathbb {R}$
and
![]() $D\in \mathrm {Der(}\mathfrak {g})$
such that
$D\in \mathrm {Der(}\mathfrak {g})$
such that
On the other hand,
 $$ \begin{align*}\begin{aligned} 0\kern1pt{=}\kern1pt\rho_B(W_{\tilde{j}},\bar W_{\tilde{j}})=&\, c\omega(W_{\tilde{j}},\bar W_{\tilde{j}})+ \frac12\left(\omega(DW_{\tilde{j}},\bar W_{\tilde{j}})+\omega(W_{\tilde{j}}, D\bar W_{\tilde{j}})\right)=\sqrt{-1}cB_{\tilde{j}}+\frac{\sqrt{-1}}{2}(r_{\tilde{j}}^{s+\tilde{j}}+m_{\tilde{j}}^{s+\tilde{j}})B_{\tilde{j}}, \\ \rho_B(Z_{\tilde{j}},\bar W_{\tilde{j}})= & c\omega(Z_{\tilde{j}},\bar W_{\tilde{j}})+ \frac{1}{2}\left(\omega(DZ_{\tilde{j}},\bar W_{\tilde{j}})+\omega(Z_{\tilde{j}}, D\bar W_{\tilde{j}})\right)=\sqrt{-1}cC_{\tilde{j}}+\frac{\sqrt{-1}}{2}r^{s+\tilde{j}}_{\tilde{j}}C_{\tilde{j}}\, ,\\ \rho_B(\bar Z_{\tilde{j}}, W_{\tilde{j}})=& c\omega(\bar Z_{\tilde{j}}, W_{\tilde{j}})+ \frac12\left(\omega(D\bar Z_{\tilde{j}}, W_{\tilde{j}})+\omega(\bar Z_{\tilde{j}}, D W_{\tilde{j}})\right)=-\sqrt{-1}c\bar C_{\tilde{j}}-\frac{\sqrt{-1}}{2}m^{s+\tilde{j}}_{\tilde{j}}\bar C_{\tilde{j}}, \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} 0\kern1pt{=}\kern1pt\rho_B(W_{\tilde{j}},\bar W_{\tilde{j}})=&\, c\omega(W_{\tilde{j}},\bar W_{\tilde{j}})+ \frac12\left(\omega(DW_{\tilde{j}},\bar W_{\tilde{j}})+\omega(W_{\tilde{j}}, D\bar W_{\tilde{j}})\right)=\sqrt{-1}cB_{\tilde{j}}+\frac{\sqrt{-1}}{2}(r_{\tilde{j}}^{s+\tilde{j}}+m_{\tilde{j}}^{s+\tilde{j}})B_{\tilde{j}}, \\ \rho_B(Z_{\tilde{j}},\bar W_{\tilde{j}})= & c\omega(Z_{\tilde{j}},\bar W_{\tilde{j}})+ \frac{1}{2}\left(\omega(DZ_{\tilde{j}},\bar W_{\tilde{j}})+\omega(Z_{\tilde{j}}, D\bar W_{\tilde{j}})\right)=\sqrt{-1}cC_{\tilde{j}}+\frac{\sqrt{-1}}{2}r^{s+\tilde{j}}_{\tilde{j}}C_{\tilde{j}}\, ,\\ \rho_B(\bar Z_{\tilde{j}}, W_{\tilde{j}})=& c\omega(\bar Z_{\tilde{j}}, W_{\tilde{j}})+ \frac12\left(\omega(D\bar Z_{\tilde{j}}, W_{\tilde{j}})+\omega(\bar Z_{\tilde{j}}, D W_{\tilde{j}})\right)=-\sqrt{-1}c\bar C_{\tilde{j}}-\frac{\sqrt{-1}}{2}m^{s+\tilde{j}}_{\tilde{j}}\bar C_{\tilde{j}}, \end{aligned} \end{align*} $$
which implies that
On the other hand,
where
 $$ \begin{align*}K=\left(\frac{3}{16}+\frac{c_{\tilde{j}\tilde{j}}^2}{4}+\frac{\sqrt{-1}c_{\tilde{j}\tilde{j}}}{4}\right)\frac{B_{\tilde{j}}}{A_{\tilde{j}}B_{\tilde{j}}-\lvert C_{\tilde{j}}\rvert^2}. \end{align*} $$
$$ \begin{align*}K=\left(\frac{3}{16}+\frac{c_{\tilde{j}\tilde{j}}^2}{4}+\frac{\sqrt{-1}c_{\tilde{j}\tilde{j}}}{4}\right)\frac{B_{\tilde{j}}}{A_{\tilde{j}}B_{\tilde{j}}-\lvert C_{\tilde{j}}\rvert^2}. \end{align*} $$
Then
and
From this, we obtain that
On the other hand, we have
 $$ \begin{align*}&-\sqrt{-1}\frac34\left(1+\frac{\lvert C_{\tilde{j}}\rvert^2}{A_{\tilde{j}}B_{\tilde{j}}-\lvert C_{\tilde{j}}\rvert^2}\right)= \rho_B(Z_{\tilde{j}},\bar Z_{\tilde{j}})\\&\quad= c\omega(Z_{\tilde{j}},\bar Z_{\tilde{j}})+ \frac12\left(\omega(DZ_{\tilde{j}},\bar Z_{\tilde{j}})+\omega(Z_{\tilde{j}},D\bar Z_{\tilde{j}})\right)=\sqrt{-1}cA_{\tilde{j}}, \end{align*} $$
$$ \begin{align*}&-\sqrt{-1}\frac34\left(1+\frac{\lvert C_{\tilde{j}}\rvert^2}{A_{\tilde{j}}B_{\tilde{j}}-\lvert C_{\tilde{j}}\rvert^2}\right)= \rho_B(Z_{\tilde{j}},\bar Z_{\tilde{j}})\\&\quad= c\omega(Z_{\tilde{j}},\bar Z_{\tilde{j}})+ \frac12\left(\omega(DZ_{\tilde{j}},\bar Z_{\tilde{j}})+\omega(Z_{\tilde{j}},D\bar Z_{\tilde{j}})\right)=\sqrt{-1}cA_{\tilde{j}}, \end{align*} $$
which implies that c must be negative. From this, the claim follows.
Corollary 5.5 Let
![]() $\omega $
be a pluriclosed Hermitian metric on an Oeljeklaus–Toma manifold which takes the form (16). Then the pluriclosed flow starting from
$\omega $
be a pluriclosed Hermitian metric on an Oeljeklaus–Toma manifold which takes the form (16). Then the pluriclosed flow starting from
![]() $\omega $
is equivalent to the following system of ODEs:
$\omega $
is equivalent to the following system of ODEs:
 $$ \begin{align} \begin{cases} A_i'=\frac{3}{4},\quad &\mbox{if } i\not\in\{p_1,\ldots, p_k\}, \\ A_{p_r}'=\frac{3}{4}\left(1+\frac{\lvert C_{r}\rvert^2}{A_{p_r}B_{p_r}-\lvert C_r\rvert^2}\right),\quad& \mbox{for all } r=1,\ldots, k\, , \\ B_j'=0,\quad &\mbox{for all }j=1,\ldots, s\, , \\ C_r'= -\left(\frac{3}{16}+\frac{c_{p_rp_r}^2}{4}+\frac{\sqrt{-1}c_{p_rp_r}}{4}\right)\frac{B_{p_r}C_r}{A_{p_r}B_{p_r}-|C_r|^2},\quad &\mbox{for all } r=1,\ldots, k\, .\end{cases} \end{align} $$
$$ \begin{align} \begin{cases} A_i'=\frac{3}{4},\quad &\mbox{if } i\not\in\{p_1,\ldots, p_k\}, \\ A_{p_r}'=\frac{3}{4}\left(1+\frac{\lvert C_{r}\rvert^2}{A_{p_r}B_{p_r}-\lvert C_r\rvert^2}\right),\quad& \mbox{for all } r=1,\ldots, k\, , \\ B_j'=0,\quad &\mbox{for all }j=1,\ldots, s\, , \\ C_r'= -\left(\frac{3}{16}+\frac{c_{p_rp_r}^2}{4}+\frac{\sqrt{-1}c_{p_rp_r}}{4}\right)\frac{B_{p_r}C_r}{A_{p_r}B_{p_r}-|C_r|^2},\quad &\mbox{for all } r=1,\ldots, k\, .\end{cases} \end{align} $$
Moreover,
![]() $\lvert C_r\rvert $
is bounded, for all
$\lvert C_r\rvert $
is bounded, for all
![]() $r =1,\ldots , k$
, and the solution exists for all
$r =1,\ldots , k$
, and the solution exists for all
![]() $ t\in [0,+\infty )$
and
$ t\in [0,+\infty )$
and
![]() $A_i\sim \frac {3}{4}t$
, as
$A_i\sim \frac {3}{4}t$
, as
![]() $t\to +\infty ,$
for all
$t\to +\infty ,$
for all
![]() $ i=1,\ldots , s.$
$ i=1,\ldots , s.$
In particular,
as
![]() $t\to \infty $
.
$t\to \infty $
.
Proof Observe that, for every
![]() $ r\in \{1,\ldots , k\}$
,
$ r\in \{1,\ldots , k\}$
,
 $$ \begin{align*}\begin{aligned} (\lvert C_r\rvert^2)'=&\, - \left(\frac{3}{8}+\frac{c_{p_rp_r}^2}{2}\right)\frac{B_{p_r}\lvert C_r\rvert^2}{A_{p_r}B_{p_r}-\lvert C_r\rvert^2}\le 0\, , \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} (\lvert C_r\rvert^2)'=&\, - \left(\frac{3}{8}+\frac{c_{p_rp_r}^2}{2}\right)\frac{B_{p_r}\lvert C_r\rvert^2}{A_{p_r}B_{p_r}-\lvert C_r\rvert^2}\le 0\, , \end{aligned} \end{align*} $$
which guarantees that
![]() $\lvert C_r\rvert ^2$
is bounded. On the other hand, denote, for all
$\lvert C_r\rvert ^2$
is bounded. On the other hand, denote, for all
![]() $ r=1,\ldots , k$
,
$ r=1,\ldots , k$
,
We have that
 $$ \begin{align*}u_r'=A^{\prime}_{p_r}B_{p_r}-(\lvert C_r\rvert^2)'=\frac{3}{4}B_{p_r}+\left(\frac{9}{8}+\frac{c^2_{p_rp_r}}{2}\right)\frac{B_{p_r}\lvert C_r\rvert^2}{A_{p_r}B_{p_r}-\lvert C_r\rvert^2}\ge 0. \end{align*} $$
$$ \begin{align*}u_r'=A^{\prime}_{p_r}B_{p_r}-(\lvert C_r\rvert^2)'=\frac{3}{4}B_{p_r}+\left(\frac{9}{8}+\frac{c^2_{p_rp_r}}{2}\right)\frac{B_{p_r}\lvert C_r\rvert^2}{A_{p_r}B_{p_r}-\lvert C_r\rvert^2}\ge 0. \end{align*} $$
This guarantees
 $$ \begin{align*}A_{p_r}'=\frac{3}{4}\left(1+\frac{\lvert C_{r}\rvert^2}{A_{p_r}B_{p_r}-\lvert C_r\rvert^2}\right)\le \frac{3}{4}\left(1+\frac{K}{u_r(0)}\right), \end{align*} $$
$$ \begin{align*}A_{p_r}'=\frac{3}{4}\left(1+\frac{\lvert C_{r}\rvert^2}{A_{p_r}B_{p_r}-\lvert C_r\rvert^2}\right)\le \frac{3}{4}\left(1+\frac{K}{u_r(0)}\right), \end{align*} $$
where
![]() $K>0$
such that
$K>0$
such that
![]() $\lvert C_r\rvert ^2\le K$
, for all
$\lvert C_r\rvert ^2\le K$
, for all
![]() $ t\ge 0$
. This implies the long-time existence. As regards the last part of the statement, it is sufficient to prove that
$ t\ge 0$
. This implies the long-time existence. As regards the last part of the statement, it is sufficient to prove that
 $$ \begin{align*}\lim_{t\to+\infty} \frac{\lvert C_r\rvert^2}{u_r}=0. \end{align*} $$
$$ \begin{align*}\lim_{t\to+\infty} \frac{\lvert C_r\rvert^2}{u_r}=0. \end{align*} $$
However,
Therefore,
Then
and, since
![]() $\lvert C_r\rvert ^2$
is bounded, the assertion follows.
$\lvert C_r\rvert ^2$
is bounded, the assertion follows.
Proof of Theorem 1.1 Let
![]() $\omega $
be a left-invariant pluriclosed metric on an Oeljeklaus–Toma manifold. Corollary 5.5 implies that pluriclosed flow starting from
$\omega $
be a left-invariant pluriclosed metric on an Oeljeklaus–Toma manifold. Corollary 5.5 implies that pluriclosed flow starting from
![]() $\omega $
has a long-time solution
$\omega $
has a long-time solution
![]() $\omega _t$
such that
$\omega _t$
such that
We show that
![]() $\frac {\omega _t}{1+t}$
satisfies conditions 1–3 in Proposition 3.1. Here, we denote by
$\frac {\omega _t}{1+t}$
satisfies conditions 1–3 in Proposition 3.1. Here, we denote by
![]() $|\cdot |_t$
the norm induced by
$|\cdot |_t$
the norm induced by
![]() $\omega _t$
.
$\omega _t$
.
Taking into account that
condition 2 follows.
Thanks to the fact that condition 2 holds,
 $$ \begin{align*}\omega_{t|\mathfrak h\oplus \mathfrak h}= \sum_{i=1}^sA_i(t)\omega^i\wedge \bar \omega^i \end{align*} $$
$$ \begin{align*}\omega_{t|\mathfrak h\oplus \mathfrak h}= \sum_{i=1}^sA_i(t)\omega^i\wedge \bar \omega^i \end{align*} $$
with
![]() $\frac {A_i(t)}{1+t}\to \frac 34$
as
$\frac {A_i(t)}{1+t}\to \frac 34$
as
![]() $t\to \infty $
, and there exist
$t\to \infty $
, and there exist
![]() $C,T>0$
such that, for every vector
$C,T>0$
such that, for every vector
![]() $v\in \mathfrak h$
,
$v\in \mathfrak h$
,
for every
![]() $t\geq T$
, condition 1 is satisfied.
$t\geq T$
, condition 1 is satisfied.
In order to prove condition 3, let
![]() $\epsilon , \ell>0$
and let
$\epsilon , \ell>0$
and let
![]() $\gamma $
be a curve in M tangent to
$\gamma $
be a curve in M tangent to
![]() $\mathcal H$
which is parameterized by arclength with respect to
$\mathcal H$
which is parameterized by arclength with respect to
![]() $3\omega _\infty $
and such that
$3\omega _\infty $
and such that
![]() $L_{\infty }(\gamma )<\ell $
. Let
$L_{\infty }(\gamma )<\ell $
. Let
![]() $v=\dot \gamma $
and
$v=\dot \gamma $
and
![]() $T>0$
such that
$T>0$
such that
 $$ \begin{align*}\left\vert \frac{A_i(t)}{1+t}-\frac{3}{4}\right\vert\leq \frac{3\epsilon^2}{4\ell^2}, \end{align*} $$
$$ \begin{align*}\left\vert \frac{A_i(t)}{1+t}-\frac{3}{4}\right\vert\leq \frac{3\epsilon^2}{4\ell^2}, \end{align*} $$
for
![]() $t\ge T$
. Then
$t\ge T$
. Then
 $$ \begin{align*}\left\vert\frac{1}{1+t}|v|^2_t-|v|^2_{\infty}\right\vert\le \sum_{i=1}^{s}\left\vert\frac{A_i(t)}{1+t}-\frac34 \right\vert\lvert v_i\rvert^2\leq \frac{\epsilon^2}{\ell^2} \end{align*} $$
$$ \begin{align*}\left\vert\frac{1}{1+t}|v|^2_t-|v|^2_{\infty}\right\vert\le \sum_{i=1}^{s}\left\vert\frac{A_i(t)}{1+t}-\frac34 \right\vert\lvert v_i\rvert^2\leq \frac{\epsilon^2}{\ell^2} \end{align*} $$
and
 $$ \begin{align*}|L_{t}(\gamma)-L_{\infty}(\gamma)|\le \int_{0}^{b}\left\lvert\frac{1}{\sqrt{1+t}}|\dot \gamma |_t-|\dot \gamma|_\infty\right\rvert da\leq \frac{\epsilon}{\ell}b\leq \epsilon , \end{align*} $$
$$ \begin{align*}|L_{t}(\gamma)-L_{\infty}(\gamma)|\le \int_{0}^{b}\left\lvert\frac{1}{\sqrt{1+t}}|\dot \gamma |_t-|\dot \gamma|_\infty\right\rvert da\leq \frac{\epsilon}{\ell}b\leq \epsilon , \end{align*} $$
since
![]() $b\leq \ell $
.
$b\leq \ell $
.
Now, we show the last part of the statement, using the same argument as in Proposition 4.1, and we prove that
![]() $(\mathbb H^s\times \mathbb C^s, \frac {\omega _t}{1+t})$
converges in the Cheeger–Gromov sense to
$(\mathbb H^s\times \mathbb C^s, \frac {\omega _t}{1+t})$
converges in the Cheeger–Gromov sense to
![]() $(\mathbb H^s\times \mathbb C^s, \tilde {\omega }_{\infty })$
, where
$(\mathbb H^s\times \mathbb C^s, \tilde {\omega }_{\infty })$
, where
![]() $\tilde {\omega }_{\infty }$
is an algebraic soliton. Again, here we are identifying
$\tilde {\omega }_{\infty }$
is an algebraic soliton. Again, here we are identifying
![]() $\omega _t$
with its pullback onto
$\omega _t$
with its pullback onto
![]() $\mathbb H^s\times \mathbb C^s$
and we are fixing as base point the identity element of
$\mathbb H^s\times \mathbb C^s$
and we are fixing as base point the identity element of
![]() $\mathbb H^s\times \mathbb C^s$
. It is enough to construct a one-parameter family of biholomorphisms
$\mathbb H^s\times \mathbb C^s$
. It is enough to construct a one-parameter family of biholomorphisms
![]() $\{\varphi _t\}$
of
$\{\varphi _t\}$
of
![]() $\mathbb H^s\times \mathbb C^s$
such that
$\mathbb H^s\times \mathbb C^s$
such that
As we already observed, since
![]() $\mathfrak {I}$
is abelian, the endomorphism represented by the matrix
$\mathfrak {I}$
is abelian, the endomorphism represented by the matrix
 $$ \begin{align*}D=\begin{pmatrix} 0 & 0 \\ 0 & I_{\mathfrak{I}}\end{pmatrix} \end{align*} $$
$$ \begin{align*}D=\begin{pmatrix} 0 & 0 \\ 0 & I_{\mathfrak{I}}\end{pmatrix} \end{align*} $$
is a derivation of
![]() $\mathfrak {g}$
that commutes with the complex structure J. Then we can consider
$\mathfrak {g}$
that commutes with the complex structure J. Then we can consider
 $$ \begin{align*}d\varphi_t= \exp(s(t)D)=\begin{pmatrix}I_{\mathfrak{h}}& 0 \\ 0 & e^{s(t)}I_{\mathfrak{I}}\end{pmatrix}\in \mathrm{Aut}(\mathfrak{g}, J), \end{align*} $$
$$ \begin{align*}d\varphi_t= \exp(s(t)D)=\begin{pmatrix}I_{\mathfrak{h}}& 0 \\ 0 & e^{s(t)}I_{\mathfrak{I}}\end{pmatrix}\in \mathrm{Aut}(\mathfrak{g}, J), \end{align*} $$
where
![]() $s(t)=\log (\sqrt {1+t})$
. Using
$s(t)=\log (\sqrt {1+t})$
. Using
![]() $d\varphi _t$
, we can define
$d\varphi _t$
, we can define
For
![]() $i=1,\ldots , s$
, we have
$i=1,\ldots , s$
, we have
 $$ \begin{align*}\begin{aligned} \frac{1}{1+t}(\varphi_t^*\omega_t)(Z_i,\bar Z_i)=&\, \frac{1}{1+t}\omega_t(Z_i,\bar Z_i)\to \frac34\sqrt{-1}\, , \quad \mbox{as } t\to \infty, \\ \frac{1}{1+t}(\varphi_t^*\omega_t)(Z_i,\bar W_i)=&\, \frac{1}{\sqrt{1+t}}\omega_t(Z_i, \bar W_i )\to 0\, , \quad \mbox{as } t\to \infty, \\ \frac{1}{1+t}(\varphi_t^*\omega_t)(W_i,\bar W_i)=&\,\omega_t(W_i,\bar W_i)=\sqrt{-1}B_i(0). \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \frac{1}{1+t}(\varphi_t^*\omega_t)(Z_i,\bar Z_i)=&\, \frac{1}{1+t}\omega_t(Z_i,\bar Z_i)\to \frac34\sqrt{-1}\, , \quad \mbox{as } t\to \infty, \\ \frac{1}{1+t}(\varphi_t^*\omega_t)(Z_i,\bar W_i)=&\, \frac{1}{\sqrt{1+t}}\omega_t(Z_i, \bar W_i )\to 0\, , \quad \mbox{as } t\to \infty, \\ \frac{1}{1+t}(\varphi_t^*\omega_t)(W_i,\bar W_i)=&\,\omega_t(W_i,\bar W_i)=\sqrt{-1}B_i(0). \end{aligned} \end{align*} $$
Then
where
Notice that
![]() $\tilde {\omega }_{\infty }$
is an algebraic soliton diagonal since
$\tilde {\omega }_{\infty }$
is an algebraic soliton diagonal since
![]() $\omega _{|\mathfrak {I}\oplus \mathfrak {I}}$
is diagonal in view of Proposition 5.2.
$\omega _{|\mathfrak {I}\oplus \mathfrak {I}}$
is diagonal in view of Proposition 5.2.
6 A generalization to semidirect product of Lie algebras
From the viewpoint of Lie groups, the algebraic structure of Oeljeklaus–Toma manifolds is quite rigid and some of the results in the previous sections can be generalized to semidirect product of Lie algebras.
In this section, we consider a Lie algebra
![]() $\mathfrak {g}$
which is a semidirect product of Lie algebras
$\mathfrak {g}$
which is a semidirect product of Lie algebras
where
![]() $\lambda \colon \mathfrak h\to \mathrm {Der}(\mathfrak I)$
is a representation. We further assume that
$\lambda \colon \mathfrak h\to \mathrm {Der}(\mathfrak I)$
is a representation. We further assume that
![]() $\mathfrak {g}$
has a complex structure of the form
$\mathfrak {g}$
has a complex structure of the form
where
![]() $J_{\mathfrak h}$
and
$J_{\mathfrak h}$
and
![]() $J_{\mathfrak I}$
are complex structures on
$J_{\mathfrak I}$
are complex structures on
![]() $\mathfrak h$
and
$\mathfrak h$
and
![]() $\mathfrak I$
, respectively.
$\mathfrak I$
, respectively.
The following assumptions are all satisfied in the case of an Oeljeklaus–Toma manifold:
-
i.
 $\mathfrak h$
has
$\mathfrak h$
has
 $(1,0)$
-frame such that
$(1,0)$
-frame such that
 $\{Z_1,\dots ,Z_r\}$
such that
$\{Z_1,\dots ,Z_r\}$
such that
 $[Z_k,\bar Z_k]=\,-\frac {\sqrt {-1}}{2}(Z_k+\bar Z_k)$
, for all
$[Z_k,\bar Z_k]=\,-\frac {\sqrt {-1}}{2}(Z_k+\bar Z_k)$
, for all
 $k=1,\dots ,r$
, and the other brackets vanish.
$k=1,\dots ,r$
, and the other brackets vanish. -
ii.
 $\mathfrak I$
is a
$\mathfrak I$
is a
 $2s$
-dimensional abelian Lie algebra, and
$2s$
-dimensional abelian Lie algebra, and
 $J_{\mathfrak I}$
is a complex structure on
$J_{\mathfrak I}$
is a complex structure on
 $\mathfrak I$
.
$\mathfrak I$
. -
iii.
 $\lambda (\mathfrak h^{1,0})\subseteq \mathrm {End}(\mathfrak I)^{1,0}$
.
$\lambda (\mathfrak h^{1,0})\subseteq \mathrm {End}(\mathfrak I)^{1,0}$
. -
iv.
 $\mathfrak I$
has a
$\mathfrak I$
has a
 $(1,0)$
-frame
$(1,0)$
-frame
 $\{W_1,\dots W_s\}$
such that
$\{W_1,\dots W_s\}$
such that
 $\lambda (Z)\cdot \bar W_r=\lambda _r(Z)\bar W_r$
, for every
$\lambda (Z)\cdot \bar W_r=\lambda _r(Z)\bar W_r$
, for every
 $r=1,\dots ,s$
, where
$r=1,\dots ,s$
, where
 $\lambda _r\in \Lambda ^{1,0}(\mathfrak {h})$
.
$\lambda _r\in \Lambda ^{1,0}(\mathfrak {h})$
. -
v.
 $\sum _{a=1}^s\Im \mathfrak m(\lambda _a(Z_i))$
is constant on i.
$\sum _{a=1}^s\Im \mathfrak m(\lambda _a(Z_i))$
is constant on i. -
vi.
 $\mathfrak I$
has a
$\mathfrak I$
has a
 $(1,0)$
-frame
$(1,0)$
-frame
 $\{W_1,\dots W_s\}$
such that
$\{W_1,\dots W_s\}$
such that
 $\lambda (Z)\cdot W_r=\lambda ^{\prime }_r(Z) W_r$
, for every
$\lambda (Z)\cdot W_r=\lambda ^{\prime }_r(Z) W_r$
, for every
 $r=1,\dots ,s$
, where
$r=1,\dots ,s$
, where
 $\lambda _r'\in \Lambda ^{1,0}(\mathfrak {h})$
and
$\lambda _r'\in \Lambda ^{1,0}(\mathfrak {h})$
and
 $\sum _{a=1}^s\Im \mathfrak m(\lambda _a'(Z_i))$
is constant on i.
$\sum _{a=1}^s\Im \mathfrak m(\lambda _a'(Z_i))$
is constant on i.
Note that condition i is equivalent to require that
 $\mathfrak h=\underbrace {\mathfrak {f}\oplus \dots \oplus \mathfrak {f}}_{r\mbox {-times}}$
equipped with the complex structure
$\mathfrak h=\underbrace {\mathfrak {f}\oplus \dots \oplus \mathfrak {f}}_{r\mbox {-times}}$
equipped with the complex structure
 $J_{\mathfrak {h}}=\underbrace {J_{\mathfrak f}\oplus \dots \oplus J_{\mathfrak f}}_{r\mbox {-times}}$
, whereas in condition iv, the existence of
$J_{\mathfrak {h}}=\underbrace {J_{\mathfrak f}\oplus \dots \oplus J_{\mathfrak f}}_{r\mbox {-times}}$
, whereas in condition iv, the existence of
![]() $\{W_r\}$
and
$\{W_r\}$
and
![]() $\lambda _r$
is equivalent to require that
$\lambda _r$
is equivalent to require that
for every
![]() $Z,Z'\in \mathfrak h^{1,0}$
.
$Z,Z'\in \mathfrak h^{1,0}$
.
The computations in Section 5 can be used to study solutions to the flow
in semidirect products of Lie algebras (this flow coincides with the pluriclosed flow only when the initial metric is pluriclosed). We have the following proposition.
Proposition 6.1 Let
![]() $\mathfrak g=\mathfrak h \ltimes _{\lambda } \mathfrak I$
be a semidirect product of Lie algebras equipped with a splitting complex structure
$\mathfrak g=\mathfrak h \ltimes _{\lambda } \mathfrak I$
be a semidirect product of Lie algebras equipped with a splitting complex structure
![]() $J=J_{\mathfrak h}\oplus J_{\mathfrak I}$
, and let
$J=J_{\mathfrak h}\oplus J_{\mathfrak I}$
, and let
![]() $\omega $
be a Hermitian metric on
$\omega $
be a Hermitian metric on
![]() $\mathfrak {g}$
making
$\mathfrak {g}$
making
![]() $\mathfrak h$
and
$\mathfrak h$
and
![]() $\mathfrak I$
orthogonal. Then the Bismut–Ricci form of
$\mathfrak I$
orthogonal. Then the Bismut–Ricci form of
![]() $\omega $
satisfies
$\omega $
satisfies
![]() $\rho ^{1,1} _{B|\mathfrak h\oplus \mathfrak I}=\rho ^{1,1} _{B|\mathfrak I\oplus \mathfrak I}=0.$
$\rho ^{1,1} _{B|\mathfrak h\oplus \mathfrak I}=\rho ^{1,1} _{B|\mathfrak I\oplus \mathfrak I}=0.$
If conditions
![]() $\mathrm {i}$
–
$\mathrm {i}$
–
![]() $\mathrm {iv}$
hold and
$\mathrm {iv}$
hold and
![]() $\omega _{|\mathfrak h\oplus \mathfrak h}$
is diagonal with respect to the frame
$\omega _{|\mathfrak h\oplus \mathfrak h}$
is diagonal with respect to the frame
![]() $\{Z_i\}$
, then the
$\{Z_i\}$
, then the
![]() $(1,1)$
-component of the Bismut–Ricci form of
$(1,1)$
-component of the Bismut–Ricci form of
![]() $\omega $
does not depend on
$\omega $
does not depend on
![]() $\omega $
and the solution to the flow (27) starting from
$\omega $
and the solution to the flow (27) starting from
![]() $\omega $
takes the following expression:
$\omega $
takes the following expression:
If conditions
![]() $\mathrm {i}$
–
$\mathrm {i}$
–
![]() $\mathrm {iv}$
and
$\mathrm {iv}$
and
![]() $\mathrm {vi}$
hold and
$\mathrm {vi}$
hold and
![]() $\omega _{|\mathfrak h\oplus \mathfrak h}$
is a multiple of the canonical metric with respect to the frame
$\omega _{|\mathfrak h\oplus \mathfrak h}$
is a multiple of the canonical metric with respect to the frame
![]() $\{Z_i\}$
, then
$\{Z_i\}$
, then
![]() $\omega $
is a soliton for flow (27) with cosmological constant
$\omega $
is a soliton for flow (27) with cosmological constant
![]() $c=\frac {1}{2}+\sum _{a=1}^s\Im \mathfrak m(\lambda _a'(Z_i))$
.
$c=\frac {1}{2}+\sum _{a=1}^s\Im \mathfrak m(\lambda _a'(Z_i))$
.
The previous proposition does not cover the case when properties i–iv are satisfied and the restriction to
![]() $\mathfrak h\oplus \mathfrak h$
of the initial Hermitian inner product
$\mathfrak h\oplus \mathfrak h$
of the initial Hermitian inner product
 $$ \begin{align*}\omega=\sqrt{-1}\sum _{a,b=1}^r g_{a\bar b}\omega^a\wedge \bar \omega^b+\sqrt{-1}\sum _{a,b=1}^s g_{r+a\overline{r+ b}}\gamma^a\wedge \bar \gamma^b \end{align*} $$
$$ \begin{align*}\omega=\sqrt{-1}\sum _{a,b=1}^r g_{a\bar b}\omega^a\wedge \bar \omega^b+\sqrt{-1}\sum _{a,b=1}^s g_{r+a\overline{r+ b}}\gamma^a\wedge \bar \gamma^b \end{align*} $$
is not diagonal with respect to
![]() $\{Z_i\}$
. In this case flow (27) evolves only the components
$\{Z_i\}$
. In this case flow (27) evolves only the components
![]() $g_{i\bar i}$
of
$g_{i\bar i}$
of
![]() $\omega $
along
$\omega $
along
![]() $\omega ^i\wedge \bar \omega ^i$
via the ODE
$\omega ^i\wedge \bar \omega ^i$
via the ODE
 $$ \begin{align*}\partial_{t}g_{i\bar i}=\frac14 \sum_{a=1}^r g^{\bar a a}\Re \mathfrak{e}\,g_{i\bar a} -\frac12 \sum_{c,d=1}^s g^{\overline{r+d} r+ c} \left\lbrace \omega([Z_i,W_c],\bar W_d) + \omega([\bar Z_i,\bar W_c],W_d) \right\rbrace, \end{align*} $$
$$ \begin{align*}\partial_{t}g_{i\bar i}=\frac14 \sum_{a=1}^r g^{\bar a a}\Re \mathfrak{e}\,g_{i\bar a} -\frac12 \sum_{c,d=1}^s g^{\overline{r+d} r+ c} \left\lbrace \omega([Z_i,W_c],\bar W_d) + \omega([\bar Z_i,\bar W_c],W_d) \right\rbrace, \end{align*} $$
where
![]() $g_{i\bar i}$
depends on t. Note that the quantities
$g_{i\bar i}$
depends on t. Note that the quantities
![]() $-\frac 12 \sum _{c,d=1}^s g^{\overline {r+d} r+ c} \left \lbrace \omega ([Z_i,W_c], \bar W_d) + \omega ([\bar Z_i,\bar W_c],W_d) \right \rbrace $
appearing in the evolution of
$-\frac 12 \sum _{c,d=1}^s g^{\overline {r+d} r+ c} \left \lbrace \omega ([Z_i,W_c], \bar W_d) + \omega ([\bar Z_i,\bar W_c],W_d) \right \rbrace $
appearing in the evolution of
![]() $g_{i\bar i}$
are independent on t.
$g_{i\bar i}$
are independent on t.
The same computations as in Section 4 imply the following proposition.
Proposition 6.2 Let
![]() $\mathfrak g=\mathfrak h \ltimes _{\lambda } \mathfrak I$
be a semidirect product of Lie algebras equipped with a splitting complex structure
$\mathfrak g=\mathfrak h \ltimes _{\lambda } \mathfrak I$
be a semidirect product of Lie algebras equipped with a splitting complex structure
![]() $J=J_{\mathfrak h}\oplus J_{\mathfrak I}$
. Assume that properties
$J=J_{\mathfrak h}\oplus J_{\mathfrak I}$
. Assume that properties
![]() $\mathrm {i}$
–
$\mathrm {i}$
–
![]() $\mathrm {iii}$
are satisfied, and let
$\mathrm {iii}$
are satisfied, and let
![]() $\omega $
be a left-invariant Hermitian metric on
$\omega $
be a left-invariant Hermitian metric on
![]() $\mathfrak {g}$
. Then
$\mathfrak {g}$
. Then
whereas
![]() $ \rho _{C |\mathfrak h\oplus \mathfrak h}$
is diagonal with respect to
$ \rho _{C |\mathfrak h\oplus \mathfrak h}$
is diagonal with respect to
![]() $\{Z_1,\ldots , Z_r\}$
.
$\{Z_1,\ldots , Z_r\}$
.
If, in addition, property
![]() $\mathrm {iv}$
holds, then
$\mathrm {iv}$
holds, then
 $$ \begin{align*}\rho_C(Z_i,\bar Z_i)=-\sqrt{-1}\left(\frac12-\sum_{a=1}^s\Im\mathfrak m(\lambda_{a}(Z_i))\right), \quad \mbox{for all } i=1,\ldots, r. \end{align*} $$
$$ \begin{align*}\rho_C(Z_i,\bar Z_i)=-\sqrt{-1}\left(\frac12-\sum_{a=1}^s\Im\mathfrak m(\lambda_{a}(Z_i))\right), \quad \mbox{for all } i=1,\ldots, r. \end{align*} $$
If, in addition, property
![]() $\mathrm {v}$
holds, then
$\mathrm {v}$
holds, then
![]() $\omega $
is a soliton for the Chern–Ricci flow with cosmological constant
$\omega $
is a soliton for the Chern–Ricci flow with cosmological constant
![]() $c=\frac {1}{2}-\sum _{a=1}^s\Im \mathfrak m(\lambda _a(Z_i))$
if and only if
$c=\frac {1}{2}-\sum _{a=1}^s\Im \mathfrak m(\lambda _a(Z_i))$
if and only if
![]() $\omega _{\mathfrak {h}\oplus \mathfrak h}$
is a multiple of the canonical metric on
$\omega _{\mathfrak {h}\oplus \mathfrak h}$
is a multiple of the canonical metric on
![]() $\mathfrak h $
with respect to the frame
$\mathfrak h $
with respect to the frame
![]() $\{Z_i\}$
and
$\{Z_i\}$
and
![]() $\omega _{\mathfrak h\oplus \mathfrak J }=0$
.
$\omega _{\mathfrak h\oplus \mathfrak J }=0$
.
Acknowledgment
We are grateful to Daniele Angella, Ramiro Lafuente, Francesco Pediconi, and Alberto Raffero for useful conversations. In particular, Ramiro Lafuente suggested us how to prove the convergence in the Cheeger–Gromov sense in Theorem 1.1.