Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sourour, A.R
1981.
Isometries of norm ideals of compact operators.
Journal of Functional Analysis,
Vol. 43,
Issue. 1,
p.
69.
Magajna, Bojan
1985.
On subnormality of generalized derivations and tensor products.
Bulletin of the Australian Mathematical Society,
Vol. 31,
Issue. 2,
p.
235.
Synnatzschke, J.
1985.
Über eindimensionale Elemente linearer Algebren und einige algebraische Eigenschaften eines elementaren Operators.
Mathematische Nachrichten,
Vol. 123,
Issue. 1,
p.
121.
Gravner, Janko
1986.
A note on elementary operators on the Calkin algebra.
Proceedings of the American Mathematical Society,
Vol. 97,
Issue. 1,
p.
79.
Magajna, Bojan
1987.
On the essential numerical range of a generalized derivation.
Proceedings of the American Mathematical Society,
Vol. 99,
Issue. 1,
p.
86.
Mathieu, Martin
1988.
Elementary operators on prime C*-algebras II.
Glasgow Mathematical Journal,
Vol. 30,
Issue. 3,
p.
275.
Mathieu, Martin
1989.
Elementary operators on primeC *-algebras. I.
Mathematische Annalen,
Vol. 284,
Issue. 2,
p.
223.
Hladnik, Milan
1990.
Spectrality of elementary operators.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 49,
Issue. 2,
p.
327.
Hou, Jinchuan
1991.
On operator inequalities and linear combinations of operators.
Linear Algebra and its Applications,
Vol. 153,
Issue. ,
p.
35.
Magajna, Bojan
1991.
On the relative reflexivity of finitely generated modules of operators.
Transactions of the American Mathematical Society,
Vol. 327,
Issue. 1,
p.
221.
Bresar, Matej
1991.
On the distance of the composition of two derivations to the generalized derivations.
Glasgow Mathematical Journal,
Vol. 33,
Issue. 1,
p.
89.
Magajna, Bojan
1993.
A transitivity theorem for algebras of elementary operators.
Proceedings of the American Mathematical Society,
Vol. 118,
Issue. 1,
p.
119.
Coates, Keith J.
1994.
Algebraic Methods in Operator Theory.
p.
49.
Ara, Pere
and
Mathieu, Martin
1994.
On the central Haagerup tensor product.
Proceedings of the Edinburgh Mathematical Society,
Vol. 37,
Issue. 1,
p.
161.
Lu, Shijie
and
Lu, Fangyan
1995.
Normality preserving multiplication operators.
Acta Mathematica Sinica,
Vol. 11,
Issue. 4,
p.
389.
Sukochev, F. A.
1996.
Isometries of symmetric operator spaces associated with AFD factors of typeII and symmetric vector-valued spaces.
Integral Equations and Operator Theory,
Vol. 26,
Issue. 1,
p.
102.
Brešar, M.
and
Šemrl, P.
1999.
Elementary operators.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 129,
Issue. 6,
p.
1115.
Saksman, Eero
and
Tylli, Hans-Olav
1999.
The Apostol–Fialkow Formula for Elementary Operators on Banach Spaces.
Journal of Functional Analysis,
Vol. 161,
Issue. 1,
p.
1.
Barraa, Mohamed
and
Pedersen, Steen
1999.
On the product of two generalized derivations.
Proceedings of the American Mathematical Society,
Vol. 127,
Issue. 9,
p.
2679.
Duggal, B.P
2001.
The Commutant Modulo Cp of Co-prime Powers of Operators on a Hilbert Space.
Journal of Mathematical Analysis and Applications,
Vol. 263,
Issue. 1,
p.
110.
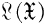 , the algebra of bounded operators on ᚕ, defined by
, the algebra of bounded operators on ᚕ, defined by