Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T00:50:18.376Z Has data issue: false hasContentIssue false
  • English
  • Français

On Strong Nörlund Summability Fields

Published online by Cambridge University Press:  20 November 2018

Brian Kuttner  and
Brian Thorpe
Brian Kuttner
Affiliation:
University of Birmingham, Birmingham, England
Brian Thorpe
Affiliation:
University of Western Ontario, London, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let p denote the sequence {pn} and set 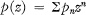wherever this series converges. (Where no limits are stated, sums are throughout to be taken from n = 0 to n = ∞.) We use a similar notation with other letters in place of p. Given two sequences p, q, the convolution p*q is defined by

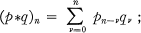
it is familiar, and easily verified, that the operation of convolution is commutative and associative. We write Pn = (p*l)n (where 1 denotes the sequence {1} ), and take P-1 to mean 0. If, for all n ≦ 0, Pn ≠ 0, then we define the Nörlund mean (N, p) of the sequence s as σn, where

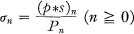
and (σ-1 = 0. If σn → λ as n → ∞, then 5 is said to be limitable (N, p) to the number λ

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 24 , Issue 3 , June 1972 , pp. 390 - 399
Copyright
Copyright © Canadian Mathematical Society 1972

References

1. Borwein, D. and Cass, F. P., Strong Nörland summability, Math. Z. 103 (1968), 94–111.Google Scholar
2. Hardy, G. H., Divergent series (Oxford University Press, London, 1949).Google Scholar
3. Kuttner, B. and Thorpe, B., On the strong Nörlund summability of a Cauchy product series, Math. Z. 111 (1969), 69–86.Google Scholar
4. Kwee, B., Some theorems on Nörlund summabiiity, Proc. London Math. Soc. 14, (1964), 353–368.Google Scholar
5. Mears, F. M., Absolute regularity and the Nörlund mean, Ann. of Math. 38 (1937), 594–601.Google Scholar
6. Miesner, W., The convergence fields of Nörlund means, Proc. London Math. Soc. 15 (1965), 495–507.Google Scholar
7. Peyerimhoff, A., On convergence fields of Nörlund means, Proc. Amer. Math. Soc. 7 (1956), 335–347.Google Scholar
8. Zygmund, A., Trigometric series (Cambridge University Press, London, 1959).Google Scholar