Hostname: page-component-f554764f5-fr72s Total loading time: 0 Render date: 2025-04-10T13:24:31.185Z Has data issue: false hasContentIssue false
  • English
  • Français

On Multiplicative Properties of Families of Complexes of Certain Loops

Published online by Cambridge University Press:  20 November 2018

Meir Steinberger
Meir Steinberger*
Affiliation:
University of Haifa, Haifa, Israel
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is well-known that if 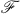is a quotient group of a group G, then (i) 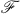is a partition of G, and (ii) the usual complex product (in the usual sense of multiplication of complexes) of every pair of members of 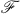is a member of 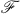. There arises the question whether, conversely, (i) and (ii), perhaps in a weaker form, suffice for 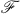to be a quotient group of G.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 25 , Issue 5 , October 1973 , pp. 1066 - 1077
Copyright
Copyright © Canadian Mathematical Society 1973

References

1. Artzy, R., Crossed inverse and related loops, Trans. Amer. Math. Soc. 91 (1959), 480–492.Google Scholar
2. Bates, G. E. and Kiokemeister, K., A note on homomorphic mappings of quasigroups into multiplicative systems, Bull. Amer. Math. Soc. 54 (1948), 1180–1185.Google Scholar
3. Bruck, R. H., A survey of binary systems (Springer Verlag, Berlin, 1958).Google Scholar
4. Ginzburg, A., Systèmes multiplicatifs de relations. Boucles quasi-associatives, C. R. Acad. Sci. Paris Sér. A-B 250 (1960), 1413–1416.Google Scholar
5. Huthnance, E. D., A theory of generalized Moufang loops, Ph.D. Thesis, Georgia Institute of Technology, 1968.Google Scholar
6. Osborn, J. M., Loops with the weak inverse property, Pacific J. Math. 10 (1960), 295–304.Google Scholar
7. Robinson, D. A., Bol loops, Trans, Amer. Math. Soc. 123 (1966), 341–354.Google Scholar
8. Zassenhaus, H. J., The theory of groups, 2nd ed. (Chelsea Publ. Co., New York, 1958).Google Scholar