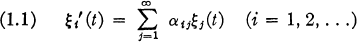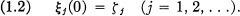Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Marinov, Corneliu
1984.
Qualitative properties of lp-solutions of infinite differential systems via dissipativity.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 8,
Issue. 5,
p.
441.
Kloeden, Peter E.
and
Lorenz, Thomas
2025.
The Exponential of the Lattice Laplacian Operator and the Mean-Square Attractor of A Stochastic Lattice System.
Journal of Dynamics and Differential Equations,