Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T13:51:08.124Z Has data issue: false hasContentIssue false
  • English
  • Français

On Hessian Limit Directions along Gradient Trajectories

Published online by Cambridge University Press:  20 November 2018

Vincent Grandjean
Vincent Grandjean*
Affiliation:
Departamento de Matemática, UFC, Av. Humberto Monte s/n, Campus do Pici Bloco 914, CEP 60.455-760, Fortaleza-CE, Brasil, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a non-oscillating gradient trajectory 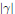$\left| \text{ }\!\!\gamma\!\!\text{ } \right|$ of a real analytic function $f$, we show that the limit 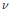$v$ of the secants at the limit point 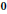$0$ of 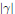$\left| \text{ }\!\!\gamma\!\!\text{ } \right|$ along the trajectory 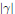$\left| \text{ }\!\!\gamma\!\!\text{ } \right|$ is an eigenvector of the limit of the direction of the Hessian matrix Hess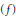$\left( f \right)$ at 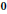$0$ along 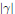$\left| \text{ }\!\!\gamma\!\!\text{ } \right|$. The same holds true at infinity if the function is globally sub-analytic. We also deduce some interesting estimates along the trajectory. Away from the ends of the ambient space, this property is of metric nature and still holds in a general Riemannian analytic setting.

Keywords

34A2634C0832Bxx32Sxxgradient trajectoriesnon-oscillationlimit of Hessian directionsimit of secantstrajectories at infinity
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 4 , 01 August 2013 , pp. 808 - 822
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Cano, F.,Moussu, R., and Rolin, J-P., Non-oscillating integral curves and valuations. J. Reine Angew. Math. 582(2005), 107–141. http://dx.doi.org/10.1515/crll.2005.2005.582.107 Google Scholar
[2] Cano, F., Moussu, R., and Sanz, F., Oscillation, spiralement, tourbillonnement. Comm. Math. Helv. 75(2000), no. 2, 284–318. http://dx.doi.org/10.1007/s000140050127 Google Scholar
[3] D’Acunto, D. and Grandjean, V., On gradient at infinity of semi-algebraic functions. Ann. Pol. Math. 87(2005), 39–49. http://dx.doi.org/10.4064/ap87-0-4 Google Scholar
[4] D’Acunto, D., On gradient inequality at infinity of tame functions. Rev. Mat. Complut. 18(2005), no. 2, 493–501.Google Scholar
[5] Fortuny, P. and Sanz, F., Gradient vector fields do not generate twister dynamics. J. Differential Equations 174(2001), no. 1, 91–100. http://dx.doi.org/10.1006/jdeq.2000.3926 Google Scholar
[6] Grandjean, V., On the limit set at infinity of a gradient of semi-algebraic functions. J. Differential Equations 233(2007), no. 1, 22–41. http://dx.doi.org/10.1016/j.jde.2006.10.009 Google Scholar
[7] Grandjean, V., Gradient trajectories for plane singular metrics I: oscillating trajectories. arxiv:1205.6749 Google Scholar
[8] Grandjean, V. and Sanz, F., On restricted analytic gradient on analytic isolated surface singularities. arxiv:1105.3888 Google Scholar
[9] Kurdyka, K., Mostowski, T., and Parusiński, A., Proof of the gradient conjecture of R. Thom. Ann. of Math. 152(2000), no. 3, 763–792. http://dx.doi.org/10.2307/2661354 Google Scholar
[10] Kurdyka, K. and Parusiński, A., Quasi-convex decomposition in o-minimal structures. Applications to the gradient conjecture. In: Singularity theory and its applications, Adv. Stud. Pure Math., 43, Math. Soc. Japan, Tokyo, 2006, pp. 137–177.Google Scholar
[11] Kurdyka, K. and Paunescu, L., Hyperbolic polynomials and multiparameter real-analytic perturbation theory. Duke Math. J. 141(2008), no. 1, 123–149. http://dx.doi.org/10.1215/S0012-7094-08-14113-4 Google Scholar
[12] Lojasiewicz, S., Sur les trajectoires du gradient d’une fonction analytique. Seminari di Geometria 1982–1983 (Bologna 1982/1983), Univ. Stud. Bologna, Bologna, 1984, 115–117.Google Scholar
[13] Moussu, R., Sur la dynamique des gradients. Existence de variátás invariantes. Math. Ann. 307(1997), no. 3, 445–460. http://dx.doi.org/10.1007/s002080050043 Google Scholar
[14] Rolin, J.-P., Sanz, F., and Schäfke, R., Quasi-analytic solutions of analytic ordinary differential equations and o-minimal structures. Proc. Lond. Math. Soc. (3) 95(2007), no. 2, 413–442. http://dx.doi.org/10.1112/plms/pdm016 Google Scholar
[15] Sanz, F., Non-oscillating solutions of analytic gradient vector fields. Ann. Inst. Fourier (Grenoble) 48(1998), no. 4, 1045–1067. http://dx.doi.org/10.5802/aif.1648 Google Scholar
[16] Dries, L. van den, Tame topology and o-minimal structures. London Mathematical Society, Lecture Notes Series, 248, Cambridge University Press, Cambridge, 1998.Google Scholar