Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-25T17:49:06.620Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Theorem of Cohen and Lyndon About Free Bases for Normal Subgroups

Published online by Cambridge University Press:  20 November 2018

A. Karrass  and
D. Solitar
A. Karrass
Affiliation:
York University, Downsview, Ontario
D. Solitar
Affiliation:
York University, Downsview, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let S(≠1) be a subgroup of a group G. We consider the question: when are the conjugates of S “as independent as possible“? Specifically, suppose SG (the normal subgroup generated by S in G) is the free product II*S0α where 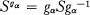and gα ranges over a subset J of G. Then J must be part of a (left) coset representative system for G mod SG. N where N is the normalizer of S in G. (For, g ∊ SGgαN implies Sg is conjugate to Sgα in SG; however, distinct non-trivial free factors of a free product are never conjugate.)

We say that SG is the free product of maximally many conjugates of S in G if SG = II*Sgα where gα ranges over a (complete) left coset representative system for G mod SGN (or equivalently, gα ranges over a double coset representative system for G mod (SG, N)); in this case we say briefly that S has the fpmmc property in G.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 24 , Issue 6 , December 1972 , pp. 1086 - 1091
Copyright
Copyright © Canadian Mathematical Society 1972

References

1. Baumslag, G., Residually finite one-relator groups, Bull. Amer. Math. Soc. 73 (1967), 618–620.Google Scholar
2. Cohen, D. E. and Lyndon, R. C., Free bases for normal subgroups of free groups, Trans. Amer. Math. Soc. 108 (1963), 526–537.Google Scholar
3. Karrass, A. and Solitar, D., The subgroups of a free product of two groups with an amalgamated subgroup, Trans. Amer. Math. Soc. 150 (1970), 227–255.Google Scholar
4. Karrass, A. and Solitar, D., Subgroups of HNN groups and groups with one defining relation, Can. J. Math. 23 (1971), 627–643.Google Scholar
5. Magnus, W., Karrass, A., and Solitar, D., Combinatorial group theory, Pure and Appl. Math., Vol. 13 (Interscience, New York 1966).Google Scholar